基于等效旋转调制的地磁提取*

杨金显, 王亚平, 王蒙蒙

(河南理工大学 电气工程与自动化学院导航制导实验室,河南 焦作 454000)

0 引 言

随着水平井、多分支井等定向井的出现,磁方位的精度直接影响钻井风险、钻遇率和井眼轨迹的调整,随钻测量(measurement while drilling,MWD)中方位精度的需求越来越高,因此需要精确地对地磁数据提取[1]。目前MWD是通过加速度计和磁强计测量的重力信息和地磁场信息获得方位角信息,其中加速度计校正方法比较成熟可靠[2]；但磁强计测量的地磁数据易受外界磁干扰和自身误差而影响方位角测量精度。陀螺仪不受周围环境磁干扰影响,但存在长时间漂移的累积误差[3]。

椭球拟合方法是地磁提取中的经典方法,其具有操作简单,不依赖外部信息,仅使用磁强计测点对地磁参数提取,但当测量设备的位置和外部磁干扰发生变化时,提取的精度降低[4,5]。文献[6]在椭球模型的基础上提出最大似然估计的方法对地磁提取参数求取。文献[7]提出使用递推最小二乘法求取补偿参数,当磁干扰变化时,递推最小二乘法求取地磁提取参数需要较长收敛时间且容易发散。外部信息,如航向角[8]、重力加速度[9]、角速度[10]等辅助地磁提取的方法也倍受关注。文献[11]提出了加速度计和磁强计的组合标定方法,方法依据在重力向量与地磁向量的交角是常值的原理，当井斜角大于或小于45°时,标定的误差会逐渐增大。相关学者提出使用更加精确的地磁提取模型的方法,如扩展卡尔曼滤波(extended Kalman filtering,EKF)[12]、容积卡尔曼滤波(cubature Kalman filtering,CKF),粒子滤波[13]、神经网络[14]等方法进地磁提取。文献[13]使用粒子群优化算法进行地磁提取,KF求取补偿参数的方法是将参数求取的问题转换成状态估计的问题。文献[15]使用CKF对地磁补偿参数提取，核心是以球形半径规则的容积变换(cubature transform,CT)，CKF中粒子点是根据协方差进行容积变换生成的,所以，粒子点与实际测点会存在一定的误差。

本文设计了一种等效旋转MWD的方案,利用泥浆流驱动的涡轮机使轴动的MWD系统旋转。以一定时间的向心加速度作为参考值,利用连续测量的向心加速度的二阶原点距判断旋转系统的稳定性,待稳定后采集大量有效的地磁测量点用于参数求取。根据采样周期与解算周期的间隔比,充分利用测量系统高速采样的特点,设计了基于多测量粒子统计信息的统计卡尔曼滤波(statistical Kalman filtering,SKF)方法对常值误差参数和动态误差参数进行估计。

1 等效旋转方案设计

在航海、航空和航天领域,旋转惯性系统需要专用的旋转机构,但是在钻井环境中,受到体积和抗冲击性等限制,采用电机驱动的旋转机构的方法不可行。因此,本文设计了一种泥浆流驱动的旋转MWD系统,其安装示意图如图1所示。

图1 等效旋转方案设计

图2为旋转MWD样机设备的旋转机构。在钻进的过程中,泥浆流会驱动涡轮机旋转,涡轮机驱动轴承转动,轴承连接着MWD系统的轴带动测量系统旋转。

图2 旋转MWD的旋转机构

由于泥浆流存在不稳定,也即驱动的旋转速度可能不稳定。为了准确估计误差参数,采用x轴或y轴的向心加速度来判断旋转是否稳定；当向心加速度或其变化率在一定时间内处于误差范围内的稳定状态时,认为旋转MWD系统可以稳定测量。因此,将某时刻的向心加速度作为基准值,设为ax0和az0,与后续的向心加速度求取二阶原点矩作为误差判定标准

式中δx,δy为允许的误差范围,可通过先验信息获得。当向心加速度的二阶原点矩在误差范围内时,该时刻的测量值可被使用,即可形成等效旋转调制过程。

2 地磁误差参数推导

2.1 地磁向量误差模型

地磁向量的测量受到多种因素的影响,大体可以分为磁效应误差和器件误差。综合多种不同的误差源,地磁误差模型可以表示为

ms=CscalCnon(Csoftmb+bhi)+bio+es=Cmb+b+eε

(2)

其中

C=CscalCnonCsoft,b=CscalCnonbhi+bio

(3)

式(2)、式(3)中ms为磁强计输出的三维地磁向量,mb为在钻具载坐标系下的地磁向量的真实值,Csoft和bhi分别为软磁效应误差矩阵和硬磁效应误差向量,Cnon为非正交误差矩阵,Cscal为比例因子误差矩阵,bio为偏置误差,es为磁强计的测量噪声。将式(3)中的参数C称为动态环境误差参数矩阵,参数b称为常值误差参数向量。

将式(2)转换至传感器坐标系下表示

mb=L(ms-b-eε)

(4)

其中,L=C-1。

2.2 误差参数的推导

在载体坐标系下,第k-1时刻和第k时刻地磁向量存在如下关系

由第k-1时刻和k时刻的测量关系可得如下方程组

对方程组(8)求解,解得向量b为

将式(8)代入式(4)中,可得待求取参数只有L的表达式

测量中,停止钻进的状态称为零速状态。在此状态下,通过椭球拟合方法求取地磁提取参数作为初值x0=[Ut(L0),b0],其中Ut(L)表示由L矩阵的上三角矩阵形成的列向量。

3.1 系统方程的构建

根据对地磁向量的常值误差参数和动态误差参数的推导,根据式(8)和式(9)建立误差参数的状态空间表达式。

1)状态转移模型

地磁向量误差补偿的非线性状态转移模型可表示为

Lk=Lk-1

(11)

2)量测模型

由于从k-1和k时刻钻进距离较小,可认为地磁模值不变,根据定点地磁模值不变的特性可得磁强计的量测模型为

y=mbTmb=[L(ms-b-eε)]TL(ms-b-eε)

(13)

将式(13)展开可得

mbTmb=h1(x)+h2(x)

(14)

式中h1(x)为量测量的模值项,h2(x)为量测量的噪声项

h1(x)=msTLTLms-2msTLTLb+bTLTLb

(15)

式(13)～式(16)可简化地将量测方程表示为

考虑实际系统的高速采样的特点,在k-1和k时刻的姿态解算间隔内可获得大量的测量数据,因此,利用多测点数据的统计特征对测量点进行融合处理,进而估计出提取参数,这种利用统计信息的滤波方式为统计卡尔曼滤波。

1)粒子点的获取

卡尔曼滤波器进行一次时间更新和量测更新,可得到当前时刻的最优估计,假设卡尔曼滤波的计算周期为Tcal,磁强计的采样周期为Tsamp,则一个计算周期中的采样粒子数

n=Tcal/Tsamp=fsamp/fcal

(18)

粒子点的获取方法:在第k个计算周期中,磁强计会测得n个地磁向量的数据点。

结合粒子的协方差,粒子点的权系数有如下约束关系

粒子点的权系数由式(19)得到

2) 时间更新过程

根据粒子点的权系数合并粒子点得到第k步计算时间更新先验估计和状态协方差矩阵

3)量测更新过程

结合量测量粒子的权系数和协方差矩阵,合并粒子点可得到第k步的量测预测值和量测协方差矩阵为

4)卡尔曼滤波估计的过程

4 实验与分析

使用本团队自主研发的磁惯性MWD模块进行实验。实验地区的地理条件为北纬35.23°,东经113.21°,磁倾角为53.93°,地磁强度为52.650 μT,地球重力加速度9.8 m/s2。实验场地选在周围没有建筑物的露天场地,以最大化的减少除实验中模拟的磁干扰外的干扰源。

4.1 模拟物理实验

1)将MWD短节固定在无磁卡座上,可在卡座内旋转;2)采用铁制螺钉作为磁干扰源,不规则的分布在测量短节周围,模拟钻井过程中环境不规则的磁干扰,如图3所示;3)使测量短节在测量过程中旋转运动,采用椭球拟合算法和本文提出的算法获得提取参数,如表1所示,并分析地磁向量提取前后模值。

图3 模拟磁干扰实验

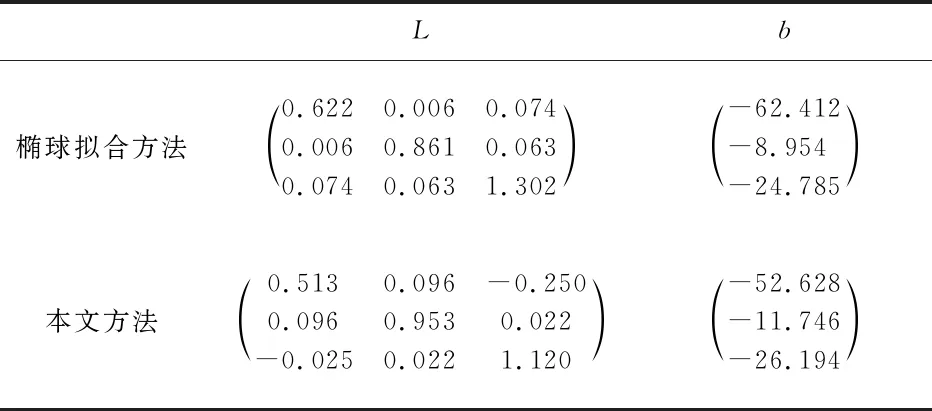
表1 模拟磁干扰实验中提取参数对比

由图4可知,由于环境中的地磁干扰不均匀分布,当测量模块转动过程中,尽管地磁测量向量经过椭球拟合算法提取,但仍有明显的振荡,说明在这种情况下椭球拟合算法失效。而本文算法能够使提取后的地磁向量模值稳定的收敛于当地地磁模值。经过本文算法求取的磁向量模值与当地地磁模值误差为0.5 μT。

图4 模拟物理实验中地磁向量模值

4.2 等效旋转钻进实验

1)把磁惯性MWD核心模块固定在某小型钻机的钻杆上,使其随钻杆一起旋转,如图5所示。2)先启动钻机处于稳定转速状态,满足式(1)的要求。3)按照图5所示的方法,进行实际钻进并无线蓝牙接收数据。对测量数据使用椭球拟合算法和本文算法进行对地磁进行提取,并求出提取参数。分析补偿前后的地磁模值和方位角误差。

图5 模拟等效旋转实验

表2为模拟旋转钻进实验中椭球拟合算法和本文算法提取的地磁向量提取误差参数。

表2 模拟钻进实验提取参数

将表2中的提取参数与地磁测点数据代入式(7)中可得提取后的地磁向量模值,如图6所示。

图6 等效旋转钻进实验中地磁向量模值

图6中未补偿的地磁向量由于存在较大的磁干扰,地磁向量的模值表现出大幅值的周期振荡。存在着地磁模值的分段的改变,说明环境中的磁干扰发生变化。椭球拟合算法处理后的地磁向量的模值的振荡幅度有一定缩小,但是仍表现为±6 μT的幅值振荡,并且在磁干扰发生变化时,模值发生不规则变化。经过本文算法处理后的地磁向量的模值稳定地收敛于当地地磁模值(52.65 μT),地磁提取效果很好。经过本文算法处理的地磁向量模值与当地地磁模值的误差为±0.75 μT。

4.3 方位角绝对误差分析

图7为两种方法提取的地磁向量解算的方位角的绝对误差对比图。方位角绝对误差是指计算方位角与参考方位角的差的绝对值,用绝对值能够准确的表示出误差的程度。

图7 方位角绝对误差

从图7可知,本文算法与椭球拟合算法相比,椭球拟合算法校正后的方位角绝对误差平均值为4.88°,本文算法方位角绝对误差降低至0.45°。

5 结 论

MWD环境中,当外界磁干扰环境发生变化时,如地质层变化,地磁提取参数需要及时的进行调整。针对该问题,基于等效旋转调制的地磁提取算法被提出,并设计了旋转MWD系统,在钻进过程中采集有效的磁场信息。根据多测点的统计信息设计了统计卡尔曼滤波器,对地磁提取参数进行估计。通过自主研发的磁惯性测量模块进行实验,实验表明：基于等效旋转调制的地磁提取算法有效的将方位角的绝对误差由提取前的4.88°降低至0.45°。