粘接胶粘弹性对加速度计热应力的影响研究

丁 姝， 黄丽斌

(东南大学 仪器科学与工程学院，江苏 南京 210096)

0 引 言

微机电系统(micro-electro-mechanical system,MEMS)器件需要为其封装提供一个相对高真空的环境以降低机械噪声的干扰，固定芯片以保证在振动冲击下芯片的可靠性，但不同材料组成的多层封装结构带来的封装效应，即由封装结构失配引入的结构变形和应力，对器件性能也会产生影响[1]。硅微谐振式加速度计是通过谐振器将惯性力测量转换为频率测量的传感器，其核心结构是一个对力敏感的双端固定音叉谐振器，受封装效应影响会导致零位温漂、标度因数温漂以及零偏稳定性的降低。在复杂封装效应中，贴片环节引起的结构热失配是封装效应的主要成因[2]。由于不同材料之间参数不匹配，胶高温固化恢复到室温之后，胶层接触面产生残余热应力；另外在加速度计使用过程中不同材料的接触面也会因温度变化而产生热应力。这些热应力与温度相关[3,4]，通过硅结构锚区传递到芯片的敏感结构中，对加速度计输出稳定性产生不利影响。

目前针对粘接胶对封装应力的研究主要分为两类：一是基于粘接胶的角度，研究胶的材料参数、形状尺寸、粘接方式等对封装应力的影响[5,6]；二是基于应力隔离的角度，研究能够减小敏感结构应力与变形的隔离结构[7,8]。大多数研究中，仅将胶视为一个完全弹性材料或一个弹性模量随温度变化的材料，而不考虑粘接胶的粘弹性，即不考虑应力松弛与蠕变。

在硅微谐振式加速度计的样机研制过程中发现，加速度计谐振频率与温度循环次数呈现一定相关性，温度循环前后，单侧谐振器输出发生改变。基于弹性材料建立的封装模型不能完全装模型不能完全反映材料特性与加载历史、时间和温度之间的关系，且封装材料中的粘结胶通常为具有粘弹性的高分子聚合物，在使用过程中会出现应力松弛、蠕变等现象。

为研究芯片粘接胶的参数对热应力的影响，本文建立了一个包括芯片、具有粘弹特性的粘接胶和陶瓷基板的多层硅微谐振式加速度计封装模型，在利用动态热机械分析仪(dynamic mechanical analyzer,DMA)对胶样的特性曲线进行分析的基础上，通过有限元分析的方法研究粘接胶松弛模量、热膨胀系数对芯片应力的影响。

1 硅微谐振式加速度计封装模型

硅微谐振式加速度计采用金属封装，硅—玻璃芯片通过粘接胶与陶瓷基板粘接，陶瓷基板与封装管座的引脚焊接，其中粘接部分形成一个多层结构，如图1所示包括芯片层、胶层与基板，不同结构的材料属性见表1。

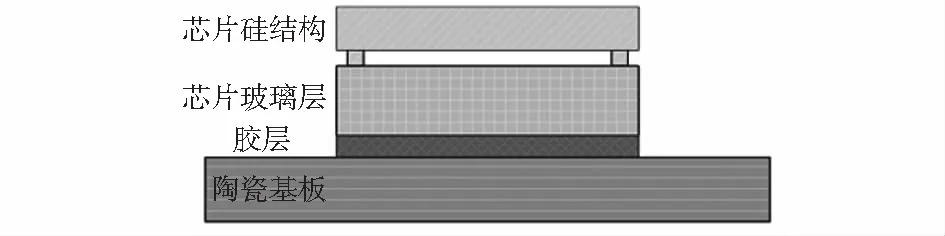
图1 多层结构模型

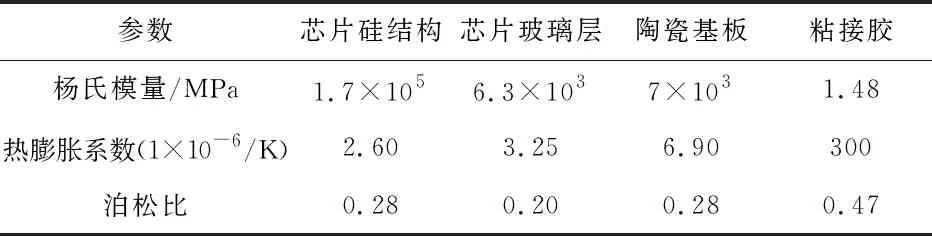
表1 多层结构的材料属性

2 粘接胶的粘弹性建模

2.1 粘弹性本构关系

本文采用广义Maxwell模型描述高聚物的应力松弛行为[9]。广义Maxwell模型由一系列的弹簧—粘壶单元并联而成，如图2所示。

图2 广义Maxwell模型

图2中Ei为第i个单元的弹性元件的弹性系数，ηi为第i个单元的粘性元件的粘性系数，E∞为完全松弛后的模量，n为弹簧—粘壶单元个数。该模型的本构方程可表示为

式中σ(t)为应力，ε0为初始应变，τi=ηi/Ei为松弛时间。由式(1)可得到广义Maxwell模型松弛模量的Prony级数表达式

2.2 应力松弛试验

通过DMA对粘接胶试样进行应力松弛试验，试验温度范围为20～80 ℃，每间隔10 ℃取一个温度点。在每个温度点温度恒定后，对试样施加1 %的恒定应变，并保持20 min，应力松弛结果如图3所示。

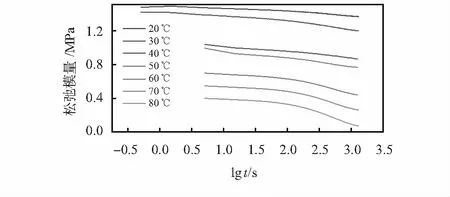
图3 不同温度点应力松弛曲线

基于粘弹性力学中的时温等效原理，以20 ℃为参考温度，在对数时间坐标轴下将其他温度点的松弛曲线向20 ℃平移，得到应力松弛主曲线与对应的移位因子，并用式对移位因子lgαT(T)进行拟合

lgαT(T)=C1(T-T0)+C2(T-T0)2+

C3(T-T0)3

(3)

式中T0为参考温度;C1,C2,C3为多项式拟合的常数项。拟合结果如图4所示，拟合得到C1，C2，C3分别为0.217 67,0.001 38,-4.049 99×10-6。

图4 移位因子及其拟合结果

对平移得到的20 ℃的应力松弛主曲线进行平滑处理，结果如图5所示。基于Abaqus仿真软件得到胶样Prony级数的各项系数如表2所示。

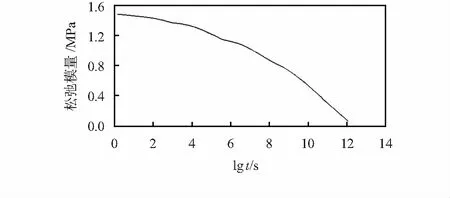
图5 20 ℃应力松弛主曲线

iEi/MPaτiiEi/MPaτiiEi/MPaτi11.88×10-27.170851.02×10-14439791.38×10-17.87×10821.86×10-234.26961.07×10-13.20×105101.65×10-15.78×10937.80×10-2457.3871.10×10-17.48×106111.98×10-13.62×101042.70×10-27843.281.56×10-15.82×107122.97×10-13.85×1011

3 粘弹性参数对加速度计热应力影响的仿真研究

在粘弹性模型的基础上，通过改变粘接胶的材料参数与温度载荷，比较封装结构中的应力。以粘接胶的固化温度120 ℃为参考温度，模拟粘接胶固化之后的温度变化过程，从120 ℃经1 h降温至20 ℃，保温10 h，再经1 h升温至60 ℃，保温10 h，过程如图6所示。

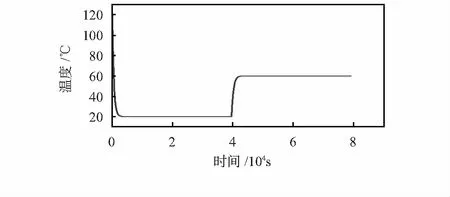
图6 仿真设定的温度载荷

首先对材料应力松弛主曲线的松弛模量进行调整[10]，如图7所示，在应力松弛实验结果的基础上，将松弛模量放大0.5,0.75,1.25,1.5倍，基于Abaqus软件得到粘接层和谐振器振梁中的应力变化如图8所示。降温阶段，胶层和谐振器中应力迅速增加，且应力与松弛模量大小呈正相关;恒温阶段，应力缓慢降低。表3中是胶层应力在20 ℃和60 ℃恒温阶段的变化量对比结果，可见同样时长内60 ℃环境中的胶层应力变化量大于20 ℃环境中的变化量，反映了温度对于材料粘弹性的影响[11]，高温下短时间粘弹性材料的力学表现类似于其在低温下长时间的表现。应力松弛模量大小同样影响应力变化量，胶层松弛模量越大，应力变化越明显。受到胶层应力变化的影响，谐振器中的应力在恒温阶段也有小的变化，如图8(b)所示。

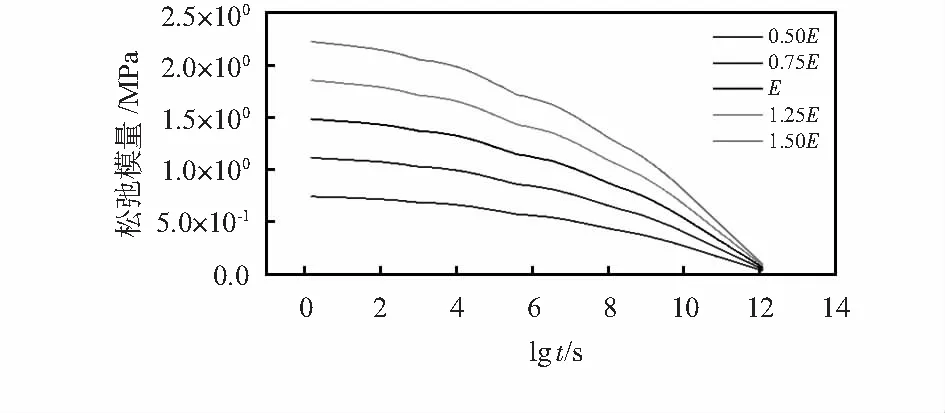
图7 调整后的应力松弛主曲线

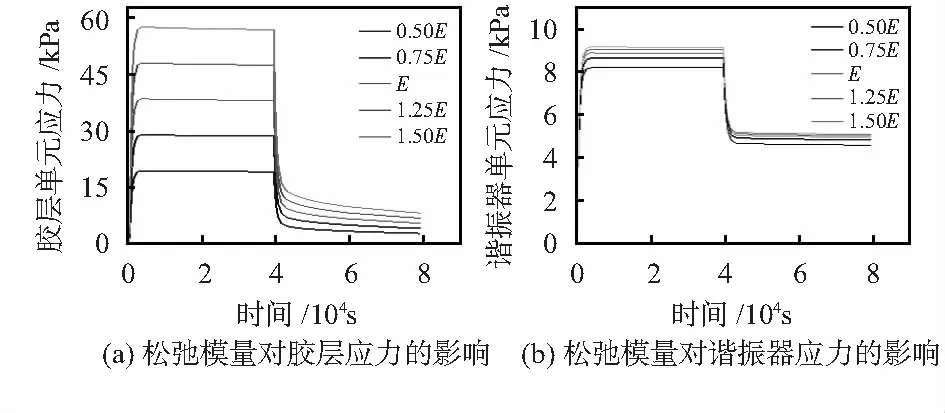
图8 松弛模量对胶层应力和谐振器应力的影响

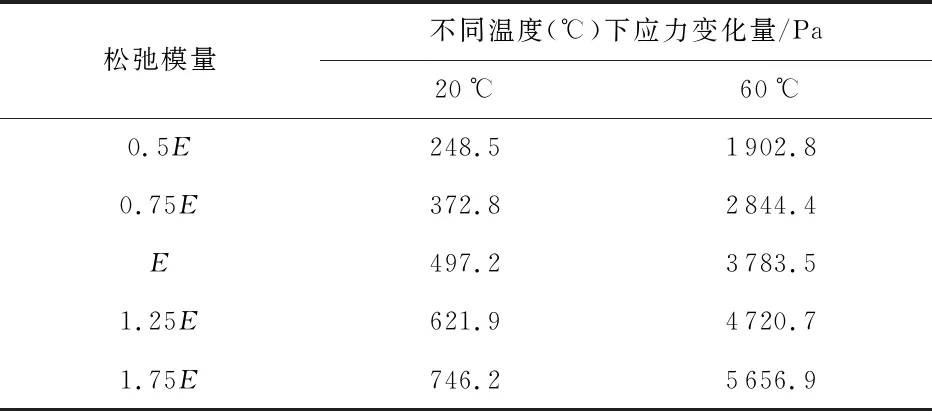
表3 恒温10 h松弛模量变化引起胶层应力变化

为研究粘弹性模型中粘接胶热膨胀系数对结构应力的影响，对不同热膨胀系数(coefficient of thermal expansion, CTE)的粘接胶模型进行了计算，粘接层和谐振器振梁中的应力变化分别如图9所示。粘接胶的CTE越接近于被粘接材料(玻璃与陶瓷)的CTE，温度应力越低。恒温阶段胶层应力变化量如表4所示，60 ℃恒温过程的应力变化量大于20 ℃；CTE数值越高，应力变化量也越大。由于粘接胶的CTE通常大于被粘接材料，因此,选择低CTE的粘接胶更有利于加速度计的温度稳定性与长期稳定性。

图9 CTE对胶层应力和谐振器应力的影响

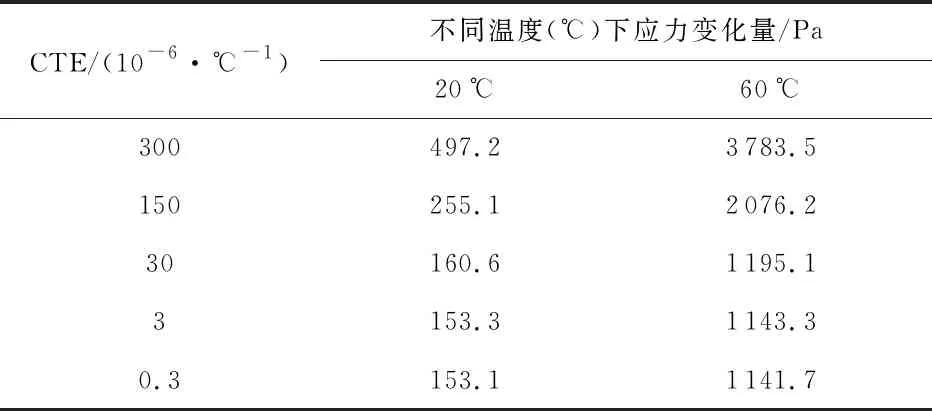
表4 恒温10 h CTE变化引起胶层应力变化

为了研究循环温度载荷对加速度计热应力的影响，对降温后的模型施加如图10(a)所示的循环温载荷，每次循环从20 ℃经40 min升温至60 ℃，保持400 min后经100 min降温至-40 ℃，保持400 min后经60 min再次升温至20 ℃，即相邻标记间为一次循环，模型共经历4个循环。提取胶层单元在温度循环中的应力，如图10(b)所示。温度循环过程中60 ℃对应的热应力远远低于-40 ℃时的应力，CTE越低，高低温之间应力的变化量也越小。对CTE为300×10-6/℃的仿真曲线进行分析，比较单次循环前后残余热应力的大小，如表5所示。每次循环后应力值都较循环前有所减小，循环结束后，高温固化导致的残余热应力从38 320.9 Pa降低至28 286.4 Pa，变化量为10 034.5 Pa。比较不同模型循环前后的应力变化量，则降低CTE能够减小应力的变化量。与CTE的影响趋势类似，较小的松弛模量对温度循环中应力的应力变化影响较小，如图10(c)所示。

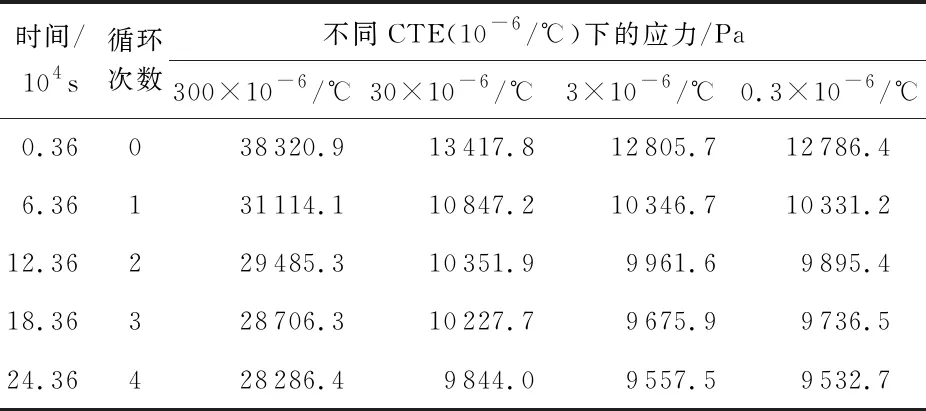
表5 温度循环前后残余热应力大小

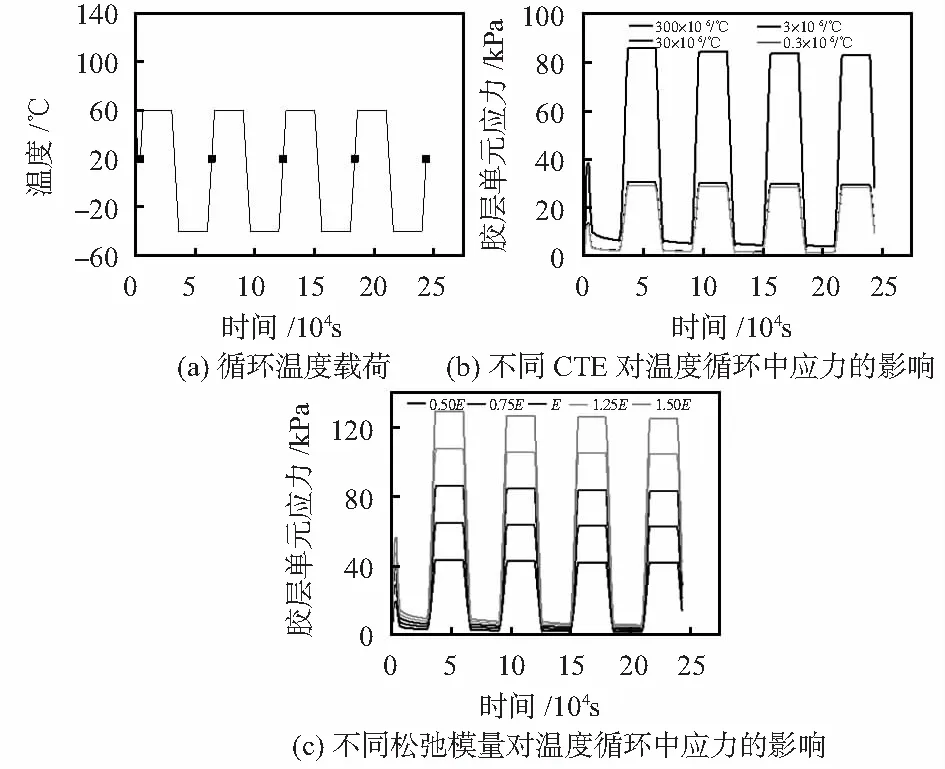
图10 循环温度载荷对加速度热应力的影响

4 结束语

仿真结果表明：粘接胶应力松弛曲线模量和CTE越小，模型热应力越低，且在恒温环境中，由粘弹性导致的应力变化也越小；环境温度与温度载荷的循环次数也是影响应力变化的重要因素，环境温度越高，应力减小的速度越快，经历的循环次数越多，残余热应力越小。因此，低松弛模量和CTE接近被粘接材料的芯片粘接胶更有利于硅微谐振式加速度计的热稳定性与长期稳定性。