基于灰狼优化算法的混凝土坝变形监控模型
陈淑云,周稳忠,谷艳昌*,王 宏
(1.宜兴市横山水库管理所,江苏 宜兴 214200;2.南京水利科学研究院,江苏 南京 210029;3.水利部大坝安全管理中心,江苏 南京 210029)
改革开放以来,中国水利水电事业发展迅速,水库大坝建设取得了显著成就[1]。水库大坝是优化水资源配置、调度水资源时空分布的重要工程措施。截至2017年,中国已修建各类水库98 795座,其中大型水库732座,总库容9 035亿m3;中型水库3 934座,总库容111亿m3[2]。由于历史原因,中国水库大坝多建设于20世纪50年代左右,许多大坝存在防洪标准低、施工质量差等安全隐患问题。随着时间的推移,大坝出现了不同程度的老化和病变问题,存在诸多安全隐患,随时威胁着下游城镇人民的生命财产安全。
为实时掌握大坝运行情况、判断大坝安全性态,目前最有效的办法是对大坝进行安全监测,并对监测数据进行分析[3]。其中大坝变形监测资料能最直接的反映大坝运行状态,变形监测资料数据分析方法分为定性和定量分析,主要是通过研究其时空分布规律,运用数学分析方法建立变形量及其影响因素之间的数学模型,预测变形发展趋势,评估大坝服役状态。常见数学模型包括统计模型、确定性模型、混合模型,统计模型是利用监测序列资料,通过数学回归计算方法,估计监控模型的待求参数,进而建立统计监控模型。确定性模型是用有限元法对计算值与实测值进行最小二乘法拟合,建立了可靠的高精度模型,吴中如院士首次在国内将确定性模型用到佛子岭拱坝坝顶水平位移分析中[4]。混合模型则是水压分量用有限元计算值,其他分量用统计分量而建立[5]。近年来,人工神经网络和支持向量机等方法发展迅速[6-7],逐渐被众多学者运用到大坝监测数据分析中来,并将神经网络与各种算法相结合[8-9],使大坝安全监测资料研究体系更加完善和全面。李月娇等[10]运用改进的自适应遗传算法对参数进行寻优,全局搜索能力更强,泛化能力更好,进一步提高了模型拟合效果和预测精度。随着新型种群智能仿生算法的发展,如粒子群算法、蚁群算法、蜻蜓算法等[11],进一步推进了大坝变形监控模型的发展,这些算法在模型的拟合效果和预测精度方面效果较好,相较于传统的数学回归方法优势更大。
灰狼算法(Grey Wolf Optimization, GWO)是Mirijalili等[12]通过研究狼群生活习性,于2014年提出的一种具有竞争性的新型群体智能优化算法。现有研究表明,灰狼算法具有复杂度低、控制参数少、搜索能力强、效率高等特点,在求解精度和稳定性上具有明显优势[13]。目前GWO算法已成功应用于电力系统、经济调度指派、车间调度等[14-15]。本文引进灰狼算法分析某混凝土重力坝变形测点监测数据,进一步优化大坝变形模型。
1 灰狼算法(GWO)基本原理
灰狼是大自然界中顶级食肉动物,通常被视作顶级杀手并且处于食物链的最顶端。狼群具有严格的等级制度和分工制度,可描述为金字塔等级制,将灰狼群体分为4层:α、β、δ和ω层,见图1。
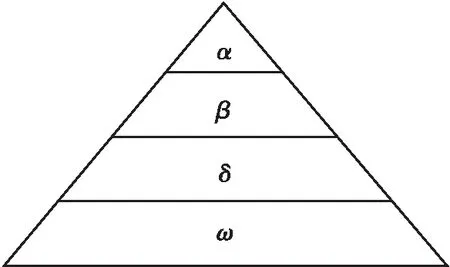
图1 灰狼等级金字塔
每个狼群里灰狼的平均数量为5~12头。在灰狼算法中,等级最高的是头狼,被标记为α,是狼群的主要管理者,负责狩猎、狼群的决策以及整个狼群的领导。β层狼的主要功能是当头狼α位置空缺时,β则顶替成为α,具备头狼α的权利,支配狼群中其他成员的活动。下一层狼称为δ,δ听从α和β的指令。金字塔最底层狼称为ω,主要负责种群内部关系的平衡。狼群中下一层级必须严格服从上一层级的领导,并进行群体狩猎行动。
灰狼算法的主要灵感来源是灰狼群体严格的社会等级制度以及灰狼的狩猎方式。灰狼群体的捕食行为分为包围、猎捕以及攻击3步骤。
a)包围。狼群捕食狩猎首先是对目标进行包围,确定狼群个体与待捕猎物之间的距离,数学模型可以描述为:
(1)
(2)


(3)
(4)

b)捕猎。在狼群对猎物实施包围后开展捕猎行动,在捕猎过程中通常由α、β、δ的位置模拟灰狼的狩猎行为进行位置更新,在迭代过程中保存历史的前3个最优值(即狼群狩猎最优位置),种群中其他灰狼群通过最优值的位置更新而不断更新自己的位置。灰狼群在进行狩猎时数学表达式描述如下:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
由式(5)—(7)确定群内个体与α、β、δ的距离,然后由式(8)—(10)可以确定更新后的灰狼位置,由式(11)可确定猎物所在位置。灰狼算法最优解向量位置更新过程见图2。
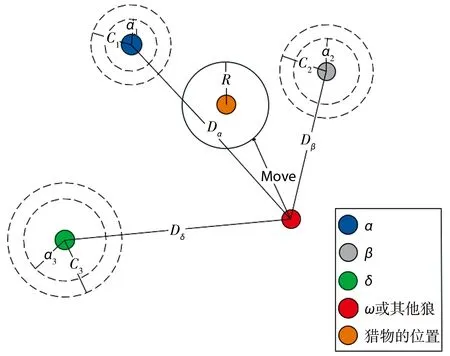
图2 GWO中灰狼的位置更新过程
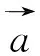
2 灰狼算法(GWO)的计算流程
通过前文对灰狼优化算法包围、捕猎和攻击3步骤的阐述,总结出灰狼优化算法的大致计算步骤。
a)设置灰狼算法各参数数值:灰狼狼群的规模N,最优解求解总迭代次数tmax,待求变量的取值范围,随机生成α、A、C等参数、初始化灰狼种群位置。
b)计算N个个体灰狼所处位置的适应度值;选择3个位置适应度值最好的灰狼,记录其位置向量为Xα、Xβ和Xδ。
c)用式(5)—(11)更新其余灰狼的位置。
d)用式(3)—(4)更新参数α、参数A和参数C。
e)重新计算狼群个体的位置适应度值,与上一次计算结果相对比,重新选择个位置适应度最好的灰狼作为下一代,判断结果是否已满足条件,如果不满足条件则重复进行(2)—(5),继续进行迭代计算。若迭代次数达到设定的最大迭代次数tmax,停止寻优计算。
根据灰狼优化算法操作步骤,绘制GWO流程,见图3。
3 工程实例
某水利枢纽工程由拦河大坝、右岸地下电站厂房、左岸岸边通航建筑物及灌溉渠首工程等建筑物组成,水库总库容17.41亿m3,属于大(1)型水利工程,防洪库容7.4亿m3,为年调节水库。大坝为碾压混凝土重力坝,最大坝高131 m,坝顶宽12 m,总长368 m,坝顶高程245 m。大坝布置了视准线、引张线、倒垂线、正垂线、裂缝计和测缝计等监测设施。
3.1 建模
选取3号坝段2013—2014年坝顶变形监测数据作为训练样本进行分析,剔除异常数据后保留71组位移监测数据,将1—11月共65组数据作为模型训练样本,12月份6组数据进行预报分析。
大坝坝顶位移与水位值、温度量和时效值之间的关系见式(12)。
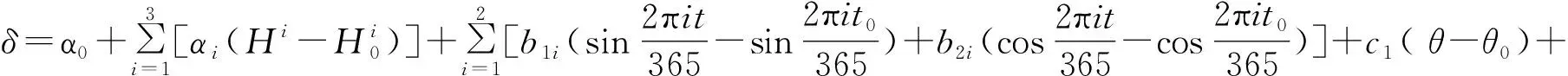
(12)
式中H、H0——监测日和始测日的上游水头,m;t、t0——监测日和始测日至时间起算日的累计天数,d;θ、θ0——监测日和始测日至时间起算日的累计天数t、t0除以100;αi、b1i、b2i、c1、c2——各效应分量的回归系数;α0——常数项。
设置狼群个体N=10,待求系数范围为[-1~1],求解总迭代次数tmax=100,通过自编灰狼算法程序,建立大坝变形模型目标函数。
为了对比模型精度与预测效果,同时运用逐步回归法和BP神经网络进行变形模型的拟合以及结果预测[16]。
灰狼优化算法和逐步回归法拟合结果见表1,根据模型拟合和BP神经网络计算结果,绘制实测变形值、GWO模型变形值、逐步回归模型变形值和BP神经网络拟合变形值过程线和残差过程线,见图4、5。
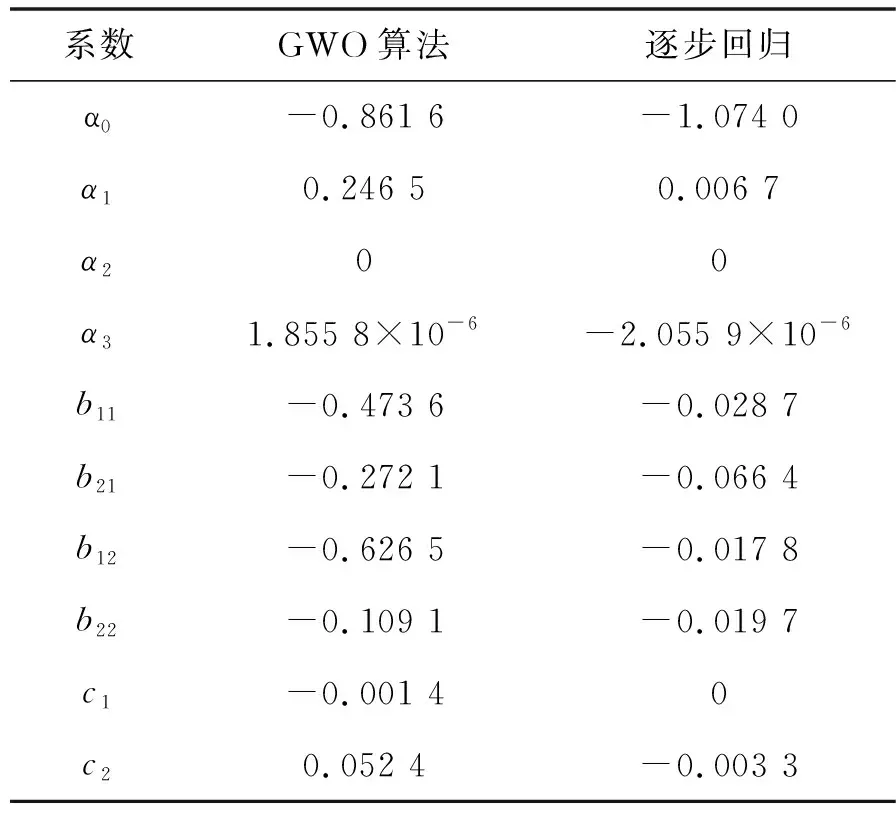
表1 回归分析结果

图4 实测、GWO、逐步回归和神经网络变形值过程线

图5 GWO、逐步回归和神经网络变形残差过程线
3.2 模型拟合效果评估
为衡量计算模型精度,采用复相关系数R进行判别,具体公式见式(13)。
(13)
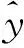
复相关系数R越大,表示因变量与自变量线性组合的密切程度越好,统计模型建立的因变量与自变量之间线性关系越好。一般认为当复相关系数R≥0.80时,实测值与回归值的偏差较小,回归模型的精度较高,拟合结果满足要求。
经计算,GWO模型的复相关系数为0.990,逐步回归模型复相关系数为0.946,BP神经网络拟合结果复相关系数为0.973。三者精度都满足要求,但是GWO模型相比于逐步回归模型和BP神经网络拟合效果更好,更符合实测值变化情况。
3.3 模型预测评估
为进一步评估模型的准确性和适用性,根据计算模型和BP神经网络预测12月份的位移值,实测值与预测值结果见图6。

图6 GWO、逐步回归和神经网络变形预测值与实测值
采用平均绝对误差MAE和均方根误差RMSE评价模型预测的精度,具体公式见式(14)、(15)。
(14)
(15)
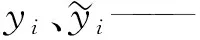
MAE与RMSE值越小,则表示模型预测精度越高,计算结果见表2。

表2 MAE和RMSE计算结果统计
根据图6以及表2可知,相比于传统逐步回归模型和BP神经网络,GWO模型预测变形值结果更符合实际情况,预报误差更小,验证了GWO模型在大坝变形拟合和预报过程中的适用性。
4 结论
针对大坝变形资料分析建模问题,本文通过研究灰狼算法(GWO),提出基于灰狼优化算法的大坝变形模型建立方法,并将本算法拟合和预测结果与传统逐步回归方法作比较,主要得出以下结论。
a)灰狼算法(GWO)算法作为新型智能算法,具有复杂度低、控制参数少、搜索能力强等特点,用于分析大量位移监测数据,建立位移模型上具有明显优势。
b)运用灰狼算法(GWO)算法建立的位移模型相比于传统逐步回归分析和BP神经网络结果,在拟合和预测精度上都得到明显的提升,验证了GWO模型在大坝变形拟合和预报过程中的适用性。
c)灰狼算法(GWO)运用中应注意,灰狼狼群的规模一般取值5~15即可,本文取值10所建模型精度已经明显提高;待求变量的取值范围,需要依据待求问题实际情况并凭借工程经验确定或试算,同时调整最大迭代次数,防止算法陷入局部最优。

