非平稳工况下振动信号数字积分方法优化

连而锦

（明阳智慧能源集团股份公司，广东中山 528400）

0 引言

在工程应用中，对于低频的大型结构系统，位移的测量通常较为困难和复杂，无法保证可靠性和准确性。相对于位移测量来说，加速度测量的应用却相当广泛，技术比较成熟。理论上，通过测量得到的加速度信号进行两次数字积分可得到相对位移信号。目前常用的数字积分方法有时域积分和频域积分。

时域积分[1-2]常采用梯形公式或辛普森（Simpson）求和公式，大都采用多项式拟合方法去除积分后的一次二次和高次趋势项。但在高噪声的工况下，多项式拟合去趋势无法消除积分过程中因噪声而产生的低频摆动趋势。

频域积分[3-4]利用傅里叶正、逆变换，积分在频域内对傅里叶系数进行简单的除法运算，可避开时域积分微小误差累积导致的趋势项偏差问题。对于低频段噪声增益放大而引起的积分误差，可通过设置截断频率的方式进行滤除[5-8]。然而，基于傅里叶变换及频率计算的频域积分方法不适用于非稳态信号[4]。

大型风电机组上一般都安装有低频振动传感器，用于测量机组塔架频率；由于机组内旋转设备多，噪声水平高，特别是偏航及收桨时，将引入瞬态激励，导致计算塔架的相对位移时，出现较大偏差。通过分析上述数字积分方法的实现原理并结合工程实际，提出基于Hodrick-Prescott算法的时域积分方法，对风电机组工程实际信号进行分析及实例验证。

研究结果表明，采用新算法的时域积分方法由于去除了低频摆动趋势，在非平稳、高噪声的工况下能提供准确的积分位移信号，通过误差评价指标表明其综合性能最优。

1 数字积分及其误差分析

1.1 多项式去趋势的时域积分

时域积分常用矩形公式法、梯形公式法和辛普森（Simpson）求和法。它们实际上是通过相邻点之间的矩形、梯形和二次曲线来逼近积分区域，由于辛普森（Simpson）积分逼近的精度高，计算公式也相对简单，是工程计算中常用的时域积分方法[9]。

由于加速度信号通过加速度传感器获得，其加速度初始值往往不为零，加速度传感器也存在着因环境因素影响导致的零点漂移，伴随着信道传输的噪声以及信号采集过程中的离散和量化误差产生的噪声，这都给积分过程带来了累积误差。可通过式（1）来表达，可以看出速度和位移信号中分别含一次项和二次项。所以在积分过程前后均需要进行多项式拟合以消除趋势项，才能得到有效的振动速度和位移信号。

式中：a(t)为加速度信号；v(t)为速度信号；s(t)为位移信号；c0、c1、c2分别为积分过程带来的累积误差系数。

相关学者已经以多项式去趋势的时域积分进行了大量的仿真分析。顾名坤[4]指出，实际振动加速度信号积分后含有的复杂非线性趋势项很难采用确定的函数拟合，说明去除趋势项的时域积分难以使用于实测振动信号。董礼[5]指出，由于振动噪声的存在，使积分后的振动信号含有一定的低频摆动趋势。成勋[8]指出，时域积分的误差主要来源于积分产生趋势项累积误差，并且趋势项无法完全消除。

1.2 频域积分及其误差分析

频域一次积分、二次积分可用式（2）进行表示。其表述为，频域积分先将需要积分的信号做傅里叶变换到频域，积分运算就变成了在频域内的傅里叶分量系数的除法运算，将运算的结果再经傅里叶逆变换得到积分后的时域信号。频域积分不仅提高了运算效率，而且可有效避免时域微小误差在积分过程中的累积放大。

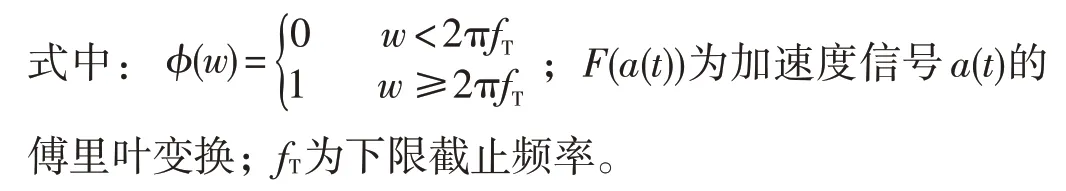
可通过分析理想积分器的幅频特性曲线，来说明频域积分的误差来源。其在0.16 Hz（1 rad/s）以上的积分频带内具有-20 dB/十倍频的衰减特性；而在0.16 Hz以下的频段，其具有20 dB/十倍频增益放大作用。在实际工程应用的积分器，总有其需求的下限截止频率fT，为了避免低频段的增益放大而产生积分误差，低于下限截止频率的幅值最好是衰减的或者截断。

然而，基于傅里叶变换及频率计算的方法不适用于非稳态信号[4]。现场运行工况若不满足稳态信号的要求，这时若使用频域积分将产生很大的积分误差，应改用其他方法。

1.3 改进型的时域积分

考虑到多项式拟合去趋势无法消除积分过程中因噪声而产生的低频摆动趋势，并且工程现场测定的振动信号都不可避免会包含有噪声，正常情况下，为了提高信噪比，可通过相关的降噪技术在积分前先实现噪声信号的滤除[10]，但无法达到理想状态。为了能进一步去除时域积分的摆动趋势项，这里提出使用Hodrick-Prescott趋势分解模型[11]来去除振动噪声引起的低频摆动趋势。

Hodrick-Prescott趋势分解模型是一种信号分离方法，广泛应用于经济数据中经济趋势和周期波的分离。其基本原理为求解一个趋势序列，使其满足分解的趋势序列和周期序列能量的加权和最小，其目标函数定义为如下：

式中：yt为原时间序列；gt为分解的趋势序列；α为趋势项的加权系数，当α趋近0，分解的趋势序列gt趋近yt；当α趋近∞，分解的趋势序列gt趋近于yt的线性拟合。

基于Hodrick-Prescott算法的时域积分流程可采用图1实现。

图1 改进型算法的时域积分流程

2 误差评价指标

为方便评估结果波形的差异，引入平均峰值误差、平均最大相对误差及平方和误差的概念[7]。

平均峰值误差反映了积分信号波形与实测信号波形最大范围的吻合度：

式（4）～（6）中：X(t)为积分信号；S(t)为实测信号。

3 工程实测数据分析

风电机组机舱上通常都安装有加速度传感器测量机舱前后、左右的振动信号，测得在风电机组停机过程中产生的左右振动加速度信号，其采样频率为100 Hz，如图2所示。

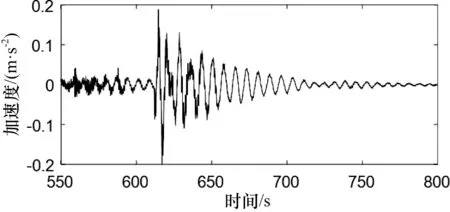
图2 实测振动加速度信号

经多项式去趋势时域二次积分得到的位移信号如图3所示。从位移数据来看，其存在明显的摆动趋势，这积分结果是不正确的。

图3 实测信号的多项式去趋势时域积分

采用频域二次积分的位移信号与采用改进型算法的时域二次积分的位移信号如图4所示。

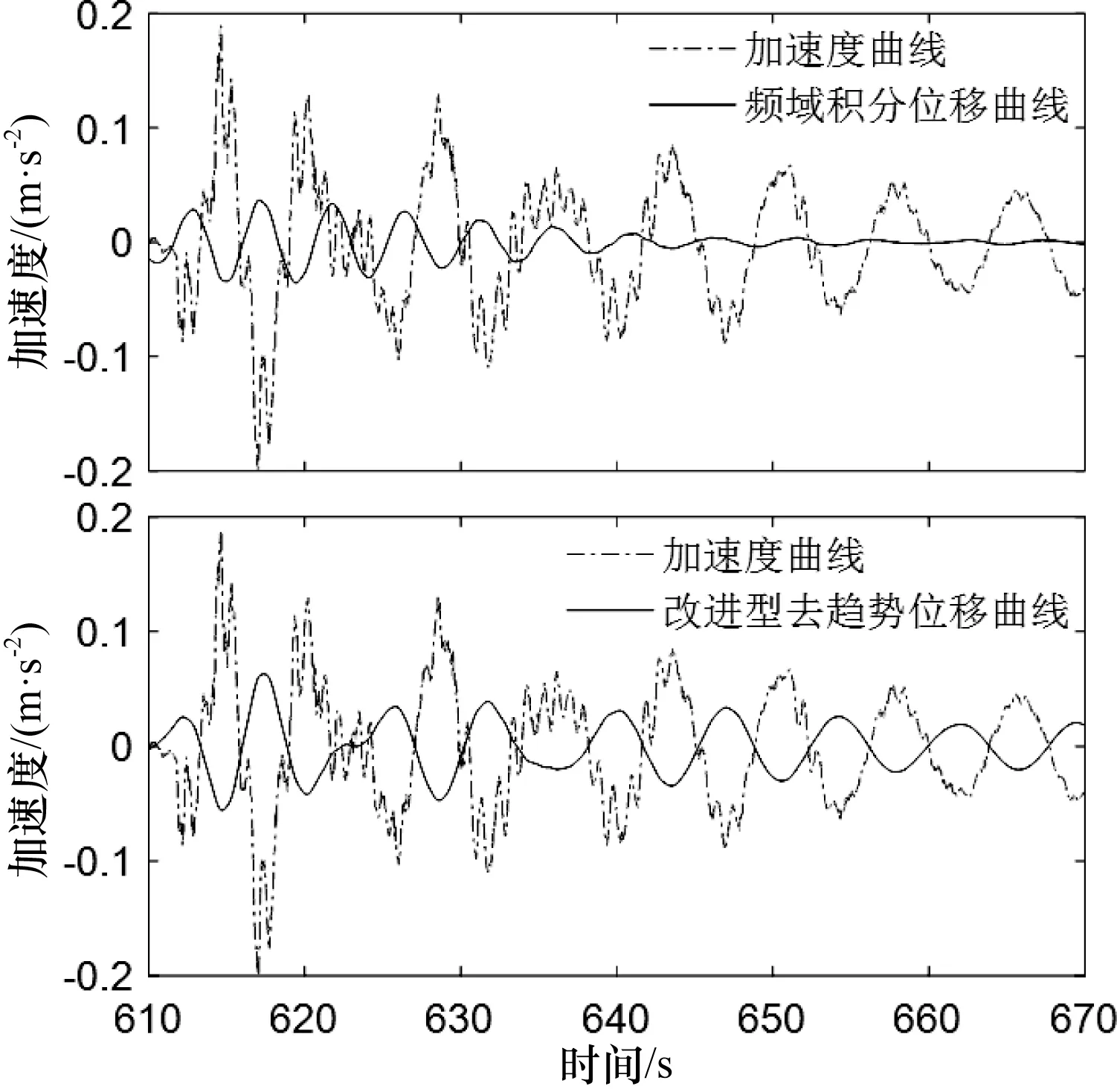
图4 实测信号积分后的位移信号

由于停机时收桨动作导致振动过程的非平稳性，采用频域积分的位移信号出现了较大的畸变，仔细观察其位移峰值明显偏小，位移相位也不再与振动加速度有180°的严格偏差，所以，积分结果不准确。

采用改进型去趋势时域二次积分的位移信号其波形与振动加速度波动十分相似，并且其位移相位与振动加速度保持严格的180°偏差。可见，在非平稳、高噪声的工况下该积分方法较为准确。

4 Bladed仿真数据验证

为验证上述不同积分方法的积分误差大小，需利用风电机组设计仿真软件Bladed对机组建模，执行发电工况dlc1.2计算，得到相关过程数据。

分别对过程数据中的Bladed机舱前后、左右振动加速度信号进行二次积分后得到位移信号，再与过程数据中的Bladed位移数据进行比较，如图5～6所示，并计算积分误差，将结果汇总在表1中。

表1 机舱前后、左右的加速度信号时频域二次积分误差计算

图5 积分后的机舱前后位移信号总体对比

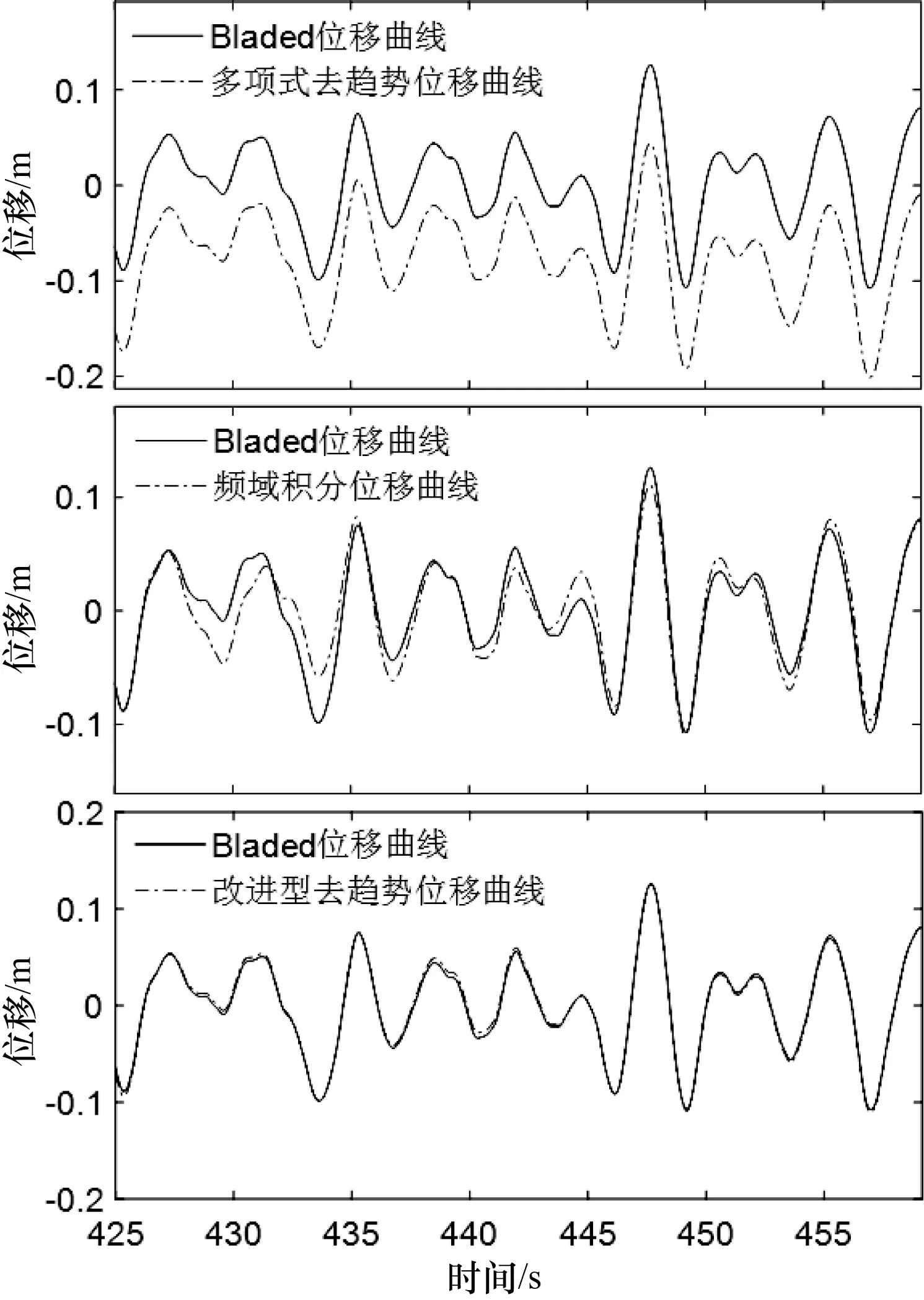
图6 积分后的机舱前后位移信号细节对比

从图5～6可以看出，采用多项式去趋势的时域二次积分位移信号由于噪声的存在，出现了明显的摆动趋势项，其积分误差也最大。

从表1中看到，采用改进型算法的时域二次积分位移信号具有最高的积分精度，平方和误差可达3%～8%，与Bladed计算的过程数据中的位移信号最为贴近，而频域二次积分方法次之。这是由于风电机组的机舱振动中包含有叶片、传动链等多体耦合频率成分和噪声信号。所以，采用改进型算法的时域积分方法优于频域积分方法。

5 结束语

通过工程实测数据分析和Bladed仿真数据验证，结果表明：（1）采用多项式去趋势的时域积分方法信号噪声敏感，仅适用于较理想的低噪声信号；（2）频域二次积分方法由于其积分过程是在频域内对傅里叶系数进行简单的除法运算，低频摆动趋势分量小，在平稳工况下，积分精度高，但不适用于非稳态信号的积分；（3）采用改进型算法的时域二次积分方法由于去除了低频摆动趋势，该方法在非平稳、高噪声的工况下能提供准确的积分位移信号，平方和误差可达3%～8%。

由于大型风电机组内旋转设备多，噪声水平高，转子转速跟随风速动态变化，特别是偏航及停机收桨时，存在瞬态冲击，结合多体耦合频率，使得塔架振动信号具有明显的非平稳信号特点。采用改进型算法的时域积分方法对该复杂工况下的塔架振动加速度进行数字积分能得到高精度的相对位移信号，对风电机机组塔架结构系统的分析和诊断有重要的实用意义。