基于点列阵光源的自由曲面透镜设计

李镇真，黄伟杰，林浩涛，黄晨华，李湘勤

(韶关学院 智能工程学院，广东 韶关 512005)

以LED为光源的自由曲面透镜，在道路照明、汽车前照灯、投影仪设备和扫描打印等领域具有广泛的应用。目前主流照明器件采用的匀光方式主要是重叠法(Superposition)[1]，光学系统中，以复眼(Lens Arrays)或锥棒 TLP(Tapered Light Pipe)为核心的照明结构均利用重叠法匀光。LED的发光旋转对称，若要照明其他形状的目标面，需借助其他光学器件，如，液晶显示器 (Liquid Crystal Display，LCD)投影仪通过复眼透镜，数字光处理器(Digital Light Processor．DLP)通过方棒和透镜组实现对数字微镜(Digital Micro—mirror Device，DMD)面板的均匀矩形照明[2]。采用上述两种结构不仅会增加光学系统的复杂度，还存在光路复杂、光能利用率低等问题。针对LCD光固化打印技术对透镜的需求，使用以上方法设计的透镜将增加光固化打印机的体积，降低光能的利用率。自由曲面器件因其可以满足各种照明形状的要求得到了广泛的应用，2001 年 OEC公司的Ries和Muschaweck提出通过数值求解微分方程的方法来构造自由曲面面型的器件[3-4]。自由曲面的设计目前主要有数值优化法和直接法[5]，数值法是通过对已有光学结构解析式设置可变参数来调整结构的方法，该方法在建立新的模型时十分繁琐，对设计人员的经验要求高。使用“直接法”设计自由曲面透镜，可提高设计过程的可控性和设计效率，直接法包括SMS 法、MA 等式法、剪切法等。Rise等[3]利用裁剪法，通过裁剪光学曲面控制波前，最终将光学曲面模型的求解转换为数学模型求解，即求解一组非线性偏微分方程[6-8]，该方法不能根据指定的光学曲面进行设计。根据光源的分布特性和矩形照度分布等要求，基于微分几何理论[9-10]和能量守恒原理及拓扑关系[11-12]建立微分方程组，使用Runge-Kutta算法求解微分方程组，通过Matlab对微分方程编程计算求得自由曲面数据，再利用 3D 建模软件对离散点数据进行拟合形成自由曲面。

一般而言，当透镜的口径与光源口径比值大于5时，光源可以简化为点光源；当两者比值小于5时，光源应被当作扩展光源。设计时，若设定透镜的口径大于所用点列阵光源边长的5倍，即可将光源简化为点光源处理。

液晶屏数字透射光固化3D打印技术，即LCD光固化3D打印技术，精度高、原理简单，使用广泛，是桌面级3D打印设备常用3D打印技术之一。LCD光固化3D打印设备通常采用矩形液晶屏，并拆除背光板，紫外LED发出的特定波长光束经液晶面板上按需打开的光通道照射树脂，引发树脂聚合固化。LED光源投射在受照面的光强均匀性是影响LCD光固化3D打印技术打印精度和一致性的主要性能指标之一，因此，有必要对光源做一定的匀光处理，以提高受照面光强均匀度。根据LCD光固化3D打印设备所使用点阵光源及对矩形受照面均匀照度的要求，结合点列阵光源的特性，利用微分几何理论和折射定律推导光线与曲面透镜的关系，设计高均匀度的单一透镜，以提高LCD光固化3D打印设备在矩形受照区的光均匀度。

1 设计原理

入射光线在自由曲面上的p点发生折射，矢径op可记为

op=ρI=ρsinθcosφ，ρsinθsinφ，ρcosθ

(1)

式中：θ为入射光线与Z轴正方向的夹角，φ为入射光线投影到XoY面后与X轴正方向的夹角，ρ为矢径op的长度，I为入射光线的单位矢量。又设目标面上t的坐标为(x，y，z)，则出射光线的单位矢量为

(2)

设自由曲面上p点的切向矢量分别为pθ和pφ。则自由曲面上法向矢量为

N=pθ⊗pφ

(3)

根据三维空间坐标中的斯涅耳定理可得

(4)

式中：no和n1分别为折射光线和入射光线所在空间介质的折射率。式(4)两边同时点乘pθ和pφ，且pθ⊗pθ、pφ⊗pφ，因上式中I·pθ=ρθ；I·pφ=ρφ，则

(5)

在理想情况下，光束在自由曲面透镜中的折射或反射没有能量损失，也不考虑介质的吸收影响，因此，能量守恒定律入射能量与出射能量相等。将光源所处位置设为坐标原点，由光源的辐射光通量和能量守恒定律可得

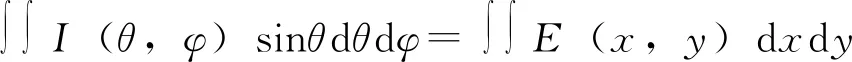
(6)

式中：I(θ，φ)为光源的光强，dΩ为光源发出光线的球坐标中的立体角，E(x，y)为矩形受照面的照度分布，且为常数。设矩形受照面的长度和宽度分别为l和w，LED近似为朗伯光源，配光I(θ，φ)取I0cosθ，可以得到在第一象限内目标面上的坐标t(x，y，z)与θ和φ的关系为

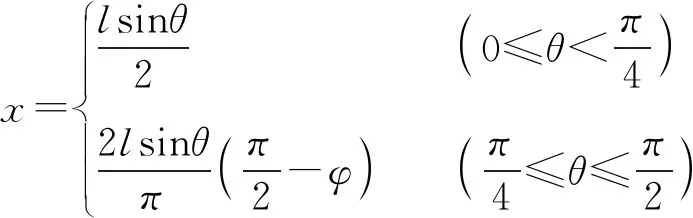
(7)

根据式(5)和式(7)，令n1=1，n0=n得自由曲面透镜得微分方程为

(8)

利用Runge-Kutta算法求解方程组(8)，z0为1 000 mm，点列阵光源与自由曲面中心的距离ρ0为32 mm，矩形被照面长度l为120 mm，宽度w为68 mm，折射率为1.518 72，可得到自由曲面透镜的数值，图1为拟合得到的曲线图形，表1、表2为当φ分别为90°和0°时t点对应坐标值，将这些数据拟合成曲面，可得到自由曲面透镜为一个类似花生米的模型，如图2所示。

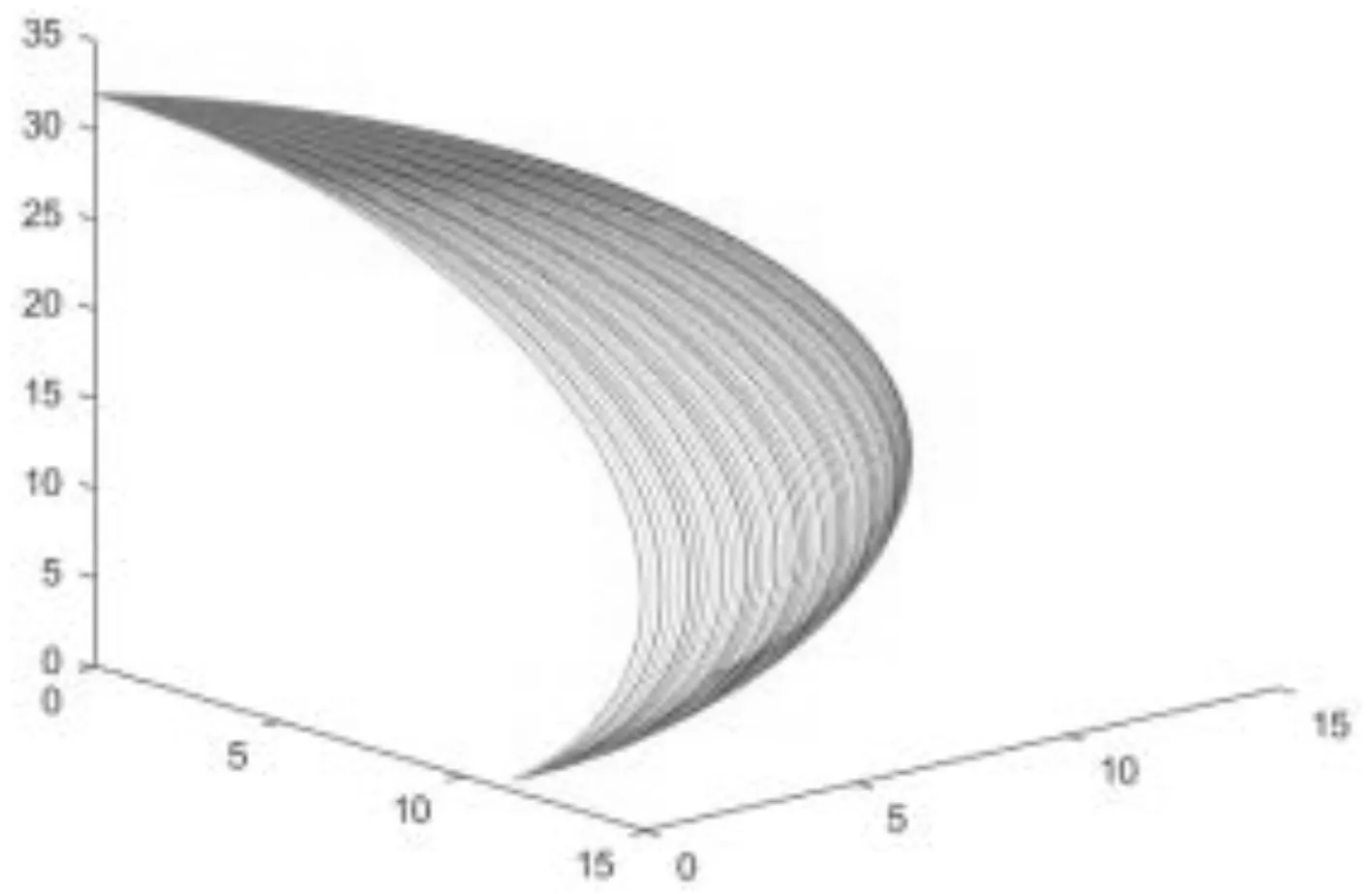
图1 拟合曲线图形

图2 自由曲面透镜模型

表1 当φ为90°时的曲线数据

表2 当φ为0°时的曲线数据

2 仿真与分析

将得到的离散点数据进行三维建模，得到类似花生米状自由曲面透镜的三维模型，再对该模型一定比例切割得到自由曲面透镜，当输入不同的矢径ρ时，可以得到不同大小的透镜。多次仿真结果显示，当ρ取32 mm时，矩形受照射面可获取最佳的光强均匀度，因此，设定ρ为32 mm。由于花生米状透镜难以加工，还需对花生米状模型进行修型，最终获得一个长轴为38.9 mm、短轴为29.0 mm、高度为14.5 mm的半椭圆模型，如图3所示。

图3 自由曲面透镜

修正模型后，对自由曲面透镜进行仿真分析，设定光源芯片为1.1 mm、间距为0.2 mm的4×4的点列阵光源，进行光线追迹，得到光线通过该自由曲面透镜时的照度分布如图4所示。从图4(a)可以看出，在矩形受照面中部照度较为均匀，矩形受照面4个角度光照度值变化较大。图5为被照面与透镜距离为100 mm时的照度效果图，从图中可以看出矩形受照面全域照度较均匀，其光能利用率为48.263%。根据美国国家标准ANSI/APMIT.228—1997[13]，计算得到其均匀度为88.3%，采用该标准进行均匀性计算的取样数据如表3所示。

表3 区域照度取样值 lx

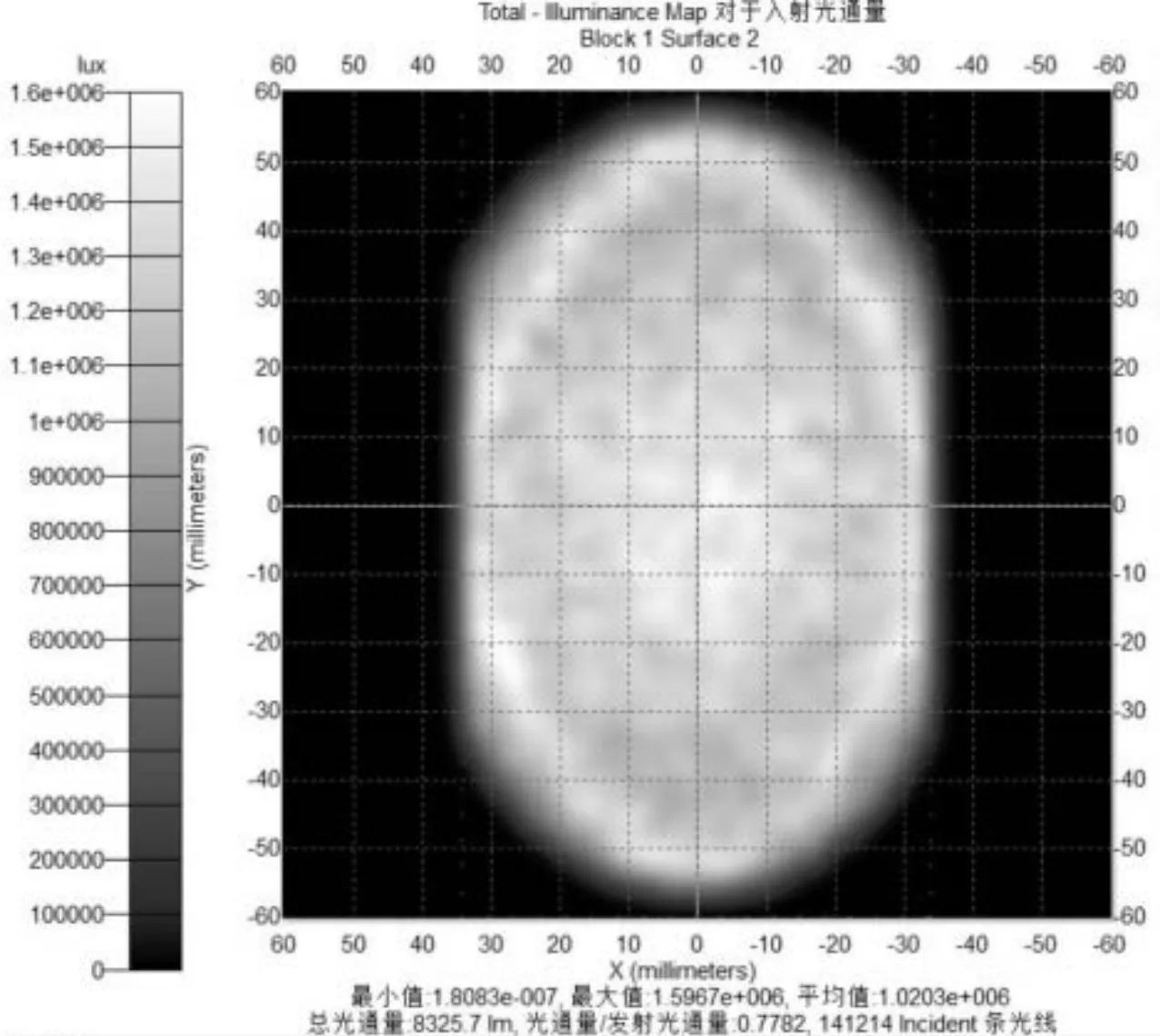
(a)光斑图

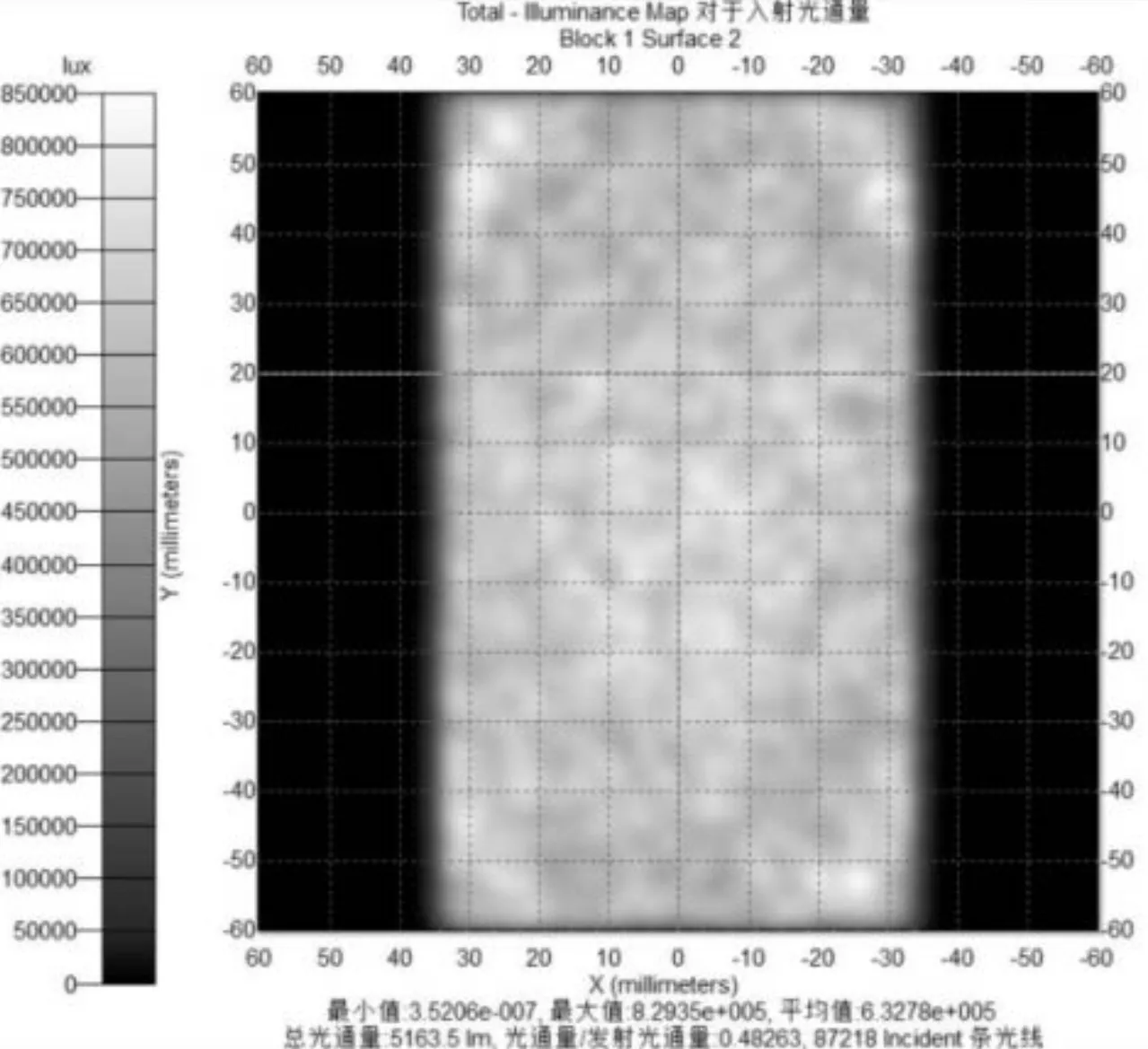
(a)光斑图

因此，当设定ρ为32 mm时，受照面与透镜距离100 mm的透镜光能利用率达到48.26%，其均匀度到达88.2%以上。表4是受照面与透镜不同距离对应的光能利用率和均匀度数据， 从中可以明显看出，80～100 mm距离区间内，均匀度随着距离的增大而增大，光能利用率随着距离的增大而减小。

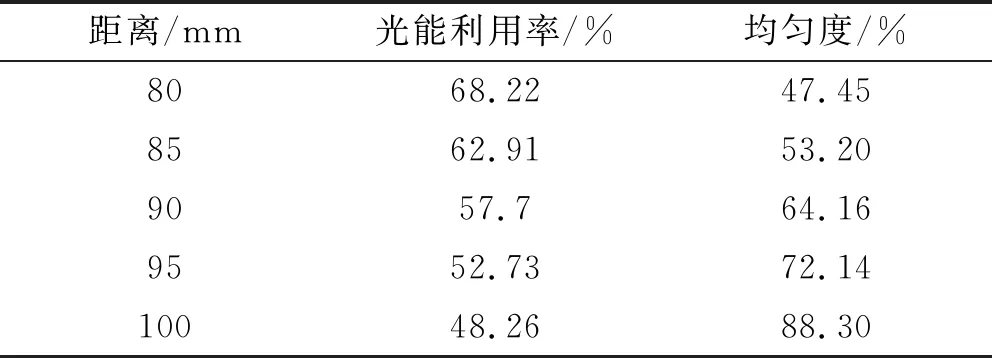
表4 光能利用率与均匀度与距离变化关系

3 结论

基于LCD光固化打印技术对透镜出射光在矩形受照面均匀性的要求，设计具有高均匀效果的自由曲面透镜。将水平角度φ等间距逐渐增加到90°，使用Runge-Kutta算法求解关于夹角θ的一阶偏微分方程，得到自由曲面透镜数据，并对数据进行曲面拟合，从而构建透镜三维模型。通过改变ρ值得到多组离散点数据，将各组离散点数据分别进行三维重构，得到不同大小的自由曲面透镜模型。通过自由曲面透镜模型的光学仿真分析得出，透镜效果最佳时，矢径ρ为32 mm，其均匀度可达到88.3%。设计方法适用于基于点列阵光源的自由曲面透镜设计，对LCD光固化3D打印技术高均匀度照明要求场合的透镜设计具有重要借鉴意义。