小纪汗煤样在塑性流动下力学性质试验研究

尤文强，郭静那，王光辉

（1.神东煤炭集团上湾煤矿，内蒙古鄂尔多斯 017209；2.中国矿业大学力学与土木工程学院，江苏徐州 221000）

岩石是1 种典型的脆性材料，在单轴压缩试验的典型曲线上，没有明显的屈服平台和残余强度。随着煤矿开采深度的增大，围压对煤岩的脆塑性的影响受到越来越多的关注[1-4]。此外，在富含水的地质赋存环境中，水的长时间作用也会改变的煤的脆塑性[5-6]。煤体的塑性体现在2 个方面，一是应力空间存在屈服面，二是峰后应力应变曲线形成滞环。应变曲线滞环比屈服面更容易观察，而且反映的信息更为丰富，也更容易进行定量化描述。

目前人们[7-8]通常根据单轴压缩试验和常规三轴压缩试验了解峰后岩石的塑性变形特性，考察黏聚力、内摩擦角、残余强度等力学参量的变化规律，也有部分学者[9-10]研究内变量（如塑性功）对后继强度的影响。对于循环加载下滞回性质的研究，主要分为单轴[11-14]和三轴[15-19]循环加卸载2 大类。一方面，学者们主要关注的是滞环的形状和面积，尚未对滞环的几何特征进行定量描述，由于岩样具有3个主应力和3 个主应变，故在一般情况下应讨论9条应力应变滞环的特征及变化规律，因此，仅讨论轴向应力-轴向应变滞环是远远不够的；另一方面，学者们主要是通过对煤岩峰前循环加卸载来研究塑性流动的变形，对剪切屈服后不同应力路径下的加卸载行为以及多重滞环下的滞环特征研究很罕见，对于煤层为主含水层这一特殊地质条件下塑性力学行为研究更为罕见。

一般说来，煤层的渗透率与应变分量存在某种程度的联系。因此，研究塑性流动下煤的变形规律有利于掌握小纪汗煤层渗透性变化规律。为了预防小纪汗主含水煤层突水事故，实现保水开采，利用MTS815 岩石力学试验系统的多用途程序编辑器试验实现峰后应力应变滞环的编程，卸载采用载荷控制、加载采用位移控制，得到不同围压下的轴向应变-轴向应力、径向应变-轴向应力和体积应变-平均正应力滞回曲线。利用滞回曲线的割线模量、宽长比减小及相邻滞环轴向峰值应力的比值3 个指标刻划滞回曲线的特征，进而说明围压和循环加卸载次数对煤样塑性变形的影响。

1 试验材料和试验方法

1.1 试验材料和试验系统

试验主要目的是认识剪切屈服后煤层为主含水层的滞回曲线特征，试样取自小纪汗煤矿2#煤层。煤样的直径d=50 mm，高度h=50 mm。

三轴滞环回试验采用MTS815.02 型岩石力学测试系统。试验原理以及油泵的结构原理如图1。步骤如下：①用热缩塑膜包裹在试样上，之后用电工胶带缠绕3 圈；②将煤样放入三轴压力室后，施加0.5 kN 的轴向载荷，再将环向引申计卡在试样的中间，关闭三轴室；③打开阀门S2、S3 和S6，关闭阀门S1、S4 和S5，随后注油，施加围压；④按照试验方案进行三轴滞后试验。

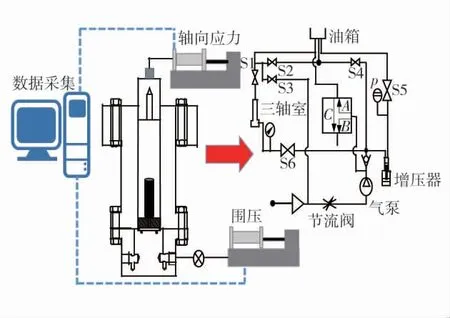
图1 试验原理图Fig.1 Test principle diagram

1.2 试验方案

为了研究剪切屈服后煤柱塑性状态下的变形规律，首先对试样进行常规三轴压缩试验，使其达到塑性区状态。由于煤样的离散性很大，因此取每块煤样峰后某点A*做为塑性区的起始应力状态点，控制状态点A*的轴向应力为峰值应力的60%～90%，此状态点越接近峰值，塑性流动下压力的滞后性更加丰满，得到塑性区煤柱的变形规律越全面。但如果太接近峰值，煤样可能会被压碎，从而导致整个实验失败，因此一般取每个煤样峰后阶段峰值应力的70%作为塑性区的初始值。试验方案如图2。

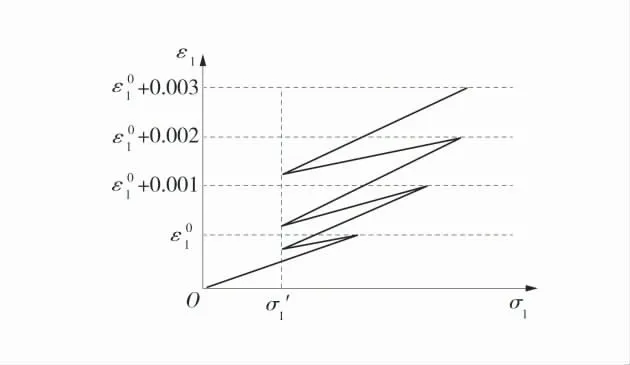
图2 试验方案图Fig.2 Test plan diagram

1）围压达到设定值后，以轴向应变控制模式，加载速率为0.003 mm/s，加载至峰后峰值应力的70%A0（σ10=70%，σmax，ε10）状态，对应于图2 中的ε10所处的虚线与加载曲线的交点位置。

2）围压保持不变，调至轴向应力控制模式，以0.5 MPa/s 的速率将轴向载荷卸载至2 kN，对应于图2中的σ1′。

3）再次将MTS815 控制模块调至轴向应变控制模式，以0.003 mm/s 的速率加载至ε10+0.001，由此形成1 条闭合的滞环。

4）然后再以同样的方式进行加卸载，每次卸载均降至2 kN（σ1′），每次加载的最大轴向应变均比上一次增加0.001，具体应力路径如图2（σ1为轴向应力，ε1o 轴向应变）。根据小纪汗煤层的地质背景情况[20-21]，围压设定4 级，分别为2.0、4.0、6.0、8.0 MPa。

1.3 塑性流动下煤的滞回性试验原理

通过上节的试验方案可以得到3 种应力应变滞回曲线，分别为轴向应变-轴向应力（ε1-σ1）、径向应变-轴向应力（ε3-σ1）和体积应变-平均正应力（εvσm）滞回曲线。体积应变和平均正应力是轴向和径向应力应变的综合反映，在岩石力学中，正应力、正应变均规定以压为正，体积应变和平均正应力按以下公式计算：

式中：ε1、ε3为轴向应变、径向应变；σ1、σ3为轴向应力、径向应力；σm为平均正应力。

一般不同应力循环下得到的应力应变滞环如图3，为了描述该滞环的几何特征，定义了割线模量、宽长比、峰值应力比3 个参量[22]。

图3 典型的应变-应力滞环Fig.3 Typical strain-stress hysteresis

1.3.1 割线模量Kh

图3 中滞环最左端点和最右端点所在直线的斜率定义为割线模量。这个参量与塑性应变的大小呈正比。在图3 中，最右点A 的坐标为（x1，y1），最左点B 的坐标为（x2，y2），因此：

式中：Kh为每个滞环的割线模量。

1.3.2 宽长比η

滞环的宽长比反映了应力、应变滞后性的强弱，该参数与滞后性呈正相关，滞后性越强，表明煤岩的塑性越强。滞后性越弱，即宽长比趋于0 时，加卸载时的应力应变曲线基本一致，没有形成滞环，表明煤岩的弹性越强。

式中：η 为每个滞环的宽长比；l 为滞环曲线的长度；d 为滞环曲线的宽度。

1.3.3 峰值应力比

每个环的峰值应力比反映了煤的应变软化程度，峰值应力比越大，软化越明显。众所周知，电和磁的滞环曲线均是重复的，即加载和卸载时的滞环完全重合。但是煤岩材料的应力-应变滞环不重合。因此，需要考虑每个闭环之间大小和位置的差异。煤岩体材料的滞回模型主要分为2 个方面，滞回规则和骨架曲线。为了了解骨架曲线的概念，给出了包含3 个滞环的应力-应变曲线，含有3 个闭环的ε1-σ1曲线如图4。由此引入峰值应力比。

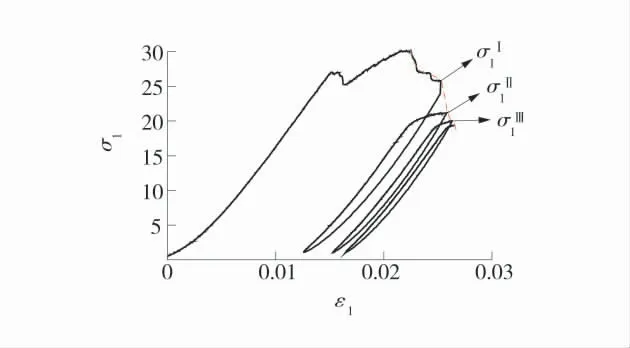
图4 含有3 个闭环的ε1-σ1 曲线Fig.4 ε1-σ1 curve with three closed loops

峰值应力比定义为相邻2 个滞环间峰值应力比值的几何平均值。3 个滞环的轴向峰值应力依次记作σ1Ⅰ、σ1Ⅱ和σ1Ⅲ，则峰值应力比为：

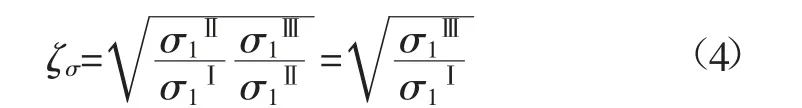
式中：ζσ为轴向应力峰值比。

2 剪切屈服后煤样加/卸载应力路径下力学性质

2.1 加/卸载应力路径下应力-应变滞回曲线

轴向应变-轴向应力和径向应变-轴向应力滞回曲线如图5～图8。

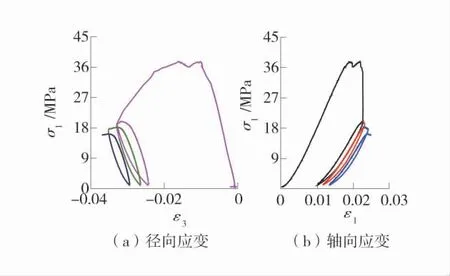
图5 σ3=2 MPa 下ε1-σ1 和ε3-σ1 滞回曲线Fig.5 Hysteresis curves of ε1-σ1 and ε3-σ1 under σ3=2 MPa

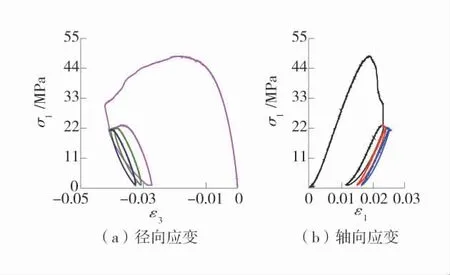
图6 σ3=4 MPa 下ε1-σ1 和ε3-σ1 滞回曲线Fig.6 Hysteresis curves of ε1-σ1 and ε3-σ1 under σ3=4 MPa

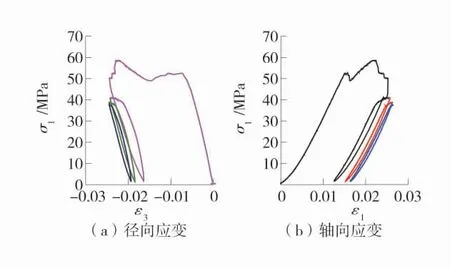
图7 σ3=6 MPa 下ε1-σ1 和ε3-σ1 滞回曲线Fig.7 Hysteresis curves of ε1-σ1 and ε3-σ1 under σ3=6 MPa

由图5～图8 可知，煤样轴向应变-轴向应力和径向应变-轴向应力滞回曲线具有以下特点。

1）全应力-应变曲线在峰值后有所陡降，塑性区比较明显，峰值附近不断波动，没有表现出明显的脆性行为。

2）第1 次循环加卸载形成的滞环比较丰满，随着循环次数的增多，滞环形状变尖锐，近似成凸镜形。

3）在围压等于2.0 MPa 条件下，轴向应变-轴向应力滞环割线模量小于弹模。随着围压的增大，逐渐趋于相同。此外，在围压等于2.0 MPa 和6.0 MPa 的条件下，曲线的3 个滞环向左移动。在围压等于4.0 MPa 和8.0 MPa 条件下，第1 个滞环将后2 个包围。

4）随着应力不断循环，滞环的面积减小。滞回曲线的面积表示应力循环所消耗的能量，能量消耗是由于煤样中微裂隙的扩展、新裂隙的生成以及颗粒间摩擦生热的损耗导致。滞环面积的缩小表明消耗的能量在减小。

不同围压下的体积应变-平均正应力滞回曲线如图9。

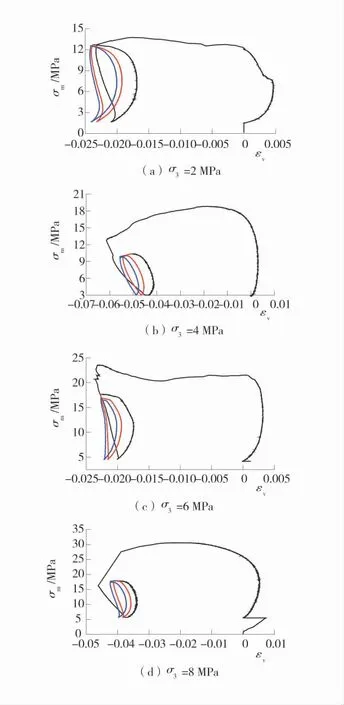
图9 不同围压下εv-σm 滞回曲线Fig.9 Hysteresis curves of εv-σm under different confining pressures

由图9 可以看出，在同一围压下，3 个滞环依次向左移动，并且有重叠的部分，第1 个滞环的面积明显大于第2、第3 个滞环，第2、第3 个滞环的割线模量、面积和形状基本相同。围压2 MPa 和4 MPa 时，3 个滞环左下端尖锐右上端饱满。围压6 MPa 和8 MPa 时，两端均比较饱满。

2.2 应力-应变滞回曲线的几何特征

通过分析滞环的割线模量、宽长比和峰值应力比3 个参量随围压以及循环加卸载次数的变化规律，来描述滞回曲线的几何特征。

2.2.1 割线模量特征

不同围压下轴向应变-轴向应力和径向应变-轴向应力滞回曲线中割线模量见表1～表2，不同围压下各滞环的割线模量如图10。

表1 ε1-σ1 滞回曲线的割线模量Table 1 Secant modulus of ε1-σ1 hysteresis curve

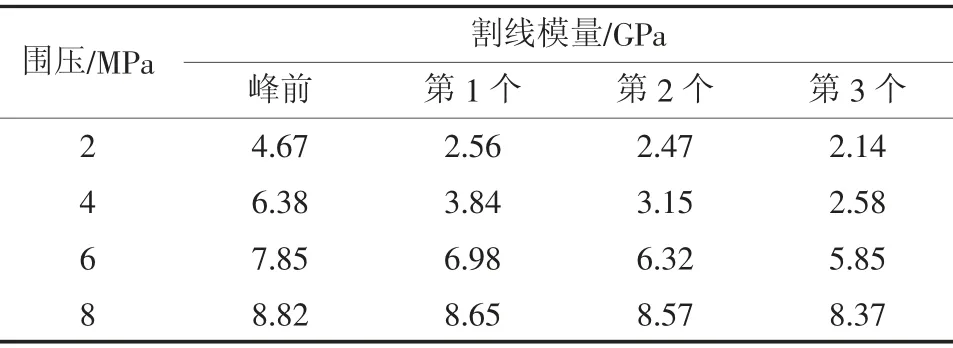
表2 ε3-σ1 滞回曲线的割线模量Table 2 Secant modulus of ε3-σ1 hysteresis curve

结合表1 和表2，滞环的宽长比如图10 可知，不论是轴向应变-轴向应力还是径向应变-轴向应力滞回曲线，煤样的弹模大于峰后的割线模量，并且随着循环次数的增多，割线模量变小，表明循环次数越多煤样产生的塑性应变增量有所降低。随着围压的增大，2 种曲线不论是峰前还是峰后应力循环过程中，割线模量随之增大，表明随围压的增大，煤样塑性增强。

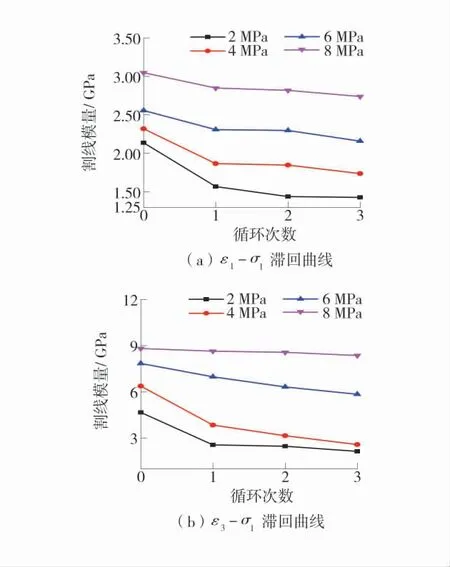
图10 不同围压下各滞环的割线模量曲线Fig.10 Secant modulus of each hysteresis under different confining pressures

2.2.2 滞环宽长比特征

不同围压下轴向应变-轴向应力、径向应变-轴向应力和体积应变-平均正应力滞回曲线各滞环的宽长比见表3～表5，不同围压下峰值应力比曲线如图11。

结合表3-表5 和图11 可以看出，随着应力不断地循环，滞回曲线的宽长比大致呈降低趋势，表明煤样应力应变曲线的滞后性变弱，进而可以说明煤样的塑性变形增量降低。

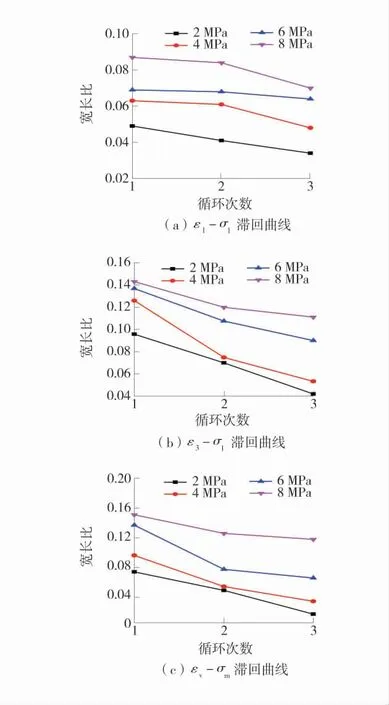
图11 滞环的宽长比Fig.11 Width to length ratio of hysteresis

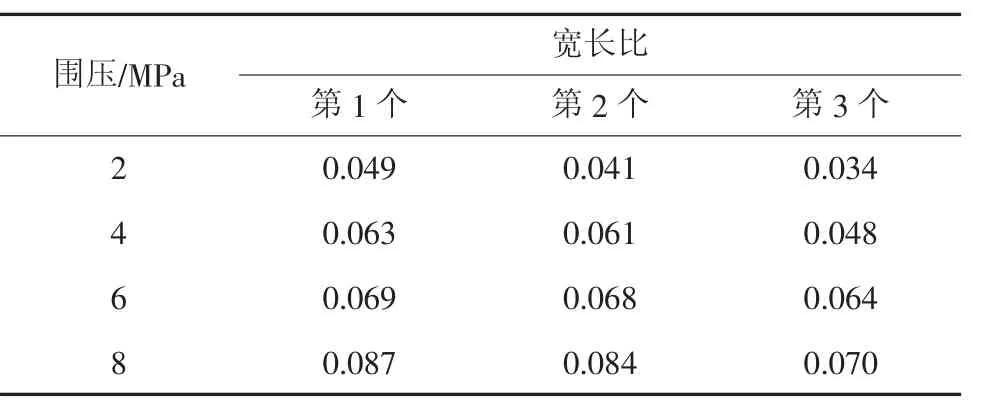
表3 ε1-σ1 曲线中各滞环的宽长比Table 3 The width to length ratio of each hysteresis loop in the ε1-σ1 hysteresis curve

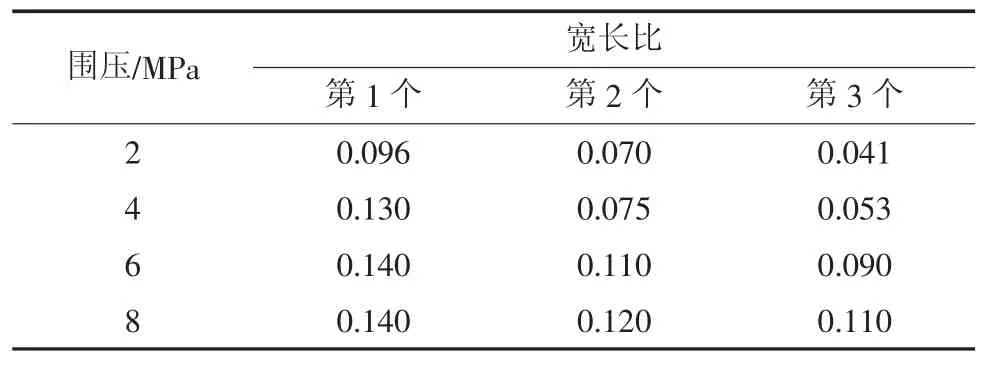
表4 ε3-σ1 曲线中各滞环的宽长比Table 4 The width to length ratio of each hysteresis loop in the ε3-σ1 hysteresis curve

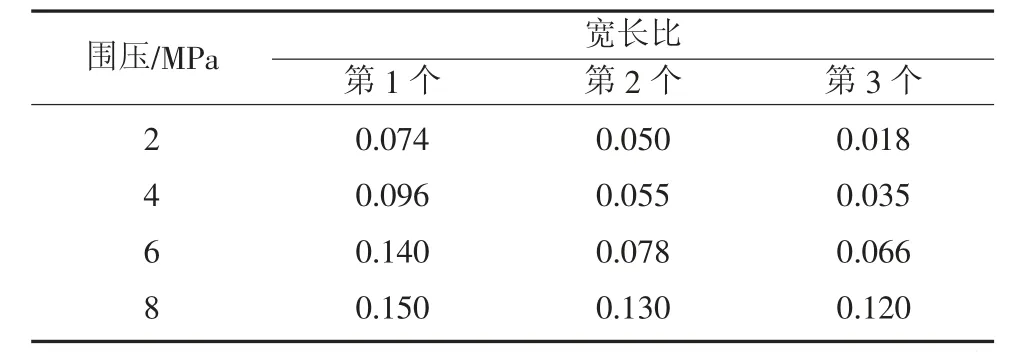
表5 εv-σm 曲线中各滞环的宽长比Table 5 The width to length ratio of each hysteresis loop in the εv-σm hysteresis curve

随着围压的增大，滞回曲线的宽长比增大。再次表明随着围压的增大，煤样产生的塑性变形增量增大，有更多的能量提供给新裂隙生成，煤样的塑性得到增强。

2.2.3 峰值应力比特征

不同围压轴向应变-轴向应力滞回曲线各滞环的峰值应力比见表6，不同围压下峰值应力比曲线如图12。

表6 不同围压下ε1-σ1 滞回曲线中的应力峰值比Table 6 The stress peak ratio in the hysteresis curve of ε1-σ1 under different confining pressures

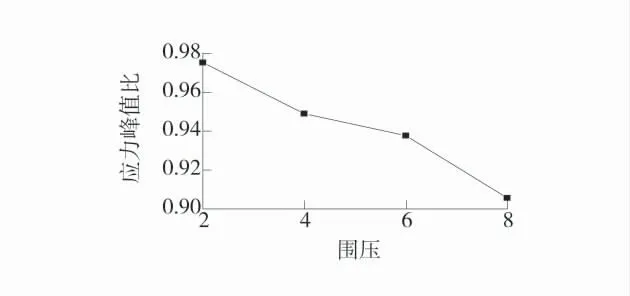
图12 不同围压下峰值应力比曲线Fig.12 Peak stress ratio curve under different confining pressures

由图12 可知，围压由2 MPa 升高至6 MPa，峰值应力比由0.98 降至0.91。表明随着围压的增大，峰值应力比减小，滞环的间隔变小，表明应力得到了强化。再次表明随着围压的增大，煤产生的塑性变形增量变大，煤的软化效应增强。

2.3 应力强度分析

根据第二强度理论，对于材料内一点，其最大伸长应变ε1达到单向拉伸断裂的极限值εu时，材料就发生断裂破坏，数学表达式为：

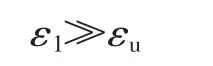
利用广义胡克定律以应力表示的破坏条件为：

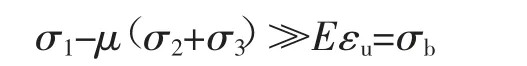
式中：σ1为轴压；σ2为第二应力；σ3为围压；E为杨氏模量和泊松比；σb为拉伸断裂应力。显然随着围压增大，应力强度σb提高，但是卸载后再加载达到极限应变εu时却未发生破坏，这说明第二强度理论不适用于峰后破坏判断。随着循环次数的增加，塑性应变不断增加，此时发生破坏的极限值应变εu提高，峰值应力σ1逐渐减小。结合前一节中刻画滞回曲线的3 个参数分析可知：在循环载荷作用下，煤样塑性应变累积，韧性增强，由脆性材料向塑性材料过渡。

3 结 论

1）得到了煤样在峰前全应力-应变曲线以及不同应力路径下轴向应变-轴向应力、径向应变-轴向应力和体积应变-平均正应力3 种滞回曲线。全应力应变曲线在峰值处会出现波动随后产生陡降，滞环形状近似凸镜形。

2）随着应力循环次数的增多，轴向应变-轴向应力和径向应变-轴向应力滞回曲线中割线模量、宽长比变小。表明随着加卸载次数的增多，滞后性减弱，煤样的塑性行为减弱。

3）随着围压的增大，滞回曲线割线模量和宽长比变大，峰值应力比减小，表明围压越大煤样产生的塑性变形增量越大，煤样的软化效应增强。