基于信息增益的高维数据的异常检测算法

陈 晓，阎少宏，葛子轩，史冰冰

(1. 华北理工大学 理学院，河北 唐山 063210；2. 河北省数据科学与应用重点实验室，河北 唐山 063210；3. 唐山市数据科学重点实验室，河北 唐山 063210；4. 华北理工大学 电气工程学院，河北 唐山 063210；5. 华北理工大学 人工智能学院，河北 唐山 063210)

0 引言

异常存在于各个领域，比正常携带的信息更多也更为重要，这些信息可能是灾难性后果的预警或者标志，及时检测出异常尤为重要[1]。随着信息技术和网络技术的发展，数据集变得更加庞大，结构更加复杂，空间维度更高。这些问题导致异常检测的难度越来越大，同时也会带来召回率跟精确率下降的问题。文献[2]提出一种基于偏最小二乘（PLS）法和核向量机（CVM）组合式的异常入侵检测方法。文献[3]提出基于 KNN的累积距离的异常检测方法。文献[4]提出基于熵和改进的 SVM 多分类器的异常流量检测方法。文献[5]提出了一种基于迭代随机采样策略的排序算法。文献[6]提出一种信息熵加权的异常检测方法。上述算法大多应用于数据维度较小的数据集中，但是随着维度的不断增加，高维数据的异常检测会有精确率跟召回率下降的问题。针对高维属性对异常检测带来的维数灾难问题，本文提出一种结合信息增益方法和 Top-k算法的异常检测方法。

1 相关知识

1.1 聚类算法

聚类算法是一种无监督学习的典型算法，通常在异常检测中异常类数据较少甚至没有，因此不能直接借用监督型学习方法[7]。无监督异常检测方法因其简单、高效的特点，被广泛用于大数据中的异常检测[8]。其中应用最广泛的是K-means聚类，但是K-means算法存在几个问题：一是中心初始位置选择不好会导致迭代次数增多和计算量增大，严重影响聚类效果。二是并未考虑数据中不同属性之间的差异，不同属性的信息增益占比不均衡。针对以上出现的问题，本文提出改进的聚类算法，通过肘部法则选择最佳的聚类数，通过 1.2的方法确定初始聚类中心，替代原有的随机选择方法。

1.2 初始聚类中心的确定

传统K-means算法的初始聚类中心是随机生成的，如果初始聚类中心选择不好，会导致聚类迭代次数的增多和计算量的增大[9]。为了消除这种影响，在初始数据集中选取两点直径距离尽量远的点构成K个初始聚类中心，并依此完成改进的K-means算法，一定程度消除了以上因素的影响。具体算法流程如下：

输入：样本集M，初始聚类中心个数K，聚类中心{}；

Step.1计算样本集M中的平均值，将此平均值设为样本中心C；

Step.2计算样本集M中的每个点到样本中心C的距离，选择离样本中心最远的那个点C1作为第一个初始聚类中心，此时聚类中心为{C1}；

Step.3计算剩余的M-1个点到C1点的距离，选取最远的那个点C2，加入初始聚类中心，此时聚类中心为

Step.4重复Step.2-Step.3步直到找到K个初始聚类中心

1.3 信息增益

针对高维数据对异常检测的检测率和检测时间产生不利影响的问题。通过对数据降维保留信息增益占比较大的属性，更有利于提高异常检测的准确率，信息增益的计算公式如下：

（1）信息熵的计算：

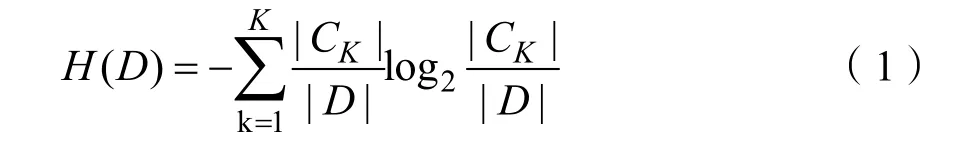
其中训练数据集总个数为|D|，某个分类的个数为|CK|。

（2）选定A的条件熵计算：

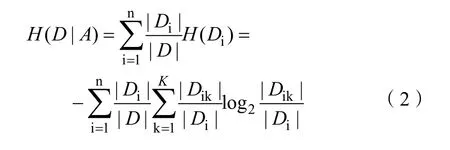
其中|Di|为选定特征的某个分类的样本个数，交集|Dik|可以理解在Di条件下某个分类的样本个数。

（3）信息增益的计算：

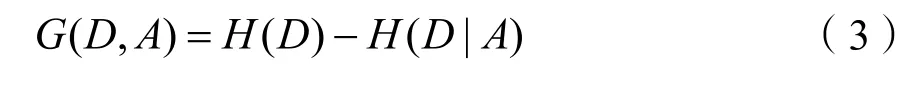
信息增益越大表示该属性对数据的影响越大，在进行数据分析时应该重点考虑。

2 基于信息增益的异常检测算法

算法步骤

Step.1计算每个属性的信息增益，用 Top-k算法选择信息增益排名的前K个属性，对其他属性进行裁剪；

Step.2利用肘部法则，对数据集确定合适的初始聚类数；

Step.3利用本文1.2改进后的初始聚类中心的选择办法，选择合适的初始聚类中心；

Step.4在 K-means聚类算法中引入 Step.2、Step.3方法，将数据集聚成M类；

Step.5计算每个簇中的平均距离，以及各个点到聚类中心的距离，如果点到聚类中心的距离大于平均距离，就把该点作为异常点；

Step.6对数据集中的数据取不同的前K个属性再次重复Step.1～Step.4。

3 实验分析

3.1 实验设计与结果分析

实验运用本文 1.2的方法确定初始聚类中心后运用K-means算法进行聚类，通过欧式距离计算每个点到簇中心距离，如果大于平均距离就把该点定为异常点，实验结果显示改进的 K-means聚类后得异常点个数为289。

运用相同的数据集，加入了加权信息熵的方法后进行聚类，异常点的个数为 288。可以看出加权信息熵的办法在高维数据中的异常检测效果并不理想，在加权信息熵的基础上进一步计算每个维度的信息增益，并进行排序。分别取前10、20、30、40、50、60、70、80、90 维数据重新进行聚类，计算每一次聚类结束后的异常点的个数，分别求出异常点的个数为337、341、331、269、276、259、264、260、262。异常点的个数如图1所示。

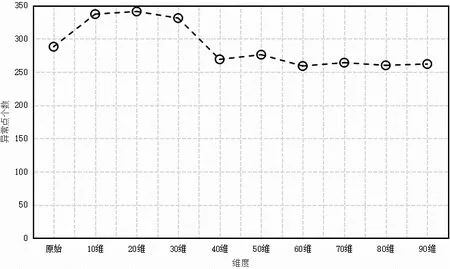
图1 取前M维信息增益的异常点的个数图Fig.1 shows the number of outliers with the first m-dimensional information gain

基于加权信息熵聚类的过程中，当迭代次数为 10时异常点的个数趋于稳定，取信息增益前10、20、30、40、50、60、70、80、90 维数据进行聚类的过程中，迭代次数分别为16、10、10、9、11、16、20、20、16。可以看出在加权信息熵的基础上运用信息增益取前K个属性的方法同样也会增加异常点的个数，说明本算法对高维数据异常点的检测效率有所提高。将召回率和精确率作为异常检测性能的评价指标。本文所提的算法（前20维）与加权信息熵的算法进行比较，如表1所示，在异常点个数增多的前提下，召回率跟精确率也有一定的提高。

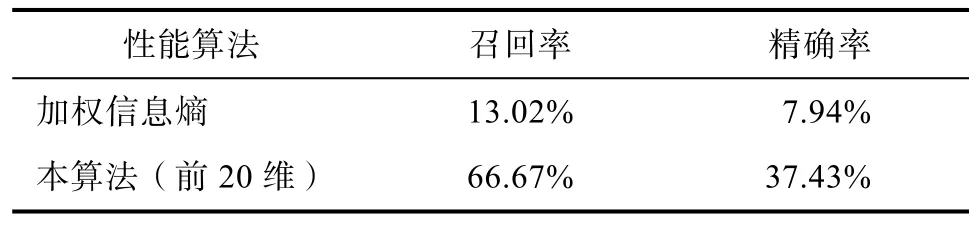
表1 两种算法在数据集中的实验对比结果Tab.1 experimental results of two algorithms in datasets

3.2 实验小结

实验结果表明与加权信息熵的异常检测算法相比，本文提出的改进算法的召回率和精确率分别提高 53.65%和 29.49%，在异常点个数的检测上也有明显的提高。究其原因如下：首先，改进算法引入了信息增益的概念，根据各属性影响程度的不同，计算出影响异常点检测中每个属性的信息增益；其次改进算法选择了更优的初始中心，在迭代过程中数据对象的异常度计算与其所属的簇中心相关。从而使得异常计算的结果更加准确，提高了异常检测的性能。

4 结论

本文根据异常检测以及聚类的特点在基于信息熵异常检测算法基础上改进了结合信息增益和Top-k的异常算法，通过计算数据每个属性的信息增益，取前K个属性，忽略掉非重要属性重新进行聚类，有效的避免了其他属性对异常检测的影响，异常检测的效果更优。实验结果表明异常点的检出个数比加权的信息增益算法明显增多，取得了明显的效果。但是本算法对非数值型数据的处理较差，如何进一步提升算法效率、处理多种数据类型以及设计不确定性异常的检测方法是未来的研究重点。