标的资产带有红利支付的脆弱期权定价问题研究*
李 钰,石学芹,吕会影
(1.安徽机电职业技术学院公共基础教学部,安徽 芜湖 241000;2.安徽工程大学数理学院,安徽 芜湖 241000)
引言
Johnson和Stulz[1]首次在期权定价问题中考虑交易对手违约的信用风险,并将该期权命名为脆弱期权.近年来国内外学者对于该问题展开了一系列的讨论.Johnson和Stulz[1]与Hull和White’s[2]分别从结构化模型和约化模型两个不同的角度来探讨脆弱期权定价问题.而Klein[3]在研究过程中将信用风险与标的资产价值联系到一起,将前述的研究结果进行了进一步的推广,建立起更符合实际情形的定价模型.国内学者魏正元和高红霞[4]、刘桂芳[5]、王之渊和陈萍[6]以及张二姚[7]均在文献[3]的基础上从不同的角度探讨了跳扩散过程下的脆弱期权定价问题,由实际交易可知,红利支付对于期权定价有着直接的影响.为了导出更具有实际市场价值的脆弱期权定价公式,文中将利用等价鞅测度方法推导出考虑红利支付的欧式看涨脆弱期权定价模型.
1 模型描述
本文讨论的内容为欧式脆弱期权定价问题,涉及的资产定价模型为期权标的资产价格方程和期权卖方资产价格方程,具体如下所示:
dSt=μStdt+σ1StdW1t, dVt=bVtdt+σ2VtdW2t
式中μ和σ1为股票价格的常值期望收益率和波动率,b和σ2为期权卖方资产价格的常值期望收益率和波动率,Wit(i=1,2)均为标准布朗运动,且Cov(dW1t,dW2t)=ρdt.

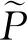
利用伊藤公式,可以得到上述方程的解为:
(1)
(2)
在风险中性市场中,(lnST,lnVT)满足二维正态分布:
2 脆弱欧式期权定价
定理1在上述假设之下,欧式脆弱看涨期权价格为:
C(t,T)=StN2(a1,a2,ρ)-Ke-(r-q)(T-t)N2(b1,b2,ρ)+
其中

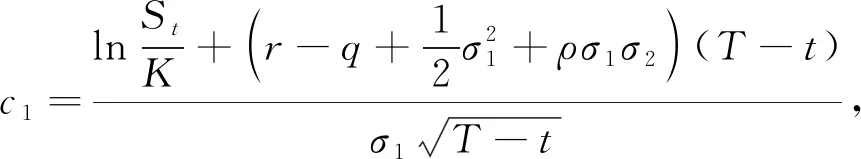
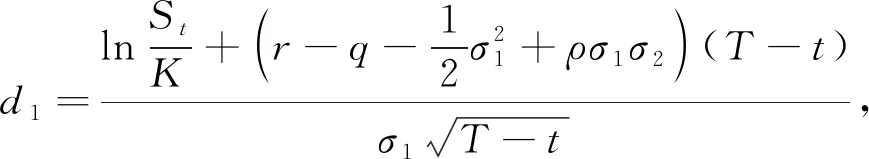
证明为了简化整个计算过程,将C(t,T)拆分成4个部分.即
C(t,T)=e-(r-q)(T-t)[A1-A2+A3-A4].
其中:

1)A1的计算过程

将上式代入A1中可得:
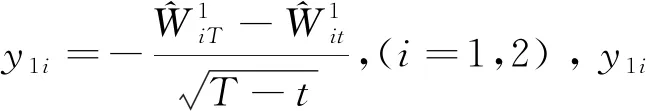
所以,A1=Ste(r-q)(T-t)N2(a1,a2,ρ),其中
2)A2的计算过程
由于K是常数,不用做等价测度变换,从而直接可得A2=KN2(b1,b2,ρ),其中
3)A3的计算过程
从而
将上式代入A3中可得:

式中
4)A4的计算过程

3 数值分析
为了更加直观地体现出红利对于欧式脆弱看涨期权定价的影响,本文将基于以下参数值,并借助于MATLAB软件计算出相应的期权价格.
具体参数值为:St=40,Vt=40,D=8,D*=8,K=35,r=0.05,ρ=0.5
σ1=σ2=0.3,T-t=1.
从表1数据中可以看出:在其他参数不变的前提下,当γ越大时期权价格会越低;同时在其他参数不变的前提下,当q越大时期权价格也会相应降低,这些结论都与实际情况相吻合.当γ越大即交易对手发生违约的可能性会提高,那么脆弱期权价格自然会降低.当q越大即红利支付率越高时,会使股票价格降低,从而导致欧式看涨脆弱期权的价格也随之降低.
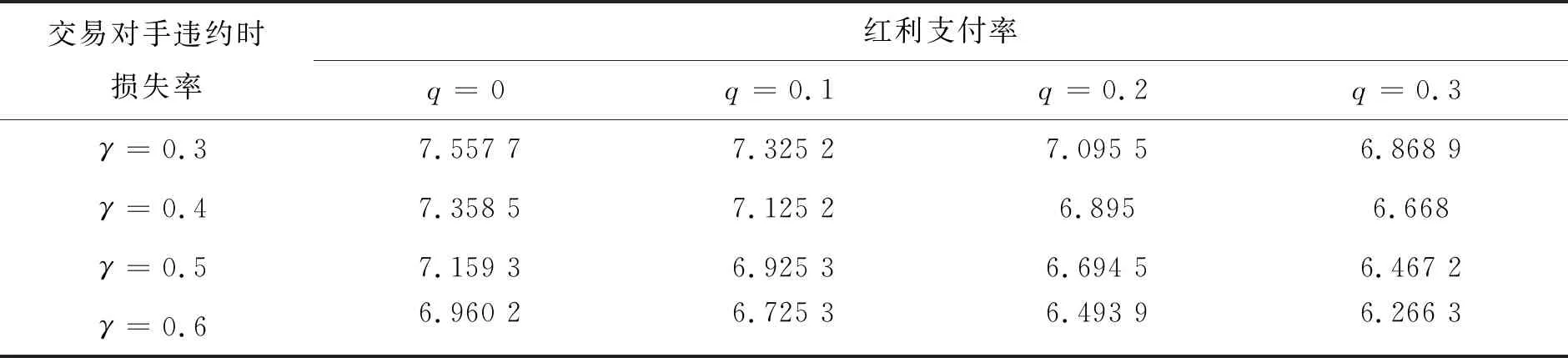
表1 不同红利支付率和交易对手违约损失率下的脆弱期权价格

