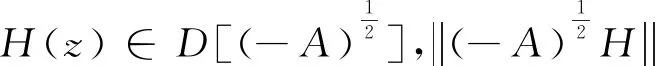带有非局部条件半线性中立型测度方程的可控性*
刘文杰
(安徽城市管理职业学院公共教学部,安徽 合肥 230011)
引言
假设(X,‖·‖)是一个Banach空间,A:D(A)⊆X→X是C0半群{T(t),t≥0}无穷小生成元,J∈[0,b],b>0,U是一个Banach空间,L2(J,U)是一个允许控制函数的Banach空间,算子B:U→X是有界的线性算子,记号C(J,X)表示从J到X上全体连续函数构成的空间,G(J,X)为J上的正则函数空间.
考虑如下带有非局部条件的半线性中立型测度方程:
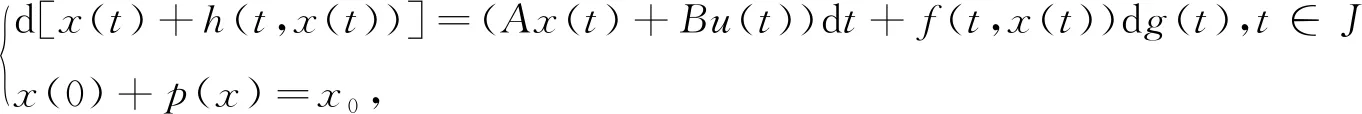
(1)
其中变量x(·)在Banach空间X上取值,g:J→R不减的左连续函数,f,h:J×X→X,控制函数u∈L2(J,U),p:C(J,X)→X后面给出定义.
测度方程由Das[1]提出并研究,在许多应用数学领域都有应用,如控制论、博弈论、物理学等[2-4].众所周知,常微分方程描述的系统受到扰动时,扰动是连续或可积的,则扰动后的系统仍是常微分方程;若扰动是脉冲型的,扰动后的系统就成为测度方程.测度方程涵盖了一些常见的方程模型,如:常微分方程、差分方程、脉冲微分方程.在最优控制问题中,若控制函数u(t)是脉冲型的,控制系统会产生瞬动性态,描述这样的系统,就要用测度方程.更多关于测度方程的介绍见文献[5].近年来,许多学者研究Banach空间中具有非局部条件的微分积分方程可控性问题[6-8].如:申明圆[6]等人利用分数阶紧算子理论和Kuratowski不动点定理讨论带有非局部条件的分数阶中立型微分系统近似可控性.杜珺[7]等人应用非紧测度性质和不动点理论,给出一类具有无穷时滞非局部条件下分数阶中立型积分微分演化系统可控性的充分条件.受到上述启发,文章在强连续半群非紧的条件下,通过将可控问题转化为积分算子不动点问题,使用Kuratowski非紧性测度估计及不动点定理讨论带有非局部条件的半线性中立型测度方程的可控性.
1 预备知识
回顾一些相应的概念及正则函数空间中Kuratowski非紧性测度的若干性质.
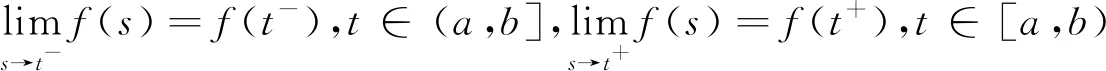

h(t+)=h(t)+f(t)Δ+g(t),t∈[a,b),h(t-)=h(t)-f(t)Δ-g(t),t∈(a,b]
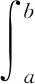
定义2[4]一个集合A⊂G([a,b],X)称为等度正则的,当且仅当∀ε>0,t0∈[a,b],存在δ>0,使得:
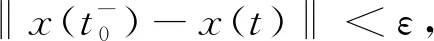
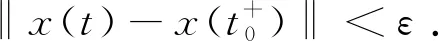
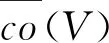
定义3 函数x∈G(J,X)被称为方程(1)的温和解,若x(0)+p(x)=x0成立,且满足如下测度积分方程:
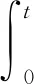
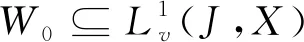
定义4 若∀x0,x1∈X,存在控制函数u∈L2(J,U),使方程(1)的解满足x(b)+p(x)=x1,则方程(1)称为在J上非局部可控.
引理4[10]设X是Banach空间,D是X中的有界集,存在D的可数子集D0⊂D,使得α(D)≤2α(D0).
引理5[6]设Ω是Banach空间X上的闭凸非空集合,P,Q的映射是从Ω→X,且满足:
1)Px+Qy∈Ω(∀x,y∈Ω),2)P是压缩映射,3)Q是紧的和连续的,则Px+Qx=x存在一个不动点在Ω中.
2 主要结论
讨论带有非局部条件半线性中立型测度方程的可控性,为方便叙述,假设如下:

(H2)若∀x∈G(J,X),函数f(·,x(·))∈LSg(J,X),且映射x→f(·,x(·))从G(J,X)到LSg(J,X)是连续的.
(H3)存在函数φ∈LSg(J,R+)和一个非减的连续函数φ:R+→R+使得‖f(t,x(t))‖≤
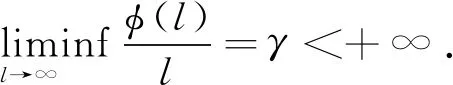
(H4)在函数m∈LSg(J,R+),对于任意的有界集合B⊂X,得α(f(t,B))≤m(t)α(B).
(H5)p,h:G(J,X)→X连续且紧,存在正常数G1>0,使得‖p(x)‖≤G1,∀x∈G(J,X).
(H6)存在常数c1,c2,Lh,使得(-A)βh(t,x)连续且满足:
‖(-A)βh(t,x)‖≤c1‖x‖+c2,‖(-A)βh(t,φ)-(-A)βh(t,φ)‖≤Lh‖φ-φ‖.
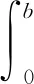
(h′)W的逆算子W-1存在,它取值于L2(J,U)/kerW,且存在常数M2,M3,使得‖B‖≤M2,
‖W-1‖≤M3.
(h″)存在Kw∈L1(J,R+),对任意有界集合Q⊂X,有:α((W-1Q)(t))≤Kw(t)α(Q(t)).
定理1假设(H1)~(H7)成立,记:
M0=‖(-A)-β‖,
M=‖x1‖+G1(1+M1)+M1(‖x0‖+M0(c1(‖x(0)‖+‖x(b)‖)+c2))+
则系统(1)在J上非局部可控.
证明通过(H7),对任意的函数x(·),定义控制函数:
u=W-1{x1-p(x)-T(b)[x0+h(0,x(0))-p(x)]+h(b,x(b))+
定义算子Γ:G(J,X)→G(J,X)
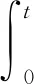
若可以证明Γ有一个不动点,则该不动点就是方程(1)的解.显然,Γ(x)(b)=x1-p(x),即指明控制函数u(·)将方程(1)从初始状态控制到时刻b的状态.
设l>0,Bl={x∈G(J,X):‖x‖∞≤l},Bl是有界闭凸集,记:Γ(Bl)={Γ(x):x∈Bl}.
步骤1:一定存在一个正数l>0,使得Γ(Bl)⊆Bl.反之,则存在一个函数xl∈Bl,使得Γ(xl)∉Bl,即Γ(xl)(t)>l,于是
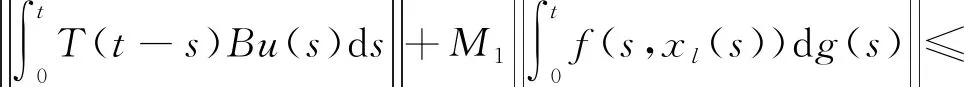
不等式两边同时除以l,并取l→+∞时的极限,得出:
这与假设条件矛盾.因此,一定存在一个正数l>0,使得N(Bl)⊆Bl.
设Γ=Γ1+Γ2,其中Γ1,Γ2分别定义为如下形式:
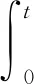
接下来,证明算子Γ1是压缩的,Γ2是紧算子.
步骤2:证明算子Γ1是压缩的,对任意的x,y∈Bl,由条件(H6)及假设条件可知
‖Γ1(x)(t)-Γ1(y)(t)‖≤‖T(t)(-A)α(-A)-α(h(0,x(0))-h(0,y(0)))‖+
因此,得出算子Γ1是压缩的.
步骤3:为证明算子Γ2是紧的.首先证明Γ2是连续的.设{xn,n∈N+}∈Bl,且xn→x(n→∞),由(H5)(H6)和T(t)的有界性,对每一个t∈[0,a],当n→∞时,有
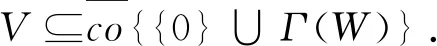
其中p(V)是相对紧的且T(t)是强连续算子,应用Arzela-Ascoli定理可知集{T(·)p(V):V⊆Bl}相对紧的,所以α(T(·)p(V))=0.而由条件(H1)~(H7)可推出:
从而得出:
故α(V(t))=0,t∈J.得出V是相对紧的,由引理5知Γ有一个不动点,即方程(1)是可控的.
3 例子
考虑以下带有有非局部条件的半线性测度方程:
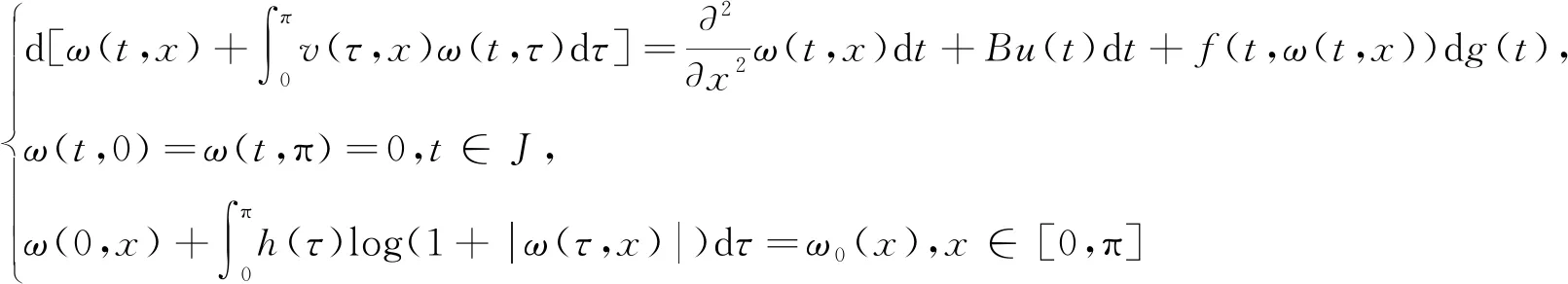
(2)
令X=L2([0,π]),v,k:[0,π]×[0,π]→R是连续函数,定义A:X→X,由Az=z″,并满足:
D(A)={z∈X:z绝对连续,z″∈X,z(0)=z(π)=0}
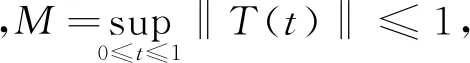
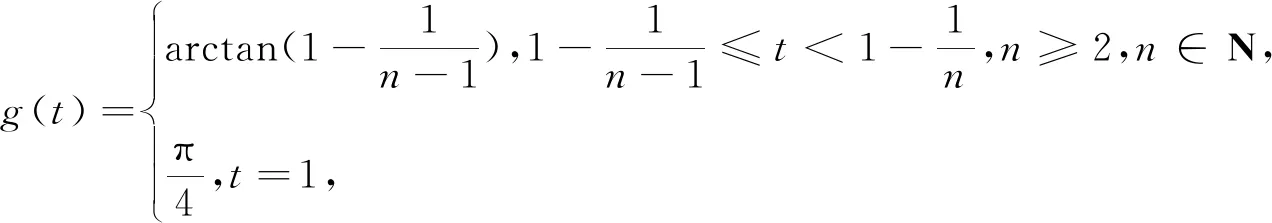
显然g:[0,1]→R是一个左连续不减函数.并假设以下条件成立:
(h1)函数v(τ,x)是可测的,v(τ,0)=v(τ,π)=0,且满足:
(h2)令F(t,ω(x))=f(t,ω)(x),t∈[0,1],x∈[0,π].F(t,ω(x))=2sin(ω(x)),则
(h3)对任意有界集D⊂X,有α(f(t,D))≤2α(D).
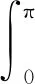
W-1∈L2(J,X)/kerW.