小波分析在地铁隧道安全监测中的应用

熊晓峰， 项 鑫

（1.河南省地球物理空间信息研究院，郑州 450009； 2.河南省地下空间探测信息工程技术研究中心，郑州 450009）

近年来，城市轨道交通发展迅猛，截至2020年年底，全国已有44个城市开通地铁，全国地铁运营里程达7 545.5 km，年度内运载客运量175.9亿人次，进站量109.1亿人次，地铁里程成为衡量城市发展程度的重要指标［1］. 地铁的修建一方面要考虑城市发展需要，同时也要考虑城市的财政收入，因为修建地铁需要高昂的投入和不菲的运营成本［2］. 地铁建成以后，受到地铁自身结构老化、地下工程开挖、周边工程建设、地面沉降等因素的影响［3-4］，会导致地铁隧道产生形变，形变超出一定量值会影响地铁结构安全［5］. 因此需要在地铁建设和运营维护过程中对地铁结构进行安全监测［6］，以准确获取地铁的变形状态和变形速率. 正常情况下，地铁沉降变化量小［7］，微小的变形量值不能够准确提取地铁的变形趋势，同时，观测过程产生的粗差和噪声会对地铁观测数据产生影响［8］，如何有效分析和处理地铁观测数据成为地铁安全监测的关键［9］. 小波分析是处理时间序列观测数据十分优异的数据处理模型［10-11］，被称为“数学显微镜”，将小波分析应用于地铁沉降观测具有理论和实际的可行性. 本文将小波分析应用于地铁沉降监测数据处理，以实际项目为依托，进行了工程应用，获取了有益的结果，研究内容为地铁变形监测提供了依据.

1 小波分析

1.1 小波分析理论

小波变换是傅里叶分析的发展与进阶，经过小波变换处理后的信号残差均匀地分布在正负两侧，并接近于0，因此称为小波. 小波变换的公式如下：

其中：φ表示小波；a为伸缩因子；τ 为平移因子；Ψ(w) 为φ(t)的傅里叶变换. 小波变换对大部分信号都能处理得很好. 对于小波变换，只要能够符合小波变换的性质、特点，都是可以根据已有信号来推导或构建形成小波基［12］. 这种处理的灵活性是其他任何一种数理变换都根本无法做到的. 小波变换对绝大部分信号的滤波、压缩、检测和趋势提取都具有较好的应用效果［13］.

1.2 小波分析技术

信号中的有用信息和噪声具有不同的时频特性［14］，有用信息一般为低频且信号相对比较平稳［15］，具有典型的局部化特征；而噪声一般为高频且整个时域内都存在［16］，具有明显的全局性特征. 根据这一特性，小波分析技术可以对信号进行处理［17］，它能够滤除噪声信号、剔除干扰因素的影响，获取信号的趋势.

小波滤波有很多处理办法，工程上常用的是小波阈值法［18］. 小波阈值法可以在信号中提取弱小的、有用的信号，发现并探测出异常值［19］，具有计算速度快、滤波效果好等优势，信号的特征可以被较好地保留下来.小波阈值滤波主要包括以下三个步骤：首先，选取出适合的小波函数，并确定其分解层数，之后对源信号进行处理，可以得到各个尺度对应的分解系数值. 其次，确定了阈值和对应的阈值函数之后，再对分解系数进行相应的处理，得出通过估算的小波系数［20］. 然后，得到小波系数后，分别对其进行处理，最后通过小波逆变换处理，可以得到最终的滤波后的信号.

2 工程实例分析

2.1 项目情况

本文以正在实施地铁变形监测的某区间地铁隧道项目为例进行实验分析. 由于该地铁上行左侧100 m处新建工程需要进行基坑开挖，影响地铁隧道安全，需要对其进行变形监测. 基坑位于隧道北侧，距离隧道最近距离为25 m，最远距离为68 m，基坑与地铁位置关系见下图1.

图1 地铁隧道与基坑相对位置图Fig.1 The relative position of the subway tunnel and the foundation pit

2.2 沉降观测

沉降监测基准点布设在远离变形区外的地铁轨道底板上. 左、右线在变形区外各布设4 个基准点（SJZ1、SJZ2、SJZ3、SJZ4；SY1、SJY2、SJY3、SJY4），共计8个点. 监测点在基坑边线对应区间隧道范围内，左线约每10 m布设一个点（Z3～Z16），右线约每20 m布设一个点（Y3、Y5、Y7、Y9、Y10、Y12、Y14、Y16），边线对应范围外左、右线每隔20 m布设一个点（Z1～Z2，Z17～Z18；Y1～Y2，Y17～Y18）. 沉降监测点布设在轨道底板上，左、右线共布设30个点.

地铁隧道内进行水准测量夜间作业难度大、时间紧、精度要求高. 由于地铁每日要正常营运，因此每天有效的观测时间非常有限，考虑到隧道内观测没有仪器沉降、尺承沉降、光照影响等误差源的影响，水准路线的观测方法拟采用后-后-前-前的观测方法. 水准路线观测的同时进行中视点的测量. 采用Trimble DINI03 电子水准仪进行观测，为了提高测量速度，根据视线长度、视线高度、视距差等控制指标，采取固定仪器站的方法控制这些指标，同时将这些指标预先置入电子水准仪，观测过程中再用随机程序进行控制.

基准网测量或检测采用科傻平差软件进行严密平差，基准网初期进行两次独立观测，误差范围内取均值确定各基准点的初始高程. 历次垂直位移测量起讫于基准点，构成闭合或附合水准路线. 按测站数进行闭合差分配，计算各监测点的高程. 垂直沉降量以上隆为正值，下沉为负值. 左线地铁隧道沉降变化趋势见图2. 说明该地铁隧道整体变化相同，但不同点位存在一定的差异，也无法直接获取观测点的变化趋势和变形周期，这使得事后分析和解读地铁变形情况、变形周期存在困难. 同时，由于沉降量测过程中，受仪器、人为因素或振动等复杂环境的影响，测试结果中的误差往往较高，容易导致变形量测结果失真，从而给分析观测数据和总结变形规律带来一些干扰.

2.3 小波分析

从图2中可以看出，地铁隧道沉降变形量值小，变形量值主要分布在-0.5～+0.5 mm之间，从图中无法获取隧道变形趋势. 为了研究地铁隧道变形中蕴含的变形规律，需要对地铁观测数据进行分析处理. 选择位于变形区中间的Z7、Z8、Z9，Z13、Z14、Z15等6个监测点进行分析，其原始观测值见图3.

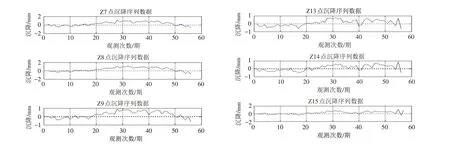
图3 原始观测数据Fig.3 Original observation data

从图中可以发现，Z7、Z8、Z9 三个点位沉降变形量值和振幅较小，变化趋势较为一致. 相比之下，Z13、Z14、Z15三个点变形量值略大，存在振幅较大的点（第56期观测数据），变化趋势有差异. 小波分析时，选择工程中常用的db3小波基，分解尺度选择3层，进行小波阈值滤波，小波变换重构后依次得到Z7、Z8、Z9，Z13、Z14、Z15小波分析后的观测序列，见图4.

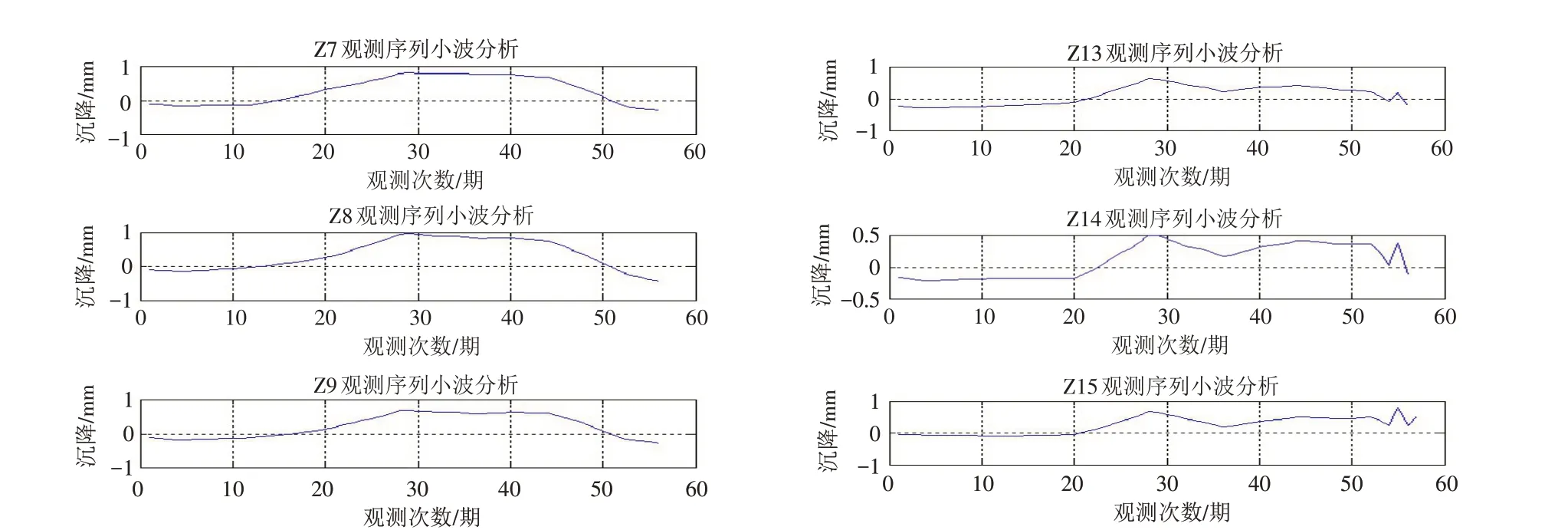
图4 小波分析结果Fig.4 Wavelet analysis results

可以发现，经过小波分析处理后，沉降观测点的变化趋势更为明显. 从上图中看出Z7、Z8、Z9 三个点位的变化趋势相同，均表现为先沉降再上升再下降，前19 期沉降值在0 值附近，第20 期至第51 期表现为上升至最大值然后下降至0 值，第53 期以后表现为逐渐沉降. 结合工程实际情况发现，在前19 期观测时间内地铁左侧的基坑开挖较浅，对地铁隧道的影响不明显，可以认为对地铁无影响. 在第20 期至第51 期时，地铁左侧基坑进行了开挖，随后又进行了混凝土浇筑，因此地铁隧道表现为先上升后又逐步稳定，随后下降，第53 期以后表现为逐渐下降到0 值以下的趋势，说明地铁线路在受到基坑影响上升后又随着建筑物基础的建设逐步下沉. 以上表现均符合工程项目的一般变化规律，验证了小波分析处理地铁沉降数据的有效性.

同时，从上图可以看出，Z13、Z14、Z15三个点位均表现为先沉降再上升，然后逐步下降，趋势与Z7、Z8、Z9三个点位大致相同. 但图中明显可以看出，第56期观测数据出现明显的异常，与上下两期观测数据趋势不符. 经过对比原始数据发现，该期原始观测数据存在误差，导致该期观测数据出现异常，应予以剔除.

以上可以发现，小波分析技术能够滤除信号中的噪声，能够发现信号中的异常值，能够在震荡的原始观测数据中获取变形趋势，为获取地铁变形特性、研究和分析变形规律提供了较好的数据处理手段.

3 结语

地铁安全监测可以获取地铁隧道变形状态和变化趋势，对保障地铁安全和研究地铁变形机理具有重要意义. 衡量地铁隧道安全状态的指标包括：隧道沉降、隧道收敛、隧道水平位移、隧道断面变形等内容，需要对这些监测数据进行准确、实时地处理分析，获取地铁真实变形状态，预测变形趋势，为相关决策提供参考.本文的研究内容证明了小波分析方法的有效性，研究结果为地铁安全监测和相关工程应用提供了参考.