硅单晶辐照中子注量测量的反应截面影响研究
王云波 操节宝 吴清丽 陈 浩 李延鹏 邹 鹏 刘 荣 唐锡定 邓才玉 王万金
(中国核动力研究设计院 成都 610005)
反应堆进行硅单晶中子嬗变掺杂时,为了精确控制产生杂质31P的浓度,通常会采用活化法或自给能中子探测器对中子注量进行测量或监测[1−9],以确保硅体辐照热中子注量准确达到目标值。其中,活化法具有探测器体积小、灵活性高、对中子场干扰小、抗γ射线干扰等优点,是一种普遍使用的测量方法,并且通常会采用一种活化探测器(如Au、Co 和Zr 等)进行测量[1−8]。但探测器目标核素与硅靶核30Si 的俘获反应截面曲线形状存在或大或小的差异,导致活化法测量值与实际值会存在一定偏差,尤其当超热中子对30Si 反应率贡献越大时。其中,Zr目标核素24Zr与30Si的截面形状最为近似,但该探测器热中子反应截面很小,远远小于其他探测器,甚至小于30Si 的截面,且截面和同位素丰度不确定度也较大。目前,仅有韩国的先进高通量中子应用堆在使用[7−8]。因此,为使活化法准确确定与硅单晶目标反应率对应的辐照热中子注量率,需有效抑制反应截面差异引入的测量影响。
本文选用多种活化探测器在岷江实验堆(Minjiang Test Reactor,MJTR)上进行实验,以确定不同反应截面差异的探测器对测量值的影响。为减小测量值偏差,基于Stoughton-Halperin 约定关系和两种活化探测器的组合方式,确立了二元一次方程组求解法,并根据共振积分和0.025 3 eV 热中子反应截面的比值差异,形成了多组探测器组合,比较并分析了通过该方法得到的实验结果。此外,为进一步验证方程组法的可靠性,还形成了基于三种及以上探测器组合方式的线性最小二乘拟合法,并对两种方法的实验结果进行比较。
1 测量方法
1.1 基本原理
当硅单晶或活化探测器在堆内辐照时,不同能量中子对其目标反应率均具有贡献。但快中子反应截面非常小,可忽略不计,只需要考虑热中子和超热中子贡献即可。根据Stoughton-Halperin 约定关系,热中子和超热中子贡献的总反应率可表示为[10]:

式中:R为单核反应率(可通过与活化探测器辐照后活度的关系式确定[11]),s−1;ϕ0为对应于热中子能区的等效0.025 3 eV 热中子注量率,cm−2·s−1;ϕe为超热中子注量率,cm−2·s−1;σ0和I0分别为0.025 3 eV 热中子俘获反应截面和共振积分,cm2;Gth和Gres分别为热中子和超热中子自屏修正因子;g为热能区中子反应截面偏离1/υ规律的修正因子;w′为5kT(k为玻尔兹曼常数,T为中子温度)至镉切割能范围内反应截面偏离1/υ规律的修正因子;f1为该能区超热中子对反应率的贡献因子(室温下数值约为0.468)。
常用热中子活化探测器在较宽能区服从1/υ规律,参数w′可近似为0。Gth和Gres可根据活化探测器尺寸(如片状探测器厚度,丝状探测器直径等)及反应截面等相关参数计算得到[12−13]。将式(1)等号两边除以gσ0,便可得到与热中子和超热中子反应率总和R对应的等效热中子注量率ϕequ:

由式(2)等号右边项可知,当不同活化探测器的I0/gσ0值不同时,其ϕequ值可能有明显差异。尤其当ϕe与ϕ0值越接近时,式(2)右边第二项对ϕequ值的贡献将越大,使得不同探测器的ϕequ值相差越大。由于活化探测器体积较小,将多个探测器布置在堆内相同位置时,可近似认为,其对应的ϕe和ϕ0值分别相同。因此,只要将活化探测器布置在辐照样品适当位置,并确定测量位置的未知参数ϕe和ϕ0,再将其值及样品目标核素的对应参数值代入式(2)右边项后,便可以得到与样品目标反应率对应的ϕequ值。显然,根据式(2)的线性关系,可建立二元一次方程组或者通过线性最小二乘拟合得到ϕe和ϕ0值。
1.2 二元一次方程组求解法
选择两种I0/gσ0参数值相差较大的活化探测器,将其余相关参数代入式(2)后,便可建立求解探测器所在位置ϕe和ϕ0的二元一次方程组:

1.3 线性最小二乘拟合法
选择三种及以上活化探测器,并根据线性最小二乘法原理[14],对式(2)进行变换处理,便可得到ϕe和ϕ0的拟合值:
式中:上标1 和2 表示探测器种类。通过式(3)得到的ϕe与ϕ0值,以及与30Si(或其他辐照对象的目标核素)相关的I0/gσ0值代入式(2)后,便可得到与硅单晶目标反应率对应的ϕequ值。

式中:上标i、j表示探测器种类;n表示种类数目。与二元一次方程组求解法类似,通过式(4)得到的ϕe与ϕ0值,便可确定与硅单晶目标反应率对应的ϕequ值。
2 实验
实验时,将活化探测器布置在如图1 所示的辐照装置内,该装置主要由外靶桶、支撑架和样品架组成。其中,支撑架和样品架均为三层,每层间距100 mm,样品架每层有4 个孔,中心位置1 个孔,外围3个孔,并呈120°夹角。实验前,将种类相同的探测器分别放入1 根密封靶管内,并布置在样品架的T06、T07和T09位置(图1)。

图1 辐照装置及探测器位置示意图Fig.1 Schematic diagram of irradiation equipment and detector location
实验共选择了6 种对热中子敏感的活化探测器,分别为高纯金属Zr 和Fe,以及合金材料CoAl(Co 含量1wt%)、AuAl(Au 含量0.1wt%)、AgAl(Ag含量0.1wt%)和ScAl(Sc含量2wt%),相关参数见表1(反应截面参数来自文献[15−16])。其中,考虑到Zr 目标核素与30Si 的反应截面曲线形状比较近似,二者I0/gσ0值相差较小(表1),因此,将以Zr 测量值作为对比值,以验证本文方法的可行性。辐照装置在MJTR 的5#孔道进行了入堆辐照,辐照期间堆运行功率为5 MW,冷却剂温度约25 ℃。辐照时间约120 min 后,将装置出堆并取出活化探测器,并使用高纯锗γ谱仪收集了放射性活度计数。
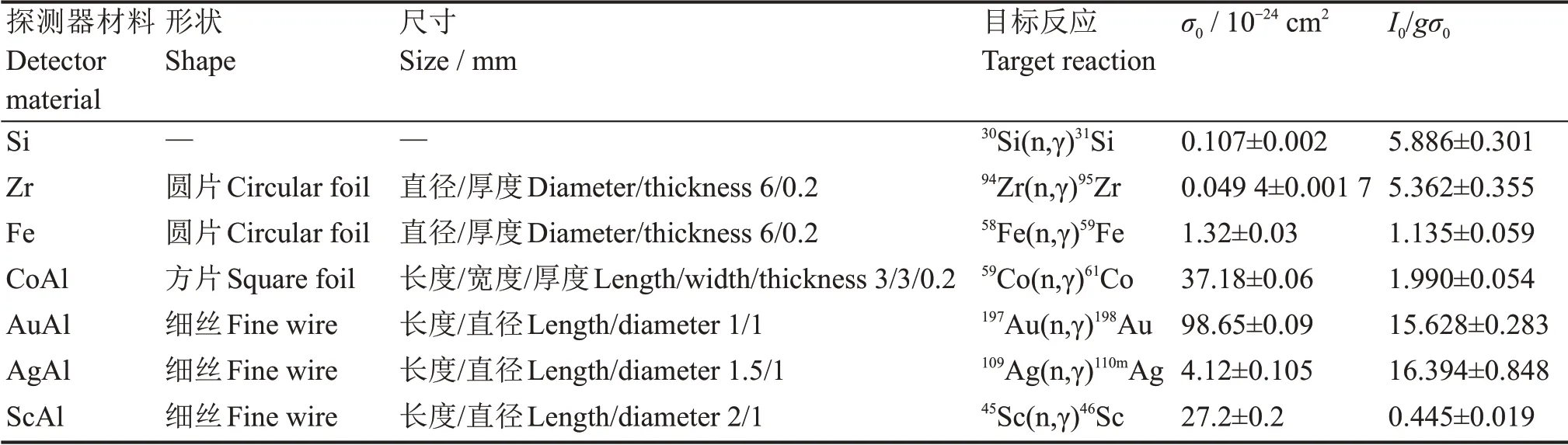
表1 活化探测器相关参数Table 1 Relevant parameters of activation detectors
3 结果及讨论
3.1 不同探测器测量结果
通过高纯锗谱仪收集的活化探测器辐照后的特征γ射线放射性计数、谱仪的探测效率、活化探测器目标核素的总核数及辐照时间、目标产物的衰变常数及γ 射线发射强度等,得到各活化探测器对应的单核反应率R[11],再代入式(2)得到的等效热中子注量率ϕequ测量值(表2)。其中,测量值不确定度主要由活化探测器的质量、目标核素反应截面和丰度、目标产物半衰期和特征γ 射线发射强度及放射性计数、合金材料的目标金属含量,以及谱仪探测效率等不确定度分量合成得到。
由表2 数据可知,同一测量位置的不同探测器ϕequ值具有明显差异,随着I0/gσ0值的增大而逐渐变大。以Zr测量值为对比值,各探测器测量值与其偏差如图2 所示,I0/gσ0值相差越大,对应的偏差越大。尤其AuAl(或AgAl)对应的I0/gσ0值是Zr 的3 倍,对应的偏差已接近25%。对于不同反应堆,或者堆内不同位置,由于其中子能谱不同,式(2)中ϕe与ϕ0相对比值不同,上述探测器测量值偏差也将不同。

图2 不同探测器与Zr测量值偏差Fig.2 Deviation of the measured value between different detectors and Zr

表2 不同探测器的等效热中子注量率测量值Table 2 Measured values of the equivalent thermal neutron fluence rate for different detectors
3.2 二元一次方程组法结果
如表3 所示,以I0/gσ0值相差较大的两种探测器为1 组(不包括Zr 探测器),共分为6 组进行方程组法求解。将各组探测器的ϕequ测量值代入式(3)得到ϕe与ϕ0值,并与Zr对应的I0/gσ0值一起代入式(2)后,确定的与94Zr 反应率对应的ϕequ值如表3 所示,与表2 中Zr 的ϕequ测量值偏差见图3(a),偏差基本小于3%。因此,通过合理的探测器组合,二元一次方程组法能够有效抑制反应截面差异引入的测量影响,大幅减小测量偏差。
为进一步验证方法的适用性,再选择与Zr 的I0/gσ0值有较大差异的Fe 和AuAl 测量值进行比较。利用表3 中探测器组合(不含Fe 或AuAl 的组合)确定的ϕe与ϕ0值,以及Fe(AuAl)对应的I0/gσ0值,得到与58Fe(197Au)反应率对应的ϕequ求解值,与ϕequ测量值的偏差见图3(b)。对于Fe探测器,各探测器组合对应偏差基本在3.5% 以内。对于AuAl 探测器,对应偏差基本在1%以内。因此,综合而言,本方法具有很好的普适性,能够满足不同辐照对象的热中子注量率测量。

图3 方程组法确定值与测量值的偏差 (a) 与Zr测量值比较,(b) 与Fe(AuAl)测量值比较Fig.3 Deviation between the determined value of equations method and the measured value(a) Comparison with Zr measured value, (b) Comparison with Fe(AuAl) measured value
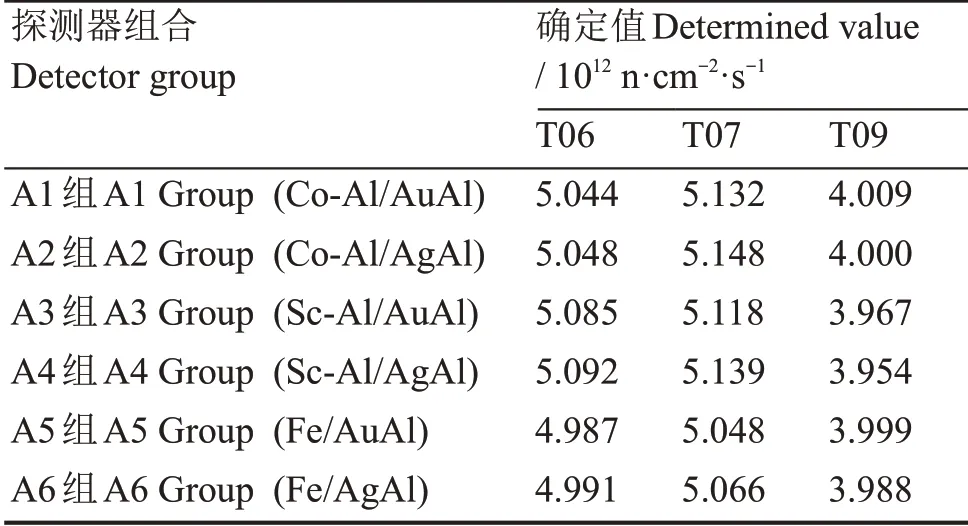
表3 不同探测器组合的方程组法确定值Table 3 The determined value of equations method for different detector groups
3.3 线性最小二乘法结果
如表4 所示,将I0/gσ0值相差较大的探测器分为7组进行了最小二乘法拟合。其中,有6组为3种探测器组合,1组为除Zr以外的5种探测器组合。将通过式(4)得到的ϕe与ϕ0值,以及Zr的I0/gσ0值代入式(2)后,确定的对应ϕequ值如表4所示,与表2中Zr的ϕequ测量值偏差见图4,偏差基本在3% 以内。将B7组与其余组结果比较可知,使用5 种探测器的组合相对3 种没有明显优势,因此,使用最小二乘法时,选用I0/gσ0值相差较大的3 种探测器组合即可。此外,对比图3(a)和图4可知,方程组法与最小二乘法结果相近,进一步证明了方程组法的可靠性。虽然两种方法均能有效抑制反应截面差异引入的测量影响,但方程组法仅需要两种探测器,因此,优先推荐使用方程组法。

表4 不同探测器组合的最小二乘法确定值Table 4 The determined value of least square method for different detector groups

图4 最小二乘法确定值与Zr测量值偏差Fig.4 Deviation between the determined value of least square method and Zr measured value
4 结语
本文通过多种活化探测器测量实验,确定了反应截面差异对活化法测量值具有显著影响。基于Stoughton-Halperin约定关系建立的二元一次方程组求解法,并通过截面差异较大的两种探测器组合方式,能够有效抑制活化探测器与辐照样品目标反应截面差异引入的测量影响,大幅减小测量值偏差,准确得到与辐照样品目标反应率对应的等效热中子注量率。本方法不仅适用于单晶硅辐照热中子注量率的测量,也适用于其他对热中子敏感的样品,并且可选择的探测器种类也较广,不需要考虑活化探测器与样品目标核素的反应截面差异。

