基于双卡尔曼滤波的电池SOC估算

李练兵，孙 坤，季 亮，何桂欣，王 佳，孙腾达

(河北工业大学 人工智能与数据科学学院，天津 300130)

0 引 言

针对储能电池SOC的估算问题，国内外专家学者进行了大量的研究[1-3]。其中，安时积分法、开路电压法和神经网络法等算法为开环估算算法中的代表；卡尔曼滤波法(Kalman filter，KF)、粒子滤波法和滑膜观测器等算法则为典型的闭环估算算法[5]。刘淑杰等提出了基于改进粒子滤波算法、自适应递推最小二乘法与无迹卡尔曼滤波[6-8]的电池SOC估算方法。文献[9]提出了一种使用输入时间延神经网络的锂离子电池SOC估计方法，文献[10]对电池松弛效应及极化现象影响进行建模补偿，文献[11]采用扩展卡尔曼滤波估算电池的SOC，文献[12]提出了基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法，文献[13]提出了一个集成的荷电状态估计模型，文献[14]提出了一种基于减法聚类的神经模糊系统的荷电状态估计方法，都提供了充电状态估计的替代方案，但是实验结果的误差都比较大。针对上述问题，本文采用基于二阶Thevenin模型的等效电路模型，获取状态空间方程，在经过对比电池参数的离线辨识和在线辨识的情况下，采用结合改进协同滤波算法的双卡尔曼滤波(double Kalman filter，DKF)的方法实现电池参数的确定和SOC的估算，经实验验证，采用DKF算法估算电池SOC具有良好的收敛性和精度。

1 锂离子电池参数辨识

1.1 锂离子电池离线参数辨识

混合动力脉冲功率特性(hybrid pulse power characteri-stic，HPPC)测试实验是在电池允许的最大放电倍率下，对电池进行周期性的放电和充电实验，体现动态性能的一种特征[15]。通过记录电池在放电、静置和充电这一运行过程中的电压数据[16]，利用电路的等效电路模型计算出在不同的荷电状态下电池欧姆内阻、电化学极化阻容和浓差极化阻容[17]。

模型参数辨识方法包括离线辨识和在线辨识。离线辨识是通过批量处理实际工况下采集到的数据，结合电路模型的电气特性进行分析计算获得各参数的估计值。在线辨识是根据系统运行过程中的实时数据，通过递推公式不断迭代更新得到模型参数的最优值，二者最大的区别在于实时性。锂离子电池的SOC不能直接测量得到，需要通过开路电压(open circuit voltage，OCV)等外特性来完成对荷电状态的估算。由图1可知，二阶Thevenin等效电路模型中需要辨识参数有开路电压UOCV、欧姆内阻R0、电化学极化电阻R1、电容C1和浓差极化电阻R2、电容C2。结合电路模型的电气特性得到这些参数与实验采集数据函数关系，得到电池等效电路模型参数进而估算电池SOC。本文对电池进行的测试均在恒温箱中进行，设定温度为25 ℃，消除其它的干扰因素同时忽略电池循环寿命对参数的影响。

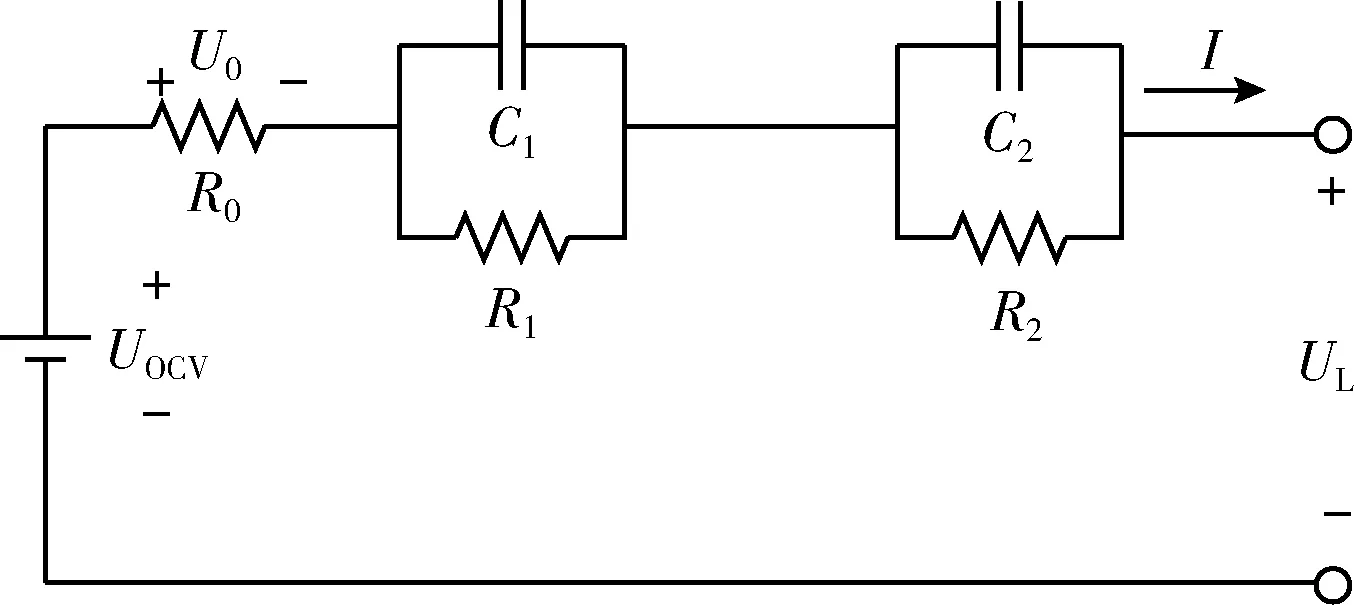
图1 二阶Thevenin等效电路模型

电池处于工作状态下，具体表现为随着荷电状态的减少开路电压随之降低。联合恒流放电和安时积分法计算出电池荷电状态值，同时采集放电过程的电压值，通过提取特定荷电状态值下开路电压数据进行拟合，即可得到OCV与SOC曲线以及函数关系。

对放电过程中的SOC值进行标定，并得出如图2所示的OCV与SOC的关系的拟合曲线，进一步得到OCV-SOC函数表达式。

图2 OCV-SOC拟合结果

相应的函数关系如式(1)所示

UOCV=11.08SOC6-25.581SOC5+17.54SOC4-
1.159SOC3-2.386SOC2+1.263SOC+3.422

(1)

欧姆内阻反映电池端电压的突变特性，表现在电池端电压在放电开始和结束的瞬间产生跳跃式的变化。图3为脉冲放电实验过程中电池端电压的响应曲线。电流加载瞬间，端电压陡降；放电结束瞬间，端电压陡升，这两个压差称为电压回弹特性，利用两个电压差可以求出内阻值。定义图中电流加载前后的电池端电压分别为VA、VB，脉冲电流卸载前后电池端电压分别为VC、VD。

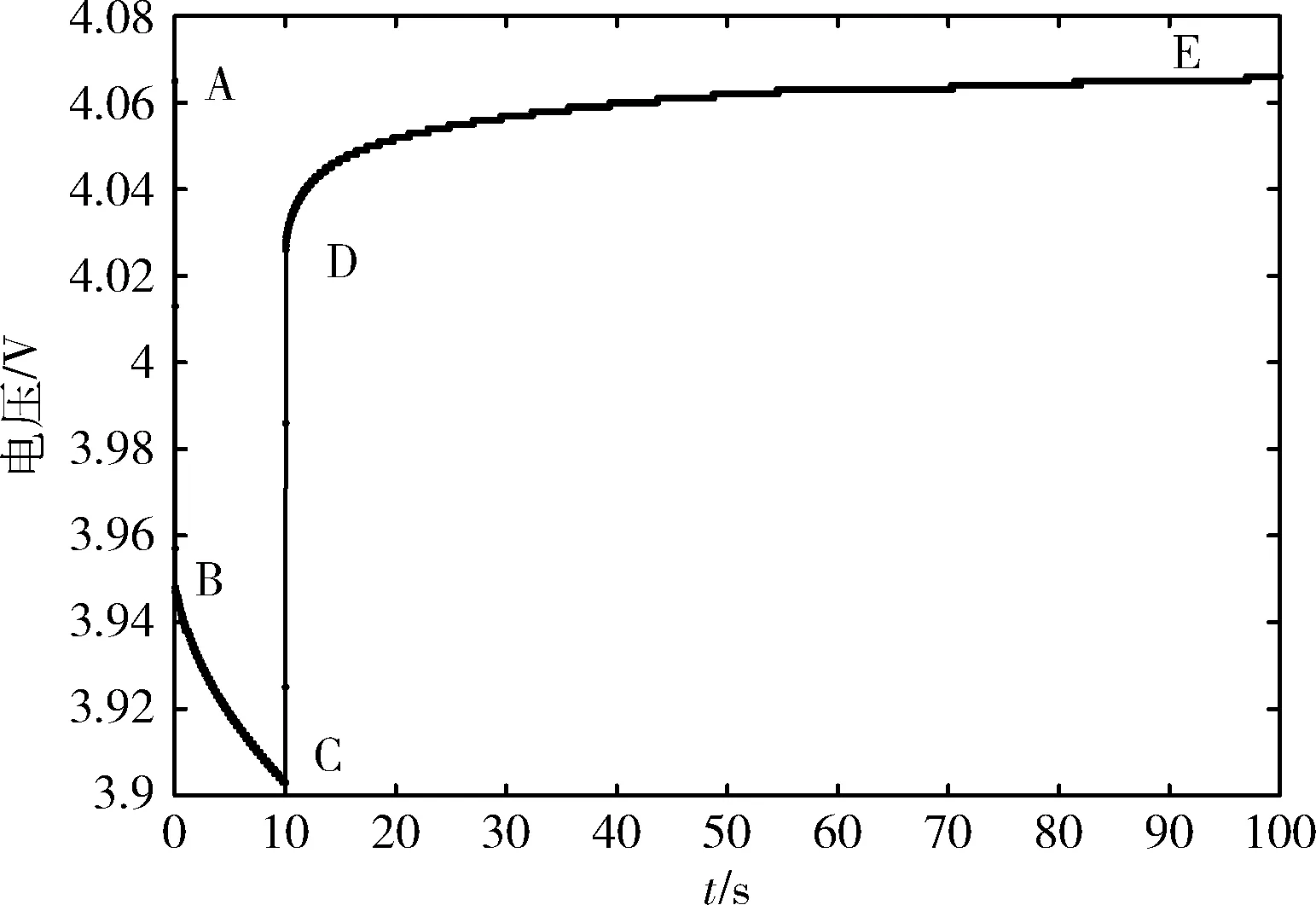
图3 脉冲放电过程中电压响应曲线

为了减少误差带来的干扰，取电流加载瞬间的电压差和电流卸载瞬间的电压差的平均值对脉冲电流的比值作为欧姆内阻，计算公式如式(2)所示

(2)

对不同SOC处求取电池内阻值，得到欧姆内阻R0。

脉冲放电电流卸载后电池处于静置状态下，即图3中从C点到E点的电压变化曲线视为两个RC网络的零输入电压响应，其端电压响应表达式如式(3)所示

UL(t)=UOCV-e-t/R1C1U1(0)-e-t/R2C2U2(0)

(3)

式中：U1(0) 为等效电路模型中电化学极化R1C1网络的初始电压，U2(0) 为等效电路模型中浓差极化R2C2网络的初始电压。

将放电静置阶段电压响应数据导入matlab中，使用cftool中的Custom Equations功能进行指数拟合，根据端电压响应表达式(3)选取的拟合曲线表达式为(4)

y=a-be-ct-de-ft

(4)

式中：a，b，c为常数。

电池静置1 h后，内部的极化反应已经消失，如图3中从A点到C点，此时电压响应为零状态响应，端电压零状态响应表达式如式(5)所示

UL=UOCV-IR0-IR1(1-e-t/R1C1)-IR2(1-e-t/R2C2)

(5)

在C点处，RC并联环节的电压等于初始电压，即

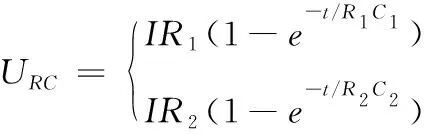
(6)

公式联立，可以求得电池极化参数R1、C1、R2、C2的值。

1.2 锂离子电池在线参数辨识

离线参数表只能涵盖部分工作条件，适用范围具有局限性，因此离线辨识并不能保证跟踪准确性。此外，锂离子电池运行过程中内部化学反应复杂，且受外界环境温度变化影响，通过查表法获取模型的离线参数应用于SOC估算会导致较大的误差。由于电池系统的时变性，为了提高荷电状态的估计精度，提高电路模型的适应能力，需要对参数进行在线辨识并且根据实时采集数据实现参数的更新修正。在线辨识参数基于采集电池工作数据，通过算法更新修正电池参数，追踪电池的实际工作状态[18]。

本文采用结合协同过滤方法的卡尔曼滤波法辨识电池等效电路模型参数。协同过滤算法基于不同的偏好对数据结果进行群组划分并归类相似的数据。电池在线参数辨识步骤分为预测阶段和修正阶段，预测阶段也常称为时间更新阶段，此阶段内容是依据系统的状态方程由k时刻的状态估计值推算k+1时刻的状态先验估计值；修正阶段又称为测量更新阶段，此阶段是通过k+1时刻的实际输出与模型输出的差值对状态先验估计值进行修正，从而使k+1时刻的状态估计值更加接近真实值。模型参数辨识结果及分析如图4所示。

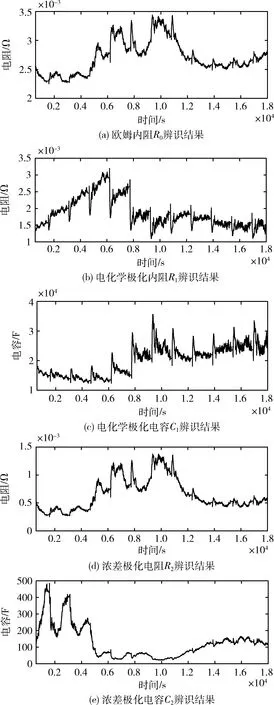
图4 模型参数辨识结果

通过辨识结果可以看出欧姆内阻在整个放电阶段一直保持在3 mΩ左右。两个极化电容差值在两个数量级以上，分别对应在电流突变时电压快速变化的过程以及电压缓慢稳定的变化过程。电化学极化内阻R1和浓差极化电阻R2与相对应的电化学极化电容C1、浓差极化电容C2变化趋势相反。

2 基于二阶Thevenin模型的双卡尔曼滤波估算

2.1 非线性系统的扩展卡尔曼滤波

标准卡尔曼滤波法适用于线性动态系统，当系统非线性时，对系统的非线性方程通过数学中的泰勒公式对方程进行线性化，再进行卡尔曼滤波处理，这个过程称为扩展卡尔曼滤波(extended Kalman filter，EKF)原理。由于电池系统呈现高度的非线性，故采用EKF原理对电池SOC进行估算。

非线性离散系统的状态空间和输出方程如下

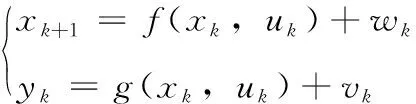
(7)

非线性系统的状态方程框架如图5所示。

图5 非线性离散系统的状态空间模型结构框架

2.2 电池的状态空间模型

本文在二阶Thevenin等效电路模型的基础上，建立了其电池状态空间模型。根据二阶Thevenin等效电路模型，结合安时积分法以电池的SOC、电池极化电容C1两端的电压U1、表征浓差极化电容C2两端的电压U2作为系统的状态变量，充放电电流I(标定放电电流为正)作为输入量，端电压U作为系统的输出量，经过离散化和线性化处理后推导出电池的系统状态方程和输出方程如下所示

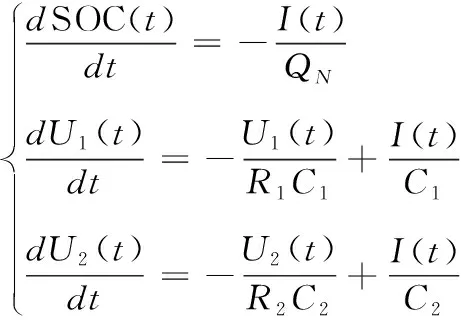
(8)

将上述式子进项离散化后的状态方程为

(9)

式中：Δt为系统采样时间，QN为电池的实际容量， SOC(k) 为k时刻的电池的荷电状态，U1(k) 是k时刻的电化学极化电阻R1两端的电压，U2(k) 是k时刻的电化学极化电阻R2两端的电压，I(k) 为k时刻的电池的工作电流，放电时取正。 SOC(k+1) 通过SOC(k) 加上电流对于采样时间的积分得到。输出方程为

U(k)=UOCV(SOC(k))-U1(k)-U2(k)-RoI(k)

(10)

系统的状态变量为：x=[x1x2x3]T=[SOC(k)

U1(k)U2(k)]T， 系统的输入量为工作电流I(k)， 输出量为电池负载电压UL(k)， 输出方程为UL(k)=I(k)。 通过泰勒公式线性化系统的状态空间模型方程，矩阵参数如下所示

(11)

(12)

(13)

利用线性化后矩阵参数通过卡尔曼滤波算法的递推过程实现对电池SOC的估算。

2.3 电池SOC估算

本文采用了卡尔曼滤波算法对电池二阶Thevenin等效电路模型的参数进行在线辨识，为实际工况下的电池提供实时的模型参数，保证跟踪准确性，有效减小模型误差，使当前时刻电池模型更加准确模拟电池状态，从而提高电池SOC估算精度。基于以上原因，本文结合协同过滤的卡尔曼滤波算法实现电池的在线参数辨识，采用扩展卡尔曼滤波算法估算电池SOC。双卡尔曼滤波估算SOC和模型参数的实施步骤为：

(1)通过HPPC测试实验记录电池在放电、静置和充电这一运行过程中的电压数据，利用电路的等效电路模型计算出在不同的荷电状态下电池欧姆内阻、电化学极化阻容和浓差极化阻容。

(2)采用结合协同滤波的卡尔曼滤波算法进行电池参数的在线辨识并且根据实时采集数据实现参数的更新修正。

(3)将实时参数带入电池空间状态方程，修正电池模型，减少模型误差。

(4)启动扩展卡尔曼滤波对SOC进行估算。

3 基于DKF的SOC估计

为了验证双卡尔曼算法的收敛性和精度，在Matlab中编写了双卡尔曼滤波法估计荷电状态的程序。本文采用UDDS(urban dynamometer driving schedule)测试工况中采集到的电流、电压和荷电状态代入程序来实现对电池的SOC估算验证。分别在参数在线辨识情况下和EKF初值不准确两种情况下对算法进行验证，将实验平台中得到的SOC实际值和EKF程序估算的SOC仿真值以及安时积分法得到的SOC计算值进行分析对比。实验工况过程中电流和电压变化情况如图6所示。

图6 UDDS工况下的电压电流曲线

结合本实验用锂离子电池放电倍率，在国际通用城市道路循环UDDS工况下，缩小一定的比例作为本实验验证的UDDS工况数据，如图6所示。UDDS工况下一个周期放电期间，电流输出的平均值为1.0276 A，最大值为3.884 A，制动过程中产生的最大电流为2.563 A，平均电流为0.2846 A，历时1400 s一个循环，环境温度为25 ℃。

3.1 初值准确

将UDDS实验工况过程的电流和电压变化情况带入双卡尔曼算法程序。算法初始参数为

X(0)=[0 0 0.8]T,P=105e3
Q=10-9，R=0.01

通过图7中的SOC仿真结果可以看到，在UDDS工况下，由于误差积累效应安时积分法计算得到的荷电状态随着电池的放电逐渐偏离实际值，误差积累越来越明显。而双卡尔曼滤波法能很好追踪到实际的SOC值，放电终止时的SOC误差仅为0.3%，仿真过程中最大误差为0.89%，具有良好的精度。图7中仿真结果说明了UDDS工况下，双卡尔曼滤波估算法的效果明显好于安时积分法，能够保证跟踪的准确性。

图7 不同方法SOC估计值

通过图8中的SOC估计局部仿真结果可以看到，在UDDS工况下，随着时间的进行，安时积分法计算得到的荷电状态由于误差积累已经偏离实际值，误差积累越来越明显。而双卡尔曼滤波法前期误差较大，但明显小于安时积分法，并且随着时间的进行，能很好追踪到实际的SOC值，与实际值的误差逐渐减小，具有良好的收敛性。图中仿真结果说明说明了UDDS工况下，双卡尔曼滤波估算法的具有良好的收敛性，能够保证跟踪准确性。

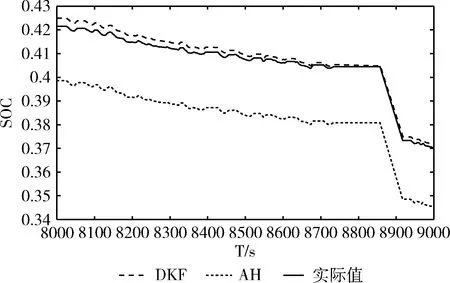
图8 不同方法SOC估计值局部放大

如图9所示，由误差曲线结果可以看出基于二阶Thevenin模型的双卡尔曼滤波算法SOC估计方法的误差曲线变化趋势是一个逐渐收敛至0的过程，而通过安时积分法得到的误差曲线逐渐发散。

图9 不同方法SOC估计结果误差曲线

结果表明，在算法初始值准确的情况下，通过双卡尔曼算法估算的SOC值能够很好的追踪到实际SOC值，其最大误差为0.89%，具有良好的精度和收敛性。

3.2 初值不准确

电池工作在实际工况中，由于异常开关机或者其它故障会导致BMS遗失荷电状态信息，即在不了解剩余电量的初始状态信息的情况下去估算电池系统的SOC值。通过改变双卡尔曼算法的初值，探究算法在初值不准确情况下估算SOC的精度和收敛性。选取剩余电量状态为0.8放电至剩余电量为0.2的数据，将EKF算法初始SOC值设置为0.5。估算结果如图10所示。

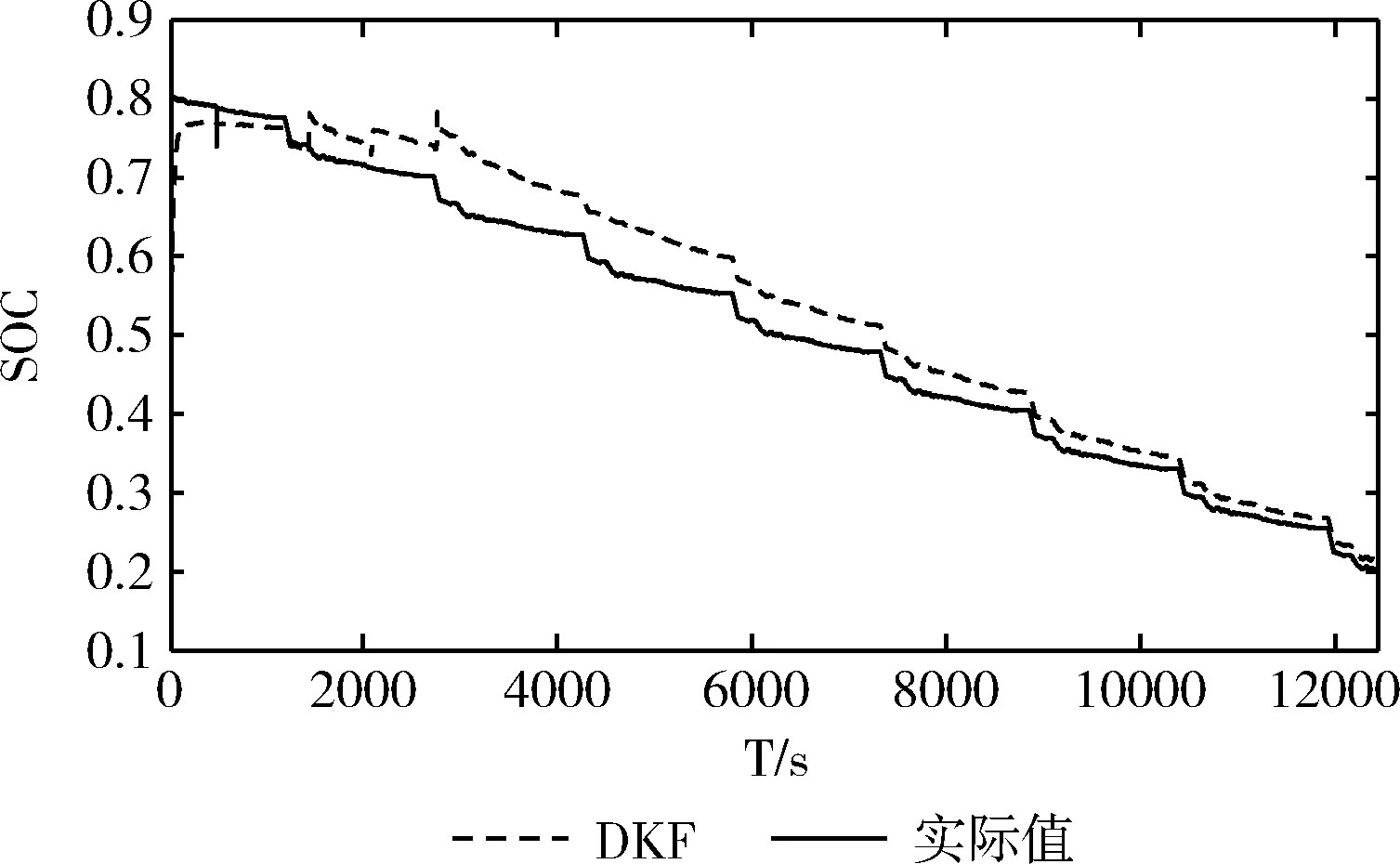
图10 初值不准时SOC估计结果对比实际值

在双卡尔曼算法估计的前期，由于模型初始荷电状态异常，得到仿真值与实际值误差较为明显，尽管这一阶段电池工作在放电状态，算法的SOC估算值却处于上升过程，逐渐追踪SOC实际值。中后期阶段随着算法的递推，估算的SOC值逐渐逼近实际值，误差越来越小。说明通过双卡尔曼算法估算的SOC值能够很好追踪到实际SOC值，具有良好的可行性和收敛性，图11是算法估算SOC值与实际值的误差曲线。

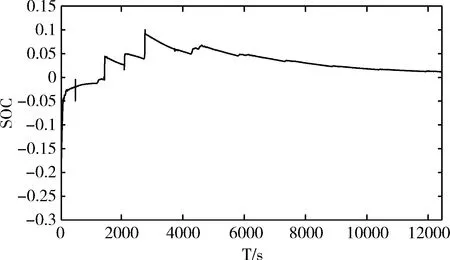
图11 初值不准时SOC估计结果误差曲线

由双卡尔曼SOC误差曲线可以看出误差变化趋势是一个逐渐收敛的过程，在假设算法初值不准确的情况，设定了SOC初值30%的误差，但随着双卡尔曼算法的迭代，误差值逐渐缩小，且始终保持在5%以内。并且在后期，算法估计的SOC值逼近实际值，最终误差小于1.2%。

通过以上仿真结果结果可以看出在剩余电量初始状态准确的情况下，采用双卡尔曼滤波算法估算SOC具有良好的精度和收敛性，估算SOC值逐渐逼近实际值，误差逐渐缩小，最后估算误差保持在1%以内。当初始状态不准确时，随着算法的迭代，采用双卡尔曼滤波算法能通过自身滤波特性，使估算值跟踪实际值的变化，逐渐逼近实际值，且达到稳定状态后误差在5%左右，最终误差保持在1.2%以内。以上验证了双卡尔曼滤波算法估算电池SOC的收敛性、精度以及可行性。

4 结束语

通过对扩展卡尔曼滤波算法的原理进行阐述，在二阶Thevenin电池等效模型的基础上获得离散化的状态空间方程，利用泰勒展开公式将电池的非线性状态方程线性化，结合改进协同滤波的卡尔曼滤波算法在线辨识方法，在Matlab环境下编写了双卡尔曼滤波的SOC估算以及验证程序，基于常温UDDS工况下实验采集到的电压、电流和SOC值，在算法初值准确和算法初值有误差两种情况下对双卡尔曼滤波算法估算SOC的精度和收敛性进行验证。仿真结果表明，在UDDS工况下，采用DKF算法估算电池SOC具有良好的收敛性和精度，具有较高的应用价值。