基于近似最近邻搜索的改进PRM算法

薛 阳，孙 越，叶晓康，李 蕊，华 茜

(上海电力大学 自动化工程学院，上海200090)

0 引 言

机器人的路径规划是机器人领域的基础部分也是核心部分[1]。路径规划的方法也很多，经典的有：人工势场法[2,3]、栅格法[4]、蚁群算法[5，6]等；基于随机采样的路径规划算法有：快速搜索随机树(rapid-exploration random tree，RRT)法[7，8]还有概率路线图(probabilistic roadmap，PRM)法[9]等。相对于需要知道环境中障碍物精确位置并精准建模的路径规划算法，基于随机采样技术的PRM算法可以有效解决高维空间和复杂约束中的路径规划问题。PRM算法广泛应用于移动机器人、机械臂以及无人机航迹规划中。Mohanta JC和Keshari A提出了PRM算法和模糊控制系统结合使用，使得规划的路径更平滑更短，从而缩短了导航时间[10]。邹善习等通过随机节点生成函数在自由空间生成的节点取代障碍物中节点，配合改进的节点增强法，提高节点利用率，减少PRM算法计算量[11]。

PRM算法的改进一般是通过得到更短的最优避障路径，从而减少了移动机器人在行驶过程的时间。PRM算法基于随机采样策略，当增加空间中的采样点或者增加最近邻点个数时，无向路径图的构建将会更完备，最终得到的避障路径会更优。但是以上情况会使得算法运算量呈指数级增长，从而算法非常耗时。针对PRM算法存在的这一缺陷，文中提出引用处理数据的局部敏感哈希算法[12]，加速PRM算法无向路径图的构建，从而提高了PRM算法的效率。在不降低最优路径的质量的前提下，有效提高了PRM算法整体运行速度。

1 传统PRM算法

PRM算法是一种基于图搜索的方法。传统的PRM算法包含两个阶段：离线建图、在线查询。第一阶段离线建图：通过随机采样点将连续空间变成离散空间，然后使用局部规划器将采集的样本节点相互连接并去除与障碍物相交的连线，最终形成了一个无向路径图如图1(a)所示。第二阶段在线查询，使用A*等搜索算法在路径图上寻找无碰撞的最优路径如图1(b)所示。图中方块表示障碍物，浅色细线代表可行路径，深黑色线代表最优路径。

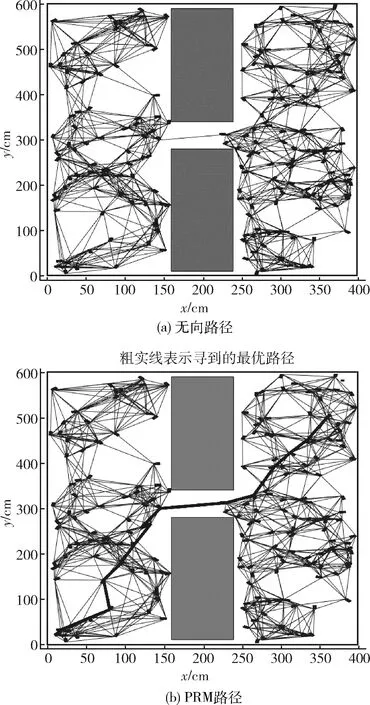
图1 传统PRM算法运行结果

如算法1显示的一个典型的PRM算法。从一个空的路径图G=(V，E)开始，其中V是给定的自由空间Cfree中生成的随机点集，E是所有可能的两点之间的路径。

(1)在自由空间中生成随机采样点q，从而确保机器人在采样点不会与障碍物相碰撞。生成这些采样点的最简单方法是使用均匀分布随机采样。另一个简单的方法是使用低差异序列来产生样本。在一些完全随机的环境中，上面两种方法已经足够。但是移动机器人所处的环境一般更组织化和结构化。例如，移动机器人在房屋里移动，则墙壁和家具都会成为障碍物，并且在较大的空白区域机器人都可以自由移动。这类环境中，要使用不同的方法来增强采样，一些方法尝试在障碍物附近节点采样，而其它方法尝试对障碍物尽可能远的节点采样。还有一些方法可以将配置空间划分为不同的区域，然后尝试检测对每个区域进行采样的最佳方法。

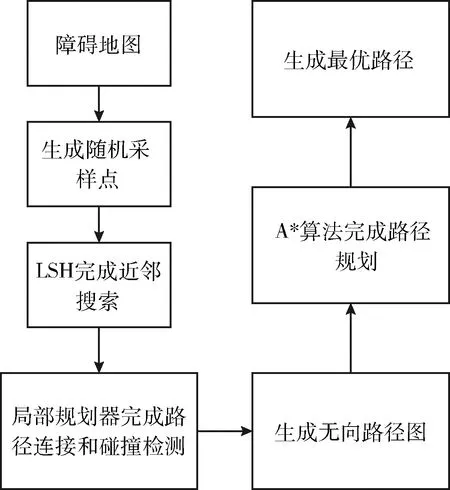
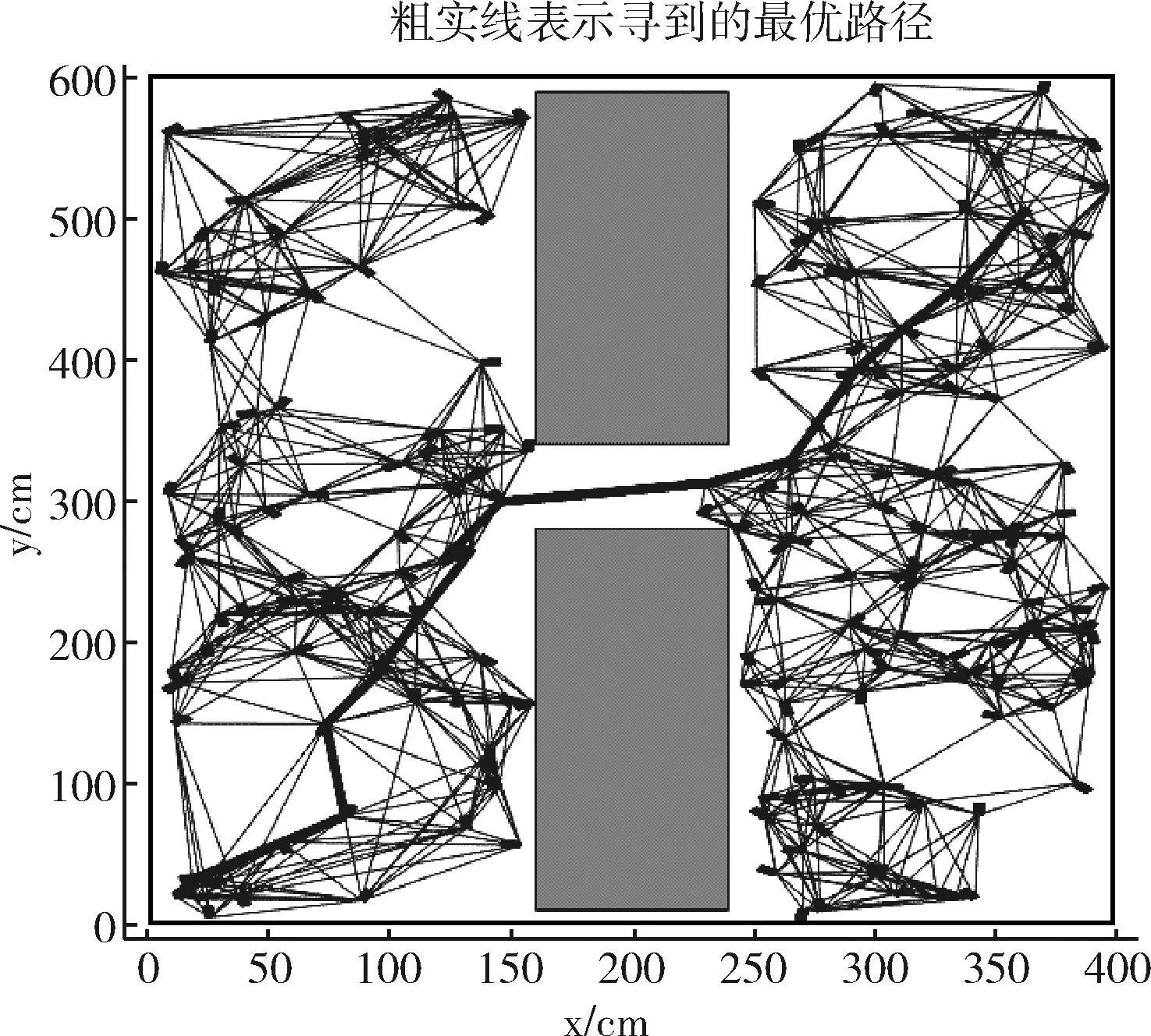
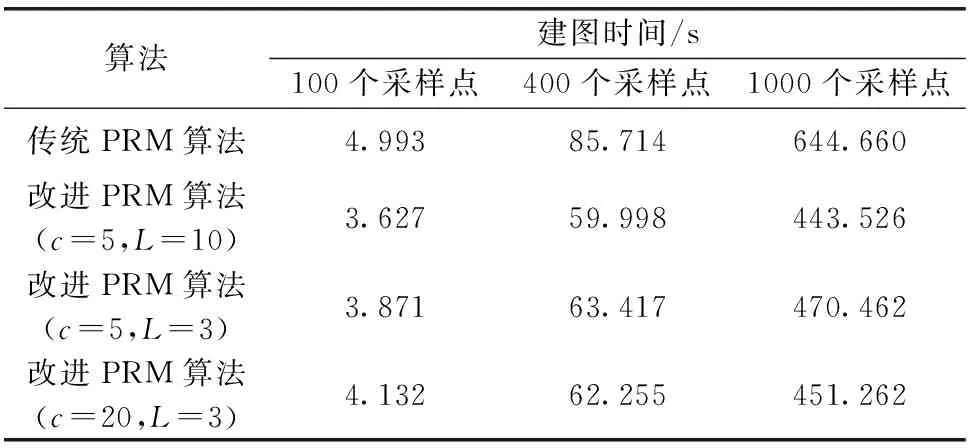
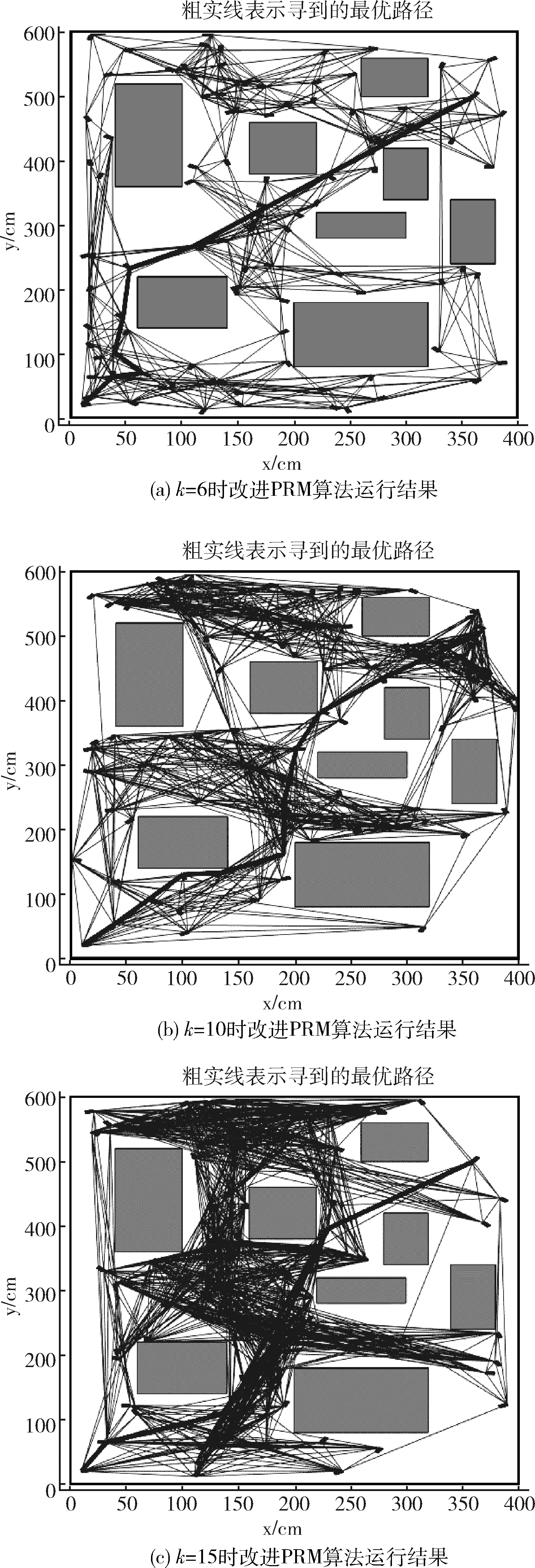
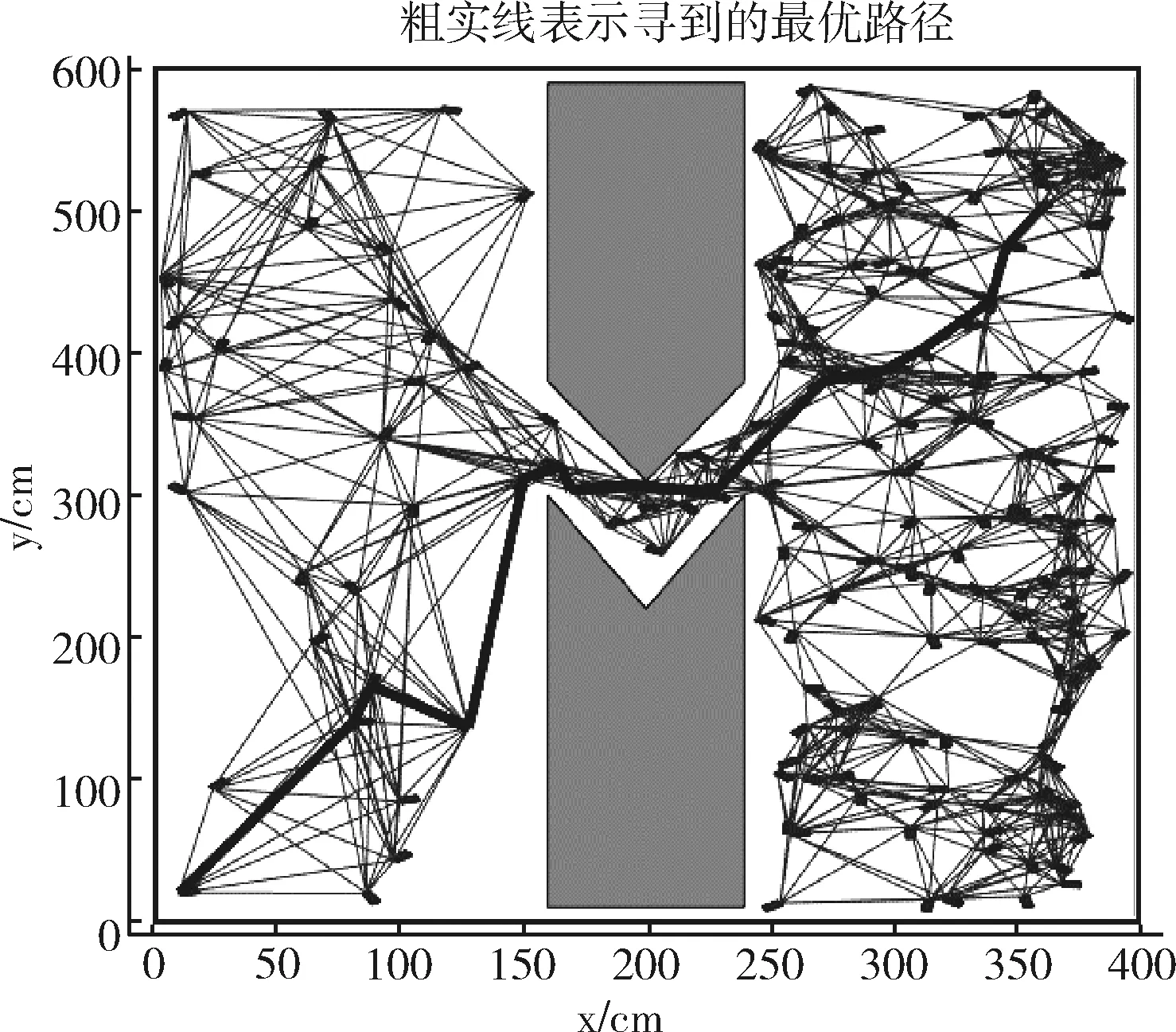
(2)根据一个度量选取k个q点的近邻点，近邻点选取的度量指与q点的距离在一定的范围即N0={n∈N│L(q,q′)

(1)

式中：ωMi∈R，是权重常数。

(3)使用局部规划器检测q点和k个近邻点是否存在路径，如果有，相互连接形成机器人的移动路径，并且经过碰撞检测后删减掉与障碍物相交的路径。

(4)生成的路径加入到集合E中。最终所有随机采样点相连成一个无向路径图。

算法1：传统PRM伪代码

Constructs the roadmapG=(V,E)

V←∅

E←∅

repeat

q←sampled configuration fromCfree

V=V∪{q}

Nq←knearest neighbor configurations ofqchosen fromV

for allq′inNqdo

ifqandq′are not in the same

component of the roadmap then

if local planner finds a path

betweenqandq′then

E←E{(q,q′)}

until there are enough configurations inV

returnG

从算法1可以看出PRM算法在每次向路径图中添加新节点时必定要找到一组最近的相邻节点。然后通过局部规划器寻找新节点到每个近邻点的自由路径。因此使用PRM算法时，大部分工作是在无向路径图的构建。

局部规划所做的碰撞检查是构建无向路径图时最耗时的部分，也是PRM算法最耗时的部分之一。因此，不可能检查所有路径是否发生碰撞，而是选择一组相邻节点调用一次局部规划。

最近邻搜索是PRM算法的重要组成部分，因为对于每个采样点，都需要搜索一组最近邻节点。当路线图规模增加时，这会成为一个非常耗时的操作。所以邻域搜索和碰撞检测是PRM规划的瓶颈之一。当工作空间环境复杂，尤其是高维空间中，更是成为性能的主要瓶颈。

2 搜索算法优化

PRM是概率完备且不最优算法，但在PRM中通常使用精确的最近邻搜索。这非常耗时，尤其处理复杂环境下大量数据时更加耗时。近似最近邻查找(approximate nearest neighbor,ANN)可以很好加速查找过程，提高算法效率。而局部敏感哈希(locality-sensitive hashing,LSH)便是属于近似最近邻查找的一种。通过使用局部敏感哈希搜索算法来加速PRM算法中无向路径图的建立，从而提高PRM算法运行速度。改进PRM算法流程如图2所示。

图2 PRM算法流程

2.1 局部敏感哈希

LSH的基本思想：基于原始数据空间中相邻的数据经过同一个映射变换之后，处于相邻区域的概率仍然较大，选取一些具有上述性质的函数来作为哈希函数，使得相邻的数据映射后处在哈希表的同一个位置，更容易搜索与目标数据相似的数据集。当哈希函数h满足以下的两个条件，称h为局部敏感哈希函数：

(1)如果L(q1,q2)

(2)如果L(q1,q2)>d2，则P[h(q1)=h(q2)]≤p2；

其中，d1，d2，p1，p2是给定的常数，L(q1,q2)表示q1，q2两点之间的相似程度，P[h(q1)=h(q2)]表示q1，q2两映射的哈希值相同的概率。

通过选取的哈希函数h映射变换能够将原始数据集划分为若干较小的子集，每个子集中元素个数较小且相邻。因而把超大集合内查找相邻元素变成了在一个小集合内查找相邻元素，计算量因此大大下降。该方法不能保证精确找到与某个数据最相似(距离最近)的一个数据或多个数据，但是会以很高的概率返回非常好的近似值。

LSH方法基于包含多个存储桶的哈希表。每个存储桶都和唯一的哈希值关联，并且使用哈希函数h计算移动机器人工作空间M中点的哈希值。通过函数h的映射，将M中所有点存储到存储桶中，一个存储桶中包含多个点。当搜索邻近查询点q∈M的一组点，首先计算q的哈希值。从得到哈希值指示的存储桶中检索所有点。哈希表可以实现为非常有效地工作，这意味着在实践中可以快速完成这些点的搜索。但是，不确定所找到点是否包含q的最近邻居。通过使用多个哈希表，可以增加该方法找到最近点的概率。创建包含多个哈希表的L表，并且为每个哈希表使用一个不同哈希函数。算法2展示了如何将新点添加到每个表中。

算法2：哈希表中添加点伪代码

(1)fori=1,2,…,Ldo

(2)h←hash value forqinith hash table

(3)b←bucket identified by a valueh

fromith hash table

(4)Add pointqto the bucketb

使用LSH检索邻近点时，首先从每个表中获取点，然后将它们组合在一起，如算法3所示。

算法3：伪代码

Returns k nearest nodes to a query pointq

(1)V←∅

(2)fori=1,2,…,Ldo

(3)h←hash value forqinith hash table

(4)b←bucket identified by a value h fromith hash table

(5)V′←all nodes from bucketb

(6)V←V∪V′

(7)returnV

LSH算法中，哈希函数的选择尤其重要，哈希函数选择条件：如果两个数据点彼此相邻，则经过哈希映射变换后这两个数据点很有可能返回相同值。这意味着哈希函数将保留位置信息，并且彼此邻近的点可能会存储在哈希表同一存储桶中。常见满足不同距离度量方式的局部敏感哈希函数有：基于欧氏距离哈希函数、基于余弦距离哈希函数、基于Jaccard距离哈希函数、基于汉明距离哈希函数、基于质心哈希函数等等。而基于质心哈希算法[13]易于实现，并且可以扩展以满足PRM算法的需求。

2.2 基于质心的哈希函数

在基于质心的哈希函数中，开始时会生成一组质心c。质心属于移动机器人工作空间M，通过计算从q到每个质心的距离，然后选择最接近的质心，任意点q∈M可以与其中一个质心相关联。这实际上将空间M划分为c个分区。这种划分也可以被认为是Voronoi图，其中每个质心对应一个Voronoi单元。因此哈希函数h可以定义：取得一个点，计算它属于哪个Voronoi单元，返回与该单元关联的哈希值。使用此哈希函数，存储桶数量将与质心数量相同。

在图3中以二维方式说明了基于质心的哈希。在图3(a)～图3(c)中，出示了3组不同的质心和相应Voronoi单元。质心用小点标记，中间以小圆表示查询点q，q所属单元格用灰色标记。要为q检索一组最邻近的点，从这3个有标记的Voronoi单元检索即可。

图3 基于质心的哈希

基于质心的敏感哈希算法要在PRM算法中应用进行改进PRM算法，需要解决两个问题：如何选择质心；如何处理路线图中只有几个节点的情况。

第一个问题是选择质心。最简单的方法是生成c个随机点用作质心。这是可行的，但会忽略从环境中得到的一些信息。在此基础上提出了一种考虑静态障碍物的方法。初始化质心的方法如算法4所示。假设路线图一开始是空的，这意味着不可能使用关于现有路线图信息。因此，该方法随机选择质心，但要求所有质心都位于自由组态空间Cfree。为了在空间中更均匀地分布质心，可以使用一些低差分序列来生成质心。在改进PRM方法中应该注意，如果c大于1，那么L也必须大于1。否则，路线图将在每个Voronoi单元中单独构建，不会连接在一起。通过增加L，单元之间会有重叠，有助于路线图连接起来。

算法4：用质心c初始化L哈希表伪代码

(1)fori=1,2,…,Ldo

(2)P←∅

(3)fori=1,2,…,cdo

(4)P←a random free configuration

(5)P=P∪{q}

(6)Associate centroidsPwithith hash table

第二个问题是路线图只有几个节点的情况。例如，为一个查询点q检索k个最近邻，而路线图只有k个节点，那么应该返回路线图中所有节点。但是，算法3中所示方法可能只返回所有节点的一小部分，因为它只返回某些存储桶中节点。算法5给出了一种改进方法。如果路线图的节点数少于k个，将立即返回所有节点，否则将确保始终返回k个最近的节点。

算法5：伪代码

(1)if|R|≤kthen

(2)returnR

(3)V←∅

(4)fori=1,2,…,Ldo

(5)h←hash value forqinithhash table

(6)b←bucket identified by a valuehfromith hash table

(7)V′←all nodes from bucketb

(8)V←V∪V′

(9)if|V|≤kthen

(10)returnknearest nodes toqfromR

(11)else

(12)returnknearest nodes toqfromV

3 仿真结果与分析

3.1 一般环境下仿真

为了验证改进后PRM算法效果，使用matlab2017b仿真软件对改进PRM算法进行仿真实验，仿真实验中设置了400×600大小的地图，单位设置为厘米(cm)，场景中方块表示障碍物，浅色细线代表可行路径，深黑色线代表最优路径。设置机器人起始点坐标为[10,20]，目标点为[360,500]，在地图中选择随机点数分别为100、400、1000,此时最近邻数目k设置为6，生成的无向路径图和如图4(a)～图4(c)所示。图4中显示出，随着随机点数增加无向路径图构建更为详细。

图4 改进PRM算法生成的无向路径

无向路径图构建完成后，使用搜索算法进行最优路径查询，生成一条由起始点至目标点的最优路径。图5显示的是使用改进PRM算法得出的移动机器人避障的最优路径，图中粗实线表示搜索出的机器人移动的最优路径。对比图1(b)和图5，改进PRM算法得出的最优路径基本与传统PRM算法得出的路径相同，这是因为加入LSH搜索算法的改进PRM算法仅加速了构建无向路径图的速度，所以得到最优路径的质量并没有下降。

图5 改进PRM算法生成的避障路径

在仿真实验中，为了减少因PRM算法随机性而产生的误差，对传统PRM算法和改进PRM算法分别进行了40次实验取平均值，采样点的近邻点个数k设置为6，随机采样点数分别设置为100、400、1000。为了找到合适的参数c和参数L的值，在改进PRM算法中给c和L设定不同的值。实验结果见表1。

表1 一般环境下改进算法与传统算法实验数据对比

由表1的数据可以得出：相对于传统PRM算法改进后PRM算法在建立无向路径图的时间上减少了27.36%～33.27%，且随着随机采样点的数目增多，改进后的PRM算法效率逐渐增加。当采样点数目相对不多时质心数目越多，反而算法运行时间增大。随着采样点增多，质心数目相对增加时更有利于减少算法时间。哈希表数目相对增多有利于算法提高效率。

3.2 多障碍物环境下仿真

同一般环境相同的仿真环境下，在地图中添加8个障碍物。实验步骤和一般条件下实验步骤相同，随机采样点数设置为100，c设置为5，L设置为3。当近邻点数目k设置为6、10、15时，对应的结果如图6(a)～图6(c)所示。通过对比可以得知，随着k值增大无向路径图变得更加完备，而规划的路径也更优。

图6 改进PRM算法运行结果

实验结果显示，在多障碍物的复杂地图环境下，改进PRM算法相比较传统PRM算法，在建立无向路径图时间上减少了28.61%。随着k值的增大构建无向路径图的时间也有所增加。实验数据见表2。

表2 多障碍物环境下改进算法与传统算法实验数据对比

3.3 狭窄环境下仿真

仿真环境不变，在地图中添加障碍物构建一个狭窄环境，设置机器人起始点坐标为[10,20]，目标点为[360,500]。随机采样点数设置为200，c设置为5，L设置为3，近邻点数目k设置为6。实验的步骤和一般条件下的实验步骤相同。使用改进PRM算法最终生成的最优路径如图7所示。

图7 改进PRM算法运行结果

因为PRM算法的随机性，进行50次仿真实验。实验结果表明，在狭窄环境下，改进PRM算法时间减少了27.57%～27.71%。50次狭窄环境下的仿真中，传统PRM算法出现了23次最优路径无解的状况，改进PRM算法也出现了23次最优路径无解的结果。因为在狭窄环境下，随机点洒在狭窄通道的几率会减小，从而构建出的无向路径图会有缺失，在在线搜索环节就会搜寻不到从起始点至目标点的最优路径。

4 结束语

本文基于传统的PRM算法，使用基于质心的局部敏感哈希算法加速无向路径图的构建，从而减少了PRM算法的运行时间，提高了PRM算法的运行效率，且搜索的最优路径质量并没有下降。并通过移动机器人在一般环境地图和多障碍物环境地图以及狭窄环境地图的仿真实验，验证了改进PRM算法确实节省了算法在建立无向路径图环节的时间，提高了算法运行速度。