考虑直流偏磁的变压器状态分析及量化评价

李 晖，钟卓江

(四川能投发展股份有限公司，四川 成都 611130)

0 引 言

随着中国交直流电网的逐步发展，交直流网架结构正在逐渐成形。在混联系统中，当直流输电系统在单极大地回路运行、调试时，该方式将会向大地流入几千安培的电流，使周围处于中性点接地状态的变压器发生直流偏磁现象，并造成噪声、振动、损耗增大等有损变压器运行的现象。

若要考虑直流偏磁对变压器状态的影响，需要正确的方法对其评价，该评价方法不仅是确保变压器安全运行的基础，更是变电站运行维护人员合理安排检修计划的重要参考。由长期的现场运行情况可知，经常性的直流偏磁将会使变压器的各部分受到影响，进而日积月累产生不良的运行状态，甚至损坏设备。如文献[1-4]分析了直流偏磁对变压器噪声、振动、损耗的影响，使变压器噪声、损耗增大并且产生振动现象。文献[5]研究了直流偏磁对变压器连接组别的影响，分析了不同的连接组别受直流偏磁的不同影响。但上述文献研究的侧重点在直流偏磁对变压器产生的具体影响上，未从整体定量考虑如何影响变压器的整体运行状态。

目前变压器状态评价的方法有多种，如神经网络、贝叶斯网络、模糊理论等，都取得了较好的评价效果，但是考虑直流偏磁影响的工作鲜有报道。文献[6]虽然考虑了直流偏磁对变压器状态评估的影响，但其评价方法采用人工经验法，评价结果易受主观影响。

基于此，提出了考虑直流偏磁影响的变压器状态分析及量化评价方法。首先，从直流偏磁产生的现象出发，定量分析了直流偏磁对变压器状态的影响；其次，给出了考虑直流偏磁影响的具体表达式，在此基础上，建立了考虑直流偏磁影响的变压器状态量化评价模型并优化了模型的客观性，使之更能反映变压器的状态；最后，通过实际案例的对比分析，证明了该方法的有效性，量化了直流偏磁对变压器状态的影响程度。

1 直流偏磁产生原理

当直流输电系统在单极大地回路运行、调试时将产生电位差，直流侵入变压器中性点，产生直流偏磁现象。

当直流偏磁发生时，其磁通变化情况如图1所示；变压器交流部分iac和直流量idc叠加为励磁电流的大小，如式(1)所示。

i=iac+idc

(1)

Hl=Ni

(2)

式中：H为磁场强度；l为主磁路长度；N为线圈匝数。

将式(1)、式(2)和方程B=μH代入磁通表达式Φ=BS，可得

(3)

式中：μ为磁导率；S为截面面积。

因此，当变压器中性点电流出现交直流叠加情况时，将出现直流偏磁。与原始磁通相比，叠加后的总磁通多了直流磁通分量，这将使磁化曲线到达非线性区域导致铁芯饱和，产生畸变的励磁电流，进而导致变压器内部振动现象加剧，如图1所示。同时，由实际运行经验判断，当直流偏磁发生时，变压器内部振动、噪声和损耗等单个因素的变化相对不大，因此，通过多维因素叠加评判分析直流偏磁对变压器状态的影响。

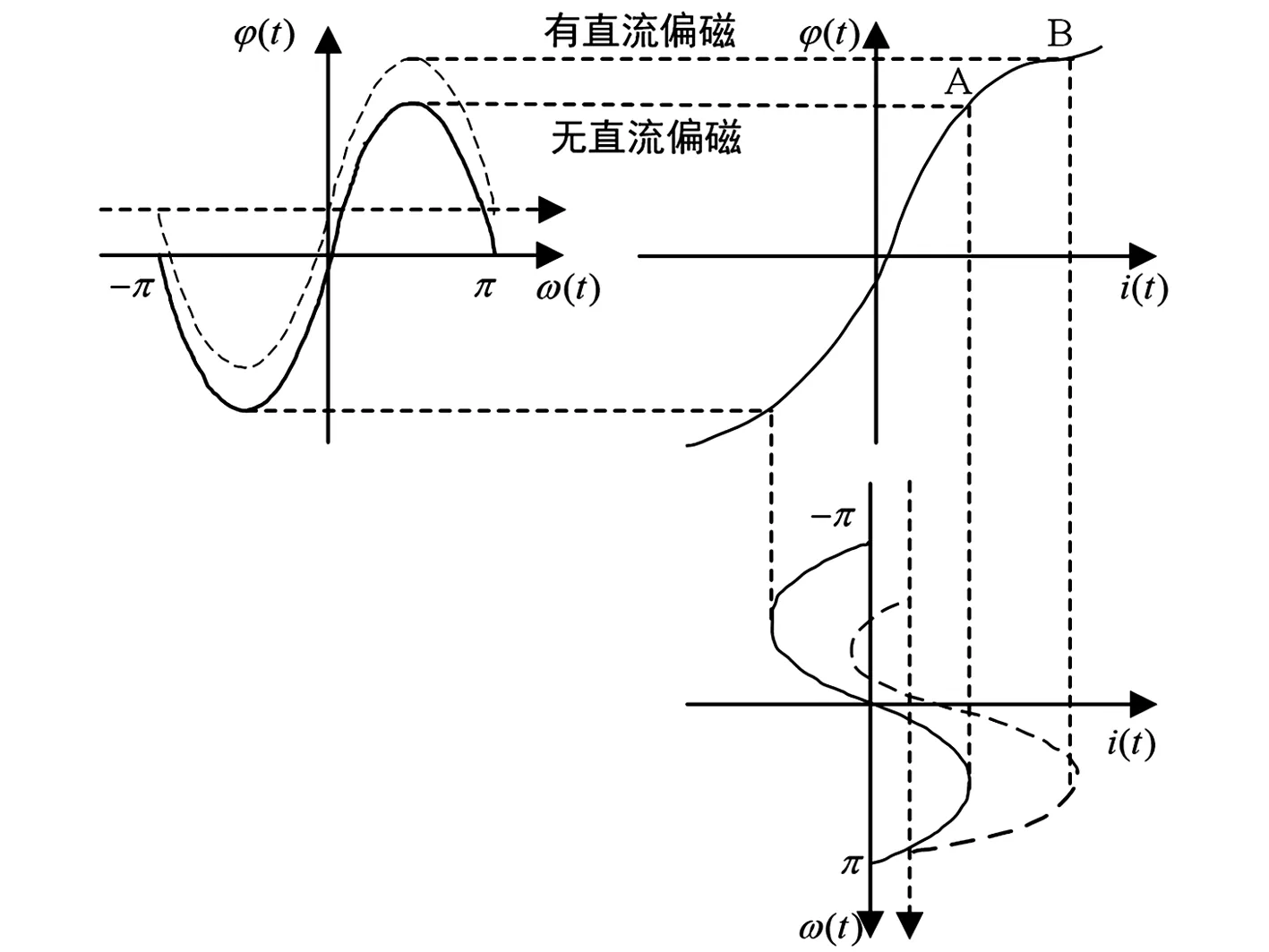
图1 直流偏磁产生原理

2 直流偏磁对变压器运行的影响量化

2.1 对变压器噪声的影响

当变压器发生直流偏磁时，不仅会加剧变压器的振动频率，也会导致噪声的增大。通过分析文献[7]的噪声C与中性点直流idc的数据，得到了两者的近似关系式如式(4)所示。

C=mlg(idc+8)+n

(4)

式中，m和n为常系数，具体确定方法见第3.1节。由于变压器产生的噪声对其周围居民的生产生活有直接的影响，因此，在量化评价变压器状态时，需要考虑居民生产生活可以接受的噪声水平，这也利于贯彻国家提倡的环保策略。由此，通过查找有关噪声水平的规定，确定居民区的最小噪声标准为45 dB。同时，考虑到变电站和居民区之间的距离将会产生部分传播损耗，通过国际通用衰减公式可以计算噪声衰减量，如式(5)所示。

(5)

式中：ΔC为噪声衰减量；d、h分别为变压器油箱的宽度和高度；L为测量点到箱壁之间的距离。

联立式(4)和式(5)可得到不影响居民生产生活的变压器中性点直流限值。

在找到噪声与变压器中性点直流之间的关系后，进而对变压器的噪声进行量化评价。下面通过指数函数进行量化评价，同时为了方便计算，将量化数据进行同向化处理，即量化结果均在[0,1]区间内，并且数值越小，影响越小，运行状态越好。直流偏磁对变压器噪声影响的量化表达式如式(6)所示。

(6)

式中：fl(idc,tn)为考虑直流偏磁后的噪声评估值，取值范围为[0，1]；idc为中性点直流电流；tn为噪声持续时间；im和is分别为不同噪声值下的函数分界值，由式(4)和式(5)计算所得。

2.2 对变压器振动强度的影响

由上节分析可知，铁芯磁通饱和是使变压器振动加剧的原因。根据文献[4]得到振动位移与磁通的近似正比关系，同时考虑到振动加速度和振动的剧烈程度对振动的影响，可得到式(7)。

(7)

时间窗口的确定由中性点直流的设定而定。当中性点直流超过设定的限值时，时间窗口开始计时并开始计算能量系数，直到小于中性点直流设定值结束并停止计算能量系数。

由上述分析可知，振动强度对变压器状态的影响成正相关，因此，采用升半梯模型进行量化分析，直流偏磁对振动强度影响的量化表达式如式(8)所示。

(8)

式中：f2(Ec)为考虑直流偏磁后的振动强度评估值，取值范围为[0，1]；Ece1和Ece2是由式(7)求得的阈值；m2为常系数，具体确定方法见第3.1节。

2.3 对变压器损耗的影响

当直流偏磁发生时，若变压器长期在此状态下，其产生的偏磁电流将会使变压器的空载和负载损耗增加。当计及直流偏磁的影响时，通过两部分进行损耗计算。一是空载损耗的计算，在2.5个周期内分别通过计算得到的励磁电流有效值查找相应的变压器空载损耗P1和P2，由此可得到考虑直流偏磁的空载损耗表达式；二是负载损耗的计算，根据常规负载损耗计算方法进行。由此可以得到考虑直流偏磁影响的变压器损耗计算公式如式(9)所示。

(9)

式中：Pa为空载损耗；Pl为负载损耗；P为总损耗；P0为冷却器容量；IN为负载电流；Idc为发生直流偏磁时变压器中性点的直流电流；ΔT为变压器油温的温升；c、M和R分别为变压器油比热容、质量以及变压器损耗等效电阻。

由上述分析可知，变压器损耗对其状态的影响成正相关，因此，同理采用升半梯模型对其量化分析，直流偏磁对变压器损耗影响的量化表达式如式(10)所示。

(10)

式中：f3(P)为取值在0～1之间的变压器损耗评估值；Pe1和Pe2为计及直流偏磁对变压器损耗影响的阈值，由式(9)求得；m3为常系数，具体确定方法见第3.1节。

3 直流偏磁对变压器状态影响的量化评价

3.1 系数确定方法

在考虑噪声、振动强度和损耗对变压器的影响量化中，产生了一些待定系数以及影响权重集参数。文献[8-11]在处理待定系数时，采用人工统计打分方法确定，具有很强的主观性，而通过使用统计分析软件SPSS进行大数据拟合分析，确定这些待定系数，更具客观性和可行性，如图2所示为待定系数确定流程。

图2 待定系数确定流程

确定系数时，把出现直流偏磁下的变压器基础运行数据分为拟合数据集和验证数据集。首先，对基础运行数据进行数据清洗，去除异常数据点；然后，输入拟合数据集进行数据拟合；接着通过验证数据集对系数进行验证，若验证成功，则确定系数，若验证失败，返回到数据清洗步骤，更新数据库，再次拟合，直至输出系数。

通过上述系数确定方法，采用实际运行的某220 kV变电站变压器的运行数据进行拟合分析，得到待定系数和权重系数。

由上可知，系数确定及量化评价所需的数据有变压器基础数据和运行数据两部分。基础数据有变压器的尺寸数据，运行数据包括由振动传感器监测的变压器本体加速度、采样时间间隔和采样数量、变压器油温数据以及变压器励磁电流、中性点直流电流等运行数据。同时由于变压器结构的不同将会导致直流偏磁对变压器状态的影响不同，因此，选取了输电网常用的三相变压器和单相自耦变压器数据分别进行系数确定。

根据待定系数确定方法可求得不同的变压器结构类型相关系数值如表1、表2所示，其中待定系数通过发生直流偏磁时的数据拟合而得，权重系数通过正常运行数据和发生直流偏磁时的数据共同作用下拟合而得。

表1 三相式结构相关系数值

表2 单相自耦式结构相关系数值

3.2 模糊综合评价

模糊综合评价的基础是模糊集合论，该理论主要作用是提供受模糊因素影响或对多类型模糊因素现象分析的评价方法。模糊关系可以定量分析主观性强和边界不清的因素，并对多类型因素进行综合性评价。该评价方法结果清晰，极具客观性，是一个好的问题解决思路。

在前述直流偏磁对变压器运行影响量化的基础上，首先求出噪声、振动、损耗量化表达式的相关系数；然后将量化表达式融入模糊综合评价中；最后通过模糊综合评价方法对变压器状态进行评价。

采用加权归一化后的评分方式对变压器受直流偏磁影响的状态进行评价，状态划分参照文献[12-14]进行，划分结果如表3所示。

表3 变压器状态划分

变压器状态模糊综合评价有如下步骤：

3)建立评估集V。变压器状态评估集由正常状态、注意状态、异常状态、严重状态等4类状态构成。

4)建立隶属度矩阵。其表示从状态变量集F到评估集V的模糊关系，并从中得到单因素隶属度D。

(11)

至此，完成了考虑直流偏磁影响的变压器状态分析及量化评价的模型建立工作。

4 实例分析

选取距离某2座特高压直流换流站100 km范围内的220 kV变电站，该变电站的变压器中性点采用直接接地方式，其型号为SSZ11-180000/220，变压器结构均为三绕组有载调压变压器，额定容量为180 000/180 000/90 000 kVA，额定电流为386.9 A，空载损耗为82.3 kW，负载损耗为450 kW，正常运行振动加速度为4.2 m/s2，连接组别为YNyn0d11。该变电站投运于2016年5月25日，从投运至今已产生了多次因直流偏磁而导致的变压器异常运行的情况。

选用三相式结构的相关数据为例，代入初始条件后，按照不考虑直流偏磁影响和考虑直流偏磁影响的变压器状态量化对比评价，其中D1、D2分别为不考虑直流偏磁影响和考虑直流偏磁影响的评价结果，可得结果如表4所示。

由表4评价结果可以看出，当考虑直流偏磁影响时，预测状态与实际状态相吻合，而不考虑影响时存在与实际状态不符的情况，如样本5—6、样本10—12都出现了状态转换。其中样本6和样本10由注意状态转变为异常状态，样本5和样本12由正常状态转变为注意状态。同时由样本6和样本10以及样本5和样本12评价结果的量化对比可以看出，当考虑直流偏磁转变成异常状态时，增加了36%的影响(影响量化结果以表3的状态上限分数为基准，求取各个样品的误差并取平均值，下面影响计算思路相同)，当转变成注意状态时，增加了21%的影响，因此可以说明的是考虑直流偏磁对变压器的状态评价结果影响显著。

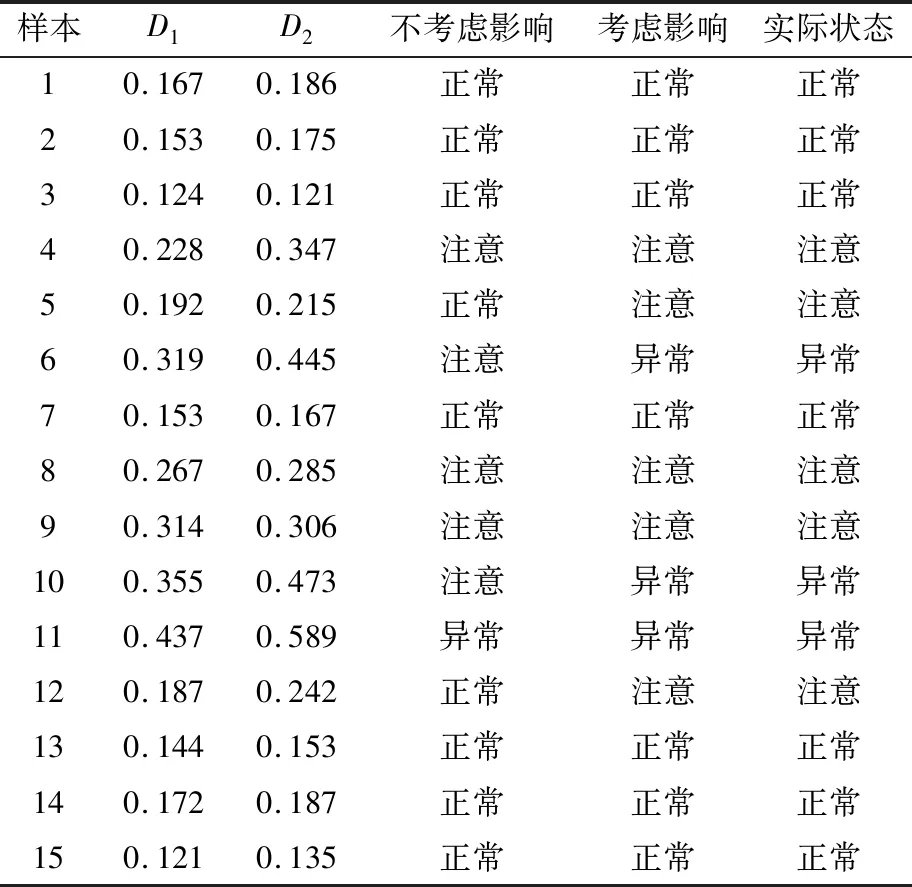
表4 变压器状态评价结果1

另外在考虑直流偏磁的基础上，以人工法和数据拟合法确定系数为自变量对变压器状态进行对比评价，其中D3、D4为人工法和数据拟合法评价结果，其结果如表5所示。

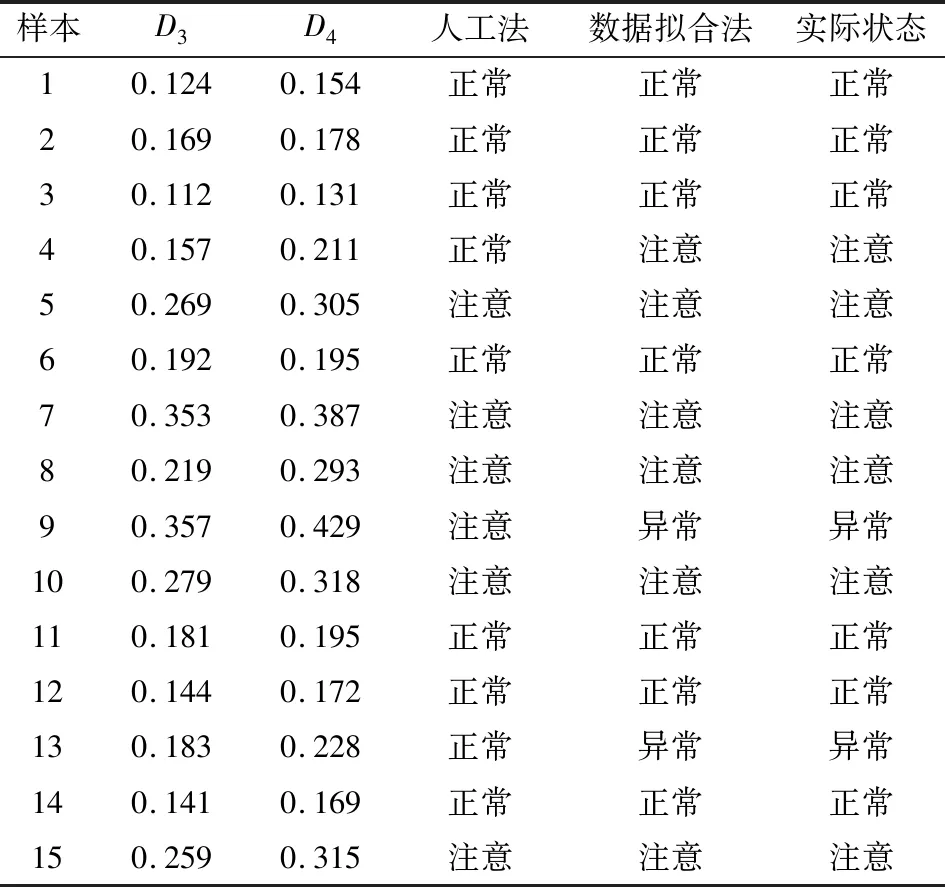
表5 变压器状态评估结果2

由表5的评价结果可以看出，当选择数据拟合法时，预测状态与实际状态相吻合，而用人工法时存在与实际状态不符的情况，如样本4、样本9、样本13发生了状态转变，其中样本4和样本13由正常状态转变为注意状态，样本9由注意状态转变为异常状态。对样本4和样本13以及样本9评价结果进一步量化，当采用数据拟合法时，正常状态转变成注意状态时增加了29%的影响，注意状态转变成异常状态时增加了20%的影响。由此，可以证明的是数据拟合法更符合实际状态，且比人工法能更加优越地对变压器状态量化评价。同时，可以给运行维护人员提供有效信息，注意变压器状态，合理安排检修计划。

由于所采用的数据为220 kV变电站数据，其数据范围可能具有局限性，因此，通过采集靠近换流站的另一220 kV变电站和某110 kV变电站数据用所提方法进行分析验证(35 kV因其电压等级较低，受影响小，因此不考虑该电压等级)，结果如表6所示，其中D6为220 kV评价结果，D7为110 kV评价结果。

表6 变压器状态评价结果3

由表6可以看出，220 kV变压器的评价结果与实际状态相比，有2个出现了状态转换，即出现2个未能成功评价的样本，其成功评价率为86.67%。具体来说，未成功评价的样本6和样本8评价结果与所定义的状态量化指标相比，其平均误差率为8.375%，由此可知所提方法在相同电压等级下的评价效果较好。同样地，110 kV变压器出现3个未能成功评价的样本，其成功评价率为80%。具体上，未成功评价的样本1、样本9和样本15评价结果与所定义的状态量化指标相比，其平均误差率为2.68%，由此可知所提方法在不同电压等级下的评价效果同样较好。因此，可以得出所提方法在不同电压等级下的状态评价同样适用，工程应用性较强。同时，由上述仿真分析可知，通过把2座变电站的实际状态数据代入所提模型，判断变压器状态，其判断结果与实际运行状态相一致，可以说明的是所采用的状态划分标准是合理的。

在上述仿真的基础上，分析所提方法对不同内部结构变压器的适用情况。仿真结果如表7所示，其中D4、D8分别为三相式和单相式结构评价结果。

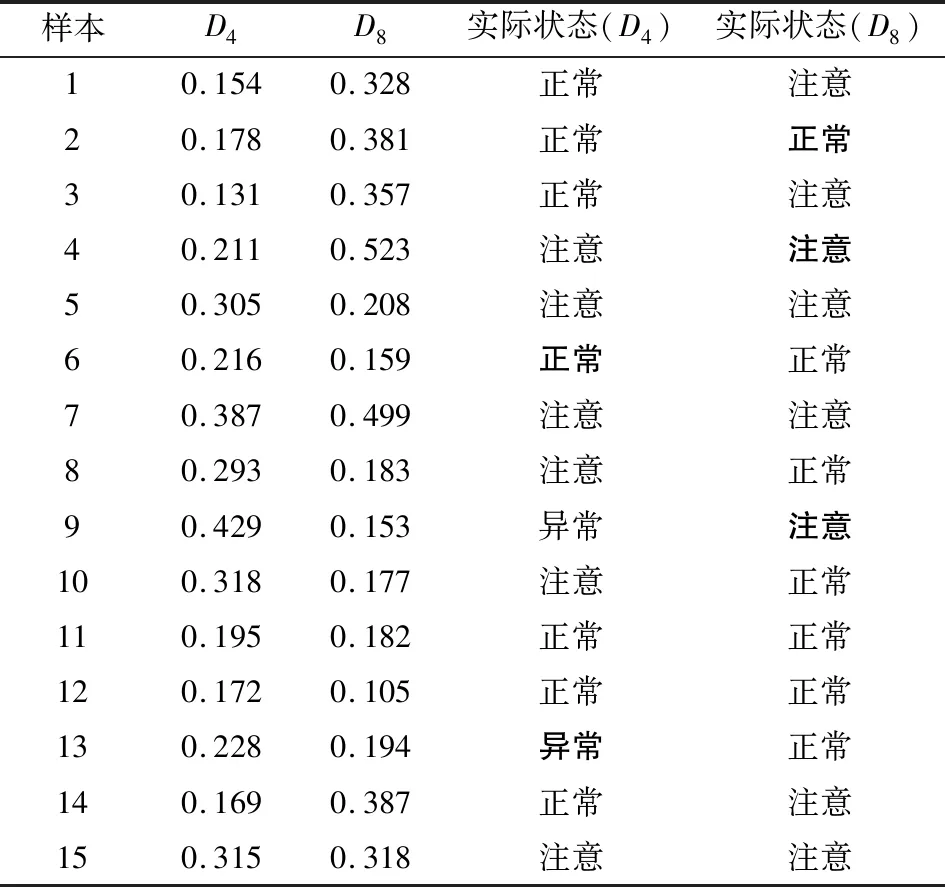
表7 变压器状态评价结果4

由表7可以看出，三相式和单相式评价结果分别存在2个和3个未能成功评价的样本，其成功评价率分别为93.33%和96.67%。具体说，三相式结构变压器未成功评价的样本13与所定义的状态量化指标相比，其平均误差为25.5%；单相式结构变压器未能评价的样本2、样本4和样本9的平均误差为48.25%。由此可知，所提方法对不同结构的变压器有较好的适用性，但相对于单相式结构变压器，所提评价方法更适合于三相式变压器。

5 结 论

从直流偏磁的原理出发，通过考虑直流偏磁对换流站附近变电站变压器的影响并进行了量化评价，有如下结论：

1)从直流偏磁的角度，分析了直流偏磁对变压器噪声、振动强度和损耗的影响，给出了考虑直流偏磁的量化表达式和相应模型。

2)为了避免人工经验的主观性，采用数据拟合的方式确定模型中的待定系数，由实例仿真可知，采用数据拟合的方式能显著提高预测精度，更加准确地预测变压器的状态。

3)采用模糊评价法对模型进行仿真验证，与不考虑直流偏磁影响和采用人工法确定系数的模型对比，得到了考虑直流偏磁影响和采用数据拟合法的模型更加符合变压器实际状态；同时所提方法对不同电压等级和不同结构的变压器状态评价具有普适性，工程应用性好，使运行维护人员能更加高效地制定检修计划，提升了工作效率。