基于BFO-LSSVM模型的爆破料级配预测研究

余良松 赵伦 彭勇 惠红强

摘要：为实现爆破级配曲线的准确预测，借助细菌觅食算法（BFO）及最小二乘支持向量机（LS-SVM）理论构建基于BFO算法的LS-SVM优化模型（BFO-LSSVM）。使用35组爆破数据作为训练样本对模型预测精度进行检验，选取孔排距、堵塞、孔深等因素作为输入因子，爆破料级配作为预测模型输出因子。结果表明，BFO-LSSVM预测模型的预测结果精度高于相同样本容量下LS-SVM模型。以阿尔塔什水利枢纽工程料场开挖爆破数据为例，BFO-LSSVM模型预测结果平均误差为1.47%，验证了该预测模型的可行性及实用性。

关键词：爆破级配;块度预测;最小二乘支持向量机;细菌觅食算法

随着我国经济的不断发展，基础建设也随之不断扩大，越来越多的不同尺寸的石料被广泛的运用于水利工程（堆石坝、防洪堤）、建筑等工程。钻孔爆破是石料开采的主要手段之一，其中爆破块度及其大小分布是评价石料开采爆破优劣的主要参数之一，爆破块度过大会导致二次破碎成本增加以及增大运输难度。另一方面，在堆石坝填筑时，爆破块度的级配也会对坝体的密实度产生直接影响。

目前，国内外科研工作者针对爆破块度分布进行了大量研究，提出了众多计算理论及预测模型。如武仁杰和李海波等基于多元回归分析方法建立了块度预测模型，并通过对比实测爆破跨度统计数据，验证了该预测模型的正确性;李瑞泽等利用三维激光扫描技术对爆破碎石颗粒形状及表面积开展了详细研究。Cunninghan综合考虑爆破参数、岩体性质及炸药单耗等因数条件下，利用Kuznetsov方程与R-R方程相结合的方法对X50展开了研究。吴新霞等结合实际工程背景，在Kuz-Ram模型基础上研究并提出了适用于天生桥以及水电站筑坝级配料预测模型。

传统预测方法由于输入参数较少，且依赖于特定条件下爆破实测数据，因此建立的爆破块度预测模型通用性较差。随着计算机科学的发展，利用计算机处理能力分析预测爆破块度也得到了广泛运用，如遗传算法、支持向量机法、神经网络法等。王泽文等綜合考虑装药工艺、岩体性质及爆破参数等影响因素，建立了基于PSO-ELM的爆破块度预测模型。史秀志等基于最小二乘支持向量机思想，构建了适用于小样本条件下的预测模型。

综上所述，综合考虑岩体性质、炸药类型、爆破参数等因素，实现岩体爆破后块度的预测已成为岩体爆炸力学领域热点问题之一，并取得了一定得进展。但现有基于经验公式法建立的预测模型考虑因素较少，且人工神经网络法预测结果受隐含层节点数影响较大，学习效果较差。

基于此，本文依托实测爆破数据，将细菌觅食算法（BFO）引入到最小二乘支持向量机（LSSVM）中，利用细菌觅食算法全局搜索能力强等特点优化最小二乘支持向量机参数，构造BFO-LSSVM爆破块度预测模型，进而实现爆后级配曲线的准确预测。

1 最小二乘支持向量机算法

1.1 支持向量机

支持向量机（Support Vector Machine）是由Vapnik等提出来的一种二级分类模型。SVM具有模型精度较高，适应能力优良，并且有着优秀的鲁棒性以及泛化能力等特点。在爆破块度的结果预测中，因为影响块度分布的因素众多，利用SVM方法通过选择映射函数（核函数）将块度分布的结果与岩体性质、炸药类型、爆破参数等多影响因素之间的非线性关系映射成为高维空间的线性关系，进而实现爆破块度的准确预测。

1.2 最小二乘支持向量机

最小二乘支持向量机（Least Squares Support Vector Machine）是一种针对SVM的改进算法，通过将比较目标函数误差的平方项结果作为算法的优化评判标准，并将计算过程中的约束条件变为等式约束达到降低求解难度、提高求解效率等目的。基本原理如下：

对于样本，采用与支持向量机相同的算法理论，构造出最小二乘支持向量机的目标函数为：

2 BFO-LSSVM爆破块度预测模型的建立

2.1细菌觅食优化算法（Bacteria Foraging Optimization）

细菌觅食优化算法是2002年由Passion基于大肠杆菌的觅食行为提出的一种智能优化算法，大量数据分析表明，该算法具有全局搜索能力强、鲁棒性强等优点。该算法根据觅食的四个基本行为（趋向性、聚集性、复制性和迁徙性）求解工程问题。

（1）趋向性：大肠杆菌的觅食过程中有两个动作：旋转和游动。旋转是为了找到一个新的方向运动，而游动则是继续按照之前的方向运动。趋向性操作的本质就是对这两个动作的模拟。

式中：表示细菌i在第j次趋化第k次复制第l次驱散后的位置。

（2）聚集：细菌觅食过程中，不同个体存在斥力与引力两种作用力，其中斥力使细菌在一定区域内单独觅食，引力则使细菌向特定区域聚集。其聚集的数学表达式为：

（3）复制：细菌进化过程服从优胜劣汰原则，其中觅食能力强的细菌进行复制。表达式为：

（4）迁徙：当细菌所处坏境发生突变时，算法给定一定概率模拟细菌迁徙过程，使细菌个体在概率死亡条件下产生一个新个体，该行为有利于算法跳出局部最优解。

2.2 基于BFO优化的LSSVM模型

采取基于BFO算法优化LS-SVM参数，运用经过优化后的LS-SVM来对爆破块度的分布进行预测。首先读取爆破块度的数据，把数据分为训练样本和预测样本，然后利用BFO算法计算出LS-SVM的最优参数，再将获得的最优参数的值代入LS-SVM中对训练样本进行训练，最后对预测样本进行分析，计算出相对应的结果。

算法的流程图如下所示：

2.3 不同预测模型对比分析

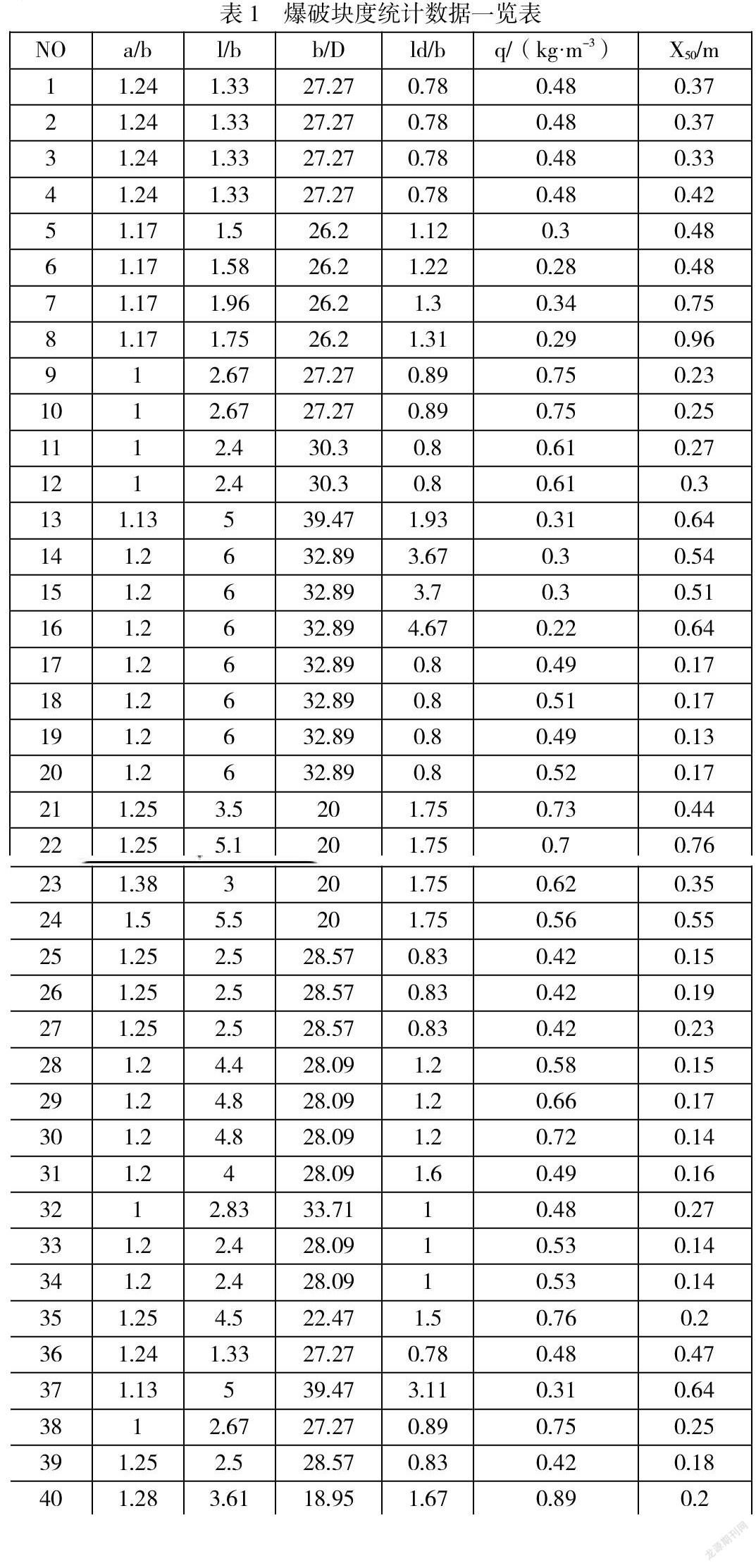
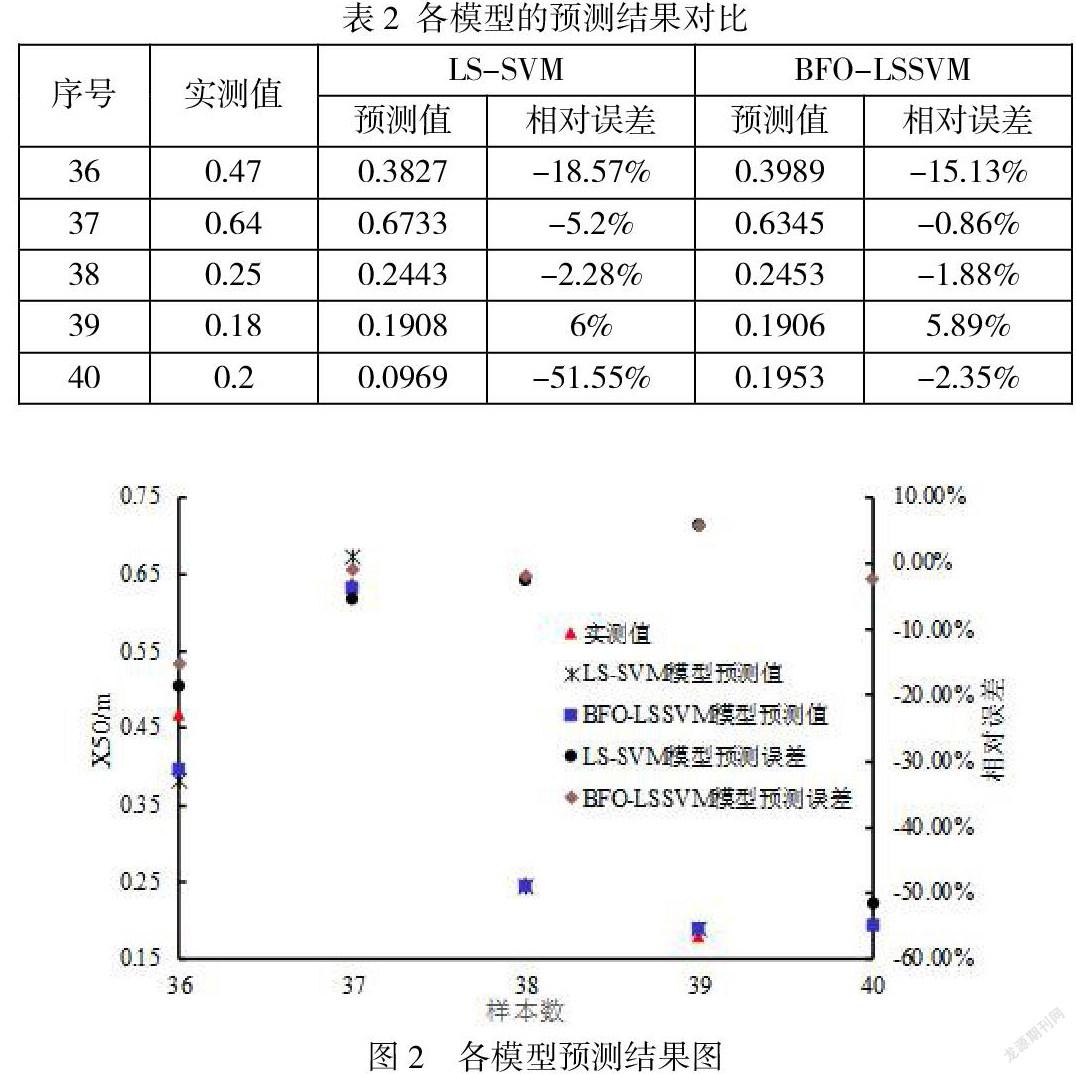
取40组文献中的露天矿山爆破块度统计数据，其中前35组数据为训练样本，后5组为模型预测精度验证测试样本，取相对误差及平均绝对误差作为计算指标，用来评估LS-SVM、BFO-LSSVM预测模型的预测精度。爆破块度统计数据见表1。各模型预测结果见表2及图1。

从表2可以看出，两种不同预测方法的平均绝对相对误差分别为16.72%和5.22%。由图2可知，BFO-LSSVM模型的拟合度较高，除了第一组的预测值相对误差稍大，另外四组预测结果相当好;反观LS-SVM模型，预测的稳定性不高，存在个别预测样本值误差过大的问题。综上可知，由BFO优化后的LSSVM模型比原模型有更高的预测精度，且数据拟合能力更强。

3 工程案例分析

3.1 工程概况

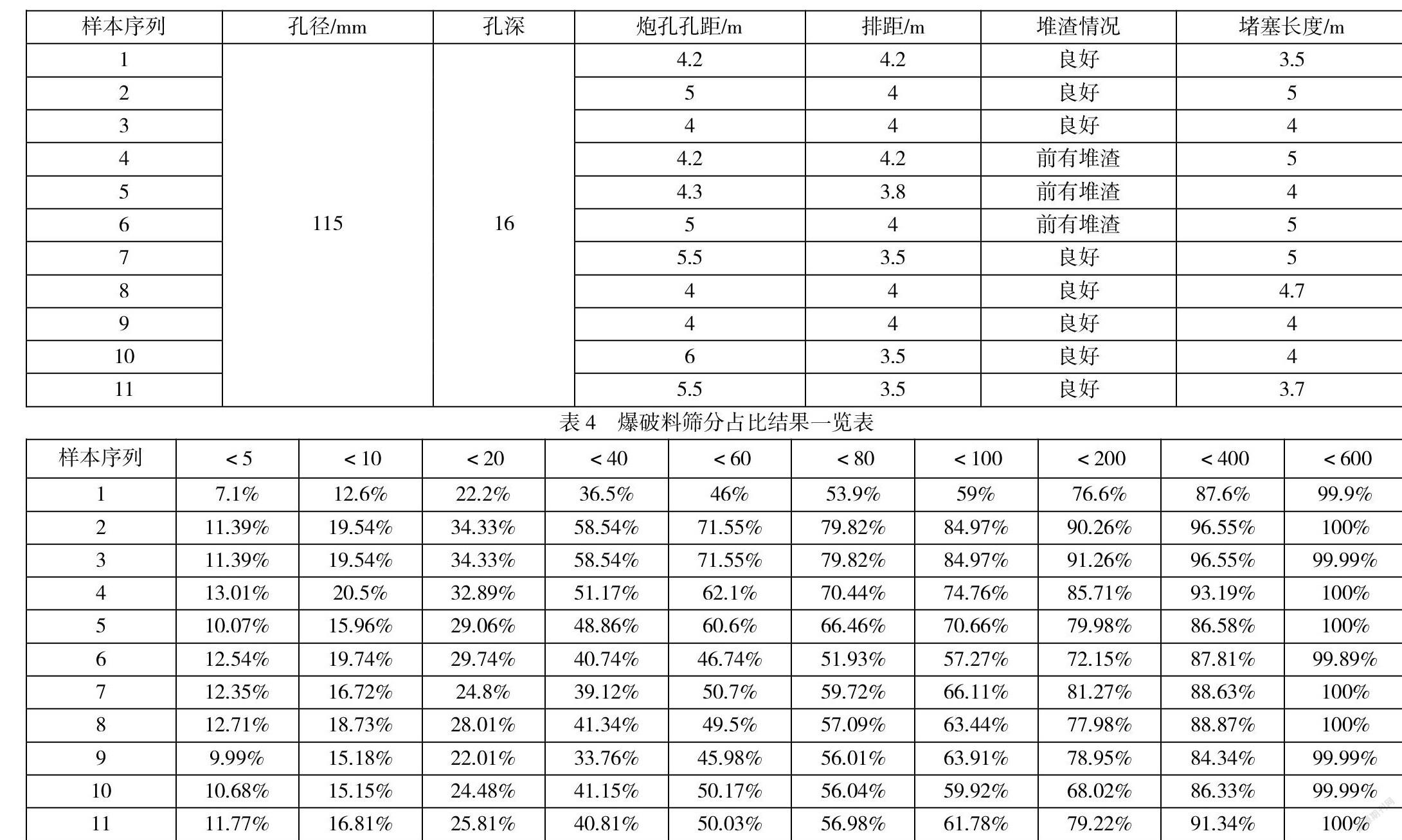
阿尔塔什水利枢纽工程位于喀什地区莎车县和克孜勒苏克尔克孜自治州阿克陶县交界处，是叶尔羌河干流山区下游河段的控制性水利枢纽工程，是叶尔羌河干流梯级规划中“两库十四级”的第十一个梯级，规划水库正常蓄水位1820米，最大坝高164.8米，水库总库容22.49亿立方米。为满足工程大坝浇筑过程中用料需求，现场需进行爆破试验。通过爆破试验对参数进行调整，以保证料场开挖所提供的石料级配满足设计要求。根据现场交通及岩体出露状态，选取P1料场开挖区11组实测爆破料筛分数据，爆破参数如表3所示，各次爆破料筛分结果见表4。选组前10组作为训练样本，剩余1组作为预测样本。

3.2 预测结果分析

通过爆破试验，获取石料开挖爆破料粒径筛分结果，结合现场各次爆破试验相应爆破设计参数，通过建立的BFO-LSSVM预测模型，进行爆破料块度级配预测，并与实测值分析比较。

（1）根据前10组训练样本爆破料筛分结果，结合对应爆破试验参数，用BFO-LSSVM进行训练，确定BFO算法的参数值，如表所示。通过对训练样本数据的爆破料粒径与爆破参数分析可知，爆破料粒径大小与爆破孔网参数成正相关，即爆破料大小随孔网参数增加而增大。

（2）根据所建立的BFO-LSSVM预测模型，基于前10组训练样本进行训练的基础上，对第11次爆破料级配进行预测，预测结果如表5所示。

从表5中可以看出，爆破料级配的预测结果依次为10.9、16.89、28.13、42.54、52.8、54.82、59.86、78.88、88.82、99.97。将预测结果与实际结果进行对比分析可以看出，BFO-LSSVM模型预测结果最大误差仅为2.52%，平均误差为1.47%，预测结果误差控制的相当小，能满足工程实际的需求。

结语

（1）基于最小二乘支持向量机构理论，构造了基于BFO-LSSVM的爆破块度预测模型。通过LS-SVM模型和BFO-LSSVM模型的预测结果对比，结果表明，BFO算法可在一定程度上对LS-SVM模型的性能进行优化，使误差从16.72%降低到5.22%，即BFO-LSSVM模型在爆破料级配的预测中具有比LS-SVM模型更高的预测精度。

（2）基于BFO-LSSVM块度预测模型对阿尔塔什水利枢纽工程堆石料开采过成中收集的爆破料级配数据进行了级配曲线的预测，其预测平均误差为1.47%，进一步证明了在确定的爆破参数和现场岩体条件下，爆破料级配预测的可行性，对坝料的控制开采具有重大的意义。

（3）基于小样本对爆破料级配预测时，训练样本数据的准确性对模型预测结果的精度有较大的影响。同时BFO-LSSVM模型应用过程中没有考虑结构面对爆破块度的影响，使得文中模型的预测结果只适用于岩性相同或相近的料场。

参考文献（References）

[1]梁向前，傅海峰. 面板堆石坝坝料爆破开采技术研究进展[J]. 水利规划与设计，2007，5：71-73.

[2]Norazirah A，Fuad S，Hazizan M. The Effect of Size and Shape on Breakage Characteristic of Mineral[J]. Procedia Chemistry，2016，19：702-708.

[3]朱晟，宁志远，钟春欣，等. 考虑级配效应的堆石料颗粒破碎与变形特性研究[J]. 水利学报，2018，49（7）：849– 857.

[4]武仁杰，李海波，于崇，等. 基于统计分级判别的爆破块度预测模型[J]. 岩石力学与工程学报，2018，37（1）：141-147.

[5]李瑞泽，卢文波，尹岳降，等. 白鹤滩旱谷地灰岩爆破碎石颗粒形状及比表面积特征研究[J]. 岩石力学与工程学报，2019，38（X）：1-11.

[6]Cunningham C. 预估爆破破碎的KUZ-RAM模型[J]. 第一届爆破破岩国际会议论文集，长沙岩石力学工程技术咨询公司编译，1985：251-257.

[7]吴新霞，彭朝辉，张正宇，等. Kuz-Ram模型在堆石坝级配料开采爆破中的应用[J]. 长江科学院院报，1998，4：40-42+46.

[8]祝文化，朱瑞赓，夏元友. 爆破块度预测的神经网络方法研究[J]. 武汉理工大学学报，2001，1：60-62.

[9]郝全明，杨振增. BP神经网络在岩层爆破参数优化中的应用[J]. 煤炭技术，2014，33（12）：20-22.

[10]王泽文，左宇军，赵明生，等. 基于PSO-ELM的爆破块度预測研究[J]. 矿业研究与开发，2019，39（06）：136-139.

[11]史秀志，王洋，黄丹，等. 基于LS-SVR岩石爆破块度预测[J]. 爆破，2016，33（3）：36-40.

作者简介：余良松（1976年7月—），男，汉，浙江杭州人，硕士，高级工程师，研究方向：水利水电工程施工。