基于加权组合模型的地下水水位拟合

陈 晶，水青娜，王俊智，田光辉，王心义

（1.河南理工大学 资源环境学院，河南 焦作 454000；2.上海亚新建设工程有限公司，上海 201900；3.天津地热勘查开发设计院，天津 300250）

0 引言

地下水水位作为指示地下水资源时空变化的关键要素，其依据监测资料进行的精准拟合一直是水文地质领域关注的热点［1］。但受气象、水文、地貌、地质和人为活动的影响，精确模拟地下水位是比较困难的［2］。

目前，模拟地下水水位变化的常用方法有数值模 拟 法［3-5］、时 间 序 列 分 析 法［6］、神 经 网 络 模 型［7-11］、灰色系统GM（2，1）模型［12］、泊松曲线模型［13］、指数曲线模型［14］等。数值模拟法具有精细化仿真和快速自动计算的优点，但由于拟合时需要的参数多，在资料欠缺的情况下，难以精确刻画地下水位；时间序列分析法需要较多的数据，且操作难度高、计算量大；神经网络模型模拟法需要的拟合周期比较长，计算时收敛速度慢，工作效率低，且存在局限性［15］。灰色理论模型模拟法对数据长度要求相对不高，因此当地下水位年际变化较大时，该模型的准确度也不太高［16］。灰色系统GM（2，1）模型模拟法的初期拟合结果具有较高的拟合度，但中后期拟合结果精确度显著降低；指数曲线模型模拟法拟合结果与灰色系统GM（2，1）模型相反。

Bates针对各种地下水水位模拟方法的局限性，以航空客运数据为例，构建了客运预测的组合模型，经计算，组合模型的均方误差远小于单一模型的［17］。笔者综合灰色GM（2，1）模型和指数曲线模型的优点，基于最优赋权法，构建了地下水水位拟合的加权组合模型，并以巩义市某煤矿长观孔地下水水位监测资料为样本，应用3种模型进行了水位拟合，以期为地下水水位的精准拟合提供技术支持。

1 模型构建

1.1 数曲线模型

地下水水位具有自相关性，因此常用指数曲线模型来拟合，其基本方程为式（1）［18］。

式中：t为观测时间，d；St为t时的拟合水位，m；S∞、a和b为待定系数。

选取3个时间点t1、t2和t3，且t3-t2=t2-t1=Δt，可列式（2）。

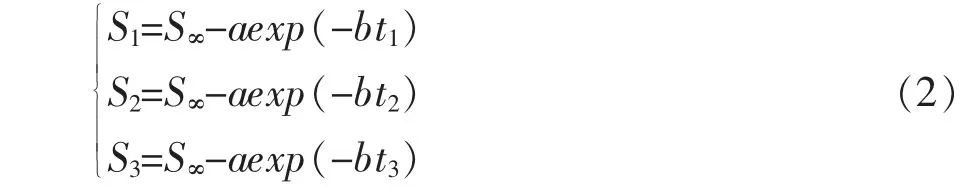
当Δt尽可能大时，可得出3个待定系数的表达式如式（3）所示。

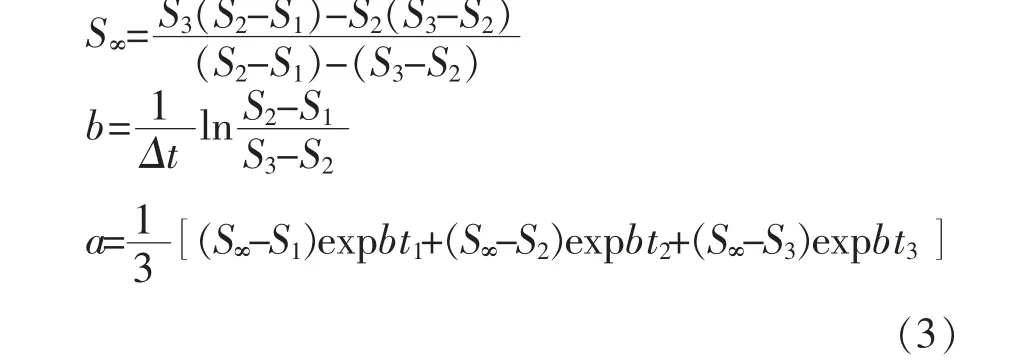
计算出S∞、a和b，即可得到指数曲线模型的表达式。

1.2 M（2，1）模型

灰色拟合模型是针对拟合对象的不确定性，根据少量已知信息进行二次开发，实现对系统运行规律的正确描述和有效控制的数学模型［19］。GM（2，1）模型是一个包含二阶方程和一个未知量的灰色模型，它基于一组有明显指数规律的生成数来构建二阶微分方程，再利用方程通解来描述生成数的变化规律，这一过程通常称为白化过程［20］。

1.2.1 本理论

设 X（0）=｛x（0）（1），x（0）（2），…，x（0）（N）｝为GM（2，1）模型的原始数列，对其进行一次累加，结果如式（4）所示［21-22］。

将累加生成的序列X（1）分别作两次累减，一次累减结果如式（5）所示，二次累减结果如式（6）所示。构建如式（7）和式（8）所示的矩阵X（A，B）和YN。

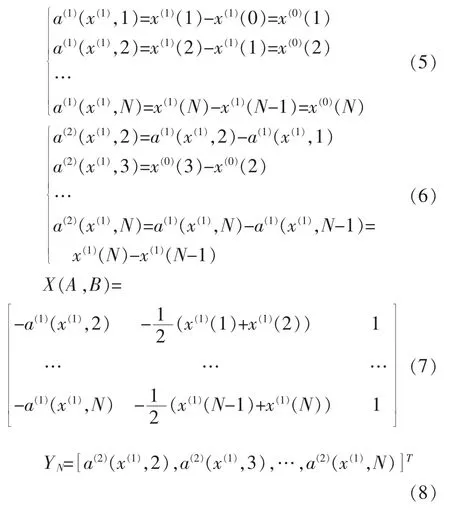
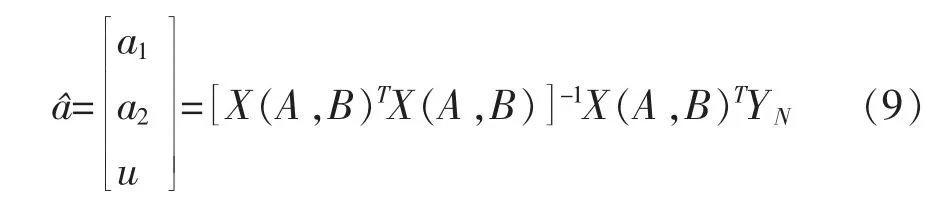
基于系数向量构建的系统响应方程如式（10）所示，其解为式（11）。

令Δ=a12-4a2。

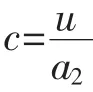
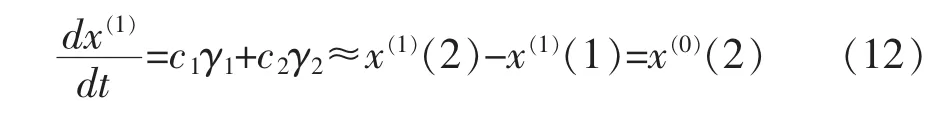
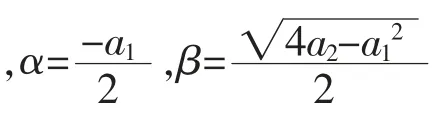
1.2.2 靠性分析

构建的GM（2，1）模型是否可靠，可以通过对拟合值的检验来确定。一般的检验方法有关联度检验法、后验差检验法和残差检验法，通常使用后验差法进行检验［25-26］。后验差法的检验步骤为：

（1）根据式（14）计算离差［27］。

（2）根据式（15）计算残差的离差。

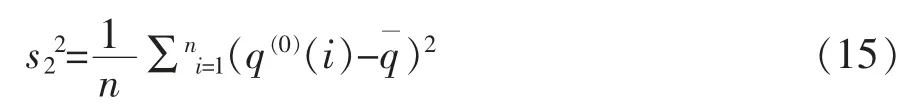
其中，q（0）（i）=x（0）（i）-＾x（0）（i）。

（3）根据式（16）计算后验差c及小误差概率p［28］。

c值越小，说明拟合误差离散越小；p值越大，说明模型误差较小的概率越大。GM（2，1）模型可靠性评价标准列于表1。

表1 GM（2，1）模型可靠性分级Tab.1Reliability classification of GM（2，1）model

1.3 权组合模型

加权组合模型是指针对同一拟合对象，利用不同的权重将各单一模型结合起来［29］，以充分利用单一模型的优点，提高模型的拟合度和精确度。

1.3.1 型构建

假设某一拟合对象为f=y（f1，f2…，fk），第i种方法在t时刻的拟合结果为fit（i=1，2，…，k），k种方法在组合模型中所占的权重系数向量W=（w1，w2，…，wk）T，则组合模型拟合结果为式（17）［30］。

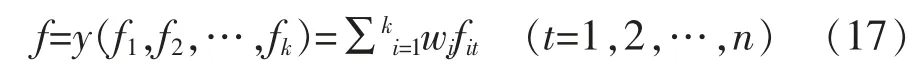
确定组合权重系数常用的方法有递归方差倒数法、最优加权法、方差-协方差法，本文采用最优加权法（拟合误差平方和最小）来获得权重系数向量［31］。

记组合模型的拟合误差为et，其平方和为J，则有式（18）所示的联立方程。

组合模型的加权系数可利用最小二乘法求得，如式（19）所示。

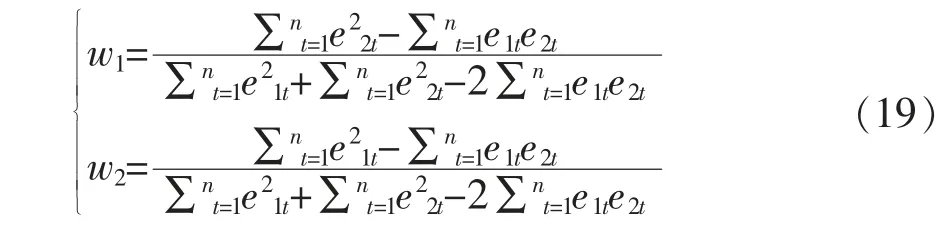
其中，e1t和e2t分别是单个模型的拟合误差。

1.3.2 法比对

通常采用误差平方和SSE、平均绝对误差MAE、平均绝对百分比误差MAPE3种参数评价拟合方法的优劣［32］。3种参数的计算式如式（20）～式（22）所示。其中，frt为实际测试的t时刻值，fjt为某种方法拟合的t时刻值。

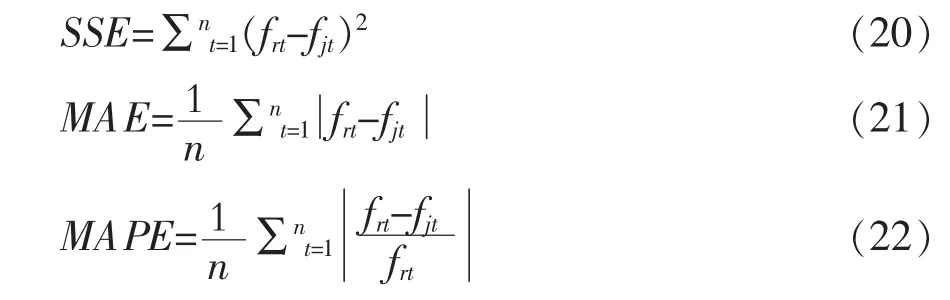
2 模型应用

2.1 合结果

以巩义市某煤矿水文观测孔2012～2018年的水位观测值为样本，并以6个月为一个周期，分别采用指数曲线模型、GM（2，1）模型和加权组合拟合模型（基于最优加权法，得到的加权组合模型为：fj=0.31j1+0.69j2）进行水位拟合。由于地下水水位是负值，为便于计算，采用水位埋深来表征水位变化。拟合结果及误差如表2和图1所示。

由表2可知，GM（2，1）模型的误差最大值和平均值分别为3.98 和1.93 ，指数曲线模型的误差最大值和平均值分别为2.08 和-0.63 ，加权组合模型的误差最大值和平均值分别为1.46 和0.13 m。显然，组合模型误差小于单一模型。

由图1可以看出，GM（2，1）模型拟合结果在前期与实际水位曲线保持一致，但是后期与实际水位曲线偏差较大；指数曲线模型拟合结果不能真实反映水位的实际变化；组合拟合模型拟合结果曲线与水位实际曲线变化趋势基本一致，拟合精度较高。

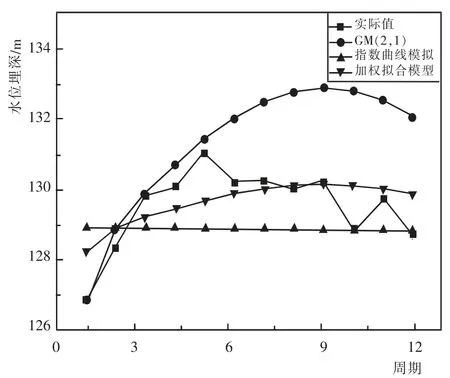
图1 模型的模拟值与实测值对比Fig.1Comparison of simulation values and measured values of model

2.2 果讨论

利用式（20）～式（22）可分别计算3种拟合方法的误差平方和SSE、平均绝对误差MAE、平均绝对百分比误差MAPE，结果如表3所示。

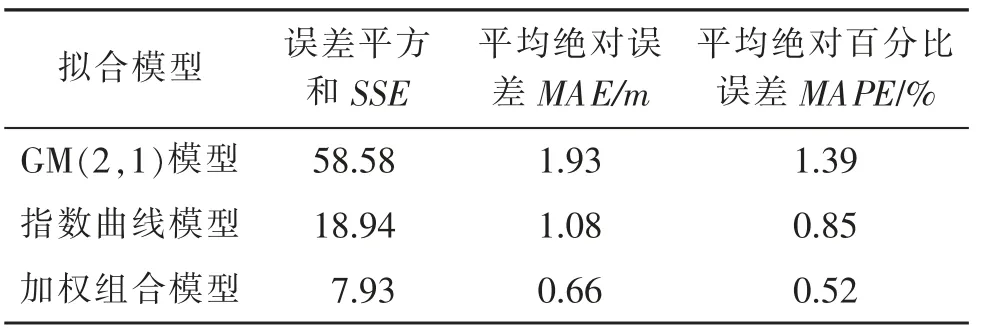
表3 不同模型的拟合误差Tab.3Fitting errors of different models

表3显示，相较于指数曲线模型和GM（2，1）模型，组合拟合模型的误差平方和SSE降低了50.65 和11.01 平均绝对误差MAE降低了1.27 0.42平均绝对百分比误差MAPE降低了0.87 和0.33 。这表明，组合模型的精度最高。组合模型综合了单一模型的优点，降低了拟合误差，为地下水位拟合提供了一种新方法。

3 结语

综上所述，笔者针对地下水位埋深的时空多变性和自相关性，以灰色系统GM（2，1）模型和指数曲线模型为基础，基于最优加权法构建了组合模型。实例证明，组合模型拟合结果与实际水位曲线变化趋势基本一致，拟合精度高于单一模型。组合模型克服了单一拟合模型的局限性，为提高地下水水位的精准拟合提供了可借鉴的方法。