基于wiener过程的唇形密封圈剩余寿命预测模型研究

陈启航，孙灏，孙成

（中国船舶重工集团公司第七二三研究所，扬州 225001）

引言

唇形密封圈作为一种常见的动密封件，使用寿命长达近1 000 h。考虑到其结构简单的特点，许多学者从有限元仿真出发，进行各类失效模式的物理建模，并结合多场耦合分析，得到密封圈在单一失效模式下的寿命预测模型。但随着工况环境的日益复杂，考虑单一失效模式建立得到的密封圈剩余寿命预计模型精度并不高。本文采用贝叶斯模型法，在工况下采集得到唇形密封圈的退化数据，包括摩擦扭矩和泄漏率，并根据历史寿命数据和退化数据特点选定基于wiener过程的退化模型[1]，再结合实时的退化数据进行模型参数的更新求解，得到唇形密封圈的剩余使用寿命可靠性评估。

1 剩余寿命预测模型

1.1 基于wiener过程的模型假设

目前，基于数据驱动的寿命预测模型类别主要有基于轨道、基于累计损伤和基于随机过程等[2]。唇形密封圈的工况环境复杂，在使用过程中，其性能参数的采集会存在误差，且其中一个性能参数：摩擦扭矩值，具有数量级小、随环境波动性大等特点，采集得到的退化量数据通常不是严格单调递增的，因此，本文采用基于随机过程退化模型中的wiener过程进行建模。

假设唇形密封圈的性能参数退化规律服从wiener过程[3]。采用贝叶斯法，结合试验过程中新获取的退化数据，更新唇形密封圈退化模型中的参数，建立其剩余寿命预测模型。具体流程如图1所示。

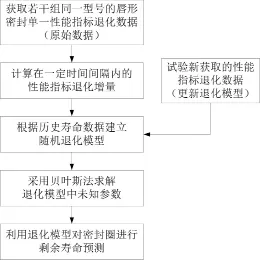
图1 密封圈剩余寿命预测模型流程图

令{Xi(tj)；tj≥0}为唇形密封圈的性能指标退化过程，用wiener过程可描述为：

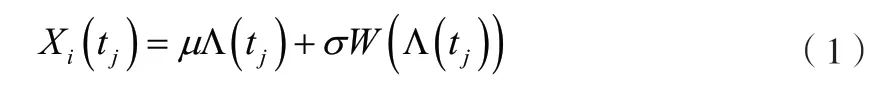
式中：

{Xi(tj)； tj≥0}—第i个唇形密封圈样本性能指标在第j个测量时间点tj时的退化量，i>0，j≥0；

W(·)—标准布朗运动；

Λ(t)=tjq—时间尺度函数；

µ—漂移系数；

σ—扩散系数。

wiener过程中，认为一系列唇形密封圈的性能指标在一定时间间隔内的退化增量，都满足正态分布[4]。其性能指标的退化增量表达如下：

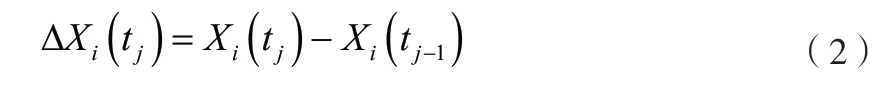
式中：

ΔXi(tj)—第i个唇型密封性能指标样本在时间间隔(tj-1, tj)内的退化增量。

性能指标的退化增量满足正态分布，即：

式中：

ΔΛ(tj)=tjq-tj-1q，Xi(tj-1)—第i个唇形密封圈样本的性能指标在第j-1个测量时间点tj-1时的退化量。

1.2 贝叶斯模型参数求解

为求解唇形密封圈的退化模型中的参数，用贝叶斯方法，结合先验信息估计出似然函数中的未知参数。这里采用Openbugs软件通过马尔可夫链蒙特卡洛（MCMC）方法来计算未知参数，先验分布为无信息的先验分布。这里的未知参数为：µ，σ，q。使用Openbugs软件求解未知参数的部分代码见图2。

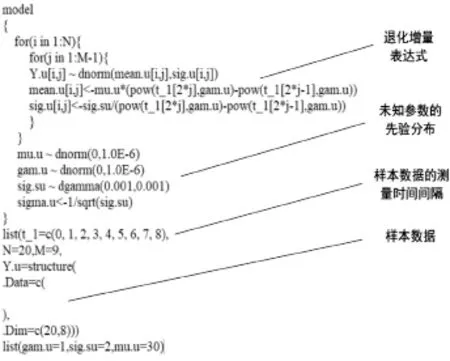
图2 Openbugs求解参数代码图

需要注意的是，若在后续的参数监测过程中，获取了新的样本数据，可以对原有的模型进行更新改进，更新其先验分布值，进而对唇形密封圈的退化模型进一步更新。

1.3 唇形密封圈寿命可靠度模型

在得到参数估计后，进一步求解唇型密封性能指标的累计分布函数，公式如下：

式中：

T—基于退化过程{X(t)；t≥0}的寿命，且T=inf{t |X(t)≥ω}；ω—对应性能指标的阈值。

最后利用可靠度函数计算唇形密封圈的剩余寿命可靠度。公式如下：

2 退化数据采集

2.1 摩擦扭矩采集

这里对某型号的唇形密封圈进行全寿命周期的试验，在一定工况条件下，进行性能参数实时监测采集，参数包括摩擦扭矩和泄漏率。

该密封圈的摩擦扭矩值采用实时监测采集的方式，通过与转轴连接的扭矩传感器实时采集唇形密封圈的摩擦扭矩值。

在测量中，需要考虑的是该密封圈的摩擦扭矩值数量级为在0.1 Nm，且在整个寿命周期试验过程中退化趋势并不明显，在测量过程中非常容易受到环境干扰。因此，在获得原始数据后需要对其进行滤波处理。

得到一定工况下，该型号唇形密封圈全寿命周期的摩擦扭矩原始数据值统计，如图3所示。

图3 全寿命周期摩擦扭矩数据图

2.2 泄漏率采集

唇形密封圈的泄漏率采用单位时间内离散测量泄漏量的方法，在一定单位时间内收集试验密封圈底部泄漏的油液，再用精密的天平对该时间段内的油液泄漏量进行测量，得到该段时间内的泄漏率。

得到一定工况下，该型号唇形密封圈全寿命周期的的泄漏率数据值统计，如图4所示。

图4 全寿命周期泄漏率数据图

3 唇形密封圈剩余寿命可靠性分析

3.1 唇形密封圈寿命预测模型

在相同工况条件下，根据历史失效数据和专家经验可以得到该型号唇形密封圈的泄漏率和摩擦扭矩的失效阈值（见表1），并通过历史使用寿命数据可以得到该型号唇形密封圈的平均使用寿命为935 h。

表1 某型号唇形密封圈退化失效阈值

根据唇形密封圈的退化模型可以得到该密封圈的寿命可靠性曲线，由此得到其平均使用寿命（MTTF），将其与历史数据得到的该型号密封圈平均使用寿命进行相对误差计算，得到模型的精度。这里将摩擦扭矩和泄漏率各选取10组采集数据，并选取8段区间的增量，进行唇形密封圈的可靠性分析。

让Xi(tj)表示为第i个唇型密封样本的性能指标在第j个测量时间点tj时刻的退化量。令退化增量表示为：

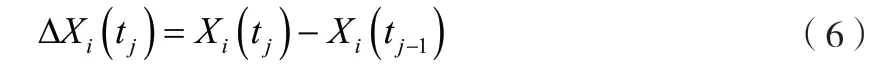
其中，i=1，2，…，10，j=1，2，…，8，且Xi(t0)=0。

对于i=1，2，…，10，退化增量均满足：

其中，ΔΛ(tj)=tjq-tj-1q。

再结合MCMC法进行后验分布的参数值估计。得到其唇形密封圈寿命模型的可靠性分布。

3.2 基于摩擦扭矩的剩余寿命评估

唇形密封圈的摩擦扭矩退化规律为在试验初期退化速度较快，在试验后期的摩擦扭矩波动性较大，但在总体均值区域较为平稳。

这里选取摩擦扭矩作为唇形密封圈的性能退化数据，通过选取一定的摩擦扭矩退化数据量，根据退化模型得到唇形密封圈的剩余寿命可靠性曲线（如图5所示）。

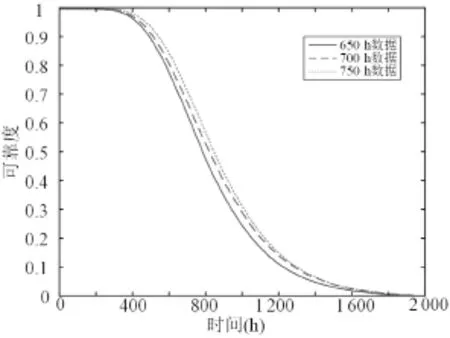
图5 基于摩擦扭矩的可靠度曲线

通过基于摩擦扭矩退化数据的唇形密封圈可靠度曲线，可以计算得到密封圈的平均使用寿命，将其与实际测量得到的寿命数据相对比，得到的预测精度如表2所示。

表2 基于摩擦扭矩的模型精度比对

3.3 基于泄漏率的剩余寿命评估

唇形密封圈的泄漏率退化规律为在试验初期无泄漏产生，根据试验数据，从510 h后唇形密封圈才逐渐开始产生泄漏量，因此这里在选取退化数据数量时选用偏后期的泄漏率退化数据，根据退化模型得到唇形密封圈的剩余寿命可靠性曲线（如图6所示）。

图6 基于泄漏率可靠度曲线

通过基于泄漏率退化数据的唇形密封圈可靠度曲线，可以计算得到密封圈的平均使用寿命，将其与实际测量得到的寿命数据相对比，得到的预测精度如表3所示。

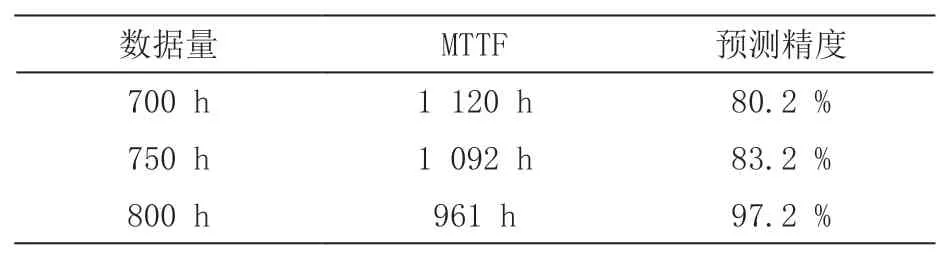
表3 基于泄漏率的模型精度比对

4 结论

本文提出了基于wiener过程的唇形密封圈贝叶斯模型剩余寿命预测法，利用对某型号唇形密封圈的性能参数进行监测采集，建立其退化模型，得到其剩余寿命的可靠性分布，主要有以下几点总结：

1）通过结合退化数据，解决了唇形密封圈使用寿命评估中遇到的工况环境复杂、失效形式多样等研究难点。

2）基于wiener过程的唇形密封圈剩余寿命预测模型在包含650 h以上的数据量时，精度均达到了80 %以上。

同时，针对该模型现有的数据结构，可以提出以下展望：

1）在唇形密封圈的退化数据分析中，可采用Copula函数建立两个退化变量之间的相关性，建立Copula融合的性能退化参数剩余寿命预测模型。

2）在唇形密封圈的性能参数的选取中，还可以考虑其他参数，如接触温度、接触宽度、油膜厚度等。实现多元数据融合的退化参数寿命预测模型。