知错善改,于错误中觉醒
2021-11-18 07:34:32霍燕
初中生世界 2021年42期
文/霍燕
勾股定理完美地诠释了直角三角形三边的数量关系,我们也可以用它来判定一个三角形为直角三角形,但有些同学在运用的过程中却频繁出错。下面列出几道易错题,旨在和同学们一起正视错误、寻找错因,从错误中反思、觉醒,以达到知错善改的目的。
易错类型一:缺说明过程
1.已知,如图1,在四边形ABCD中,AB=3,AD=4,BC=13,CD=12,∠A=90°,求四边形ABCD的面积。
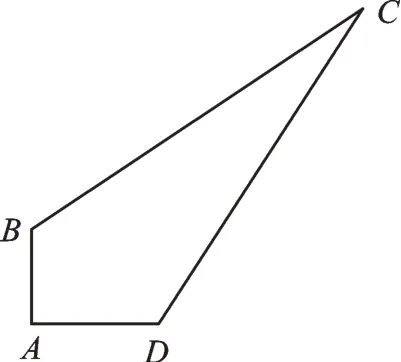
图1
【考点】勾股定理及逆定理的简单运用。
【错解】未证明△BCD是直角三角形。
易错类型二:考虑不周
2.已知直角三角形的两边分别是5和12,求第三条边的长。
【考点】三角形的三边关系、勾股定理。
【错解】答案不全。
易错类型三:图画不全或不会画
3.已知在△ABC中,AB=13,AC=20,边BC上的高为12,求△ABC的面积。
4.在平静的湖面上,有一只红莲,高出水面1米,一阵风吹来,红莲被吹到一边,花朵齐及水面。已知红莲移动的水平距离为2米,求水深。
【考点】勾股定理的应用。
【错解】第3题,图形画得出,但是画不全;第4题,画不出图。
参考答案:1.36。2.13或如图2,S=126;如图3,S=66。4.1.5米,图略。
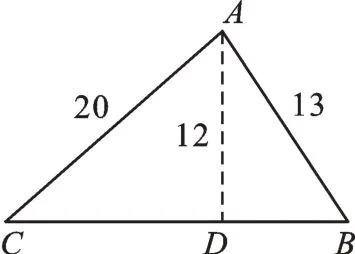
图2
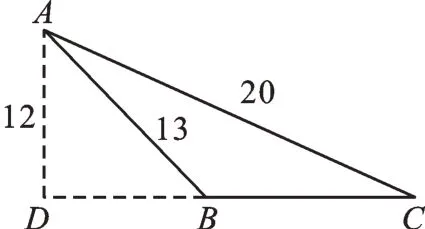
图3
猜你喜欢
中学生数理化·七年级数学人教版(2022年6期)2022-06-05 06:50:58
锦绣·上旬刊(2022年2期)2022-05-16 04:26:21
中学生数理化·八年级物理人教版(2022年4期)2022-04-26 14:11:16
河北理科教学研究(2021年2期)2021-08-18 08:34:00
中等数学(2021年1期)2021-07-23 01:41:00
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08 01:28:48
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:32
音乐天地(音乐创作版)(2019年10期)2020-01-06 11:51:54
黄河黄土黄种人(2019年7期)2019-12-20 03:06:34
音乐天地(音乐创作版)(2016年1期)2016-04-03 09:13:06

