大跨度PK断面斜拉桥静力分析

李云逸

摘 要：本文以在役桥梁武汉西四环汉江特大桥为工程背景，结合斜拉桥结构特点，利用大型通用三维FEA软件ANSYS建立全桥模型;在考虑大跨度斜拉桥几何非线性问题的条件下，模拟该桥成桥运营阶段的受力情况，得到静力分析主梁位移图、弯矩图和应力图，由此确定静载控制截面，为后续深度研究提供计算依据;最后根据分析得到的计算误差，分析误差产生原因，提出索力迭代计算方法。

关键词：大跨度斜拉桥;几何非线性;ANSYS;索力初张拉力

中图分类号：U441文献标识码：A文章编号：1003-5168（2021）17-0073-04

Static Analysis of Long-Span Cable-Stayed Bridge with PK Section

LI Yunyi

（School of Civil Engineering， Changsha University of Science & Technology，Changsha Hunan 410114）

Abstract： In this paper， taking the Wuhan West Fourth Ring Hanjiang Bridge in service as the engineering background， combined with the structural characteristics of the cable-stayed bridge， the full-bridge model is established by the large-scale general three-dimensional FEA software ANSYS; under the condition of considering the geometric nonlinearity of the long-span cable-stayed bridge， the stress condition of the bridge during the operation stage of the bridge is simulated， and the static analysis of the main girder displacement diagram， bending moment diagram and stress diagram are obtained， thereby determining the static load control section， so as to provide calculation basis for follow-up in-depth research; finally， according to the calculation error obtained by the analysis， the reason of the error is analyzed， and the iterative calculation method of cable force is proposed.

Keywords： long-span cable-stayed bridge;geometric nonlinearity;ANSYS;initial tension of cable force

斜拉橋是由拉索将主梁悬吊在塔柱上的组合受力体系桥梁。主梁受弯压，再通过斜拉索受拉传至塔柱，以此承担作用在主梁上的恒载及活载[1-3]。随着使用年限的增长，在役桥梁结构内外部会出现不同程度的损伤，要对其进行检测与评定。其间可通过有限元仿真模拟的方法来模拟桥梁受力情况，从而辅助判断桥梁病害形成原因[4-6]。本文以武汉西四环汉江特大桥为研究对象，利用ANSYS软件建立全桥模型，考虑非线性因素对其进行受力情况分析，为同类型桥梁计算提供参考。

1 工程概况

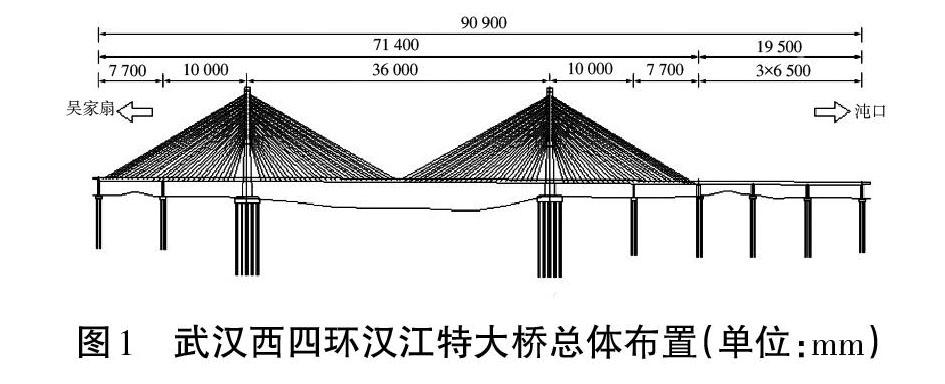
武汉西四环汉江特大桥主桥跨径布置（见图1）为77 m+100 m+360 m+100 m+77 m，桥长为714 m，桥宽为44 m，其为宽幅双塔双索面半漂浮体系预应力混凝土斜拉桥。主梁结构（见图2）为双边箱Π型PK断面预应力混凝土梁，箱梁顶板横向宽为43.6 m，每侧箱底宽为6 m，桥面板双向横坡坡度为2.5%。主梁混凝土等级为C55。拉索呈扇形布置，每个索面布置28对平行钢绞线斜拉索，全桥共设4对（224根）拉索。除过渡墩处梁上索距为4 m，其余位置均为6 m。索塔为H型，塔身采用矩形空心截面，上塔柱采用等截面，截面尺寸为7 m×5 m;中、下塔柱尺寸由7 m×5 m变化到12 m×7 m;索塔系横梁采用矩形空心结构，长为37 m，高为6 m，截面尺寸为6.6 m×6.0 m。索塔混凝土等级为C50[7]。

2 斜拉桥有限元分析理论

2.1 模型选择

大跨度斜拉桥拉索锚固点通常不会通过主梁扭转形心，桥梁受到多个方向荷载同时作用，采用平面分析显然不够，需要进行有限元空间结构分析，对结构进行空间静力离散：主梁简化为“鱼刺梁”模型，斜拉索简化为空间杆单元，桥塔简化为空间梁单元，拉索和主梁之间使用主从节点。

本文采用脊骨梁模型对桥梁进行模拟，主梁用一根通过主梁截面扭转中心的“鱼刺骨”模拟，拉索和横梁节点间采用刚臂连接，桥面系刚度和质量集中到中间节点上，以满足计算精度的要求。

2.2 几何非线性

斜拉桥的几何非线性主要表现在三个方面[5]。

2.2.1 垂度效应。垂度效应是斜拉桥在自重作用下产生下挠的现象，拉索越长，其自重作用越明显。在建立斜拉桥空间杆系模型时，通常使用杆单元模拟拉索，计算模型与实际结构的误差。多方考虑，在进行大跨度斜拉桥静力计算时，垂度效应不可忽略。

通常，计算采用等效弹模法，考虑拉索在重力作用下的垂度影响，其方法是用Ernst公式对拉索弹模进行修正，修正公式有二，计算时可以任选其一。

式中：[Eeq]为拉索的等效弹性模量，Pa;[Ee]为拉索弹性模量，Pa;[γ]为拉索换算容重，N/m3;[Lx]为拉索水平方向长度，m;[σ]为拉索应力，Pa;[ω]为拉索单位长度质量，kg/m;[T]为拉索拉力，N。

对于中小跨径斜拉桥，采用Ernst公式进行修正，精度足够，但大跨度斜拉桥自重和活载较大，仅用Ernst公式进行修正，精度不足。ANSYS模型中，link180单元具有大变形的特点，施加索力时需要考虑应力刚化效应，并通过索力迭代计算获得成桥索力，以消除垂度效应的影响。

2.2.2 梁柱效应。拉索拉力使主梁、主塔在运营阶段承受巨大应力而始终处于压弯状态，变形过程中，弯矩和轴力相互影响，形成梁柱效应。其静力分析方法为将轴力作为参数计入杆单元刚度矩阵中，并引入稳定函数对刚度矩阵进行修正。

2.2.3 大位移效应。荷载作用下，结构产生形变，导致荷载作用位置与方向发生明显变化，将产生与荷载增量不成线性关系的附加应力，进而影响结构切线刚度矩阵。因此，结构切线刚度由恒量变为以结构几何参数为自变量的函数，平衡方程也由线性关系变为非线性关系。求解采用拉格朗日法单元平衡方程，在ANSYS建模中通过大变形效应开关来实现。

3 计算模型

利用ANSYS软件建立全桥有限元模型，需要同时满足精确模拟和计算简便的要求。模型可以对桥梁结构进行适当簡化，达到近似模拟的目的。下面重点分析本次建模的要素。

3.1 单元选择

主梁、主塔及鱼刺单元采用beam188。拉索单元采用link180（2020版本软件可采用cable280，旧版本link10单元在help文件中不可查，命令流仍可调用），应设置为单向受拉。桥面轴线集中质量单元采用mass21。自定义截面辅助单元采用plane82。阻尼器及弹簧单元采用mass21+combin14。

3.2 主要参数

3.2.1 材料属性。除拉索外，该桥梁各部分材料参数如表1所示。拉索建模主要参数有索力、面积、等效弹性模量，全桥4个索面共有224根拉索，其对应参数从外部文件输入，方便后期调试修改。拉索弹性模量为195 000 MPa，考虑几何非线性影响，等效弹性模量[Eeq]采用Ernst公式加以修正。4种拉索材料参数如表2所示。

3.2.2 截面特性。主塔、主梁截面特性如表3所示。主塔下部设置变截面。

3.2.3 荷载参数。主梁混凝土容重按27.0 kN/m3计算，桥面铺装沥青混凝土，容重按24 kN/m3计，每侧的防撞护栏按10 kN/m计，二期线荷载共计70 kN/m。

3.3 分析要点

建模主要过程如下：一是建立坐标;二是定义单元;三是定义材料;四是定义截面;五是导入几何模型;六是划分网格;七是施加集中质量;八是约束与耦合。

建模过程中，人们需要注意以下几点：定义刚臂单元时，要定义材料刚度无限大，本文取梁单元弹性模量的100亿倍，且刚臂的密度设置为0;拉索单元有初应变，但link180单元无初应变输入，可在求解层采用降温法或inistate单位施加预应力;自定义截面网格尺寸不要过细，否则计算时间将大大增加;几何模型导入后，应进行布尔运算，同时打开主梁、主塔几何线的方向，检查同类构件的几何线方向是否一致;对于质量的处理，本文采用质量单元mass21，将质量等效到主梁节点上，分别算出三个方向的质量惯性矩;成桥状态计算完毕，要复核拉索轴力与初始输入索力是否一致，静力计算时打开应力刚化效应。

3.4 边界条件与约束

主塔、主梁固结。主梁、桥墩平动自由度耦合为横向约束（[x]方向）和竖向约束（[z]方向）。桥梁为半漂浮体系，主塔、主梁处也需要耦合。墩和塔底全部进行固接处理。

3.5 全桥有限元分析模型

主梁、主塔截面利用ANSYS软件自定义截面功能。主梁截面由CAD软件导入，主塔截面划分为两段，上半段为等截面，高度为66.9 m;下半段高度为65.2 m，采用参数化编程建面、划分网格，最后定义变截面。拉索参数由外部文件输入，在solu层输入初应力。全桥共有771个节点和1 105个单元，有限元模型如图3所示。

4 成桥状态与车道荷载计算

4.1 成桥状态计算结果

斜拉桥结构荷载组合包括恒载和活载。恒载包括一期恒载（桥梁自重）、主梁二期恒载（桥面铺装、防撞护栏、标注标牌等）;活载包括汽车荷载、人群荷载等。本文通过计算得到全桥恒载作用下的位移及受力情况，如图4至图7所示。

由图4至图7可知，武汉西四环汉江特大桥主梁跨中挠度最大，主梁最大竖向位移为209 mm，挠度最小值出现在桥塔位置。主梁弯矩与连续梁相似，主梁最大弯矩值为正弯矩，出现在桥塔处。结合现场检测情况，模型计算所得受力和变形趋势基本与实际情况一致，可取跨中和桥塔位置做控制截面，后续研究中设置不同工况对其进行进一步研究。

4.2 成桥索力调整

由图6可知，计算索力与成桥测得实际索力之间仍然存在误差，它是由拉索垂度效应导致的模型与实际结构间的误差。下面进行分析并提出索力求解方法。ANSYS软件以后不再推荐Link10单元，拉索常用Link180单元模拟。Link180单元预应力的模拟可采用初应变法或降温法来实现。因此，人们可以通过将索力换算成初应力的方法，施加拉索出张拉力。

在结构未变形情况下，人们可以直接施加成桥恒载作用下的索力，即设计索力。然而，实际张拉过程中，恒载作用导致结构变形，拉索索力必然发生改变。这便是本文计算的主要误差来源。因此，计算分析时需要对索力进行反复求解和调试，找到一组初始索力，使计算所得的拉索轴力与拉索初张拉力相一致。

计算步骤如下：一是令成桥索力[F]为初始索力[F0]，并将该索力[F0]换算为初应力施加到拉索单元上;二是考虑几何非线性影响，进入静力分析求解层后打开大变形效应，利用牛顿-拉普森法改变[F0]数值，求出索力[F1];三是进行索力迭代，用DO循环，每求解一次，提取索力，检查索力与输入的初张拉力误差是否小于允许值，若小于允许值，则输出结果，否则使[F0=F-F1]，重复上述步骤，直至计算的索力误差满足条件;四是输出[F0]。迭代后索力误差如图8至图11所示。

5 结语

大跨度斜拉桥静力计算中，非线性因素对结构计算的影响较大，不可忽略。本文利用有限元分析软件ANSYS建立空间杆系模型，计算得到其静力学受力和变形情况。由结果可知，对于该类大跨度宽幅斜拉桥，仅用Ernst公式修正弹性模量的办法，不足以消除垂度效应对计算精度的影响，需要考虑初张拉。本文提出成桥索力的调整方法，以实现成桥时索力状态的精确模拟。

参考文献：

[1]刘士林，梁智涛，侯金龙，等.斜拉桥[M].北京：人民交通出版社，2004：89.

[2]叶裕明，刘春山，沈火明，等.ANSYS土木工程应用实例[M].北京：中国水利水电出版社，2007：67-68.

[3]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007：28.

[4]交通运输部.公路桥梁荷载试验规程：JTG/T J21-01—2015[S].北京：人民交通出版社，2016.

[5]沈伟，王利刚，方振.几何非线性对大跨径斜拉桥荷载试验计算结果影响[J].智能城市，2021（1）：132-133.

[6]柯亮亮，姚强，冯威，等.独塔斜拉桥荷载试验有限元分析与评价[J].城市道桥与防洪，2016（8）：117-120.

[7]舒江，师少辉，朱玉，等，武汉西四环汉江特大桥总体设计[J].桥梁建设，2017（6）：84-88.