基于主成分分析及GA-LM的水产养殖环境溶解氧和氨氮含量预测
姚启,缪新颖, 2*
(1.大连海洋大学 信息工程学院,辽宁 大连 116023; 2.辽宁省海洋信息技术重点实验室,辽宁 大连116023)
水产养殖是一个包括多参数的复杂过程[1]。其中,溶解氧(dissolved oxygen,DO)和氨氮含量是决定水产养殖产量的重要因素[2-3],DO过高或过低都会导致养殖生物死亡[4],氨氮直接反映养殖水质的污染程度,过高直接影响养殖生物的生存状态。因此,在水产养殖环境中对二者进行预测,对水产养殖业具有重要的意义。
DO和氨氮含量的预测均为非线性问题[5],二者受多种因素影响,且各因素之间存在复杂的耦合关系[6],因此,难以利用统计的方法建立准确的预测模型,故而以神经网络和支持向量机(support vector machine,SVM)为代表的非线性问题解决工具,被研究者应用于DO和氨氮预测[7-11]。但是,SVM和误差反向传播神经网络(back propagation neural network,BPNN)具有极大的局限性[7-8],易引入冗余数据,且针对复杂问题的泛化能力受到一定的制约[12]。神经网络的结构很多都是通过试凑法来实现[4,13],导致运行费时。另外,DO和氨氮影响因素复杂,且相互之间存在很大的耦合性,很难确定神经网络的最佳输入,若将相关的影响因素全部直接引用,不仅会引入大量冗余数据,而且会由于多重共线性降低网络的训练速度和效率,影响预测精度[14]。
Levenberg-Marquardt(LM)神经网络算法利用高斯-牛顿法可以在最优值附近产生一个理想的搜索方向,从而保持较快下降速度的特点,使网络能够有效收敛,可以大大提高网络的收敛速度和泛化能力[5]。遗传算法(genetic algorithm,GA)是一种模拟自然进化、搜索最优解的方法,适合用来优化神经网络的结构[5]。主成分分析(principal component analysis,PCA)方法一方面可以通过提取正交的各主成分,有效避免多重共线性,提高参数估计的准确性;另一方面可以对包含较多变量的影响因子数据集进行降维,使尽可能少的变量包含尽可能多的信息,从而使模型所包含的信息更丰富,建模更有效[15]。
基于以上考虑,本研究中构建了一个综合GA、LM和PCA算法优点的GA-LM-PCA水产养殖环境DO和氨氮含量预测模型,利用PCA算法确定DO和氨氮含量预测模型的有效影响因子,利用LM算法训练神经网络,利用GA优化神经网络结构,以期为水产养殖重要环境因子的预测提供有效工具。
1 基于GA-LM-PCA的预测模型
1.1 水产养殖环境DO和氨氮的影响因素分析
影响水产养殖环境DO含量的因素复杂,主要包括水体温度、水体含氮量和空气中氧气组分的分压力等[7-8],其中一些因素在一定条件下对某一具体养殖环境和测量点可以认为是不变的[5]。影响水产养殖环境氨氮含量的因素主要有水温、pH、DO和电导率等,其中水温、pH越高,氨氮的毒性就越大,DO也直接关系到氨氮、亚硝酸氮和硝酸氮之间的转化效果,电导率能体现养殖环境中离子的量[9]。
本研究中,水产养殖水样采集自大连獐子岛股份有限公司养殖基地。综合考虑各变量的可测性,选取水温、盐度、叶绿素a、电导率、浊度、风速、亚硝酸盐、氨氮和总氮9个变量作为DO的影响因素;初步选取水温、pH、DO和电导率4个变量作为氨氮的主要影响因素,在考虑多因素分析时,选取水温、盐度、叶绿素a、电导率、浊度、风速、亚硝酸盐、DO、pH和总氮10个变量作为氨氮的影响因素。采用浮标在线监测水温、盐度、叶绿素a、电导率、浊度、风速,采用多参数水质监测仪(YSI600XLM,美国)现场测定亚硝酸盐、pH、氨氮和DO含量,采用全自动总氮分析仪测定总氮含量(IL500,美国HACH公司)。
1.2 水产养殖环境DO和氨氮含量预测模型GA-LM-PCA的建立
从大连獐子岛股份有限公司2011—2012年所收集的监测数据中选取其中的1 200组作为建模数据,其中,1 100组作为训练样本,100组作为测试样本。用PCA确定养殖环境DO和氨氮有效影响因子的基础上,采用GA-LM方法进行预测。预测流程图如图1所示。

图1 基于GA-LM-PCA模型的水产养殖环境DO和氨氮含量预测流程图
1.2.1 基于PCA算法的水产养殖环境DO和氨氮有效影响因子的确定 考虑到水产养殖环境DO和氨氮含量影响因素众多,且相互之间存在着多重共线性,利用主成分分析方法确定DO和氨氮含量的有效影响因子,从而达到去耦合降维的效果。具体步骤如下:
1)对水产养殖环境DO和氨氮的影响因素进行标准归一化,以消除不同影响因子数值的平均值和方差大小对变量比较产生的影响。计算公式为
其中:xi为每个样本的第i个影响因素;xi mean为影响因素的平均值;σ(xi)为影响因素的标准差。
2)求样本协方差矩阵,即
i=1,2,…n;j=1,2,…,p。
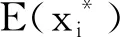
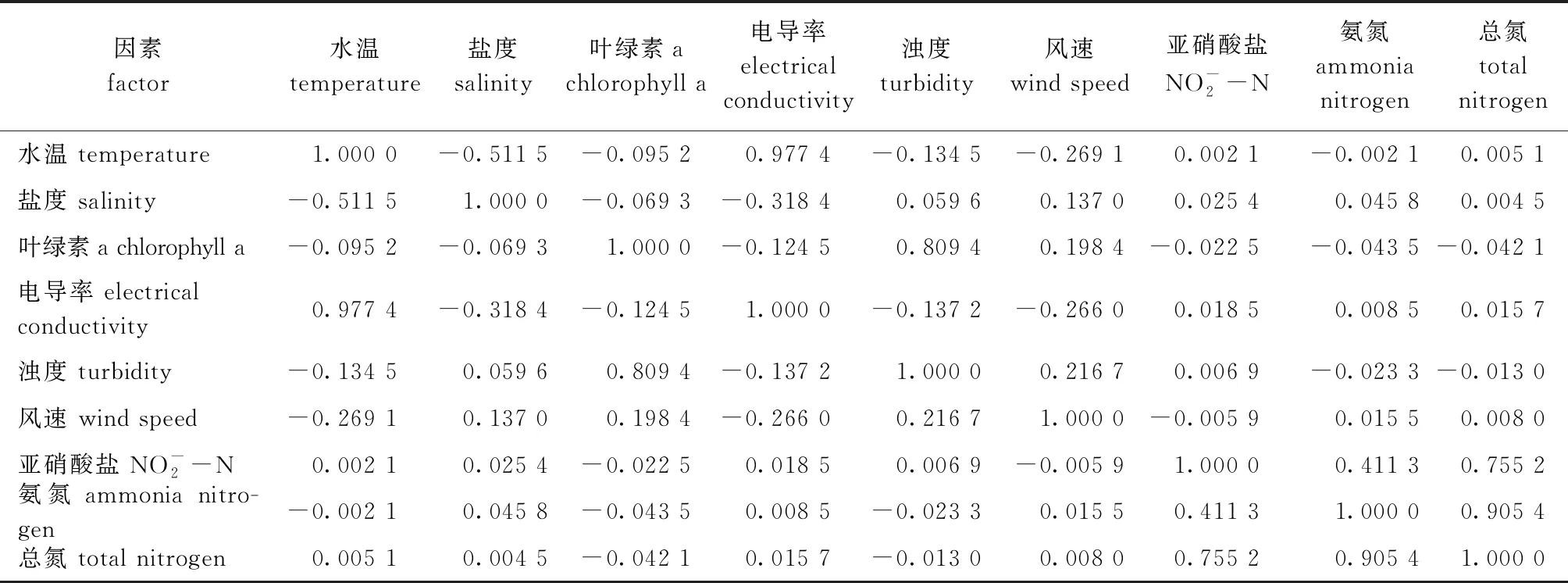
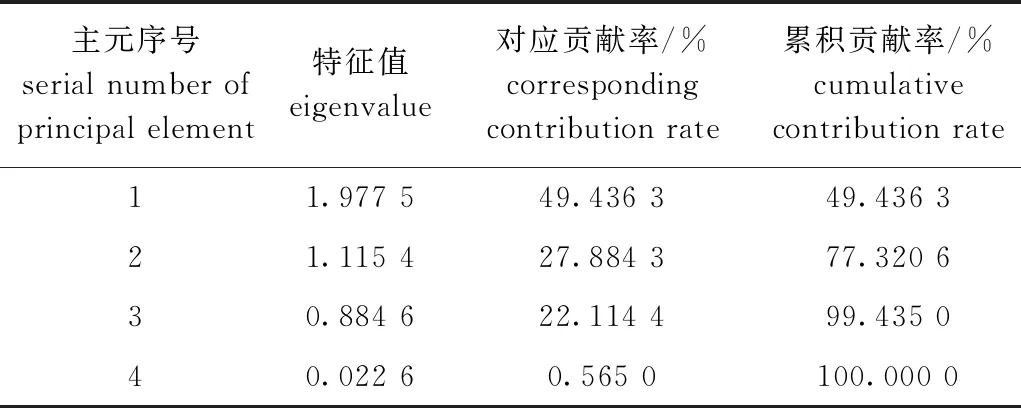
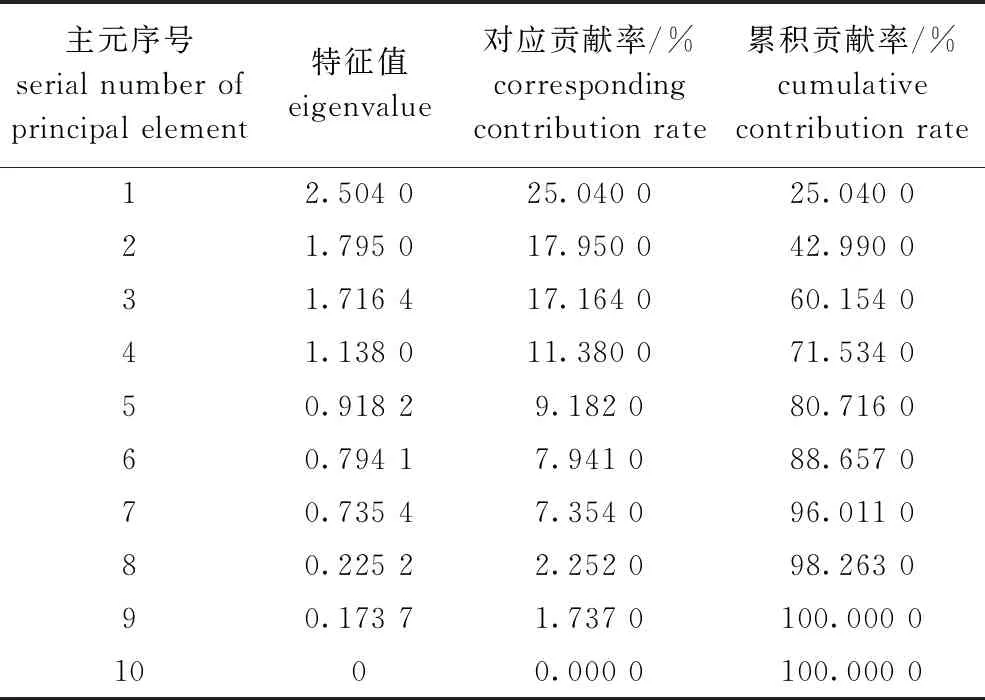
4)对λi按照降序排列,计算出所有主元的累积贡献率,并将累积贡献率大于85%的前m(m 5)计算前m个主元对应的特征向量μi,构建其变换矩阵D,即 D=(μ1,μ2,…,μm)T。 (4) 6)求出前m个主成分表达式,并将其作为GA-LM输入,主成分Z计算公式为 Z=DX*。 (5) 1.2.2 基于GA的水产养殖环境DO和氨氮含量预测模型结构的确定 本研究中采用典型的3层神经网络,隐层节点数、最优权值和阈值等网络结构因素均由GA来完成。主要步骤如下: 1)初始化种群并编码。用染色体表示神经网络结构,在编码时具体包括结构基因与权重基因。结构基因采用二进制编码,表示隐层节点结构(“1”表示存在隐层节点,“0”表示不存在);连接权值和阈值用权重基因wn(x+y)表示,利用实数进行编码。当有n个隐层节点、x个输入、y个输出时,染色体编码的结构如图2所示。 图2 染色体编码结构 本研究中种群初始值设为100,初始隐层节点设为30。 2)适应度评价,计算公式为 E=∑(S-V)2,F=1/E。 (6) 其中:V是经LM训练神经网络得到的预测值;S是所对应的实际测量值;E是误差平方和(SSE);F是适应度函数。总体向适应度函数F高的方向进化, 误差逐步减小,结构逐步趋于简单。 3)确定终止进化条件。本研究中确定了两个进化终止依据,二者为“或”的逻辑关系。具体为迭代次数达到500,或均方差(MSE)小于0.000 1。 4)遗传算子。具体包括选择、交叉和变异算子,本研究中采用不同的策略[5]。选择算子采用了轮盘赌策略;交叉和变异算子则根据染色体编码结构采用了不同的策略,其中结构基因采用单点交叉和基本位变异算子;权重基因采用算术交叉和非均匀变异算子。初始交叉率和变异率分别设置为0.6和0.08,可以自适应调整,调整公式为 其中:Fmax为种群的最大适应度值;Favg为种群的平均适应度值;F为要交叉的两个个体中较大的适应度值;F′为要变异个体的适应度值;k1、k2、k3、k4为常数。 1.2.3 基于LM神经网络的水产养殖环境DO和氨氮含量预测算法 LM算法是在BPNN算法基础上的一种修正算法,能够克服BP算法容易陷入局部极小、收敛速度慢、泛化能力弱等不足。在修正过程中,权值的调整算法公式为 ΔW=-[JT(w)J(w)+αI]-1·JT(w)e(w)。 (8) 其中:J(ω)为Jacobian矩阵;α为大于零的调整因子,用于控制LM算法的迭代;I为单位矩阵。本研究中α的初始值设为0.01。 对1 100组DO样本归一化后的部分水产养殖环境数据见表1,归一化后的样本数据变化范围变小,可以消除不同影响因子数值的平均值和方差大小对变量比较产生的影响。 表1 归一化后DO含量的影响因素 对应的水产养殖环境DO样本的协方差见表2,DO的9个影响因素之间具有一定的耦合性,需要去耦。利用GA-LM-PCA模型对DO含量进行预测,得到如表3所示的DO降序特征值和贡献率。 表2 水产养殖环境DO样本的协方差 从表3可见,前5个主元的累计贡献率大于85%,且特征值较大,因此,选取主成分数目为5个。 表3 DO的降序特征值和贡献率 按照式(4)和(5)求出的主成分表达式为 在此基础上,得到如图3、4所示的5-10-1水产养殖环境DO含量预测网络结构和预测结果。 图3 5-10-1水产养殖环境DO含量预测网络 将文献[9]中所采用的水温、pH、DO和电导率4个变量作为影响因素,依然采用1 200组监测数据作为样本,其中1 100组作为训练样本,100组作为测试样本,同样利用GA-LM-PCA模型对氨氮含量进行预测,得到如表4所示的降序特征值和贡献率。从表4可见,前3个主元的累计贡献率大于85%,且特征值较大,因此,选取主成分数为3。在此基础上,可以得到3-8-1的氨氮含量预测网络结构(图略)和预测结果(图5)。 表4 氨氮的降序特征值和贡献率 2.3.1 DO含量预测比较 为了验证GA-LM-PCA的预测效果,将GA-LM-PCA 的预测结果与直接引用影响因素的GA-LM模型进行比较。采用直接引用变量法,将水温、盐度、叶绿素a、电导率、浊度、风速、亚硝酸盐、氨氮和总氮9个变量作为DO的影响因子,采用GA-LM模型对DO含量进行预测,结果如图6所示。 将图6与图4的DO含量预测结果进行比较,可以看出,GA-LM-PCA模型预测结果明显优于未用PCA方法的GA-LM 模型,二者具体性能比较如表5所示。从表5可见,利用GA-LM-PCA预测DO含量,尽管PCA确定有效影响因子需要花费一定的时间,但能够有效地对影响因素解耦降维,运行耗时反而降低,平均绝对误差与均方根误差也均小于GA-LM模型法,提高了预测精度。 图4 DO含量的GA-LM-PCA模型预测结果 表5 GA-LM-PCA与GA-LM模型预测DO含量的效果比较 图6 DO含量的GA-LM模型预测结果 2.3.2 氨氮含量预测比较 将水温、pH、DO和电导率4个变量作为影响因素对氨氮含量进行预测,采用不加PCA的GA-LM模型预测结果如图7所示。 将图7与图5的氨氮含量预测结果进行比较,可以看出,GA-LM-PCA模型预测结果稍好于未用PCA方法的GA-LM 模型,二者具体性能比较如表6所示。从表6可见,两种模型的输入量个数相当,而GA-LM模型输入量本身就是行业内所认为相关度最高的4个量,所以未用PCA和使用PCA法所确定的GA-LM模型预测的平均绝对误差和均方根误差都非常接近,而且在输入量非常接近的情况下,未用PCA方法的运行反而耗时更短。 表6 GA-LM-PCA与GA-LM模型预测氨氮含量的效果比较 图7 氨氮含量的GA-LM模型预测结果 对于同期监测的1 200组样本,将氨氮的影响因素从之前的4个增加到10个,具体为水温、盐度、叶绿素a、电导率、浊度、风速、亚硝酸盐、DO、pH和总氮,利用同样的GA-LM-PCA方法对其预测,得到表7所示的降序特征值和贡献率。从表7可见,前6个主元的累计贡献率大于85%,且特征值较大,因此,选取主成分数目为6。在此基础上,得到6-18-1的氨氮含量预测网络结构(图略)和预测结果(图8)。 表7 增加影响因素数量后氨氮的降序特征值和贡献率 将图8与图5 的氨氮含量预测结果进行比较,可以看出,含有10个影响因素的GA-LM-PCA模型的预测结果明显好于含有4个影响因素的GA-LM-PCA 模型,二者具体性能比较如表8所示。 图8 增加影响因素数量后氨氮含量的GA-LM-PCA模型预测结果 从表8可见,将影响因素增加到10个后,影响因素尽可能地被考虑进来,此时采用GA-LM-PCA模型的氨氮含量预测效果明显提高。可见,采用GA-LM-PCA模型不用考虑由于引入大量低相关度甚至无关影响因素对预测效果产生的负面影响,对于有效影响因子难以确定的场合,适当增加影响因素选取范围,就可以取得较好的预测效果。 表8 不同影响因素数量下氨氮含量的GA-LM-PCA预测模型性能比较 在水产养殖环境DO与氨氮含量的预测模型中,二者的预测受各因素之间存在复杂的耦合关系的影响,很难确定神经网络的最佳输入,冗余影响因素会降低训练速度和效率,影响预测精度。本研究中,采用GA-LM-PCA模型对水产养殖环境中的DO和氨氮含量进行预测,即采用PCA确定影响因素,用LM训练神经网络。付泰然[16]提出采用SAE-BP神经网络预测水体氨氮,得到氨氮含量预测结果的均方根误差为0.140 5,而本研究中GA-LM-PCA模型对氨氮含量预测结果的均方根误差为0.011 1,预测精度同样呈倍数提升。曹首启等[17]提出在传统遗传算法神经网络优化模型的基础上寻找最优误差输出及遗传算法优化的BP神经网络预测模型,对DO含量预测结果的平均误差由0.077 8 mg/L下降至0.0177 mg/L,精度提高了3.4倍,而本研究中GA-LM-PCA预测模型相较于此模型的DO含量预测的精确度提高了27.8%。由此可见,GA-LM-PCA预测模型在同类预测模型应用中处于预测精度较高的水平。 本研究中使用PCA方法的GA-LM模型可以有效避免多重共线性,提高参数估计的准确性,用GA-LM-PCA预测的氨氮值平均绝对误差较未用PCA方法的GA-LM模型提升了12.7%,而DO值则提升更多,同时大量低相关度影响因素对GA-LM-PCA预测模型的负面影响较小,可以通过增加影响因素的范围来提升预测精度,应用性较好,本研究结果为水产养殖生产过程中的DO与氨氮参数预测提供了新的方法。 1)本研究中提出的PCA-GA-LM模型预测的DO和氨氮值与实测值吻合度均高于直接引用变量法的GA-LM模型,平均绝对误差和均方根误差也均小于直接引用变量法,提高了预测精度,可以作为水产养殖重要环境因子预测的一种有效工具。 2)PCA-GA-LM模型对于同样数量的样本,选取的影响因素越多预测效果越好,这意味着本模型对于相关度低、冗余的影响因素具有自动筛选功能,能使其中相关的影响因素充分发挥作用,且能去掉影响因素之间的耦合,能够为机理复杂、影响因素难以确定的非线性系统提供可行的预测方案。
2 养殖环境中DO和氨氮含量的预测
2.1 DO含量的预测结果




2.2 氨氮含量的预测
2.3 利用PCA和未用PCA的GA-LM模型预测结果比较





2.4 影响因素的数量对GA-LM-PCA预测模型的影响


3 讨论
4 结论

