高灵敏度感应式磁传感器测量误差校正算法

张士荣，郭 强

(1. 江苏理工学院，江苏 常州 213001；2. 南京理工大学，江苏 南京 210094)

1 引言

电磁波探测技术是一种发展成熟的地质勘测方式，现阶段，相关企业与研究人员开发出一系列相关产品，例如大地电磁测深仪、瞬变电磁仪等[1]。低频电磁波能应用在地质测量、地壳通信、磁场勘测和地球物理观测等领域。传统勘测通常运用铺设线圈方法接收信号，但因受到地理空间约束，铺设大量线圈给测量工作带来极大不便[2-3]。高灵敏度感应式磁传感器能有效解决上述问题，在缩短体积的同时完成相等甚至更高的精准度，在电磁波应用中拥有举足轻重的地位。

考虑到不同环境下由于工艺及安全水准等原因，高灵敏度感应式磁传感器有时会产生偏移误差。徐祥[4]等人提出基于自适应参数估计的磁传感器实时校正算法，对参数进行实时估计和处理，构建基于模值的参数估计方程，分析参数模型噪声特性，针对非高斯状态相关噪声提出采用自适应参数估计方法，完成磁传感器误差的校正。但该算法对测量误差因素考虑较少，难以保证校正结果的可靠性；王鹏飞[5]等人设计了基于误差分离的矢量校准算法，用于感应式磁传感器正交性校正。构建正交性校正矢量校准数学模型，对校正过程中的安装误差采取误差项分离校正，融合卡尔曼滤波与最小二乘法求解模型参数，获得正交性校正矩阵。但该算法的计算耗时较长，证明其实时性较差。

针对传统方法存在的不足，本文建立一种基于改进遗传算法的测量误差校正算法。首先详细分析高灵敏度感应式磁传感器工作机理和灵敏度影响元素，分类测量误差来源，创建磁传感器误差模型，运用自适应方法完善遗传算法内的交叉算子和变异算子，实现高精度测量误差校正目标。

2 高灵敏度感应式磁传感器灵敏度分析

在感应式磁传感器内起到关键作用的是线圈与磁芯，绕制的线圈用于感应穿过其内部磁通量的变化，从而生成感应电动势。通过引入高磁导率的磁芯，能把信号增强若干倍。磁传感器外磁场发生改变时，线圈轴线和磁场平行方向获得的感应电压为

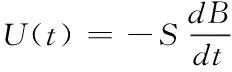
(1)

其中，S是绕制线圈的有效面积，B表示外磁场的磁感应强度，负号是感应电压方向。如果变化的外磁场是正弦信号，则存在

B=B0sinωt

(2)

设定后级放大器的放大倍数是A，线圈匝数是n，磁芯有效导磁率是μa，绕制线圈有效面积计算公式描述为

S=ns0μaA

(3)

磁传感器感应电动势绝对值为

|E|=|2πens0μaAB0cosωt|

(4)

通过式(4)可以看出，感应电压和信号频率e、线圈匝数n、骨架横截面积s0、导磁率μa成正比，测量误差校正可从这几个参数入手。

电磁波在大地电磁勘测中传播时，会有很多损耗，且低频干扰信号强[6]。针对低频弱信号，怎样增强灵敏度是传感器设计的重点。

倘若磁场信号是正弦波信号，传感器附带有增益是前置放大器，感应线圈灵敏度是线圈在单位磁感应强度改变中所呈现的感应电动势，则可将灵敏度运算公式描述成

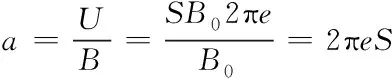
(5)

通过式(5)可知，在相同频率情况下，灵敏度和S成正比。因此，提高有效面积是增强灵敏度的可靠路径。针对骨架固定传感器，有效导磁率取决于磁芯材料与长径比，将有效导磁率记作

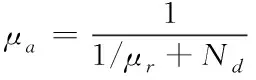
(6)

其中

(7)

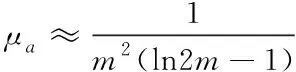
(8)

其中，μr表示相对磁导率，Nd是退磁因子，L是磁芯长度，d是磁芯直径。

3 测量误差模型构建

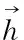
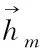
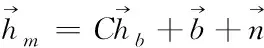
(9)

式中

C=CsCηCα

(10)

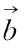
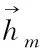
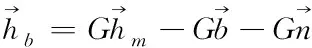
(11)

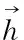
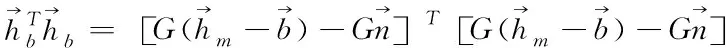
(12)

理论状况下，感应式磁传感器三个向量在不同状态下的值会在原点组成一个球心，半径是测量区域地磁场标量值的某个球面。

针对测量值大小，根据式(12)中可知，不同状态下的全部测量值都被收敛在一个椭球面内[8]。而硬铁误差划定了椭球中间方位，软铁误差与标度系数误差可以改变椭球长短轴及扁率，而椭球长轴指向则取决于装配弧度误差与软铁误差。

让Γ值满足下列约束：

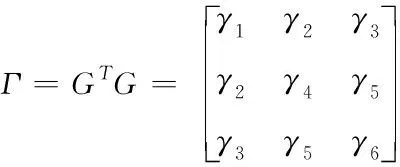
(13)

结合式(12)可得到N组测量方程的线性模式

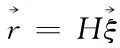
(14)

由于式(14)内H具有噪声，使用总体最小二乘法对ξ进行估计[9]，得到

(15)

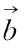
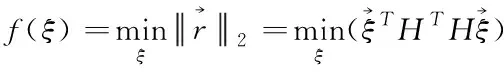
(16)

4 改进遗传算法下的测量误差校正

从高灵敏度感应式磁传感器原理分析中可知，需要优化的参数个数很多，很难寻找到最优值，需要引用全新的计算方式。因此，本文采用遗传算法实现参数最优处理。

遗传算法是一种拟照大自然生物演化过程的高随机性搜寻手段，目标函数无需连贯，计算简便，具备很强的鲁棒性，在组合优化、模式识别等领域得到充分运用[10]。融合感应式磁传感器校正参数求解，完成改进遗传算法设计，将其代入测量误差模型内，实现高精度测量目标。

设定一个误差函数f

f=min[max(|Bj|-|Bs|)]

(17)

其中，f为包含信号频率e、线圈匝数n、骨架横截面积s0、导磁率μa的函数，|Bs|为设定的外界标准磁场模值，|Bj|为感应式磁传感器在姿态j下测量修正值的模。

测量误差校正的目标是探寻式(17)中的最小值，在遗传算法内个体函数值越低适应度越高。把式(17)当作适应度函数，把e、n、s0和μa引入适应度函数，函数值越低，个体适应度越高，存活概率越高。

基于此，择优处理使用交叉、变异及选择等有关算子。选择算子是遗传算法的典型算子之一，该算子从上一代种群内剔除适应度小的个体，尽可能保留适应度高个体，组成若干能够繁衍后代的子群体，实现模拟自然界优胜劣汰机制目标。

交叉算子能有效获得新一代的个体形式，新个体具备父辈个体优良特征，可达到算法全局搜寻目标。但在实际操作中，若交叉概率过高，会破坏群体内的良好模式，倘若交叉概率值过低，新个体生成的速率会变得缓慢，因此要严格控制交叉算子取值。

在传统遗传算法计算过程中，交叉概率一般任意选择一个很高的值，而变异概率通常情况下会很低。交叉概率Pc取值范围在0.25～0.88之间，变异概率Pm取值范围是0.01～0.15，具有很强的盲目性。

在明确遗传算法内关于交叉算子与变异算子择取盲目性前提下，使用改进遗传算法完成误差校正任务[11]。运算根本思路为：利用自适应变化的交叉概率与变异概率替代原有概率，让两个概率伴随种群进化进行对应改变，完善后的方法能优化全局搜寻能力与收敛效率，同时在搜寻流程后期方法收敛稳定性依旧很好。

从种群内独立个体角度出发，交叉概率值高低应该和个体适应度值拥有密切关系；从种群全局进化流程角度，伴随进化流程不断深入，交叉概率要慢慢减少，直至最后变成一个平稳值，防止对算法后续稳定性造成不良影响，让整个算法无法收敛或收敛速度慢。从生成全新个体方面考虑，种群全部个体在交叉运作中要拥有相同地位，令遗传算法无论处于搜寻空间的每个方位均具备匀称性。

在真实操作中，如果要获得满足以上各个需求的交叉算子难度很高，创建仅和进化代数有关，和个体适应度无关联的交叉概率运算方法，具体计算过程为

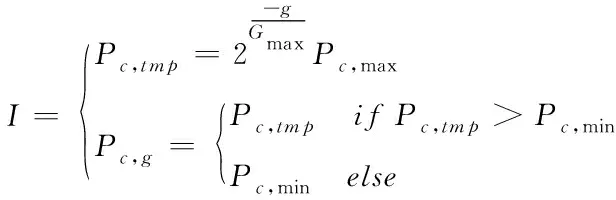
(18)

其中，Pc，tmp表示交叉概率中间参变量，Pc，max是设定的最大交叉概率，Pc，min是设定的最小交叉概率，Gmax代表最高进化代数，g是目前进化代数，0≤g≤Gmax，Pc，g是目前种群交叉概率。

比较理想的变异概率应当随着个体优劣不断改变，也就是劣质个体的变异概率变大[12]，为优良个体赋予较低的变异概率。本文使用式(19)推导个体适应度的自适应变异概率

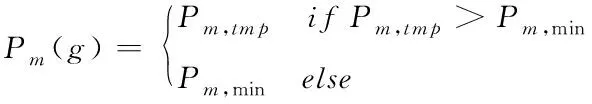
(19)

其中，Pm，tmp表示变异概率中间参变量，Pm，max是设定的最高变异概率，Pm，min是设定的最低变异概率，Fmax是个体的最佳适应度值，Fmean是个体适应度均值，F(μ)是等待变异适应度值，Pm(g)是现阶段种群个体变异概率。

最后把式(18)与式(19)分别代入式(17)中的误差函数，求解出准确的测量误差校正参数，提升高灵敏度感应式磁传感器的测量精度。

5 实验与分析

为验证上述高灵敏度感应式磁传感器测量误差校正算法的有效性，分别通过数值仿真和实测数据对感应式磁传感器测量误差校正算法的性能展开分析。其中，数值仿真用于明确算法参数估计的正确性，实测数据仿真用于证明算法真实有效性。

考虑到随机测量噪声影响，对算法实施Monte Carlo仿真，表1为应用本文算法实施参数估计的平均结果。

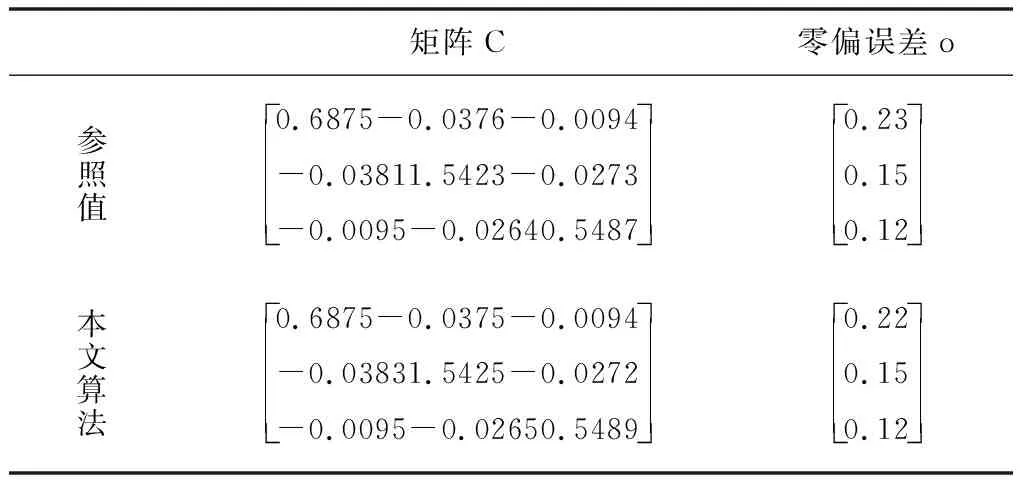
表1 模型参数设定

从表1中可知，本文算法可以准确估计出参数{C，o}，所得结果和参照值比较接近。

图1为校正前后的测量重力场模值。从图1中可知，在各种误差综合影响下，未校正数据展现出较大起伏的波动，而本文算法校正后的测量模值都处于参照重力场模值周边范围。其原因在于本文算法使用改进遗传算法，准确求解校正参数，有效增强所提方法整体校正精度。

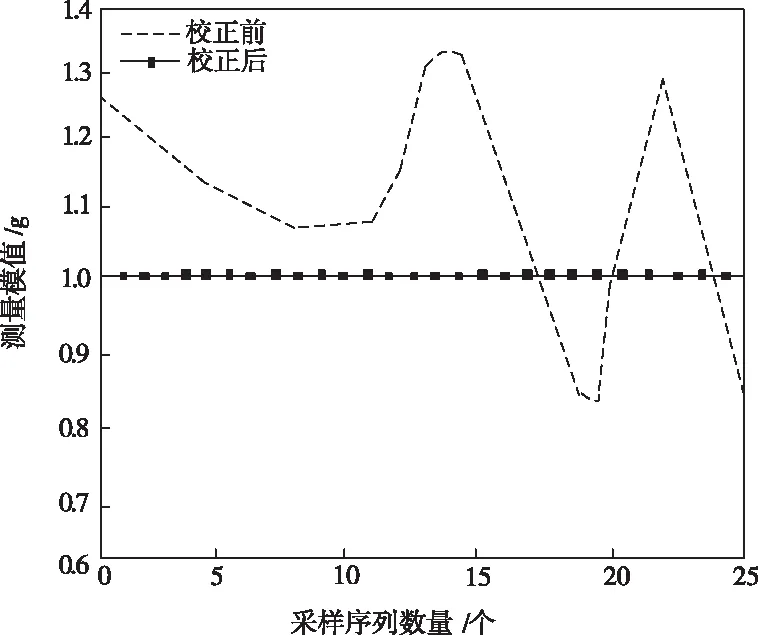
图1 校正前后重力场模值和参照模值仿真结果对比

为深入探究本文算法有效性，使用感应式数字加速度计进行实测验证。测量数据利用微控制器从传感器读取，采样频率是150Hz，微控制器利用串行接口协议把数据转发至上位机完成数据收集。把加速度计静置15s时间，并求出其测量均值，得到不同姿态状况下150组重力加速度测量数据。然后使用本文算法实施测量误差校正，校正结果如图2所示。

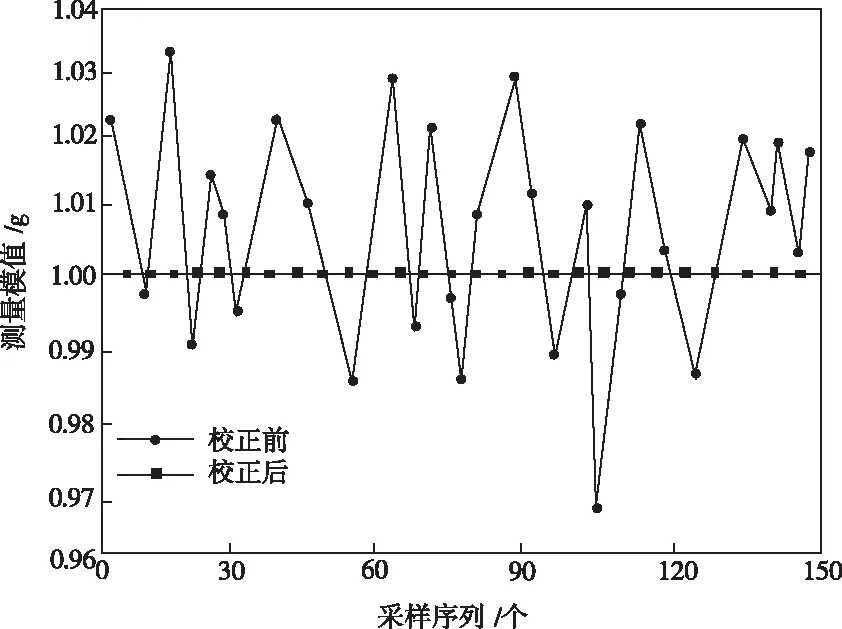
图2 校正前后重力场模值和参照模值实测结果对比

根据图2可以看出，校正前的加速度数据模值上下起伏比较剧烈，而本文算法校正后的加速度数据模值和参照重力场模值相差较小。证明应用本文算法后，获得的测量误差校正参数合理、有效。

6 结语

面向不同环境因素下导致的磁传感器测量误差问题，本研究提出一种基于改进遗传算法的测量误差校正算法。该算法具有优秀的校正精度、鲁棒性强、操作简便的优势，能够为大地电磁测深勘探领域提供更加可靠的数据资源。但在改进遗传算法步骤中，没有考虑选择算子染色体变化规律在校正求解中的应用，今后会对这一方面加以跟进。