结合协同机制与动态调控策略的双蚁群算法
孟静雯,游晓明+,刘 升
1.上海工程技术大学 电子电气学院,上海201620
2.上海工程技术大学 管理学院,上海201620
旅行商问题(traveling salesman problem,TSP)是指从任一个地方出发,遍历完所有的城市后,最终回到出发点,使所走的总路程最短。
20 世纪90 年代,意大利学者Dorigo 等人提出蚁群系统(ant system)[1],这是受蚂蚁觅食行为的启发提出的一种元启发式算法,随后引起了专家学者的重视,并运用于求解TSP。最初蚂蚁系统(ant system,AS)有三个不同的版本,分别称为蚂蚁数量(ant quantity)、蚂蚁密度(ant-density)、蚂蚁周期(antcycle)[2]。如今经常使用的是蚂蚁周期(ant-cycle)这个版本。随着测试规模的扩大,AS 算法在工作过程中存在需要较长搜索时间和易于陷入局部最优问题,随后Dorigo 等人在AS 算法的基础上进行了改进——使用精华策略的蚂蚁系统(elitist strategy for ant system,EAS)[2]。它的思想与AS 不同之处在于向全局最优路径添加额外的反馈信息。1996 年,Dorigo在AS的基础之上提出了蚁群系统(ant colony system,ACS)[3],加入全局信息素更新规则,并且采用了一种更积极的行为选择规则,使得ACS 在解决规模较大的TSP 问题时会得到更优解。然而ACS 算法在求解TSP问题时仍然存在收敛速度慢、多样性较差的问题。
针对上述问题,许多改进策略被提出。张涛等人[4]将蚂蚁划分为不同等级,采取等级反馈机制策略对不同等级的蚂蚁走过的路径进行不同程度的正或负反馈,加快算法收敛速度。王昕宇等人[5]利用全局记忆矩阵指导负载蚂蚁向最相似的数据对象方向前进,避免蚂蚁漫无目的移动,保证了算法较快收敛。这些改良方案虽然提高了收敛性,但是没有提高解的质量。针对这一缺点,张玉茹等人[6]在进行路径构建时,引入贪心算法平衡信息素浓度与启发式信息两者对蚂蚁的影响,加强寻优性能。运用插入、逆转变异算子对路径优化,提高解的质量。赵亚文等人[7]把捕食搜索策略与蚁群算法融合,在最优解附近进行搜索,提高寻优潜力。采用更换信息素挥发策略,优化各路径信息素分布,跳出局部最优。彭岳等人[8]将蚁群分为多个蚁群系统,并设置不同的参数来区分蚁群,每个蚁群各自搜索最优路径,多蚁群之间进行交流学习增强寻优能力,增加算法多样性避免陷入停滞。这三种改进的算法提高了跳出局部最优的能力,多样性增加,却没有考虑收敛性能。针对这一缺点,周克良等人[9]运用区域破坏与重建策略提高解的质量;引用2-Opt 算法进行局部优化,解决由于信息素堆积造成的点交叉现象,增加全局搜索的能力,加快算法收敛速度的同时提高算法多样性。袁汪凰等人[10]采用两异构种群并行搜索,并采用奖罚机制进行不同的反馈,平衡算法的收敛速度和多样性。姜道银等人[11]运用信息交流策略对选取的一部分较优路径进行更新,改进解的质量,避免解多样性不足。与此同时该策略通过对部分较优解进行维变量互换得到优质子解,可以加快收敛。这些改进的策略虽然平衡了算法收敛性和多样性,但是对于大规模问题有待进一步改善。
因此,本文提出结合协同机制与动态调控策略的双蚁群算法(dynamic regulation strategy and collaborative mechanism,DCACS)。将蚁群根据适应度值动态划分为导向蚁和合作蚁两个异构双蚁群,运用协同机制两个种群分工合作找到最优解。导向蚁考虑周围信息素的浓度的影响,在路径选择时引入传播因子,降低蚂蚁一直选择某个城市的概率,从而改变蚂蚁的选择,增强寻优性能。合作蚁在局部信息素更新时引入合作算子,受导向蚁中的最优路径的影响,当路径相似度达到阈值,合作蚁启动合作算子,加快算法收敛速度。两个异构双种群分工合作,在保证算法多样性的同时增强收敛性。当所有蚂蚁完成周游时,运用动态调控策略,在全局信息素更新时引入自适应调控算子,对全局最优路径进行正向激励或反向惩戒的调整,不仅加快了算法收敛速度,又能防止算法过早停滞。实验结果表明,本文提出的改进蚁群算法相较传统的蚁群算法在TSP 问题上算法多样性和收敛速度有了明显提高,并且在大规模问题上优势更加明显。
1 前期工作
1.1 蚁群系统
1.1.1 路径选择
蚁群算法(ACS)根据伪随机比例规则选择下一个要遍历的城市j,如式(1):

式中,q0(0 ≤q0≤1)是一个参数,q0值大小影响着对新路径的探索度;q是一个随机变量,分布区间为[0,1];ηij=1/dij代表启发式信息;β是参数,它的大小决定启发式信息在蚂蚁选择城市时发挥的作用;τij表示边(i,j)上信息素的值;J是一个随机变量,如式(2):
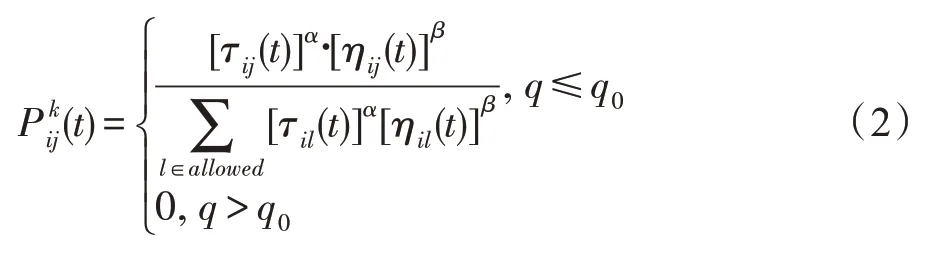
其中,α的大小决定信息素的影响力;allowed代表了位于城市i的蚂蚁k可以选择下个城市的集合。
1.1.2 全局信息素更新
在ACS 中,只有至今最优的一只蚂蚁才被允许在每一次迭代完成后释放信息素,即只有全局最佳巡回路线上的信息素才会得到加固。全局信息素更新机制与式(1)一起使用,是为了使搜索更具针对性。更新规则如式(3):

式中,Lgb表示至今全局最优路径;0<ρ<1 表示全局信息素挥发率;表示增量。
1.1.3 局部信息素更新
局部信息素更新的作用在于:每只蚂蚁遍历完所有城市后,调用式(5)进行局部信息素更新,使得该路径上的信息素会有一定程度的挥发,该路径被选中的概率相对减小,其他路径被探索的几率增大。

其中,0<ξ<1 为局部信息素挥发率;τ0=1/(nCnn)为各边信息素初值,n代表城市数目,Cnn是由最近邻方法得出的路径的长度。
1.2 3-opt算子
3-opt[12]是局部优化的一种常用方法,通过对全局最优解进行优化得到更优解。优化过程通常分为以下几步:(1)选取待优化路径上的任意三条边;(2)断开后尝试与原先不同的连接方式;(3)计算重新连接后的长度并与原路径长度对比,若重新连接后的路径更短,则选用优化后的连接方式。反之,保留原路径;重复(2)、(3),直至完成所有连接方式,其中一种优化方式如图1。

Fig.1 3-opt schematic diagram图1 3-opt示意图
1.3 蝴蝶算法
蝴蝶算法(butterfly algorithm,BA)是Arora等人[13-14]依据蝴蝶觅食等行为的启发提出的一种智能优化算法。每只蝴蝶都可以在空中产生一定强度的气味,散发后被其他蝴蝶感知到,蝴蝶通过感知空气中的气味向着气味浓度大的方向移动,以此来确定食物中心或者伴侣的方向。这就是蝴蝶如何与其他蝴蝶和社会知识网络分享自己的个人信息。香味大小F计算公式如式(6):

式中,γ为幂指数;I为刺激强度;c为蝴蝶感知形式;F为香气的感知强度。
2 改进的蚁群算法
2.1 种群的划分
蚁群算法在求解旅行商问题时对于加快收敛速度与保持路径多样性总是不可兼得,探索过度导致收敛性较差,而学习过快忽略了解的质量。为了协调蚁群间的探索和利用,本文采用异构双种群的结构,将蚁群划分为导向蚁和合作蚁。导向蚁负责探索新路径,提高算法寻优的多样性,避免陷入停滞,合作蚁负责加快算法的收敛速度。为了保证前期算法多样性,后期加快收敛,故随着迭代次数的增多,导向蚁逐渐减少,合作蚁逐渐增加。规定路径长短用适应度值来描述,路径越短表示适应度值越高,每次迭代完根据适应度值进行由高到低的排序,重新划分导向蚁与合作蚁。导向蚁由适应度值较高即路径较短的蚂蚁组成,合作蚁由适应度值较低即路径较长的蚂蚁组成,两蚁群的数量如式(7)、式(8):

式中,m为蚂蚁总数,Nc为最大迭代次数,N为当前迭代数,A、B分别代表导向蚁、合作蚁的数量。x为一比例系数,比例系数的大小影响蚂蚁数量变化速度,如图2。若比例系数过大(如x=1),将会使合作蚁数量增长过快,算法收敛速度加快。但同时解的多样性较差,容易陷入局部最优,得到的是局部最优解。若比例系数过小(如x=5/8),合作蚁增长速度较慢,导向蚁较长时间处于优势地位,导致算法长期处于探索阶段,收敛速度较慢。为了更好地平衡多样性与解的精度,根据实验确定x的取值,实验见3.1.2 小节。

Fig.2 Diagram of the number of ants in different proportion coefficients图2 不同比例系数下蚂蚁数量变化图
图2 为不同比例系数下蚂蚁数量变化曲线图,通过实验测得x取7/8 时算法性能最好。由图2 可以看出,合作蚁的数量与迭代次数呈正相关,导向蚁数量与迭代次数呈负相关,且由图像斜率可以看出整个变化过程两种群蚂蚁数量变化平缓。算法前期导向蚁的数量较多,发挥主导作用,保证路径的多样性,提高解的质量;算法后期合作蚁的数量较多,合作蚁发挥主要作用,加快收敛。为了保证导向蚁可以继续探索,避免陷入局部最优的困境,最后一次迭代时导向蚁的数量仍为蚂蚁总数的
2.2 协同机制
协同是两个或两个以上的个体或群体共同朝着某一目标前进,且两者相互配合产生的效果大于各个个体单独作用时的总和。故本文引入协同机制,把蚁群划分为异构双蚁群:导向蚁和合作蚁,双蚁群分工协作寻找最优路径。导向蚁职能是扩大搜索范围,开发新路径;合作蚁职能是提高算法收敛性能。引入协同机制把两个蚁群联系在一起,达到合作交流、信息共享、相互促进的目的,使得算法能够更快地找到全局最优解,同时保证算法多样性,避免算法过早陷入停滞状态。
2.2.1 传播因子及传播域
若某路径在之前的迭代中多次出现,出现频率较高,这些路径上的信息素会逐渐积累,最终得到的这个解往往是局部最优解,且这种局部最优不易跳出。为了避免算法过早收敛于某个局部最优解,造成算法早熟,将蝴蝶算法的思想引入导向蚁中,扩大搜索范围。导向蚁在选择下一个城市时可以感知周围路径上的信息素,把这种影响定义为传播因子f,计算公式如式(9):

式中,i为当前蚂蚁的位置,j为蚂蚁将要访问的城市,Δτij为路径(i,j)上的信息素;为以i为圆心的区域中所有可访问节点的路径信息素总和;n为以i为圆心的区域中可以访问的城市个数。导向蚁在以i为圆心的区域中,到所有可访问节点的信息素总和是一定的。要访问城市不同,边(i,j)上的信息素量不同。当边(i,j)上信息素值较小时,边(i,j)上的信息素量与邻域信息素总和差值较大,传播因子f的值越大。
引入传播因子后的状态转移规则如2.2.2 小节的叙述。当路径(i,j)上的信息素值较大时,即与邻域信息素总和差值较小时,传播因子的值较小,使得当前最优城市被选择的概率较没有引入传播因子时减小;当路径(i,j)上的信息素较小,即与邻域信息素总和差值较大时,传播因子的值较大。使得蚂蚁在选择下个城市时能跳出当前最优城市,转换目标,增大较优城市被选择的概率,扩大搜索路径,提高算法多样性。
文献[6]借鉴贪心算法的思想,在概率选择公式中引入间接期望启发式及相应的启发式因子即考虑当前节点到其他节点距离的均值对路径构建的影响,增加算法多样性。文献[10]通过设置奖惩模型,对学习后较差的种群进行惩罚,增加种群多样性。文献[15]引入探索率因子,通过对全局概率选择方式进行修正,增大信息素较弱的路径被选择的概率,增强搜索能力。这些改进方式对于小规模问题而言算法多样性整体得到了提高,但对于大规模问题,随着信息素的积累,算法在中后期依然容易陷入局部最优,解的精度并没有改善。
因此,本文借鉴蝴蝶算法的思想在导向蚁构建路径时引入传播因子。算法前期路径信息素差距不大,传播因子的引入可以平衡各路径被选择的概率,使蚂蚁移动的随机性增强,扩大搜索范围,达到提升算法多样性的目的。在算法中后期,特别是对于大规模城市而言,路径信息素差距增大,导致选择可能会被局限在某个城市上,陷入局部最优。传播因子的引入可以降低出现次数最高的城市被选择的概率,提高较优路径被选择的概率。深入挖掘潜力值较高的路径,避免了算法由于当前路径信息素浓度影响力过大而陷入局部最优,从而提高解的质量。
考虑到蚂蚁进行路径选择时除了受信息素浓度的影响,还受到两城市之间路径长短的影响,因此距离过大的城市即使考虑进去也不会作为下一个访问的节点。为了进一步节省程序运行时间,提出传播域的概念。但是传播域过小往往会忽略掉潜在最优,在一定程度上抑制了算法的多样性,不能保证解的质量。最终经过多次实验分析得到传播域的定义:
以i为圆心,r为半径画圆得到圆形传播域,半径r大小如式(10):

式中,n表示可以访问的城市的总数,din表示城市i到城市n的距离。
本文选取的TSP 城市数目较多且分布比较紧密,同时半径r的选择相对较大,保证了解的质量。传播域之外的城市到i点的距离较长,最终也不会考虑其作为下一个要遍历的地方。因此传播域在保证解的质量的同时减少了程序的运行时间。
2.2.2 改进的状态转移规则
导向蚁中的蚂蚁在选择下一个城市时除了受ηij、τij这两个参数的影响外,还要考虑传播因子f产生的影响。考虑到周围信息素的影响引入传播因子,使得导向蚁在进行路径选择时增大较优路径周围城市被选择的概率,扩大搜索范围。改进后的路径选择规则如式(11):

在经典ACS 算法中,各路径信息素初始值相同,前期主要依据城市之间的距离选择下个节点,随着迭代次数的增多,局部距离较短的路径上信息素浓度过高,导致选择范围减小,陷入停滞状态,难以得到更优解。传播因子的引入影响城市被选择的概率,若当前城市i到下一城市j路径上的信息素浓度与周围信息素浓度总和相差较小时,受周围信息素浓度的影响较小,使得城市j被选中的概率比不考虑传播因子时被选中的概率减小。因此传播因子的引入使得原先被选中概率大的城市概率减小,从而调整选择的目标,增加探索未使用过的边的机会,提高算法多样性,避免算法前期由于启发式信息发挥主要作用造成信息素积累而陷入局部最优的问题。
2.2.3 路径相似度
所有的导向蚁进行局部信息素更新后,合作蚁按照ACS 的规则开始路径构建,在局部信息素更新之前,每只蚂蚁都要与导向蚁中的最优路径计算路径相似度S。通过建立数学模型来求解路径相似度:Route_Abest为导向蚁中最优路径构成的位置矩阵,如式(12)。Route_Bk为合作蚁中第k个蚂蚁路径构建完得到的位置矩阵,如式(13)。导向蚁的最优路径与第k个合作蚁的公共路径用Same表示,如式(14)。最后路径相似度S的计算公式如式(15):

式中,Same表示公共路径;numberSame表示导向蚁的最优路径与第k个合作蚁相同路径的个数;r表示城市数。当第k个合作蚁得到的路径与导向蚁的最优路径重复率较高时,即路径相似度达到阈值时,合作蚁进行局部信息素更新时启动合作算子,使得当前合作蚁构建的路径上保留的信息素量增多。这一过程导向蚁发挥了引导作用,加强了两蚁群之间的合作,从而加快算法的收敛速度。
2.2.4 基于合作算子的局部信息素更新
当路径相似度达到阈值时,合作蚁进行局部信息素更新时引入合作算子σ,如式(16)、式(17):
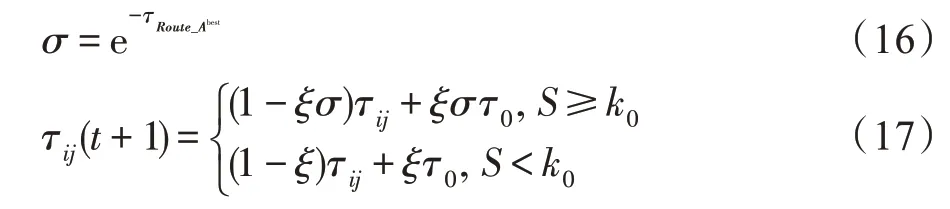
局部信息素更新的目的是通过信息素的挥发限制较优路径信息素的积累,增加多样性。由式(16)可看出,合作算子0<σ<1。引入合作算子后,使得信息素的挥发系数在[0,0.1]之间动态变化。合作算子与导向蚁中最优路径上信息素总量有关,信息素积累得越多,说明该路径越优,合作算子σ值就越小,进而合作蚁中局部信息素挥发率越小,达到加快信息素积累的目的。当合作蚁与导向蚁的最佳路径相似度达到阈值,合作蚁在局部信息素更新时会启动合作算子,合作蚁进行局部信息素更新时路径上信息素的挥发量比没有引入合作算子挥发量减少,即路径上剩余的较原来多。加快算法的收敛速度,使得信息素的正反馈作用得以体现。且在算法后期合作蚁占据主导地位,进一步提升了算法收敛性能。
2.3 动态调控策略
导向蚁与合作蚁都完成路径构建后,运用动态调控策略进行全局信息素更新。当此次迭代导向蚁与合作蚁都遍历完成,蚁群的全局最优路径都要被检测,即此次迭代得到的最优解与全局最优比较:若第t次迭代得到更优解,表明此时路径上的信息素分布更具指导性,进行全局信息素更新时实施正向激励,加快收敛;若第t次迭代得到的最优解劣于全局最优解,表明该当前路径信息素分布没有指导作用,进行全局信息素更新时实施反向惩戒,减少信息素积累,避免陷入停滞状态;若第t次迭代得到的最优解与全局最优解相同,信息素更新规则不做变动。由此引入适应性调控算子U,如式(18)、式(19)。改进的全局信息素更新公式如式(20)。

式中,N为当前迭代数;global_best为前(t-1)次的最短路径,即全局最优;length_best(t)表示第t次迭代产生的最短路径。由式(18)、式(19)可以看出,适应性调控算子与迭代次数和路径长度有关,随着迭代次数的增大而减小,且随着两个最优路径差值的增大而减小。前期适应性调控算子的值较大,影响较大,使信息素更具导向性。后期迭代次数N值较大,适应性调控算子值较小,对更新机制产生的影响也较小,避免U产生的影响过大使算法陷入局部最优。由式(20)可以看出,当第t次迭代找到更优解时,适应性调控算子U发挥正反馈作用,加快收敛。当第t次迭代找到的最优解与全局最优相同时,适应性调控算子U不发挥作用即不做任何改变。当第t次迭代找到的最优解劣于全局最优时,适应性调控算子U发挥负反馈作用,调节路径上的信息素,增加次优路径被选中的几率,避免算法陷入停滞状态。
2.4 算法性能分析
蚁群算法的改进主要是提高算法多样性、加快收敛速度这两方面的性能,但是往往改进的单种群蚁群算法不能兼顾两方面的性能,一方面的性能得到了提高,另一方面性能会变差。为了平衡两者之间的矛盾,把蚁群动态地划分为异构双蚁群:导向蚁、合作蚁,两蚁群在迭代过程中执行各自的任务。导向蚁在路径构建时,若当前城市到下一城市信息素浓度较高,受邻域信息素的影响该城市被选中的概率较之前低;反之,若当前城市到下一城市信息素浓度较低,该城市被选择的概率较之前略有提高。以此增大次优城市被选中的概率,扩大搜索范围,扩展新路径提高算法多样性。当所有导向蚁构建完路径后合作蚁开始构建,每个合作蚁构建的路径都要与导向蚁中的最优路径进行比较,当路径相似度达到阈值时,合作蚁进行局部信息素更新时启动合作算子,使得路径上信息素挥发量减少,积累量增多。发挥信息素的导向作用,加快收敛。两蚁群相互合作以平衡算法收敛速度和解的多样性。
从全局来看,导向蚁与合作蚁随着迭代次数动态变化,前期导向蚁数量多于合作蚁,导向蚁发挥主要作用增加解的多样性。随着迭代次数的增加,导向蚁数量逐渐减少,合作蚁数量增多,合作蚁发挥主要作用使得较优路径上的信息素快速积累,加快收敛,得到最优路径。
在全局信息素更新规则中引入适应性调控算子U进行调控。若此次迭代出现更优路径,调控算子则对该路径信息素进行正反馈调整,即对该最优路径信息素进行奖励,使信息素更具导向性,加快算法收敛。若此次迭代得到的路径较差,调控算子则在全局信息素更新时对最优路径信息素进行惩罚,减少最优路径信息素的积累,使潜在最优路径被选择的概率增大,提高路径多样性。前期适应性调控算子的值较大,影响较大。后期迭代次数较大,适应性调控算子值变小,对更新机制产生的影响也较小,避免产生过大的影响使算法陷入局部最优。达到了通过控制调控算子来平衡收敛速度与多样性的目的。
2.5 算法流程图
DCACS 算法流程图如图3。首先对蚁群划分,第一次迭代时所有蚂蚁划分为导向蚁,导向蚁在路径构建时引入传播因子,扩大搜索范围。每次迭代完后根据蚂蚁的路径优劣根据式(7)、式(8)把蚂蚁分为导向蚁与合作蚁,标记路径较好的蚂蚁为导向蚁,其余为合作蚁,且随着迭代次数的增多导向蚁的数量是逐渐减小的。合作蚁会受到导向蚁中最优路径的影响,当路径相似度达到阈值时,合作蚁启动合作算子,使得路径上保留的信息素量增多,发挥导向作用,加快收敛。最后运用动态调控策略进行全局信息素更新,对全局最优路径上的信息素进行正向激励或反向惩戒,从而实现算法多样性与收敛性的平衡。

Fig.3 Algorithm flow chart图3 算法流程图
2.6 算法复杂度分析
从图3 DCACS 的流程图分析可看出,两蚁群搜索过程是相互独立的,故DCACS 的最大时间复杂度为O(m×r×1+(m1×r+m2×r)×(Nc-1)),其中m为蚂蚁总数,m1、m2分别为导向蚁、合作蚁的数量,r为城市数,Nc为最大迭代次数,经计算得到改进后算法的最大时间复杂度为O(m×r×Nc),与原算法ACS的相同。因此本文算法没有增大复杂度,且本文提出的DCACS 算法在收敛性与寻优性方面较经典算法有明显的提高。
2.7 算法收敛性分析
在DCACS 算法中,因为信息素的蒸发作用,信息素水平的最大限制τmax是渐进受限的。为了便于计算,把DCACS 算法中的两种信息素更新机制统一记 作τij(θ+1)=(1-φφ)τij(θ)+φφb,当φ=ξ,φ=σ,b=τ0时表示局部更新机制;当φ=ρ,φ=1,b=qf(sbs)时表示全局更新机制;最后计算出τij(θ)=(1-φφ)θτ0+b[1-(1-φφ)θ],当θ→∝时,由于τ0为初始值,故τmin=τ0。
由于信息素存在上下界,确保了式(11)中任一概率pmin>0 。若蚂蚁访问下个城市j时,路径(i,j)上的信息素量与启发式信息乘积的结果不是最大值,则选中该边的概率为,在ACO 算法中pmin下 界为。因此对无穷大的θ和任意小的正数ε,P*(θ)≥1-ε成立,θ表示迭代次数,P*(θ)表示最少一次得到最优路径的概率,根据以上可得。因此只要保证迭代次数,DCACS 算法值是收敛的且概率为1。
3 实验仿真
为了检验改进后算法DCACS 的收敛性和寻优能力等,本文使用Matlab2017a软件进行仿真。
3.1 参数设置
3.1.1 参数说明
实验中用到的参数有m、α、β、ρ、ξ、q0、k0,其中m为蚂蚁的数量,当蚂蚁数量过多时,m只蚂蚁并行搜索,全局搜索能力增强,较优路径信息素比较平均,信息素导向作用不强,导致算法收敛速度较慢;当蚂蚁数量较少时,对于大规模城市,搜索能力差,得到的解的质量不高。α为信息素的影响因子,α值越大,信息素的导向作用越明显,但值过大会导致算法过早陷入局部最优。β为期望启发式的影响因子,值越大,蚂蚁在选择下个城市时选择局部最短路径的概率越大,导致算法多样性和解的质量较差。ρ和ξ分别表示全局信息素、局部信息素挥发率,挥发率的大小影响着算法收敛速度。q0为伪随机因子,其大小影响着对新路径的探索度。q0越小,蚂蚁探索新路径的概率越大,同时收敛速度较慢;反之,q0越大,蚂蚁集中搜索至今最优路径,虽然提高了收敛速度但是搜索能力变差,得到的解的质量不高。k0为启动合作算子的阈值。当k0设置过小,导致路径相似度较小时就可以跟随导向蚁的最优路径,算法过早收敛,易陷入停滞状态;当k0设置过大,收敛速度较慢。
3.1.2 参数确定
3.1.2.1 经典参数的确定
正交实验是研究多因素、多水平组合的一种实验方法,利用正交表进行实验设计,通过少量的实验代替全面的实验。故本文采用五因素四水平的正交实验来确定经典算法ACS 的参数α、β、ρ、ξ、q0的取值,各因素水平如表1。以kroA100 为实验对象,每组进行10 次实验,统计每个组合方案的平均解,制定的L16(45)正交表及测试结果见表2。根据各因素水平下的平均解的总和确定最优方案,实验结果分析见表3。

Table 1 Level table of each factor表1 各因素水平表
总和表示同一水平下的所有平均解之和,平均值表示各水平的均值。由表3可看出,当α=1,β=4,ρ=0.3,ξ=0.1,q0=0.8 时,平均路径最短。
经过多次实验参数的调节与数据统计发现经典算法ACS 设置为表4 中的数据时效果最好。作为对比实验,ACS+3opt 与DCACS 算法选用与经典算法ACS 相同的数据。
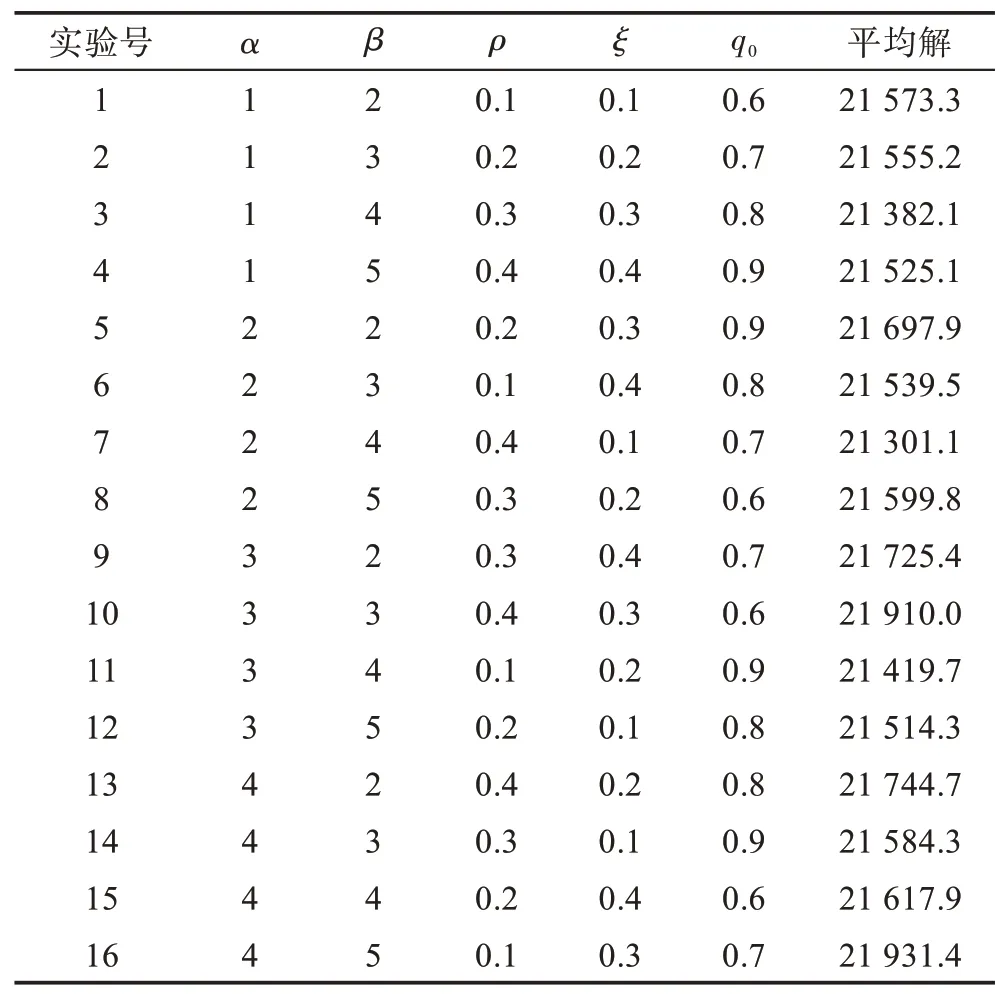
Table 2 Test scheme and test results表2 测试方案与测试结果

Table 3 Analysis of test results of each parameter表3 各参数测试结果分析

Table 4 Setting of parameters表4 参数设置
3.1.2.2 k0 的确定
k0的选取影响收敛速度,为了确保算法性能,本文设置一个对比实验,k取不同值时比较收敛效果与解的精度。实验选取不同规模的测试集eil51、ch150与a280 作为代表,分别进行15 次实验,根据收敛速度与解的质量确定k0的值。
由图4 可看出,当k0取值较小时(如k0=0.1),导致测试集在前期收敛性过强,算法很快就得到最短路径。这是由于路径相似度阈值k0取值较小时,启动合作算子跟随导向蚁中的最优路径,随着信息素的积累,陷入停滞状态,这时得到的最优路径属于局部最优路径。当k0的取值过大(如k0=0.8),算法收敛性较差,得到的解的质量也不高。这是由于k0取值较大,合作蚁构建的路径与导向蚁中的最优路径相似度较高时才能启动合作算子,最优路径上的信息素导向性不强。图5 为3 个规模的测试集在k0取不同值时得到的最短路径。根据图4、图5的结果可看出,对于这三种规模的城市,当k0=0.4 时,得到的解最优,收敛性最好。综上,阈值k0设为0.4最为合适。
3.1.2.3 比例系数x 的确定

Fig.4 Convergence graph for different values of k0图4 k0 取不同值时的收敛图

Fig.5 Optimal path for different values of k0图5 k0 取不同值时的最优路径
由式(7)、式(8)可知,导向蚁与合作蚁的数量是动态变化的,合作蚁的数量随着迭代次数的增加而增加。最后一次迭代时导向蚁的数量为m-[xm],合作蚁的数量为[xm]。其中导向蚁的职责是探索新路径,合作蚁职能是加快收敛。为了更好地提升算法性能,本文设置一比例系数x来控制两蚁群的数量变化,其中x≤1。若x设置过大,将会使合作蚁数量增长过快,使算法过早陷入局部最优,最后得到局部最优解。若x设置过小,合作蚁数量增长过慢,会使得算法收敛速度较慢。本文以测试集eil51 为例,x的设置情况如图6 所示。从整体看,当x取值小于1 时,算法的寻优结果优于x=1 的情况。当x取值较大(如x=1),后期合作蚁增长过快,导向蚁发挥作用减弱,虽然收敛速度加快,但是陷入了局部最优。而x设置较小时(如x=1/16),合作蚁的数量增长过慢,导向蚁数量一直多于合作蚁,导向蚁发挥主要作用,收敛速度过慢,算法得不到最优解。x取时,能得到最优解,但是在1 000 代左右才收敛,收敛效果有待提升。综合考虑收敛速度与搜索能力两项指标,当x=7/8 时,收敛速度最快,解的质量最高,故比例系数设为7/8 时最为合适。

Fig.6 Iteration with different proportional coefficients图6 不同比例系数下迭代情况
3.2 改进策略分析
3.2.1 传播因子多样性分析
为了验证引入传播因子对算法多样性的影响,选用规模kroB150 作为测试集进行分析。因为熵是对不确定性的一种度量方式,熵值越大,代表系统的不确定性越大,算法多样性越好。故本文用熵分析ACS 算法和引入传播因子后算法的多样性,传统ACS 算法与ACS+传播因子(引入传播因子的ACS 算法)多样性如图7 所示。为了更明确比较两者的熵,设置断点对比两个算法的多样性,结果如图8。
由图7 多样性对比结果可以看出,引入传播因子后的ACS 算法的熵的平均值在5.4 左右。ACS 算法熵的平均值在5.0 左右,说明引入传播因子后的ACS算法有效提高了算法多样性。图8 为算法每间隔50代设置断点计算的熵值,可以看出加入传播因子后的ACS 算法熵值整体都高于ACS 算法。在500~1 000 代时,两种算法差距明显,这是由于刚开始迭代时各路径信息素初值相同,初期受周围信息素影响较小;随着迭代次数的增多,各路径信息素量差距变大,传播因子发挥作用,蚂蚁受周围信息素的影响,降低局部最优城市被选中的概率,增大其他边探索的机会,从而提高算法多样性。
3.2.2 合作算子收敛性分析
为了验证合作算子对算法收敛速度的影响,本文选取小规模城市eil76、中规模城市kroA200、大规模城市lin318作为代表进行分析。改进的算法DCACS与DCACS-1(缺少合作算子的DCACS 算法)收敛情况如图9。

Fig.7 Comparison of kroB150 diversity results图7 kroB150 多样性结果对比

Fig.8 kroB150 entropy comparison图8 kroB150 熵值对比
由图9 可以看出,加入合作算子后,对于小规模城市eil76,加入合作算子后的算法在350 代左右就找到了最优解,而DCACS-1 在500 代左右才得到最优解,加入合作算子后比缺少合作算子的算法可以更快地找到最优解。对于中大规模城市,收敛速度也明显优于DCACS-1。
3.2.3 动态调控策略性能分析
为了验证动态调控策略中适应性调控算子U对算法的影响,选用kroA100 作为代表进行分析,比较DCACS 与DCACS-2(缺少适应性调控算子的DCACS)的收敛速度,结果如图10。
由图10 可以看出,DCACS(有适应性调控算子)算法在600 多代就已经找到了最优解,而DCACS-2(缺少适应性调控算子的DCACS)直到1 200 多代才找到最优解。在寻找最优路径过程中DCACS 算法的收敛速度明显优于DCACS-2 算法。这是由于对全局最优路径进行信息素更新时引入了适应性调控算子,通过对路径上的信息素进行正向激励或反向惩戒,使得路径上的信息素更具有指导性,进而加快算法收敛。
3.3 DCACS 个体分布情况分析
为了更细致地观察异构双蚁群在不同时期发挥的作用,以eil51为测试集进行测试,结果如图11、图12。
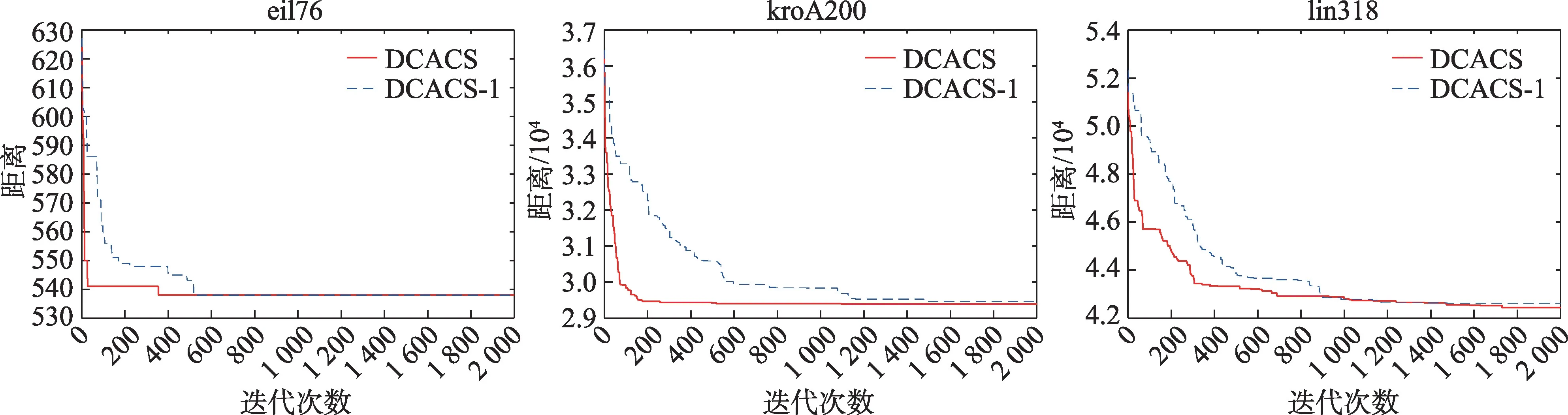
Fig.9 Comparison of convergence between DCACS and DCACS-1图9 DCACS 与DCACS-1 收敛性对比

Fig.10 kroA100 iteration图10 kroA100 迭代情况

Fig.11 Ants distribution at different times图11 不同时期蚂蚁数量分布图
图11 为不同迭代时期蚂蚁数量分布,图12 为在与图11 相同迭代时期时DCACS 算法与ACS 算法的熵。熵值越大,解的多样性越好。整体来看,当迭代次数小于800 时,导向蚁数量多于合作蚁,导向蚁占主导地位。当迭代次数高于800 时,合作蚁占主导地位。由图11、图12 可知,当迭代次数小于200 时,导向蚁占比较高。DCACS 与ACS 的熵值相差不大,这是由于初始阶段各路径信息素相差不大,导向蚁中的传播因子的作用还不明显,处于初步探索阶段。在200~400 代,DCACS 与ACS 的熵值都略有提高,且DCACS 的熵值整体高于ACS。这是由于这个阶段导向蚁一直处于主导地位,随着迭代次数的增加,各路径信息素差距开始变大,传播因子开始发挥作用,扩展了新路径,丰富了算法的多样性。在400~800 代之间,导向蚁的数量逐渐减小,在800 代左右两蚁群数量相当。这阶段DCACS 的熵值快速增长,在800代左右达到最大。说明算法在这阶段仍处于探索阶段,随着信息素的积累在800 代左右信息素影响力度达到最大,传播因子发挥作用明显,使得算法多样性达到最好。在800~1 200 代之间,合作蚁数量超过导向蚁,合作蚁开始占主导地位。DCACS 的熵值开始减小,说明解的多样性开始减小,算法进入收敛阶段。这阶段ACS 的熵值保持稳定,整体低于DCACS的熵,说明在算法中期虽然合作蚁发挥主要作用,但导向蚁仍会继续探索,避免算法过早陷入停滞状态。在算法中期的1 200~1 600 代到算法后期的1 600~2 000 代,这两个阶段合作蚁数量逐渐增加,DCACS算法熵值持续下降。说明合作蚁中合作算子的引入使得路径信息素挥发量减少,加快了信息素累积,进一步加快了算法收敛。且在中后期DCACS 的熵值仍高于ACS,表示算法后期导向蚁在提高多样性方面仍起到了一定的作用,增加了跳出局部最优的可能。
3.4 与经典算法对比分析
3.4.1 实验结果分析
为了有效地验证改进算法(DCACS)的收敛性及解的质量等性能,本文选取eil51、eil76、kroA100、ch150、kroB150、kroB200、tsp225、a280、lin318 等中大规模TSP 算例来进行分析,以这些城市为实验对象,分别对ACS、ACS+3opt 及DCACS 进行15 次实验,同时从最优解、平均解、误差率、收敛速度几个方面进行比较。误差率计算公式如下:

Lbest表示三种算法得到的最优解,Lmin表示标准解。
由表5结果可以看出,对于eil51、kroA100、kroB150等中小型城市,改进后的算法得到最优解时所需的迭代次数更少,平均解也优于ACS 和ACS+3opt 这两种经典算法;对于kroA200、tsp225、a280、lin318 等大规模城市,DCACS 得到的最优解、平均解及误差都优于ACS 和ACS+3opt,且误差均在1%以内。综上,DCACS 算法的误差率、收敛性都优于经典算法,且得到的解的质量也较好。本文算法融合协同机制及动态调控策略,不仅提升了寻优能力,避免了算法过早陷入停滞状态,还提高了收敛速度,因此DCACS 能够有效平衡算法多样性和收敛速度之间的矛盾。

Table 5 Simulation experiment data of ACS,ACS+3opt and DCACS表5 ACS、ACS+3opt和DCACS 仿真实验数据
3.4.2 收敛性对比分析
在ACS、ACS+3opt、DCACS 三种算法中分别进行了15 次实验,统计得到实验数据。图13 为选取的部分小、中、大规模测试集的最佳巡回路径。图14 为DCACS 与ACS、ACS+3opt收敛速度对比。
由图14 可以得出,对于eil51、eil76 等小规模城市,虽然改进的DCACS 算法、ACS 算法 及ACS+3opt算法都可以找到最优解,但是DCACS 在200 代至600代就得到最优解,而经典算法在1 000 代甚至1 400代左右才得到最优解。对于中规模、大规模测试集,DCACS 算法找到的最优解不仅优于ACS 和ACS+3opt 算法,且DCACS 算法得到最优解时的迭代次数更少。异构双蚁群分工协作、信息共享不仅加快收敛,而且提高了解的质量。
3.5 与其他最新的改进蚁群算法对比
为了进一步验证改进DCACS 算法性能,选用最新改进的蚁群算法IACA、D-ACS、CACS 与本文算法进行比对,结果如表6。其中面向旅行商问题的蚁群算法改进(IACA)来自于文献[16],改进的算法D-ACS来自文献[17],融合猫群算法的动态分组蚁群算法CACS数据来自文献[18]。由表6可以看出,DCACS 算法得到的解的质量对于小规模城市、中规模城市和大规模城市都优于D-ACS、IACA 和CACS 三种算法,对于大规模城市尤为明显。本文改进后的DCACS算法与经典的蚁群算法ACS、ACS+3opt 和某些最新改进的蚁群算法相比,解的质量和算法收敛性能都有了明显的提升。
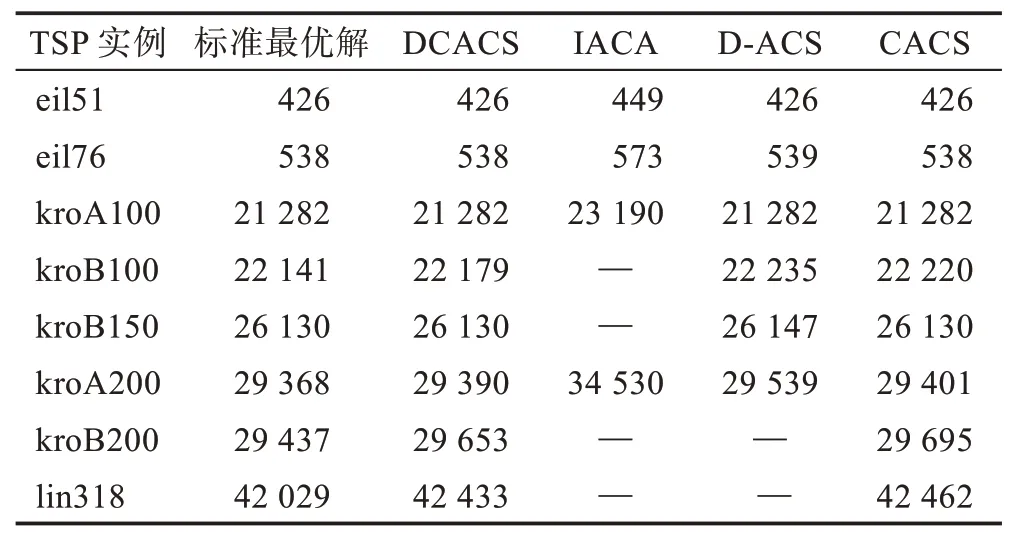
Table 6 Comparison of DCACS with other newly improved algorithms表6 DCACS 与其他最新改进算法比较

Fig.13 Optimal path diagram for part of test set图13 部分测试集的最优路径图

Fig.14 Convergence comparison among DCACS,ACS and ACS+3opt图14 DCACS 与ACS、ACS+3opt收敛对比
4 结束语
本文针对蚁群算法在求解TSP 问题时存在的寻优能力与收敛性较差的问题,提出了结合协同机制与动态调控策略的双蚁群算法。将蚁群随着迭代次数动态划分为导向蚁和合作蚁:导向蚁在路径构建过程引入传播因子,增大其他路径被探索的几率;合作蚁则考虑构建的路径与导向蚁中最优路径的相似度,当达到阈值时,跟随导向蚁的最佳巡回路径,启动合作算子,加快收敛。最后引入动态调控策略,加入适应性调控算子,对全局最优路径进行正向激励使得路径信息素更具导向性,进一步加快算法收敛速度。对全局最优路径进行反向惩戒,均衡路径信息素分布,防止陷入局部最优。仿真结果表明,对于大规模城市,算法在解的质量及收敛性方面都有了很大的提高,算法多样性也得到了明显改善。以后将研究多蚁群算法合作模型,进一步提高寻优性和收敛性。

