探索拓扑编码中的图格与传统格的联系
张明军,杨思华,姚 兵
1.兰州财经大学 中国西北金融研究中心,兰州730020
2.兰州财经大学 信息工程学院,兰州730020
3.甘肃省电子商务技术与应用重点实验室,兰州730020
4.西北师范大学 数学与统计学院,兰州730070
1 研究背景及预备知识
1.1 格密码
研究发现,格(lattice)理论在密码分析和设计中有着广泛的应用,由于格上的运算大多是线性运算,基于格理论的格密码是一类抗量子计算攻击的公钥密码体制[1]。因此,利用格理论所构建的新型公钥密码体质比现有方案运算速度更快[2]。清华大学的密码专家王小云等人在文献[2]中总结到:(1)格密码学(lattice cryptology)的学科交叉所带来的许多数学问题不仅成为密码领域重点研究的内容,也被数学领域与计算机科学领域所关注。(2)格密码体制(lattice cryptosystem)的体制安全性基于NP-Hard、NP-C 问题,目前还不存在解决某些格困难问题的多项式量子算法,使得格密码体制成为抗量子攻击的密码体制中最核心研究领域。(3)由于格运算具有同态(homomorphism)特性,因此设计格同态加密密码体制对于解决安全云计算环境下的密文检索、加密数据处理等方面具有潜在的应用价值。
一个格是m维欧式空间Rm的n(m≥n)个线性无关向量组的所有整系数线性组合,即:

称B为格基(lattice base),m称为格的维数,n称为格的秩,且满足m=n的格称为满秩的。格是欧式空间Rm中一类具有周期性结构离散点的集合,同一个格可以用不同的格基表示。为防止混淆,以下称式(1)中的格L(B) 为传统格(traditional lattice)。当格基B中每个向量的分量为非负整数,每个系数xi为非负整数时,得到非负整数传统格,特记为L(Z0B)。
受格密码体制是具有抗超大计算机和量子计算的功能启发,文献[3-4]引进了图格的概念,它们的建立是基于拓扑图和图运算,或者由拓扑编码和图运算来建立。然而,关于图格的研究结果很少。本文将借助文献[5]和文献[6]中的Topsnut-图形编码、Topcode-矩阵Tcode、图格以及图同态格等技术,利用混合图的着色和优美标号后的优美全着色来构造新而特殊的着色图格,尝试为拓扑图编码提供新的有效算法,并证明这些图格对特殊着色具有封闭性。将定义特殊着色图的拓扑向量,尝试建立图格与非负整数传统格之间的联系,尝试将传统格理论的一些技术移植到图格上。
已知图格的应用场景有:(1)软件、网络结构的相似研究,确定它们结构的相似程度,为克服网络和软件的脆弱性、漏洞、缺陷提供参考技术。例如,图格中的任何两个图的结构都具有图格基相似,图格对一些图运算、编码是封闭的,使得图格中的图可以为实际应用提供结构性能好的软件、网络模型。(2)由于图格中的图无穷多,可以为网络的整体加密提供更多的可选的拓扑编码。此外,拓扑编码容易产生字节数很长的文本密码。(3)汉字拓扑编码是拓扑编码的分支,它可直接用汉字生成文本密码,方便使用汉语的人们。(4)图格中图的汉字图分解涉及到汉语的拓扑图化研究,以及汉语密码体制的建立[7]。(5)给数学学科和计算机学科提供新对象、新问题,力图为格理论打造新的分支。此外,图格中的Topcode-矩阵具有同态特性,与图格同类的格是图同态格、度序列格、Topcode-矩阵格等。对它们的研究必将促进学科的发展。
1.2 数字串拓扑认证问题及其复杂度分析
数学的拓扑图可以自然地表示一些编码关系的结构,也叫作拓扑编码(topological coding),这种关系结构在许多研究领域里得到应用。拓扑编码中有如下一个问题:
数字串拓扑认证问题(number-based string topological authentication problem,NBSTAP)。给出一个数字串s(n)=c1c2…cn(as a public-key),其中ci∈[0,9]={0,1,…,9},找到一个图Q(as a private-key),使得图Q的一个数学特征恰由数字串s(n)中的数字构成,使得s(n)中的每个数字ci被用到,且只用到一次。
显然,数字串s(n)=c1c2…cn可用于口令认证或文件加密。下面给出解释NBSTAP 的例子。
例1给出一个数字串s(15)=555544332222110,可以将它写为数字序列d1=(5,5,5,5,4,4,3,3,2,2,2,2,1,1,0),也可以将它写为数字序列d2=(12,10,5,5,5,5,4,4,3,3,2,2,2)。用记号deg(P)表示一个图P的度序列(degree sequence),由图1 可知,数字序列d1、d2皆为某些图的度序列,d1=deg(G)=deg(G1),d2=deg(H)=deg(H1)。不难看到,图G和图G1完全不同构,即G≇G1;同理,有H≇H1。这4个图都是NBSTAP的解。
再将数字串s(15)写成3 个向量X=(2,2,2,1,0),E=(1,2,3,4,5)和Y=(3,4,5,5,5),用它们构造出一个叫作Topcode-矩阵Tcode(T)=(X,E,Y)T,如图1 所示。用矩阵Tcode(T)确定出一个着色图T(也叫作Topsnut-图形编码,见图1),完成数字串s(15)的拓扑认证。
例2将数字串s(33)=51662453894555106600778 8009910100 写成3 个向量X′=(5,4,5,5,5,0,0,0,0,0),E′=(1,2,3,4,5,6,7,8,9,10)和Y′=(6,6,8,9,10,6,7,8,9,10),得到如下的Topcode-矩阵Tcode。

然而,式(2)中的Topcode-矩阵Tcode是图2 中的6个Topsnut-图形编码共有的Topcode-矩阵,且这6 个Topsnut-图形编码的拓扑结构互不同构。
例3数字串与多种类型的矩阵关联:
(1)根据国家标准GB2312-80[8],“人人好公则天下太平”这句话的汉字序列为G*=H4043H4043H2635H2511H5282H4476H4734H4411H3829,它的汉字GB2312-80-矩阵Ahan(G*)在式(3)中给出。

Fig.1 Examples for illustrating NBSTAP图1 解释数字串拓扑认证问题的例子

Fig.2 6 Topsnut-graphical password图2 6 个Topsnut-图形编码
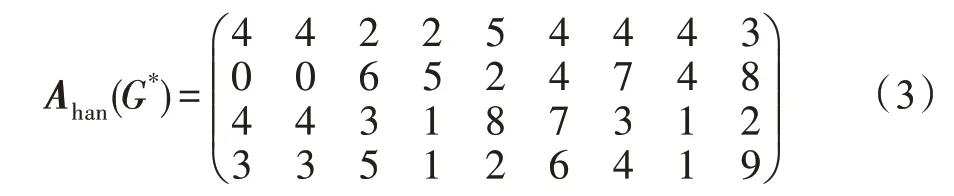
(2)图3 给出Topsnut-图形编码G的相邻矩阵A(G)和Topsnut-矩阵B(G)。
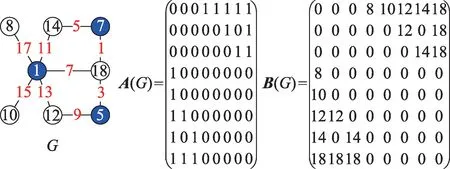
Fig.3 Topsnut-graphical password G and its own adjacency matrix A(G)and Topsnut-matrix B(G)图3 Topsnut-图形编码G 及其相邻矩阵A(G)和Topsnut-矩阵B(G)
通过上面的例子,有如下的NBSTAP复杂度分析:对一个数字串s(n)=c1c2…cn(ci∈[0,9]={0,1,…,9}),有:
①数字串s(n)对应的图Q的数学特征不唯一。例1、例2 和例3 指出:数字串s(n)可以确定图的度序列和相邻矩阵,也可以写出Topsnut-图形编码的Topcode-矩阵和Topsnut-矩阵。度序列和矩阵是两个本质不同的数学概念,Topcode-矩阵和Topsnut-矩阵与图的编码有关,然而,没有写出数字串s(n)所对应的全体矩阵的多项式算法。
②用数字串s(n)写出的度序列不唯一。没有研究报道写出一个数字串s(n)所对应的全体度序列相关算法。
③数字串s(n) 确定的度序列所对应的图不唯一。如果数字串s(n) 确定的全体m(s(n)) 个度序列degk(s(n))=(ak,1,ak,2,…,ak,mk)(k∈[1,m(s(n))])都能找到,用这些度序列degk(s(n))来画出全体互不同构的图要遇到判断图同构(graph isomorphism)这个NP-hard 问题。当n较大时,判断互不同构图的计算量是指数级别。例如,当n=24 时,要判断不少于2197个互不同构的24 个顶点的图(据报道,地球上的沙子的颗粒数目大约有276~278粒)。目前,没有学术界认定的判断图同构的多项式算法。
④数字串s(n) 确定的Topcode-矩阵所对应的Topsnut-图形编码不唯一。图形编码的新技术不断涌现,已知有超过350 种着色技术(文献[9]列出的着色超过200 余种)。图论学科中的许多着色技术含有未解决的数学难题,例如:优美树猜想、全着色猜想、顶点可区别边着色猜想、相邻顶点可区别边着色猜想、相邻顶点可区别全着色猜想、极大平面图唯一4-可着色猜想、具有4 种约束条件的相邻顶点可区别全着色猜想,还有确定Ramsey 数等未解决的问题。
⑤解决或破译NBSTAP 要涉及密码长度、密码元素、拓扑结构这3 个基本要素。已知,没有统一的技术来度量密码强度。当密码元素是数字时,解决或破译NBSTAP 的工作就要在代数(集合论、群)和拓扑结构这2 个不同类型的领域来回交叉碰撞、组合,上面的①、②、③和④分析均涉指数级计算。密码长度成为NBSTAP 的解决或破译的方向问题,例如,一个作为公钥的数字串:

仅仅是图4 中“田”字图L(私钥)的一个2-维编码[10],这个具有9 个顶点的Topsnut-图形编码是图论中优美标号与奇优美标号的混合体,由Topcode-矩阵T(L)很容易写出数字串s(97)。如果猜测公钥s(97)是某些图的度序列(私钥),那么,破译工作将走向死胡同。在文献[11]中,Sheppard 证明:“n个顶点的优美树承认n!/2 个不同的优美标号”。由斯特林公式,说明确定优美树的优美标号是指数级工作,那么,确定树的n-维编码(n≥2)的复杂度也是指数级的。

Fig.4 Hanzi-graphical password L and its own Topcode-matrix T(L)图4 汉字图L 的图形编码及其Topcode-矩阵T(L)
⑥在Topsnut-图形编码中,假设有k种类型的顶点和l种类型的边,m个用来染图的顶点和边的颜色。一个(p,q)-图G承认n(G)种类型的着色,对每种类型的着色ε∈[1,n(G)],图G承认ο(G,ε)个不同的ε-型着色。令Svo(G,p,q)是由(p,q)-图G得到的Topsnut-图形编码集合的元素个数,则有:

取G是(p,p-1)-树,n(G)=ο(G,ε)=1,以及m=k=l,得到Svo(G,p,p-1)=22m(2p-1)。Deo 等人在文献[12]中报道:“不超过29 个顶点的树皆为优美树”。已知具有29个顶点的树共有5 469 566 585棵。当m=2 时,一棵具有29 个白色和黑色顶点的优美树可以产生2228个Topsnut-图形编码。因为5 469 566 585 ≥232,具有29个顶点的优美树可以产生2260个Topsnut-图形编码。
综上分析:由度序列和各种矩阵十分容易地写出数字串,但是由数字串导出图形编码却是困难的,故NBSTAP 具有不可逆性;基于NBSTAP 的格密码体制的体制安全性基于NP-Hard 等困难问题和各种指数级计算;图的相邻矩阵和Topsnut-矩阵同态、Topcode-矩阵、度序列之间、图之间也存在各种同态关系[13-19]。据此断定:基于NBSTAP 的图格能够抗量子计算。
1.3 基本定义、术语和记号
本文采用标准的图论术语和记号,其他没有介绍的概念、术语均可在文献[9,20]中找到。记号[a,b](a 定义设连通(p,q)-图G承认一个全着色f:V(G)⋃E(G)→[1,M](M≥2q),且有某对顶点x,y∈V(G)满足f(x)=f(y)。有以下约束条件: (1)每条边uv∈E(G)的着色为f(uv)=|f(u)-f(v)|; (2)边着色集f(E(G))=[1,q]; (3)顶点着色集f(V(G))⊆[1,q+1]; (4)边着色集f(E(G))=[1,2q-1]ο; (5)顶点着色集f(V(G))⊆[1,2q]; (6)G是偶图,顶点集V(G)=X⋃Y且X⋂Y=∅,使得每条边uv∈E(G)满足u∈X和v∈Y,全着色f满足maxf(X) 如果条件(1)和(2)成立,称f为准优美全着色;如果条件(1)、(2)和(3)成立,称f为优美全着色;如果条件(1)、(2)和(6)成立,则称f为集有序准优美全着色;如果条件(1)、(2)、(3)和(6)成立,则称f为集有序优美全着色。 此外,若条件(1)和(4)成立,则称f为准奇优美全着色;若条件(1)、(4)和(5)成立,则称f为奇优美全着色;若条件(1)、(4)和(6)成立,则称f为集有序准奇优美全着色;若条件(1)、(4)、(5)和(6)成立,则称f为集有序奇优美全着色。 注释1(1)定义导出一个参数:连通(p,q)-图G承认一个优美全着色h,若|h(V(G))|≤|f(V(G))|对图G的任何一个(奇)优美全着色f成立,则记vgtc(G)=|h(V(T))|=minf{|f(V(T))|},称为连通(p,q)-图G的(奇)优美全着色数。一些实验表明,计算优美全着色数vgtc(G)的精确值是不容易的,因为它和图的正常全着色有关联。 (2)如果(准、奇)优美全着色f是正常全着色,必有f(v)≠f(uv)=|f(u)-f(v)|,2f(v)≠f(u),或者f(u)≠f(uv)=|f(u)-f(v)|,2f(u)≠f(v)。一般来说,(准、奇)优美全着色f和自己的对偶着色不一定是正常全着色(见图5 中的例子)。如果(奇)优美全着色也是正常全着色,则称它为(奇)优美正常全着色。类似地可以定义准(奇)优美正常全着色、集有序准(奇)优美正常全着色、集有序(奇)优美正常全着色。 对偶优美全着色的例子在图5 中给出,其中:(1)和(2)互为对偶优美全着色;(3)和(4)互为对偶优美全着色;(1)和(3)是优美正常全着色;但是(2)和(4)不是优美正常全着色。 (3)承认优美全着色的图可以导出承认优美标号(即对任何x,y∈V(G),总有f(x)≠f(y))的图。因此说,定义中的各种优美全着色是普通全着色与优美标号的结合物。与全着色相关的数学问题是著名的全着色猜想(total coloring conjecture),与优美标号相关的数学问题是著名的优美树猜想(graceful tree conjecture),如果每一棵树是优美树,则可以证明Ringel-Kotzig 猜想等[9,20]。 由一个图基和一组图运算以及图集合产生的集合叫作图格,由一个着色图基和一组图运算以及着色图集合产生的集合叫作着色图格,下面给出建立图格和着色图格要用到的几个算法。 引理1每棵树承认一个准优美全着色。 证明取走树T的一条最长路上的一片叶子w,得到树T-w。按照归纳法,树T-w承认一个准优美全着色f,使得树T-w的边着色集合为f(E(T-w))=[1,|E(T)|-1]。设叶子w在树T中与u相邻,定义树T的一个准优美全着色g为: 得到树T的边着色集为g(E(T))=[1,|E(T)|]。证毕。 定理1设基由n个顶点不交的连通偶图H1,H2,…,Hn(n≥2)构成,ek=|E(Hk)|,且e1≥e2≥…≥en。如果每个连通图Hk承认一个集有序优美全着色,则存在边集E*,使得连通边连接图承认一个集有序优美全着色。 证明对整数k∈[1,n],设(Xk,Yk)为基中连通偶图Hk的顶点集二部划分,其中和ak+bk=|V(Hk)|=nk,且连通偶图Hk具有ek=|E(Hk)|条边。根据本引理的假设,连通偶图Hk承认一个集有序优美全着色fk。定义说明着色fk满足maxfk(Xk) Fig.5 Examples for dually graceful total colorings图5 对偶优美全着色的例子 使得图Hk的边着色集为: 上面的推导导致: 添加满足式(5)的边x1,iy2,j或边y1,sx2,i,使得这些边形成一个集合其边数目为构造连通图根据定义,连通图G1承认g1为它的一个集有序优美全着色。 现在考虑图G1和图H3,由于e1≥e2≥e3,按照上面的证明,可以得到边集合,使得边数目用边集合的边构造连通图且连通图G2承认一个集有序优美全着色g2。如此进行下去,数学归纳法证得本引理。 公钥密码体制在现代密码学中占有重要的地位,它由公钥和私钥这两个密钥构成,公钥用于加密或签名的验证,私钥用于解密或签名。基于公钥密码体制,下面对作为公钥的n个顶点连通偶图F,找到顶点不交的连通偶图H1,H2,…,Hn(n≥2) 作为私钥,构成新的连通偶图来完成网络安全的加密、解密或验证。下面给出图的无公共邻点的顶点重合运算“⊙”的定义。设图G与图H没有公共顶点,将图G的一个顶点x与图H的一个顶点u重合成一个顶点x⊙u,所得到的图记为G⊙H。设有图G的2 个顶点x与顶点y,如果2 个顶点的邻点集合满足N(x)⋂N(y)=∅,则将顶点x与顶点y重合成一个顶点x⊙y,所得到的图记为G(x⊙y),称得到图G(x⊙y)的过程为无公共邻点的顶点重合运算。 定理2如果基中的每个图Hk是连通偶图且承认一个集有序优美全着色,n个顶点的连通偶图F承认一个集有序优美全着色,则F-图是连通偶图,且承认一个集有序优美全着色。 证明设连通偶图F的n个顶点为x1,x2,…,xn,且图F承认一个集有序优美全着色h,记图F的边数目为eF=|E(F)|。设偶图F的顶点集二部划分为(X,Y),其中X={x1,x2,…,xs},Y={xs+1,xs+2,…,xn},根据集有序优美全着色的定义,有maxh(X) 下面来定义图F的另一个全着色g。令g(xi)=h(xi)(i∈[1,s]),g(xj)=h(xj)+A+B(j∈[s+1,n])。由于图F的边xixj的着色为g(xixj)=g(xj)-g(xi)=h(xj)+A+Bh(xi)=A+B+h(xixj),图F的边着色集为g(E(F))=[1+A+B,eF+A+B]。现在给基中的每个图Hk用全着色g重新着色。对每个k∈[1,n],下面将图F的顶点xk与连通偶图Hk的某个顶点重合成一个顶点,所得到的连通图记为 从而,图Hs-1的边着色集为: 对连通偶图Hk(k∈[1,s-1]),因为图Hk的顶点xk,1和图F的顶点xk被重合成一个顶点xk,1⊙xk,则将顶点xs-1,1重新着色为g(xk,1)=g(xk)=h(xk)=fk(xk,1)+h(xk)-1;图Hk的其他顶点重新着色为g(xk,i)=fk(xk,i)+h(xk)-1(i∈[1,bk]),g(yk,j)=fk(yk,j)+B+h(xk)-1+I(s-k)(j∈[1,dk]),将图Hk的每条边xk,iyk,j∈E(Hk)重新着色为g(xk,iyk,j)=g(yk,j)-g(xk,i)=B+fk(xk,iyk,j)+I(s-k),上面的顶点和边的着色导出图Hk的边着色集g(E(Hk))=[B+1+I(s-k),B+I(s-k+1)]。图Hk的顶点着色最大值为max{g(w): 综合上述对连通偶F-图的全着色g的证明,知道连通偶F-图G的顶点着色集为g(V(G))⊆[1,A+B+eF+1]=[1,|E(G)|+1],它的边着色集为g(E(G))=[1,A+B+eF]=[1,|E(G)|],故全着色g是连通偶F-图G的一个集有序优美全着色。定理得证。 使得图格(6)中的每一个图是连通边连接图,且承认一个集有序优美全着色,从而证明了着色图格L(E*⊕H)对集有序优美全着色的封闭性。 定理2 的结论导出下面的F-图格: 其中,F*(n)是具有n个顶点的连通偶图之集,F*(n)中的每个连通偶图承认一个集有序优美全着色。一般情形下,有下面的着色图格: 其中,S*是全体承认集有序优美全着色的连通偶图之集。 图6 给出一棵毛毛虫树T,去掉它的所有叶子,剩余的图是一条路P8=u1u20u4u19u8u16u9u15,这条路叫毛毛虫树T的脊椎路。毛毛虫树T的直径是9,它的顶点u1有4 片叶子,顶点u20有2 片叶子,顶点u4没有叶子,顶点u19有3 片叶子,顶点u8有2 片叶子,顶点u16和顶点u9没有叶子,顶点u15有5 片叶子。 Fig.6 Topological vector Vec(T)=(4,2,0,3,2,0,0,5) of a colored caterpillar T图6 一棵着色毛毛虫树T 的拓扑向量Vec(T)=(4,2,0,3,2,0,0,5) 下面建立图格与传统格之间的一个联系。对i∈[1,n](n≥2),每棵毛毛虫树Hi具有脊椎路Pi,n=xi,1xi,2…xi,n,路Pi,n上的每个顶点xi,k有自己的叶子集合ℓ(xi,k)={yi,k,j:j∈[1,bi,k]}(k∈[1,n])。定义毛毛虫树Hi的拓扑向量(topological vector)为Vec(Hi)=(ci,1,ci,2,…,ci,n),其中ci,k=|ℓ(xi,k)|是顶点xi,k相邻的叶子数目。图6 给出一棵毛毛虫树T的拓扑向量Vec(T)=(4,2,0,3,2,0,0,5)毛毛虫树基(caterpillar base)。 Hcater=(H1,H2,…,Hm)=是由m棵顶点互不相交的毛毛虫树H1,H2,…,Hm构成。相应地,得到毛毛虫树基的拓扑向量基(topological vector base)Vec(H)=(Vec(H1),Vec(H2),…,Vec(Hm)),当拓扑向量基Vec(H)中的m个向量是线性无关时,就得到下面的一个非负整数传统格。 因非负整数传统格L(Z0Vec(H))中的仍然是一个拓扑向量,将它对应的毛毛虫树记为称集合: G(L(Z0Vec(H)))={Ca:Vec(Ca)∈L(Z0Vec(H))}为格L(Z0Vec(H))的伴随毛毛虫图格。 注释2关于集有序优美全着色图格,有如下的问题: (2)考虑优美全着色图格中的极值问题,如:最小直径、最多边数、最长圈、是否欧拉图等极值图的问题。 (3)求引理1 中具有最多边数的E*的图G= 本文主要运用定义中的优美全着色建立了具有集有序优美全着色的边连接图格、F-图格等。由于证明技术相似,本文没有对定义中的奇优美全着色进行相应的图格建立及理论研究。一般地,一个图格是建立在某些图的运算和顶点不交的连通着色图构成的图格基。本文研究了图格基在边连接运算、顶点重合运算下的着色保持性、封闭性,使得边连接图格、F-图格都具有着色保持性和封闭性。这里须指出,用承认全着色的图建立的图格具有两个基本特性:拓扑结构、数学约束(拓扑编码)。数字串拓扑认证问题的不可逆性正是依据拓扑结构的同构是NPhard 以及数字串分解的无多项式算法。确定一个图承认一个集有序优美全着色是困难的,即使是树图这类十分简单的图。加深对承认集有序优美全着色连通偶图的研究是十分有意义的。 本文给出了毛毛虫树的拓扑向量概念,建立了以毛毛虫树基为格基的非负整数传统格,从而得到图格与传统格之间的联系,试图将传统格的某些问题转化为图格中的问题,为图论和组合带来新的研究对象和新问题,同时也为格理论增添新分支或新方法[13]。 图格是多种学科融合的产物,图格中的图是用矩阵存储、运行在计算机中的,主要理论技术来自于离散数学、数论、代数学等学科[13-19]。已知不存在解决某些格困难问题的多项式量子算法[1],加之数字串拓扑认证问题是不可逆的,以及图格含有大量的计算困难问题,使得基于数字串拓扑认证问题的图格具有抗超大计算机和量子计算机计算的功能。期望它能够成为密码领域的工具之一,得到数学领域、计算机科学领域、信息安全领域、动态网络的可行、有效的应用[21-22]。致力于汉字编码在实际应用的推广,力图实现使用汉字的人们直接说、写汉字就产生数十位、百位、千位的数字密码,在量子计算机时代大有用场[23-24]。2 优美全着色下的着色图格
2.1 具有优美全着色的图






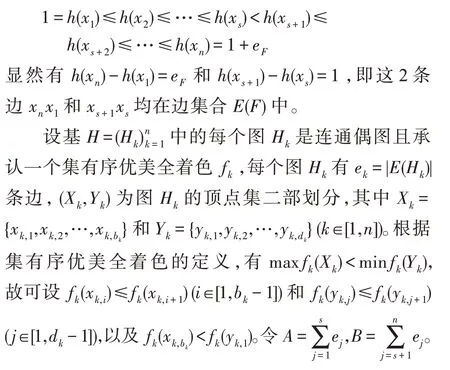


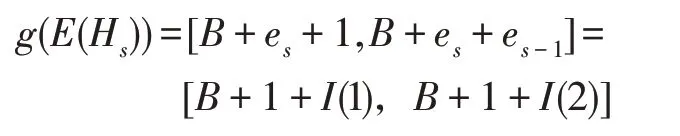
2.2 基于优美全着色的着色图格


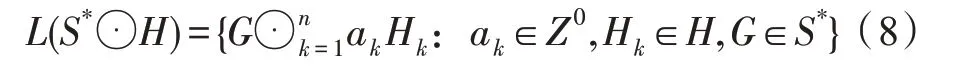

2.3 传统格和图格的联系





3 总结与展望

