基于数据增广训练的深度神经网络方法压制地震多次波

王坤喜, 胡天跃*， 刘小舟， 王尚旭， 魏建新

1 北京大学地球与空间科学学院， 北京 100871 2 中国石油大学(北京)油气资源与探测国家重点实验室， 北京 102249

0 引言

多次波是指在地下界面或者地表反射次数大于一次的同相轴，容易使目的层反射波振幅、频率和相位发生畸变(张广利等，2016; 匡伟康等，2018).由于常规地震数据处理流程大都基于一次波波场，多次波的存在会严重影响速度分析、地震偏移、层析成像，从而误导地震资料的解释，因此多次波一般被看作噪声予以压制消除(胡高伟等，2019; 魏峥嵘等，2020).目前，多次波的压制方法主要有两大类：滤波法和基于波动理论的方法.

滤波法主要利用一次波和多次波在时间和空间特征上存在的差异，通过不同的变换方法压制多次波.预测反褶积是最早被用于多次波压制的方法(Porsani and Ursin, 2007).但是预测反褶积方法只适合压制浅海短周期多次波，且对有效波损伤较大；另一种方法是时差区分法.利用一次波和多次波的动校正速度差异，在完成动校正的共中心点道集上，将已经校平的同相轴归为一次波，没有校平的同相轴归为多次波.常用方法有聚束滤波法(胡天跃等，2000)和Radon域滤波法(石颖和王维红，2012).但是当一次波和多次波具有相同动校正速度或者地下地层横向变化较大时，会减弱此类方法的分离效果.

基于波动理论的方法利用多次波产生机理来预测和压制多次波.根据是否需要提前给出先验假设，该大类方法可以分为模型驱动法和数据驱动法.模型驱动法根据波场的动力学或者运动学特征模拟出多次波，如波场外推法(Wiggins and Wendell, 1988)和自适应变步长波场延拓(匡伟康等，2020).数据驱动法不需要提前知道完整的地层先验信息，适用于复杂的地下结构，包括逆散射级数法(Weglein et al., 1997; 李翔和胡天跃，2009)、反馈迭代法(Verschuur et al., 1992)和虚同相轴法(Ikelle, 2006; Liu et al., 2018b; 吴静等，2013; 刘嘉辉等，2018)等.逆散射级数法要求常速度背景，以保证方法的收敛性，并且要求满足垂直走时单调性假设条件，计算量大，因此影响了实际的使用效果；反馈迭代法和虚同相轴法都要求数据规则化，但是实际采集数据往往因为炮数和道集数不能满足要求而需要进一步对数据插值重构，影响了处理效果.另外，这两类方法都严重依赖匹配算法，如能量最小原理法(Verschuur and Berkhout, 1997)、1范数最小单道匹配法(Guitton and Verschuur, 2004)、多道卷积信号盲分离匹配法(李钟晓等，2012)和模式学习匹配法(Jiang et al., 2020; Li, 2020)等，匹配算法选取的好坏也决定了多次波压制效果.

最近，深度学习作为机器学习领域的一个重要研究方向(Hinton et al., 2006)，在图像处理、自然语言处理、语音识别等领域取得了突破性进展，得到了广泛关注.深度学习方法基于数据驱动，不需要在模型的构建中加入先验知识和人工提取数据特征，能够通过组合低层特征形成更加抽象的高层特征来表示属性类别或特征，从而更好的发现数据的有效特征表示.深度学习方法具有较强的泛化能力，在部分领域取得了比传统方法更加优异的效果.典型的深度学习结构包括:自动编码机(Hinton and Zemel, 1994)、卷积神经网络(LeCun et al., 1998)、循环神经网络(Hochreiter and Schmidhuber, 1997)、深度信念网络(Hinton et al., 2006)、生成对抗网络(Goodfellow, 2016)等.现在，深度学习的应用也成为勘探地球物理学研究的一个活跃领域(赵改善, 2019)，学者们提出了一些基于深度神经网络的方法.Zheng等(2014)在叠前合成地震记录中引入深度学习方法进行了断层识别试验.Huang等(2017)利用卷积神经网络模型在断层检测方面取得进展.Mosser等(2018)使用深层生成神经网络进行地震速度反演建模.Wu等(2019)提出利用人工合成地震数据训练卷积神经网络，并用于实际地震数据中以完成断层自动识别.Das等(2018)提出了一种基于卷积神经网络的波阻抗反演方法，该方法对生成样本进行了准确预测.Liu等(2018a)提出了一种基于数据增广的U-net地震随机噪声压制方法，使用人工合成数据集Pluto中的少量数据进行增广生成有标签数据集来训练网络，在Sigsbee数据集上测试并取得了良好的去噪效果，该方法是对卷积神经网络泛化性的有效探索.Zu等(2020)采用包含卷积和反卷积的深度神经网络，利用混叠数据和真实数据组成的数据块进行学习，采用迭代分离的方法对共检波点域和共偏移距域的混叠数据进行了分离.在多次波消除领域，Siahkoohi等(2019)首先使用SRME(Surface-Related Multiple Elimination)法和EPSI(Estimation of Primaries by Sparse Inversion)法对原始数据进行了预处理，接着用原始数据和预处理得到的一次波数据训练生成对抗网络，最后利用训练好的神经网络压制多次波.Li和Gao(2020)使用卷积神经网络提取预测多次波的多特征数据，并将特征数据用于多次波的匹配中，能够平衡多次波的去除与一次波的保留.

本文设计具有卷积编码和卷积解码过程的深度神经网络结构，使用训练好的神经网络参数，卷积编码部分能够提取地震数据中的一次波信号特征，卷积解码部分能够使用编码部分提取的一次波特征来重构消除了多次波和随机噪声的一次波.由于较少的训练集容易造成神经网络过拟合且实际地震数据中包含较多随机噪声，我们在训练集的输入数据中加入不同强度的随机噪声并通过旋转得到增广数据集从而提高深度神经网络的抗噪能力和泛化性.为了提升深度神经网络跨工区压制多次波的能力并节省训练时间，本文引入迁移学习进一步提升深度神经网络的泛化性能.通过两个简单模型与Sigsbee2B模型三套模拟数据例子和一套崎岖海底地震物理模型模拟数据的应用实例证明本文提出的基于数据增广训练的深度神经网络方法在一次波重构和多次波压制中的有效性、稳定性和良好泛化性.

1 方法

1.1 深度神经网络结构

卷积层可以直接对二维数据进行处理，具有局部感知和参数共享两个特点，每个神经元不需要感知数据中的全部像素，只对局部数据进行感知，然后在更高层将这些局部的信息进行合并，从而得到数据的全部表征信息.为了充分利用二维地震数据在空间上的连续性特征，避免出现难以训练和过拟合的问题(Wu et al., 2019)，本文的神经网络框架主要使用卷积层来学习数据特征，其结构如图1所示.该深度神经网络类似于U-net网络，分为卷积编码器和卷积解码器两个部分，属于监督学习.在卷积编码过程中，9个卷积层和4个下采样层能够抓住地震数据的时间和空间位置关系，学习训练集中的一次波表达特征.在卷积解码过程中，13个卷积层和4个上采样层将包含一次波信号的低维特征映射回高维空间，重构压制了多次波后的一次波地震数据.同时，神经网络中的特征融合(Concat)将卷积编码过程得到的特征与卷积解码得到的数据进行了融合，可以保留更多高层特征图信息，获得更准确的地震时间与空间相干特征，达到更好的多次波识别和分离效果.为了提高深度神经网络的泛化性能，我们在第9和第10层使用Dropout(Srivastava et al., 2014)随机丢弃50 %的神经单元，提升深度神经网络的泛化能力.

1.2 常规训练法

在图1的深度神经网络结构中，最左端为输入数据，最右端为输出数据.在训练过程中，输入数据由2个通道的数据组成，第一通道为全波场数据F，第二通道为预测多次波M(Verschuur and Berkhout, 1997).训练过程中的输出数据也称为标签数据，由真实一次波P组成，输入数据与标签数据一起组成训练集数据对{(F,M);P}.在训练过程中，需要将训练集数据对振幅归一化到[-1,1].

图1 深度神经网络结构Fig.1 Structure of the deep neural network

在模型数据或实际数据中，共炮点全波场道集数据记为数据集HF；对应的预测的多次波记为数据集HM、只含一次波的数据记为数据集HP.在深度神经网络训练阶段，数据集HF、HM和HP中相同位置等间隔抽取NUM1个共炮点道集数据，得到输入数据和标签数据，分别记为HFk、HMk和HPk,k=1,2,3,…,NUM1.输入数据HFk、HMk和标签数据HPk一同组合为常规训练数据集对，我们称使用常规训练数据集对来充当训练集对{(F,M);P}并训练深度神经网络的方法为常规训练法.

1.3 数据增广训练法

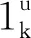
(1)

(2)

当k取值相同时，输入数据都包含相同的全波场和预测多次波，只是随机噪声含量不同，对应的标签数据都包含相同的真实一次波.

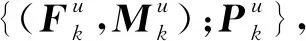
(3)

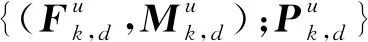
1.4 网络训练

在训练深度神经网络时，每个网络层都包含卷积运算，公式为：

(4)

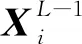
由于卷积运算是线性运算，需要通过激活函数σ处理进行非线性映射：

(5)

在前21个卷积层中，使用的激活函数是ReLU函数(Wu et al., 2019)，该激活函数的单侧抑制作用可以有效保持神经元的稀疏性，其数学表达式为：

(6)

即当输入x小于0时，处于失活状态，当输入x大于0时，处于激活状态.ReLU函数能够避免梯度消失和梯度爆炸问题，且大大简化了反向传播的计算量(Yu et al., 2019).由于在最后一层卷积层中，输出数据值分布范围为[-1,1]，所以这一层的激活函数是双曲正切函数Tanh：

(7)

(8)

其中，N代表训练样本对的数量，本文采用Adam优化算法(Zu et al., 2020)来最小化损失函数.Adam优化算法为不同的参数设计独立的自适应性学习率，通过梯度的一阶矩估计和二阶矩估计的计算来实现(Kingma and Ba, 2014)，能在保持较低内存需求的同时获得很高的计算效率.

2 算例

2.1 第一个简单模型

本文设计的第一个简单模型如图2所示，共7个水平层.有限差分正演得到200个全波场共炮点道集数据和对应的不含表面多次波的真实一次波数据，并通过卷积得到预测多次波.每炮共200道接收.

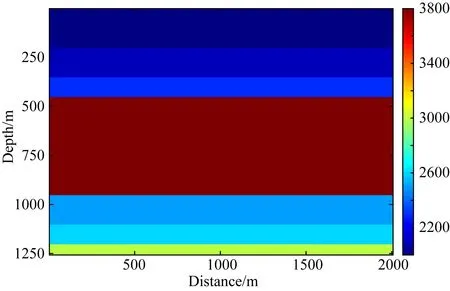
图2 第一个简单速度模型Fig.2 The first simple velocity model

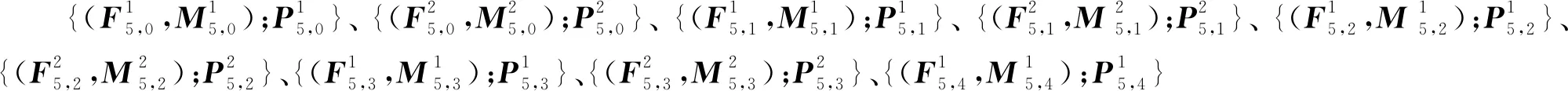
分别将常规训练数据集对和增广训练数据集对送入深度神经网络中进行训练，训练平台为Keras，显卡为GeForce RTX 3090，神经网络的优化算法Adam的初始学习率为1×10-4.式(8)中的损失函数用于计算每轮训练中神经网络得到的估计值和真实值的逼近程度，值越接近，Loss(θ)越小.本次实验训练了400轮(Epoch)，保留每轮训练得到的神经网络参数，并挑选验证集误差最小情况下对应的神经网络参数.常规训练法每轮用时1 s，得到的神经网络参数为θA，得到误差损失函数的迭代曲线如图4a所示，收敛后训练集和验证集的损失值为5.1×10-4和6.9×10-4；数据増广训练法每轮用时39 s，得到的神经网络参数为θB，得到误差损失函数的迭代曲线如图4b所示，收敛后训练集和验证集的损失值为1.3×10-4和1.8×10-4.通过对比常规训练法和数据増广训练法得到的损失曲线，后者得到的训练集和验证集损失值要更小，证明数据増广训练法的训练效果更好.

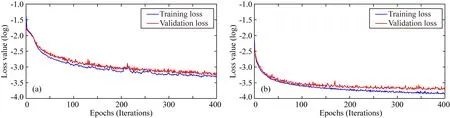
图4 第一个简单模型的训练集和验证集损失曲线(a) 使用常规训数据练集； (b) 使用增广训练数据集.Fig.4 Loss curve of the training set and the validation set for the first simple model(a) Using the general training data set; (b) Using the augmented training data set.

没有参与训练的数据被用来测试深度神经网络的多次波压制效果和抗噪能力.图5a为干净全波场数据.为了测试抗噪能力，图5a中加入不同强度的高斯白噪声和椒盐噪声得到如图5b所示的信噪比(SNR，Signal-to-Noise Ratio)为6.5 dB的带噪全波场数据.图5c为真实一次波，图5d为真实多次波，图中箭头指示一次波和多次波重叠处.图6a为使用SRME法压制干净全波场数据中多次波后得到的一次波结果，该一次波结果与真实一次波之间的差异如图6d所示.图6d显示一次波信号泄漏较严重.一次波和多次波信号重叠时，预测相减法容易造成一次波信号的泄漏.图5b中的一次波和多次波信号都被噪声湮没，使用传统方法压制多次波前都需要消除随机噪声，否则难以取得较好的多次波压制效果.

图5a、b与对应预测多次波分别组合为输入数据后送入参数为θA的深度神经网络中，得到的结果如图6所示.图6b为从干净全波场数据中重构的一次波.图6c为从带噪全波场数据中重构的一次波.可以看出，图6b中多次波都得到压制，一次波重构效果较好，图6c得到的一次波结果中仍然夹带少量随机噪声.真实一次波与常规训练法得到的一次波重构结果(图6b、c)之间的差异分别如图6e、f所示.图6f中可见大量泄漏的一次波信号以及部分未被压制的多次波信号和随机噪声.以上实验证明，参数为θA的深度神经网络不能很好地重构含随机噪声的全波场数据中一次波，常规训练法得到的深度神经网络不具有良好的抗噪稳定性.

图5 第一个简单模型测试数据(a) 干净的全波场数据； (b) 带噪全波场数据； (c) 真实一次波； (d) 真实多次波.Fig.5 Test data of the first simple model(a) Clean full wavefield data; (b) Noisy full wavefield data; (c) True primaries; (d) True multiples.

图6 SRME法和常规训练法得到的分离结果(a) SRME法得到的一次波； (b)(c) 分别为从干净全波场数据、信噪比为6.5 dB的带噪全波场数据中重构的一次波； (d)(e)(f) 分别为真实一次波与(a)(b)(c)之间的差异.Fig.6 Separation results obtained by SRME method and the general training method(a) Primaries obtained by SRME method； (b)(c) are the primaries reconstructed from the clean full wavefield and the noisy full wavefield with a SNR of 6.5 dB； (d)(e)and (f) are the differences between true primaries and (a)(b) and (c), respectively.

使用参数为θB的深度神经网络压制图5a、b中多次波，得到的结果如图7所示.图7a、b都为数据増广训练法重构的一次波，可以发现一次波都得到了完全地识别和重构，没有随机噪声残留.我们将真实一次波与数据増广训练法重构的一次波作差，分别得到如图7c、d所示的重构差异图.从差异图可以发现，重构的一次波信号损失都很小，几乎没有随机噪声和多次波的残留，证明数据増广训练法得到的深度神经网络具有良好的多次波压制效果和抗噪稳定性.

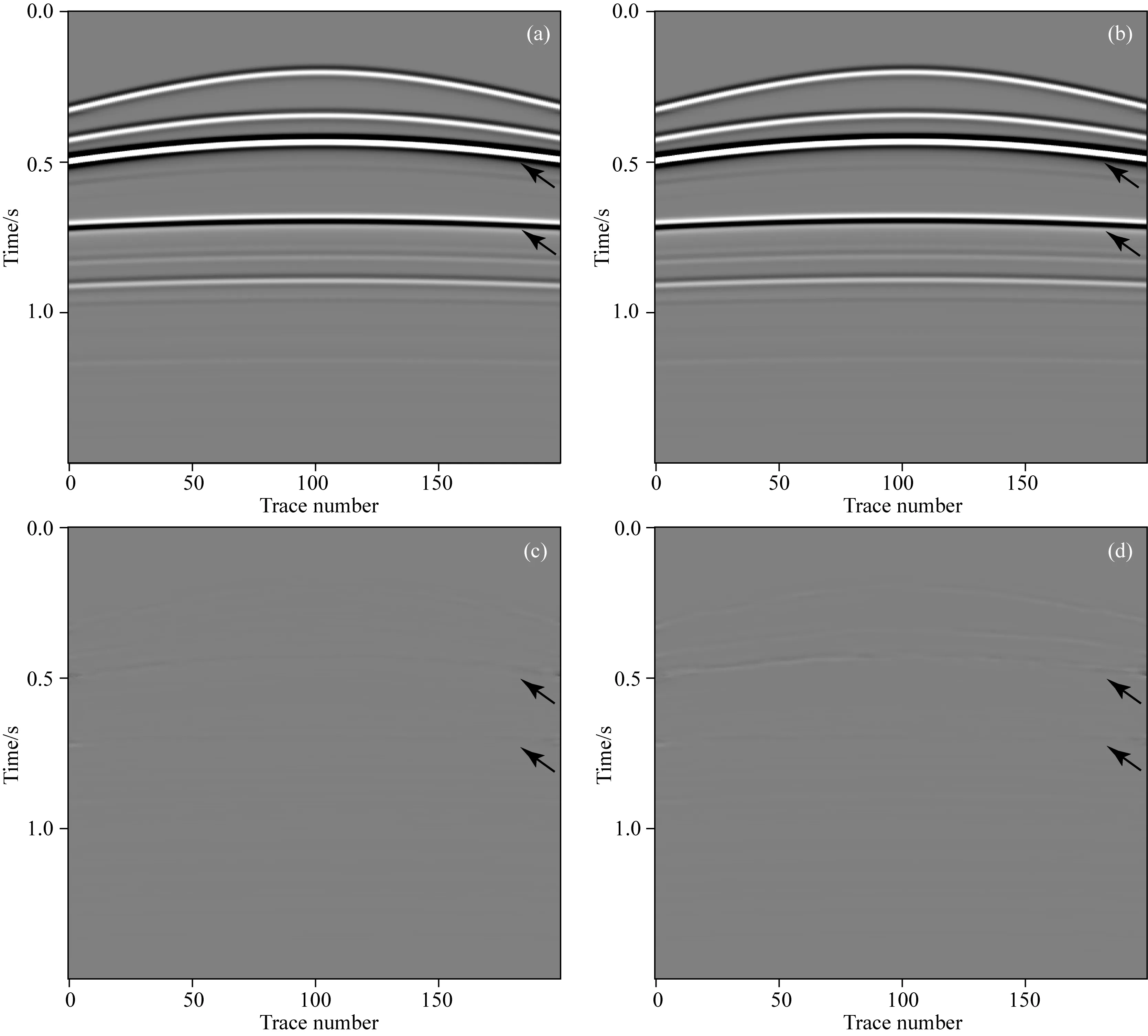
图7 数据増广训练法分离结果(a)(b) 分别为从干净的全波场数据、信噪比为6.5 dB的带噪全波场数据中重构的一次波； (c)(d) 分别为真实一次波与(a)(b)之间的差异.Fig.7 Separation results by the data augmented training method(a)(b) are the primaries reconstructed from the clean full wavefield and the noisy full wavefield with a SNR of 6.5 dB, respectively; (c)(d) are the differences between true primaries and (a)(b), respectively.

为了定量计算深度神经网络的一次波重构和多次波压制效果，本文定义如下一次波重构率：

(9)

式中，Ttrue代表真实一次波数据，Test代表重构的一次波数据.R越高，意味着差异图中泄漏的一次波更少，多次波的压制效果更好.相较于将压制的多次波能量与真实多次波能量简单相除的做法(比如计算多次波压制信噪比)，这个指标更能客观全面地反映一次波重构和多次波压制情况.根据式(9)，SRME法得到的一次波重构率为92.86%.不含噪声的全波场数据、SNR为6.5 dB的带噪全波场数据经过参数为θA深度神经网络处理后得到的一次波重构率分别为98.53%和31.16%，经过参数为θB深度神经网络处理后得到的一次波重构率分别为99.64%和99.42%.可见处理不带噪声全波场数据时，常规训练法和数据増广训练法训练的深度神经网络得到的R都很高，都能很好地重构一次波.但是随着背景噪声的增加，常规训练法训练的深度神经网络增大了一次波泄漏，减弱了多次波的压制效果，导致R减小.相反，数据増广训练法得到的深度神经网络在强背景噪声条件下仍然能够准确重构一次波，有效压制多次波，获得较高的重构率R.以上对比进一步证明常规训练法得到的深度神经网络不适合重构带噪全波场数据中的一次波，数据増广训练法能够提升深度神经网络的抗噪稳定性.

为了理解深度神经网络的工作过程，由图5b与对应预测多次波组成的测试数据被输入参数为θB的深度神经网络中，图8展示网络中部分卷积层输出的特征图，用于可视化中间激活.图8a—f分别为图1中E1、D3、E2、D2、E3和D1卷积层部分通道得到的输出值，且按照通道并排绘制.在卷积编码过程中，如图8a所示，浅层的激活几乎保留了带噪全波场数据中的所有信息；随着层数的加深，如图8c所示的一次波、多次波和随机噪声的特征逐渐分开，激活变得越来越抽象；图8e中大部分特征图是空白，一次波、多次波和随机噪声的特征几乎得到完全分离，稀疏程度最高；在卷积解码过程中，编码过程学习到的如图8e所示的一次波稀疏特征逐渐被解码还原到高维空间，输出值逐渐变稠密，如图8f所示；随着网络深度的增大，如图8d所示，网络逐渐丢掉多次波和随机噪声的特征；在深度神经网络的最深部，如图8b所示，网络内部的学习内容几乎只存在一次波.

图8 可视化结果(a)(b)(c)(d)(e)和(f)分别为深度神经网络结构中E1、D3、E2、D2、E3和D1层激活的部分通道.Fig.8 Visualization results(a)(b)(c)(d)(e) and (f) are the partial channels activated by the E1, D3, E2, D2, E3, and D1 layers in the deep neural network structure, respectively.

2.2 第二个简单模型

本文第二个简单模型如图9所示，用于验证本文设计深度神经网络的泛化能力.速度模型共4个水平层，浅部到深部的速度分别为2500 m·s-1、3500 m·s-1、2500 m·s-1和4000 m·s-1.有限差分正演得到200个共炮点全波场道集数据和对应的不含表面多次波的共炮点地震数据，并通过卷积运算得到预测多次波.每炮共200道接收.

图9 第二个简单水平层速度模型Fig.9 Velocity model of the second simple horizontal strata

在本次试验的训练阶段，我们将图1中部分神经网络层参数锁定并直接使用θB中保存的参数，通过迁移学习提升深度神经网络的泛化能力.等间隔抽取10组数据参与训练.首先利用SRME法预处理全波场数据，并将得到的一次波作为深度神经网络的标签数据.在全波场数据和对应预测多次波中加入11种不同强度的随机噪声，即NUM1=10，NUM2=11，并以30°旋转11次得到增广训练数据集对.最后将获得的增广训练数据集对送入深度神经网络中训练没有锁定的神经网络参数，训练了20轮，每轮用时27 s，并将训练完成时的神经网络参数记为θC.迁移学习得到的损失曲线如图10所示，可以发现训练过程很快趋于收敛.

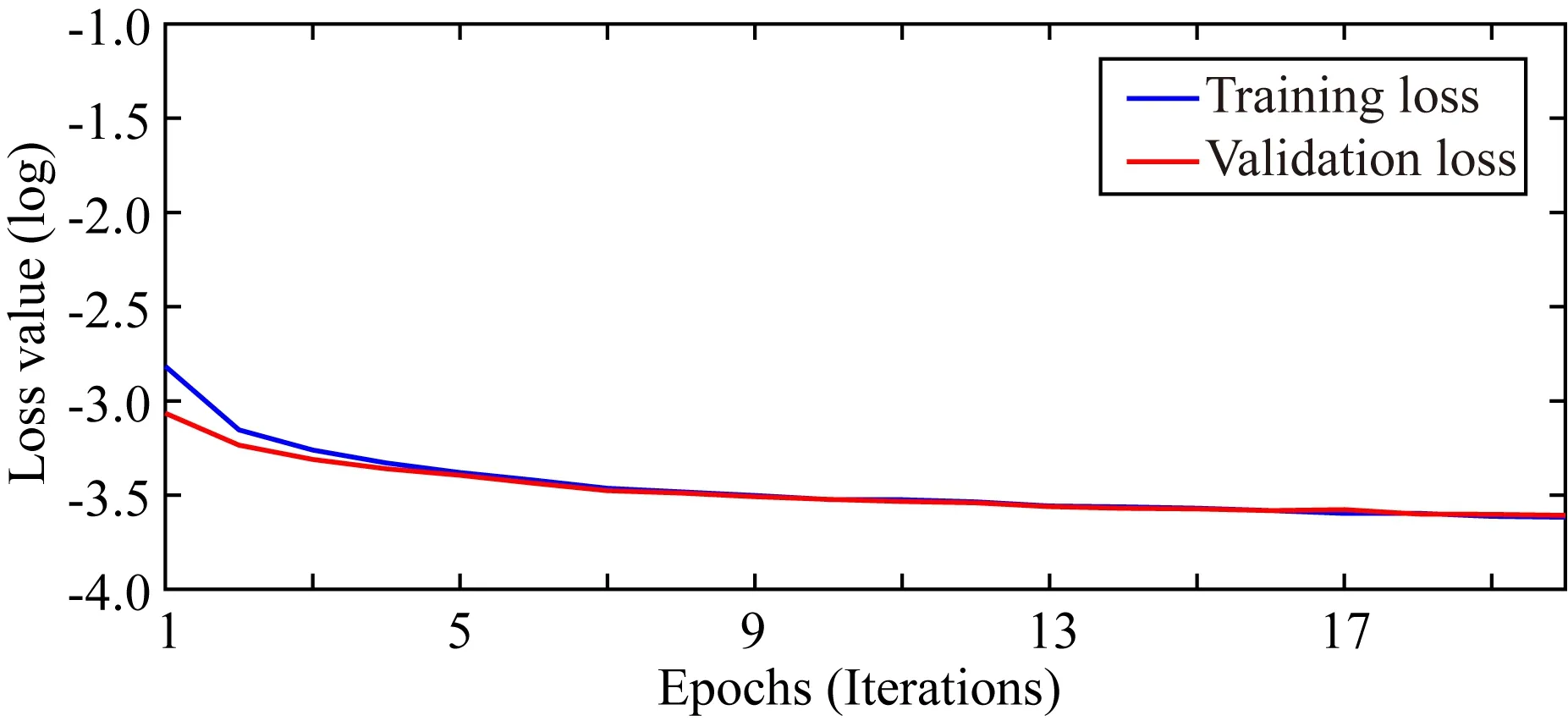
图10 迁移学习训练得到的训练集和验证集损失曲线Fig.10 Loss curve of training set and validation set obtained by training with transfer learning

没有参与迁移学习的数据被用来测试本文方法的多次波压制效果和抗噪能力.图11a为干净的全波场数据，图11b为信噪比为3.5 dB的带噪全波场数据，图11c为真实一次波，图11d为真实多次波.对比可见，图11b中表面多次波特别发育，随机噪声强度大.使用SRME法压制图11a数据得到的结果如图12a所示，一次波重构率R为94.71 %，压制结果与真实一次波之间的差异如图12b所示.从SRME法压制结果中可以发现主要的一次波同相轴得到较好的保护，差异图中可见少量残留的多次波.为了验证本文方法的泛化能力，分别将图11a的全波场数据和图11b的带噪全波场数据输入迁移学习后的深度神经网络中，得到的结果如图13所示.图13a为深度神经网络压制干净全波场数据中多次波得到的结果，一次波重构率R为95.36%，略高于SRME法得到的重构率，证明迁移学习下的本文方法能够有效压制多次波，一次波的重构效果略优于SRME法.迁移学习下重构的一次波与真实一次波之间的差异如图13b所示.从差异图可以发现，本文方法残留的多次波比SRME法残留的多次波更少.本文方法分离信噪比为1.5 dB的带噪全波场数据得到图13c所示的一次波，可以发现强随机噪声得到了完全消除，多次波得到了较好地压制，一次波重构率R为94.59%，该一次波重构率与SRME法和本文方法压制干净全波场数据中多次波得到的重构率相当，进一步说明本文方法具有优越的抗噪稳定性.图13d为真实一次波与图13c之间的差异，该差异图中几乎看不到随机噪声的残留.

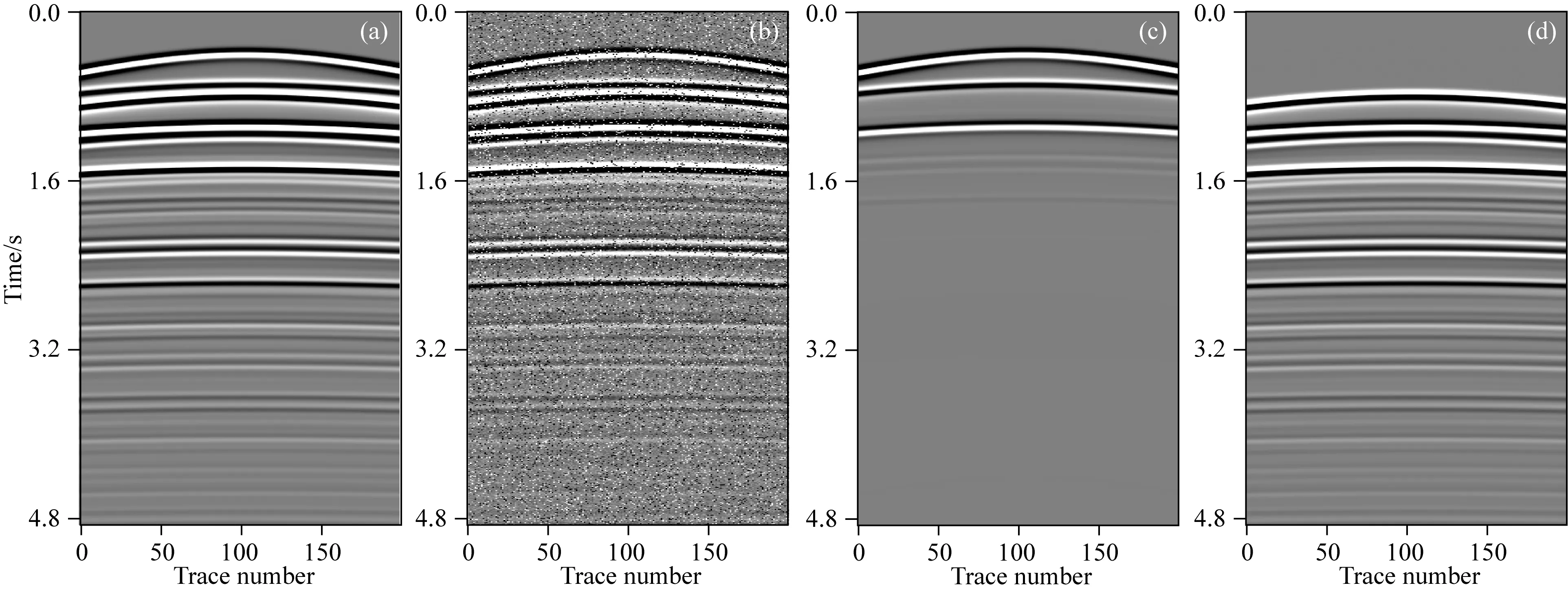
图11 第二个简单模型测试数据(a) 干净的全波场数据； (b) 带噪全波场数据； (c) 真实一次波； (d) 真实多次波.Fig.11 Test data of the second simple model(a) Clean full wavefield data; (b) Noisy full wavefield data; (c) True primaries； (d) True multiples.

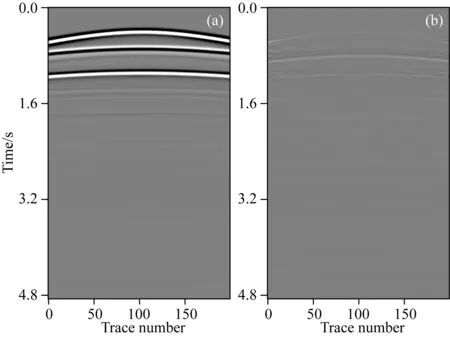
图12 SRME法压制多次波的结果和差异(a) 压制结果； (b) 真实一次波与(a)的差异.Fig.12 Result and difference using SRME method to suppress multiples(a) Suppression result; (b) Difference between the true primaries and (a).

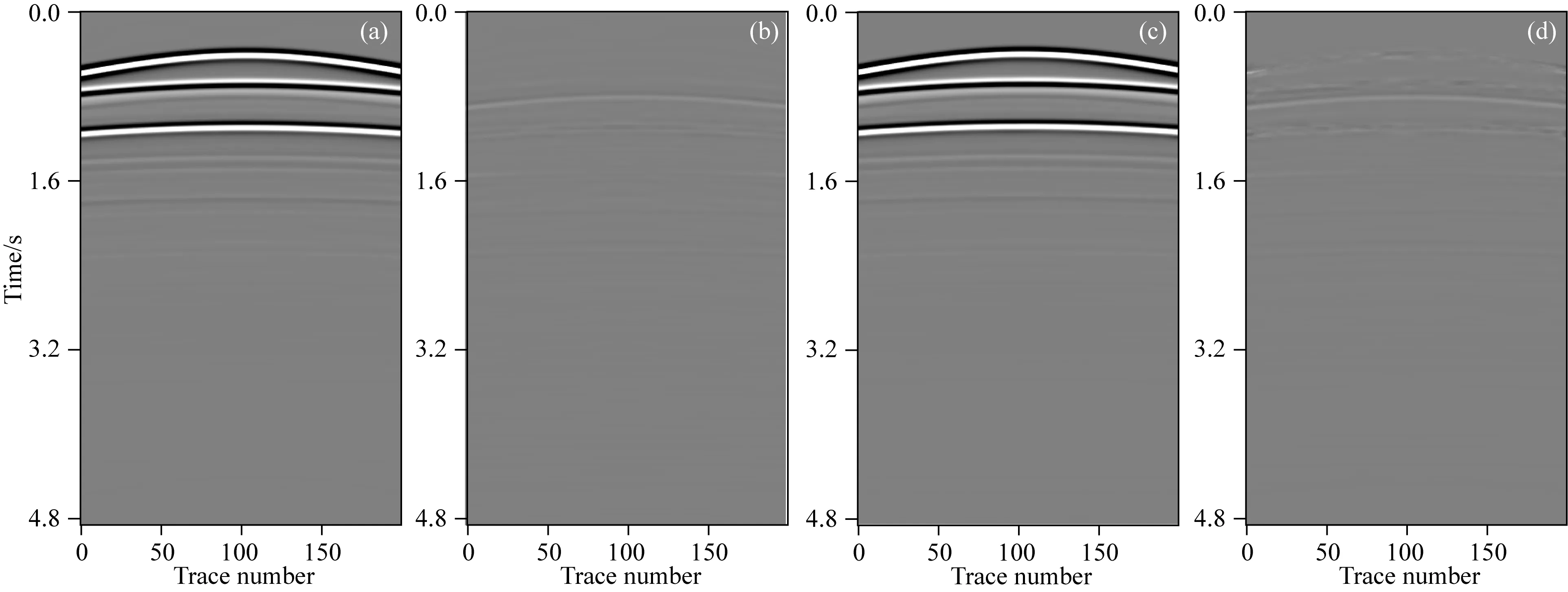
图13 迁移学习下本文方法压制多次波的结果和差异(a) 从干净全波场数据中压制的结果； (b) 真实一次波与(a)的差异； (c) 从带噪全波场数据中压制的结果； (d) 真实一次波与(c)的差异.Fig.13 Results and differences using the proposed method to suppress multiples under transfer learning(a) Result suppressed from clean full wavefield data; (b) Difference between the true primaries and (a)； (c) Result suppressed from the noisy full wavefield data； (d) Difference between the true primaries and (c).

2.3 Sigsbee2B模型

为了进一步验证本文提出的深度神经网络在数据増广训练法下重构一次波和压制表面多次波的能力，本文使用正演的Sigsbee2B模型数据来测试方法效果.Sigsbee2B模型具有很强的水底界面多次波和盐丘顶界面多次波，是石油工业界用于多次波压制方法测试的一个复杂地质模型，速度模型如图14所示.在深度神经网络训练阶段选取60个等间隔激发产生的共炮点道集数据参与训练.为了提高训练集数据量和提升神经网络的抗噪稳定性，根据式(3)在每个输入数据中加入10种不同强度的随机噪声，并以45°旋转7次得到增广训练数据集对.另外，本文选取2个共炮点道集数据加入20种不同强度的随机噪声且进行相同旋转得到増广验证集对.本次深度神经网络参数训练共迭代了400轮(Epoch)，每轮耗时212 s.训练收敛后，神经网络参数记为θD，并用于测试阶段的一次波重构中.

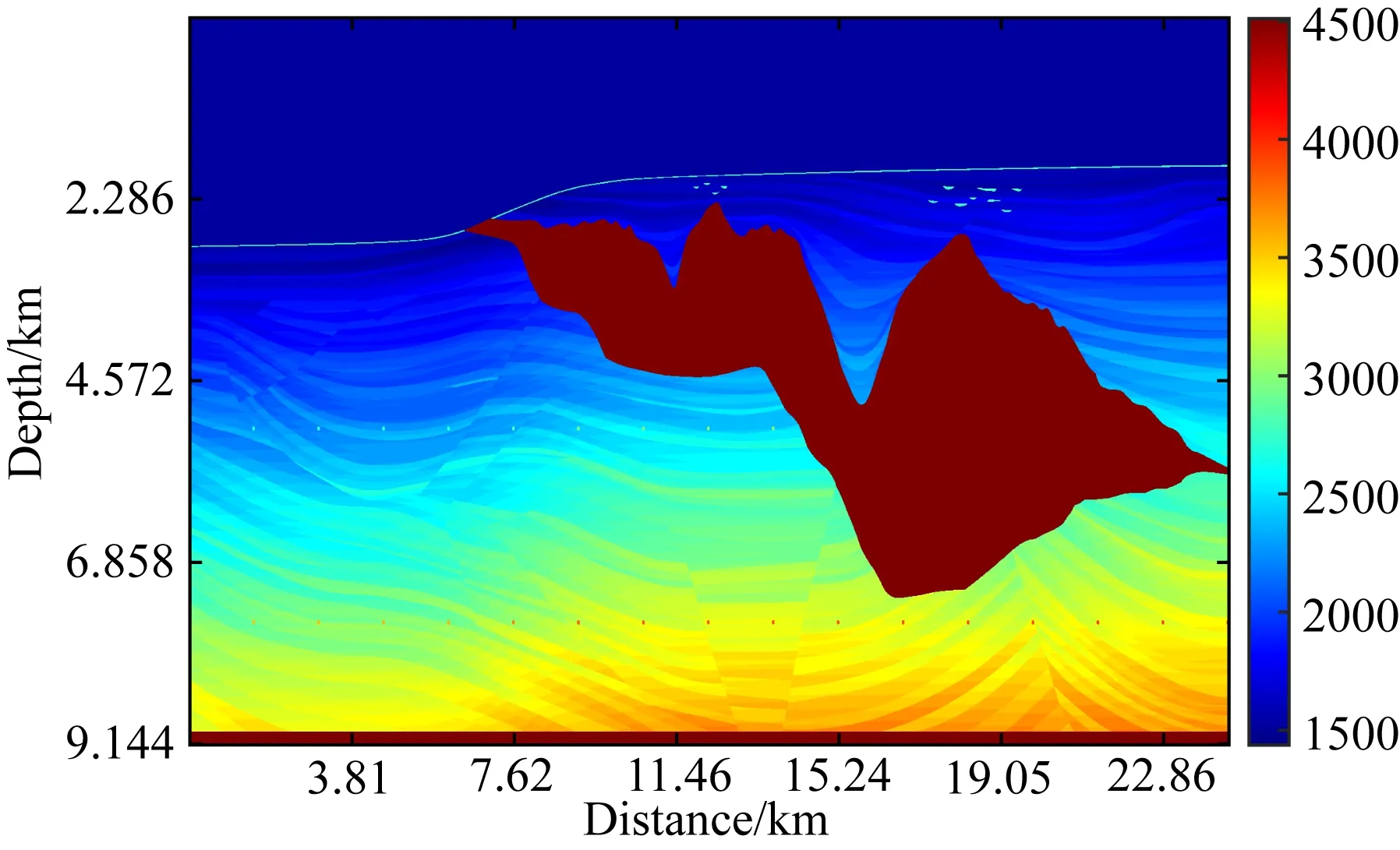
图14 Sigsbee2B速度模型Fig.14 Velocity model of Sigsbee2B

没有参与训练的数据经过振幅归一化后输入参数为θD的深度神经网络中用来测试一次波的重构效果.图15a为测试用的全波场数据，图15b为真实一次波，图15c为真实多次波.一次波主要分布于7.2 s以前的道集记录中，多次波主要分布于5.6 s以后的道集记录中.对比可见，在采集时间为7.2～8.8 s的全波场数据中多次波能量很强，这些多次波严重干扰了一次波信号.

将图15a数据与对应预测多次波输入参数为θD的深度神经网络中，重构的一次波结果如图16a所示，被压制的多次波数据如图16b所示.从结果可以看出，一次波和多次波几乎被完全分离，7.2 s前的一次波都得到良好地重构，8.8 s后的能量较弱的一次波也得到了保护，强振幅多次波信号也几乎被完全压制.为了直观看到一次波重构效果，将图15b的真实一次波与图16a的重构一次波相减得到如图16c所示差异图.从差异图中可以看出，只有少部分一次波信号发生泄漏.根据式(9)定量计算得到一次波重构率为89.63%，一次波得到了良好地重构，多次波压制效果较好.

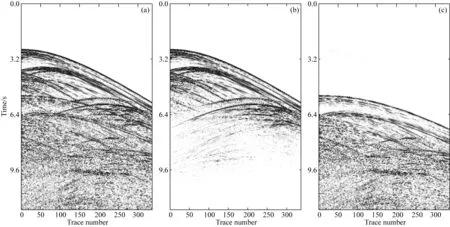
图15 共炮点道集数据(a) 全波场数据； (b) 真实一次波； (c) 真实多次波.Fig.15 Common shot gather data(a) Full wavefield data; (b) True primaries; (c) True multiples.

图16 本文方法分离干净全波场数据的结果和差异(a) 重构的一次波； (b) 被压制的多次波； (c) 真实一次波和(a)的差异.Fig.16 Results and difference from the clean full wavefield data using the proposed method(a) Reconstructed primaries; (b) Suppressed multiples; (c) Difference between true primaries and(a).

进一步使用共零偏移距剖面观察一次波重构和多次波压制的效果.图17a为没有添加高斯白噪声和椒盐噪声的干净全波场共零偏移距剖面，可以在7.6 s附近看到明显的表面多次波.真实一次波共零偏移距剖面如图17b所示.全波场中的多次波被本文方法压制后得到如图17c所示的重构的一次波共零偏移距剖面，可见多次波得到了有效地压制，一次波得到了完全恢复，没有引入其他噪声.真实一次波共零偏移距剖面和重构一次波共零偏移距剖面之间的差异如图17d所示，从剖面差异中可知，只有少量一次波泄漏，深部弱一次波得到了完全地恢复和重构，几乎没有多次波残留.以上结果证明本文方法能够识别并压制多次波，且能有效重构一次波.

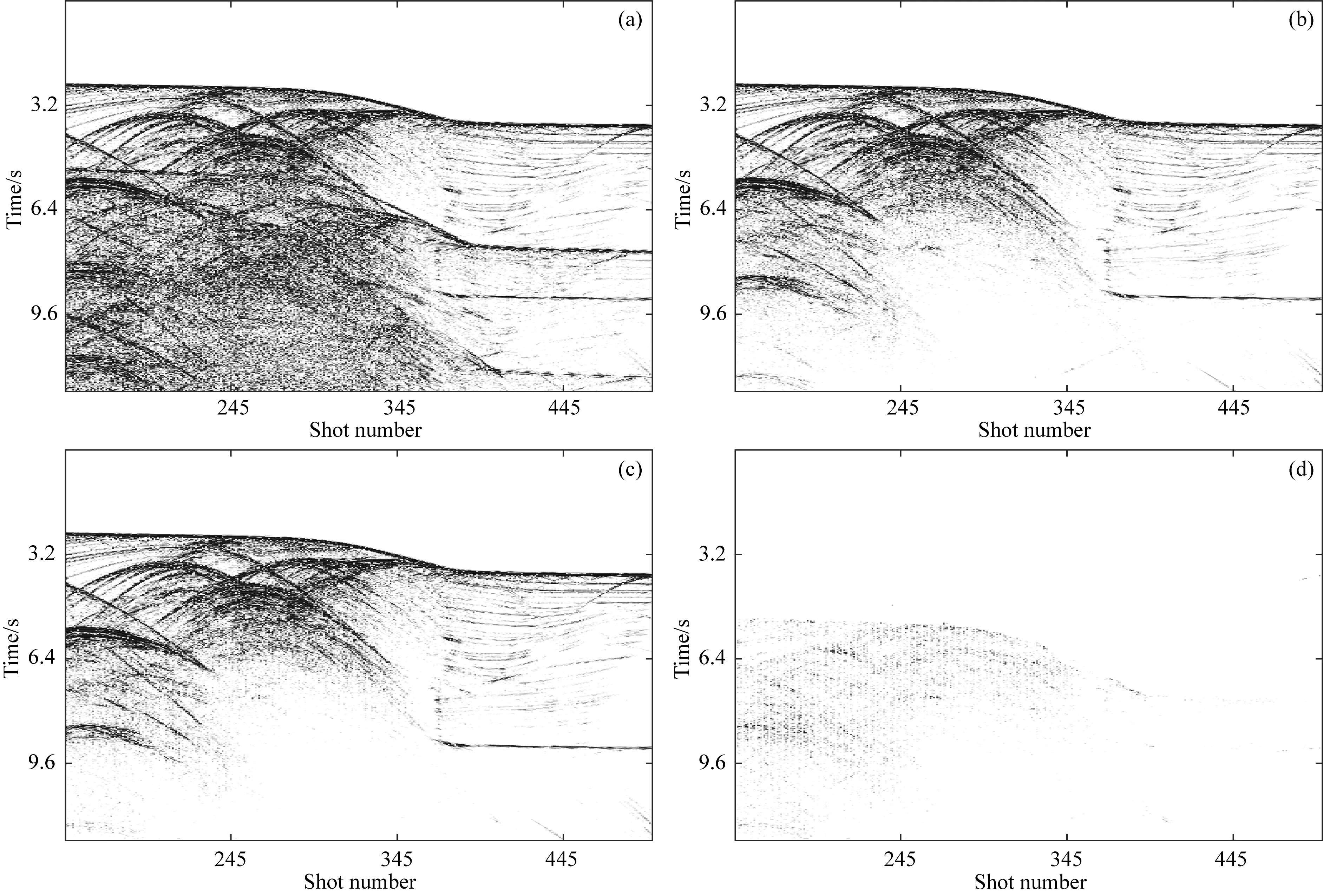
图17 本文方法重构Sigsbee2B模型数据一次波前后的共零偏移距剖面和差异(a) 全波场数据共零偏移距剖面； (b) 真实一次波共零偏移距剖面； (c) 重构的一次波共零偏移距剖面； (d) 图(b)和图(c)的差异.Fig.17 Common zero-offset sections obtained by the proposed method before and after reconstructing the primaries of the Sigsbee2B model data and the corresponding difference(a) Common zero-offset section of the full wavefield data; (b) Common zero-offset section of the true primaries; (c) Common zero-offset section of the reconstructed primaries; (d) Difference between (b) and (c).

由于采集的地震数据中往往包含大量随机噪声，本文在全波场数据中加入随机噪声进一步测试在数据増广训练法下深度神经网络的抗噪能力.在图15a中加入高斯白噪和椒盐噪声后得到如图18a所示信噪比为5 dB的带噪全波场数据，可见随机噪声弥散在整个地震数据中且湮没了部分深部弱信号.经过参数为θD的深度神经网络处理后，本文方法重构的一次波结果如图18b所示.图18b显示一次波信号得到了很好地重构，几乎看不到随机噪声的残留，弱的一次波信号仍然能在强随机噪声和强振幅多次波背景下得到有效恢复和重构.真实一次波与图18b之间的差异如图18c所示，可见泄漏的一次波很少.在记录时间为7.2～8.8 s的全波场数据中，一次波信号很弱且完全被多次波和随机噪声湮没，但在分离结果中几乎被完全重构，证明本文方法能够很好地压制多次波，保护深部弱一次波信号，且没有引入新的噪声.根据式(9)，处理信噪比为5 dB的带噪全波场数据得到的一次波重构率为85.31%，一次波重构率较高，进一步证明本文方法具有较高的抗噪稳定性.

图18 本文方法重构信噪比为5 dB全波场数据中一次波前后的结果和差异(a) 带噪全波场数据； (b) 重构的一次波； (c) 真实一次波和(b)的差异.Fig.18 Primary reconstitution results of the full wavefield data with a SNR of 5 dB before and after using the proposed method and the corresponding difference(a) Noisy full wavefield data; (b) Reconstructed primaries; (c) Difference between true primaries and (b).

使用参数为θD的深度神经网络压制全部带噪全波场数据中多次波和随机噪声后，得到的共零偏移距剖面如图19a所示.一次波得到了很好地重构，没有随机噪声的污染，也没有引入新的噪声，证明使用数据増广训练法得到的深度神经网络具有良好的一次波重构能力和抗噪稳定性.真实一次波共零偏移距剖面与图19a之间的差异如图19b所示.对比分析图17d和图19b可以发现，多次波干扰处都有少量一次波泄漏且泄漏的程度相当，但是深部弱一次波信号都几乎被完全地恢复和重构，证明基于数据増广训练法的深度神经网络从不同噪声背景中重构的一次波效果都很好，具有良好的抗噪稳定性.

图19 本文方法从信噪比为5 dB的含噪全波场数据中重构的一次波共零偏移距剖面和剖面差异(a) 重构的一次波共零偏移距剖面； (b) 真实一次波共零偏移距剖面和(a)的差异.Fig.19 Common zero-offset section of the reconstructed primaries using the proposed method from the noisy full wavefield data with a SNR of 5 dB and the corresponding difference(a) Common zero-offset section of the reconstructed primaries; (b) Difference between the common zero-offset section of the true primaries and (a).

2.4 地震物理模型

以南海某地崎岖海底为原型在实验室按照与野外地质体尺寸比1∶20000设计并制作了物理模型，图20为地震物理模型地层示意图.共激发700炮，每炮288道接收，炮间距为25 m，道间距为12.5 m.本文对其中150个全波场道集数据添加3种不同强度高斯白噪声和椒盐噪声，并以45°旋转7次得到训练的输入数据.使用Radon法对选取的全波场数据进行预处理得到标签数据，每个全波场道集数据处理平均用时82 s.在训练阶段，在参数θD基础上经过迁移学习训练得到神经网络参数θE，每轮用时268 s.

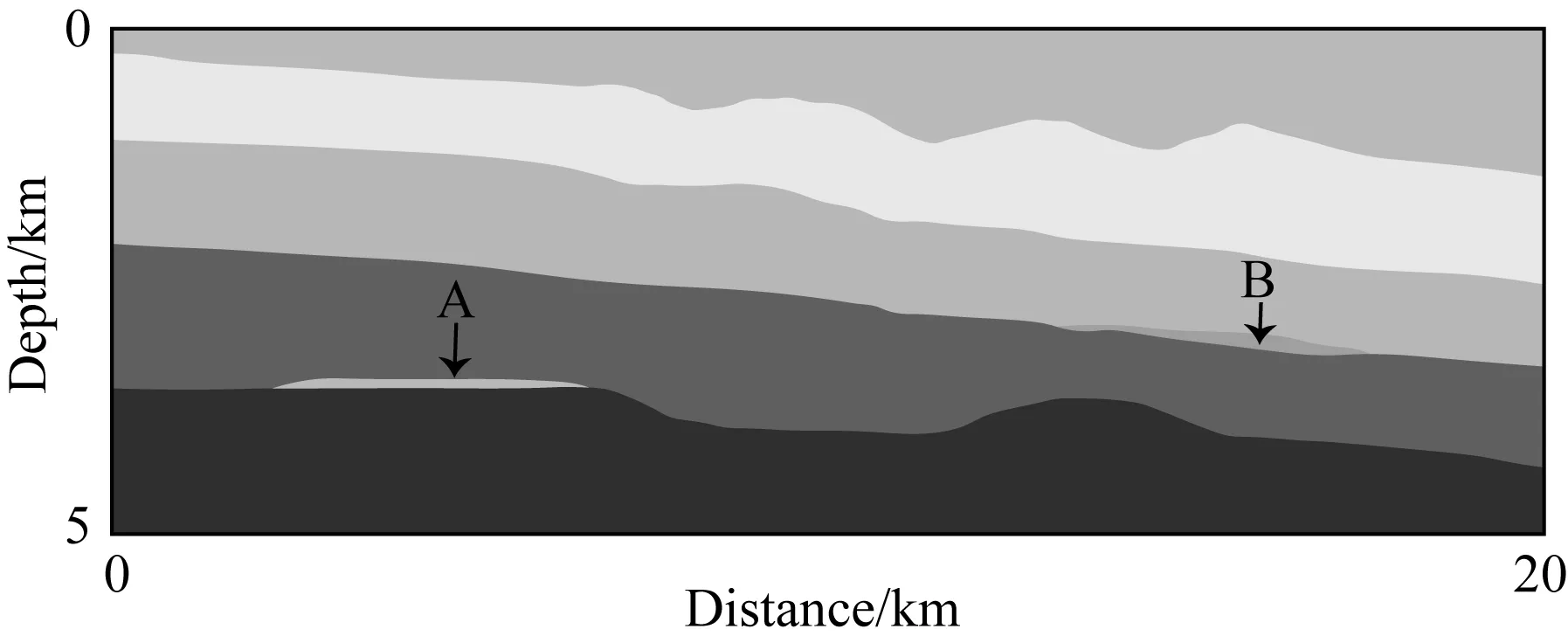
图20 地震物理模型地层其中A代表气层，B代表扇体.Fig.20 Strata schematic diagram of the seismic physical modelA represents the gas layer and B represents the fan body.

图21a为未参与训练的原始全波场数据，其中线性噪声发育，4.8 s后的记录中发育大量多次波，且浅层多次波能量很强.在测试阶段，全部全波场数据都添加高斯白噪声和椒盐噪声得到加噪后全波场数据.图21b为在图21a中添加了高斯白噪声和椒盐噪声后的全波场数据.Radon法压制图21a中多次波得到的结果如图22a所示，参数为θE的深度神经网络压制图21a、b中多次波得到的结果分别如图22b、c所示.对比表明，Radon法得到的结果中残留的多次波较多，如图22a中黑色箭头所示.在本文方法处理的结果中，4.8 s前记录的浅层多次波能量大幅减弱，4.8 s后记录的深层多次波几乎被完全压制，线性噪声、添加的的高斯白噪声和椒盐噪声得到消除.图22中白色箭头处显示本文方法压制原始全波场数据中多次波的效果略好于压制加噪后全波场数据中多次波的效果，但是都优于Radon法的压制效果.图23a为原始全波场数据得到的叠加剖面，表面多次波特别发育，图中黑色实箭头指示强能量多次波.图23b为加噪后全波场数据叠加剖面，随机噪声湮没了部分一次波和多次波.图23c为Radon法压制原始全波场数据中多次波得到的叠加剖面，图23d为本文方法压制原始全波场数据中多次波得到的叠加剖面，图23e为本文方法压制加噪后全波场数据中多次波得到的叠加剖面.图23c—e中的黑色实箭头处多次波都得到了良好地压制，但是图23c中黑色虚箭头处残留了更多多次波且白色箭头处造成了更多一次波信号的泄漏，图23d、e中多次波压制和一次波的保护效果更好.以上对比证明在迁移学习下，本文方法能够获得良好的分离效果，略优于Radon法，且具有很好的抗噪稳定性.

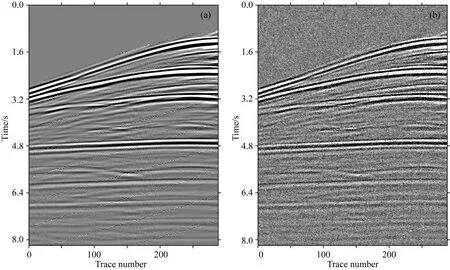
图21 未参与训练的全波场数据(a) 添加随机噪声前； (b) 添加随机噪声后.Fig.21 Full wavefield data not involved in training(a) Before adding random noise; (b) After adding random noise.

图22 分离得到的一次波结果(a) Radon法压制原始全波场中多次波； (b) 本文方法压制原始全波场中多次波； (c) 本文方法压制加噪后全波场中多次波.Fig.22 Primaries after separation(a) Radon method to suppress multiples in the original full wavefield; (b) The proposed method to suppress multiples in the original full wavefield; (c) The proposed method to suppress multiples in the full wavefield after adding noise.

图23 多次波压制前后的叠加剖面(a) 原始全波场叠加剖面； (b) 加噪后全波场叠加剖面； (c) Radon法压制原始全波场数据中多次波得到的叠加剖面； (d) 本文方法压制原始全波场数据中多次波得到的叠加剖面； (e) 本文方法压制加噪后全波场数据中多次波得到的叠加剖面.Fig.23 Stacked profiles before and after multiple suppression(a) Stacked profile of the original full wavefield； (b) Stacked profile of the full wavefield after adding noise； (c) Stacked profile obtained by suppressing multiples with the Radon method in the original full wavefield； (d) Stacked profile obtained by suppressing multiples with the proposed method in the original full wavefield； (e) Stacked profile obtained by suppressing multiples with the proposed method in the full wavefield after adding noise.

3 讨论

工业界中常用的多次波压制方法计算开销都较大，如SRME法和EPSI法等，尤其在处理三维地震数据时往往占用大量的计算资源.本文方法处理地震数据时，准备训练集和训练神经网络参数用时较大，但是迁移学习能够缩短训练过程计算时间，且一旦模型参数训练完成，深度神经网络可以实时处理地震数据，避免了常规方法下的大规模计算.

在本文提供的算例中，制作训练集时需要使用少量的不含多次波的共炮点道集数据作为标签数据.现阶段当各工区的标签数据不足时，我们需要借助Radon法、SRME法和EPSI法等方法得到标签数据，并使用迁移学习法将一个工区训练得到的深度神经网络参数用于另外一个工区地震数据的多次波压制中.随着标签数据的不断积累，我们可以使用不同工区的地震数据同时训练深度神经网络，进一步提升深度神经网络的泛化能力.

4 结论

本文使用深度神经网络来识别和重构一次波数据，并压制多次波数据.设计的神经网络结构类似于U-net网络，包括卷积编码部分和卷积解码部分.考虑到实际地震数据包含大量随机噪声，为了提升深度神经网络的抗噪能力和泛化能力，增加训练集数据量从而降低过拟合风险，本文通过旋转并在输入数据中加入不同强度的随机噪声得到増广训练数据集对，从而使用数据増广方法来训练深度神经网络.在神经网络测试阶段，使用训练好的神经网络参数，卷积编码部分能够提取地震数据中的一次波特征，卷积解码部分能够使用编码部分提取的特征来重构消除了多次波和随机噪声的地震数据.迁移学习能够让一个工区训练得到的神经网络参数用于另外一个工区的多次波压制中，取得了逼近甚至略好于传统方法的分离效果，提高了深度神经网络的泛化能力.在多次波的压制过程中，深度神经网络的训练占用了主要的计算开销，使用训练好的神经网络可以做到快速甚至实时地重构一次波.本文通过两个简单模型、Sigsbee2B模型三套模拟数据的实例和一套崎岖海底地震物理模型模拟数据的应用实例证明了本文提出的基于数据增广训练的深度神经网络方法在一次波重构和多次波压制中的有效性和抗噪稳定性.