致密油藏直井多层缝网压裂产量递减分析
代 立,尹洪军,袁鸿飞,孟凡嵩
(东北石油大学石油工程学院/提高油气采收率教育部重点实验室, 黑龙江大庆163318)
致密油藏储层渗透率低,渗流阻力大,常规开采无自然工业产量,需要对储层进行改造,增加产量[1]。缝网压裂是有效的开发手段之一,可以在地下形成裂缝网络[2-3],减小流体渗流阻力,改善储层渗透率,从而有效提高油井产量[4-5]。蒋廷学等[6]分别建立了有限导流和无限导流垂直裂缝井产能公式,并与实际产能进行对比,证明了方法的准确性。赵海洋等[7]建立了近井双重介质、远井均质的复合模型,对产量曲线进行了划分和分析。严谨等[8]在对产量的分析中考虑了远井段裂缝部分闭合,优化了裂缝的解释。刘雄等[9]考虑了压力敏感和启动压力梯度,应用解析法求解了致密油藏体积压裂直井模型,对产能进行了评估。R.A.Arche[10]建立了不考虑层间窜流的多层渗流模型,给出了不同层压力的统一公式。M.E.Osman[11]建立了均质无限大多层压裂井模型。尹洪军等[12]建立了单层体积压裂水平井渗流数学模型,将Blasingame 典型曲线划分为5个流动阶段。Blasingame 产量递减分析方法在油田已经得到了广泛应用[13-14]。已有模型主要研究了单层地层情况,对于直井多层压裂的研究较少,为此作者建立了直井多层缝网压裂渗流数学模型,可以更好地描述缝网压裂在储层中形成的裂缝网络,各层采用5 区模型[15-16],分析直井多层缝网压裂Blasingame 产量递减曲线,并对实例井进行解释应用。
1 物理模型
假设油藏呈n层特性,各层储层物性不相同,储层分层压裂,各储层裂缝为两翼对称缝,w为裂缝宽度,xif为第i层裂缝半长;各层划分为 5 个区域,F 为水力裂缝区,1 为改造区,2、3、4 为未改造区。各层改造区储层为双重介质,未改造区储层为基质,各层之间不发生窜流。直径多层缝网压裂物理模型如图1 所示。

图1 直井多层缝网压裂物理模型Fig.1 Schematic diagram of physical model of multilayer fracture network fracturing in vertical well
2 数学模型建立与求解
无因次变量定义如下。

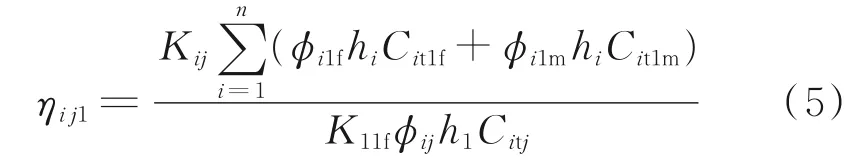
其中,j=1、2、3、4。
第i层人工裂缝无因次导压系数定义:
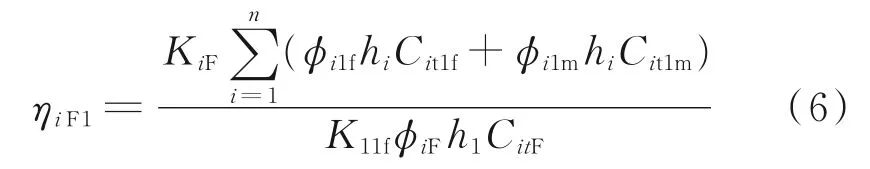
式中,h为储层厚度,m;K1m为改造区基质渗透率,m2;K1f为改造区微裂缝渗透率,m2;q为产量,m3/s;B为流体体积系数;μ为流体黏度,Pa·s;t为时间,s;φ为孔隙度;Ct为综合压缩系数,1/Pa;ω为储能比;x1为改造区半宽,m;wi为i层的人工裂缝宽度,m;λ为窜流系数;η为导压系数,m2·Pa/(Pa·s);Ctij为i层j区的综合压缩系数,1/Pa。其中,下标i表示层序号;j表示分区序号;D 表示无因次;F、1f、1m、2、3、4分别表示水力裂缝、改造区微裂缝系统、改造区基质系统、2 区、3 区、4 区。
根据假设条件建立各区数学模型,人工裂缝区数学模型为:


式中,s为拉氏算子;F为裂缝导流能力;e、d、a、τ、ζ、b、r、β、γ、d分别为计算过程中的中间变量。
3 产量递减分析
3.1 Blasingame 产量递减典型曲线

根据Blasingame 曲线定义绘制Blasingame 曲线,如图2 所示。

图2 Blasingame 产量递减典型曲线Fig.2 Blasingame production decline type curves
将典型Blasingame 曲线划分成7 个流动阶段:Ⅰ和Ⅱ为早期阶段,第Ⅰ阶段为双线性流,产量曲线与产量积分曲线重合,是斜率为-1/4 的直线;第Ⅱ阶段为改造区线性流,产量曲线斜率为-1/2;第Ⅲ阶段为窜流阶段,产量积分导数曲线出现一个“凹子”,基质向改造区微裂缝渗流;第Ⅳ阶段为改造区拟稳定流,产量、产量积分和产量积分导数曲线斜率皆为-1;第Ⅴ阶段为改造区与未改造区双线性流,产量曲线斜率为-1/4;第Ⅵ阶段为未改造区线性流,产量呈斜率为-1/2 的直线;第Ⅶ阶段为边界反映阶段,产量积分与产量积分导数曲线重合,产量曲线斜率为-1。
3.2 产量递减曲线敏感性分析
在裂缝总长度为400 m 的情况下,Blasingame产量曲线受不同裂缝半长组合的影响,结果如图3所示。由图3 可见,裂缝半长主要影响改造区线性流阶段及以后的流动,各层裂缝半长差异大,短裂缝储层渗流率先到达未改造区,未改造区渗流阻力大,产量递减快,曲线靠下。

图3 裂缝半长分析Fig.3 Fracture half-length analysis
图4 为裂缝导流能力分析。由图4 可知,不同裂缝导流能力组合主要影响早期阶段中的改造区线性流。当第一层裂缝导流能力一定时,第二层裂缝导流能力越大,产量曲线越靠上,产量递减越慢,裂缝导流能力越大,人工裂缝中流体流动越容易。
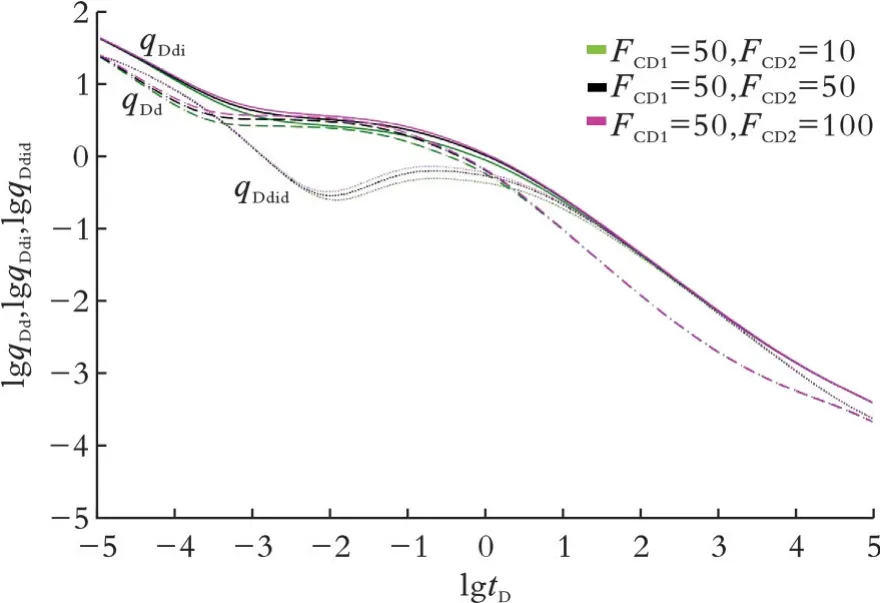
图4 裂缝导流能力分析Fig.4 Fracture conductivity analysis
图5 为改造区渗透率比值分析。由图5 可知,改造区渗透率比值(K1f/K2f)主要影响早期阶段和改造区拟稳定流,固定第二层的储层渗透率,渗透率比值越大,第一层改造区物性越好,改造区流体流动越容易,产量递减越慢。

图5 改造区渗透率比值分析Fig.5 Permeability ratio of SRV area analysis
图6 为不同储层改造体积组合对产量递减曲线的影响。由图6 可知,储层改造体积主要影响窜流阶段和改造区拟稳定流阶段。在总改造体积不变的情况下,当两储层的改造体积相等时,曲线最靠上,产量递减最慢;两储层的改造体积差异越大,曲线越靠下,产量递减越快。由于改造体积小的储层率先到达改造区拟稳定流,流体渗流变困难,产量递减变快。

图6 储层改造体积分析Fig.6 Stimulate reservoir volume analysis
4 实例分析
A 井为某油田一口直井,A 井的完钻深度为2 030 m,射孔井段1 975.6~1 891.0 m,射开有效厚度6.3 m,采用缝网压裂工艺对储层进行改造,压裂施工3 段4 条裂缝,压裂液总量2 690.1 m3,各储层基本参数见表1,生产动态曲线如图7 所示。

表1 基本参数Table 1 Basic parameters
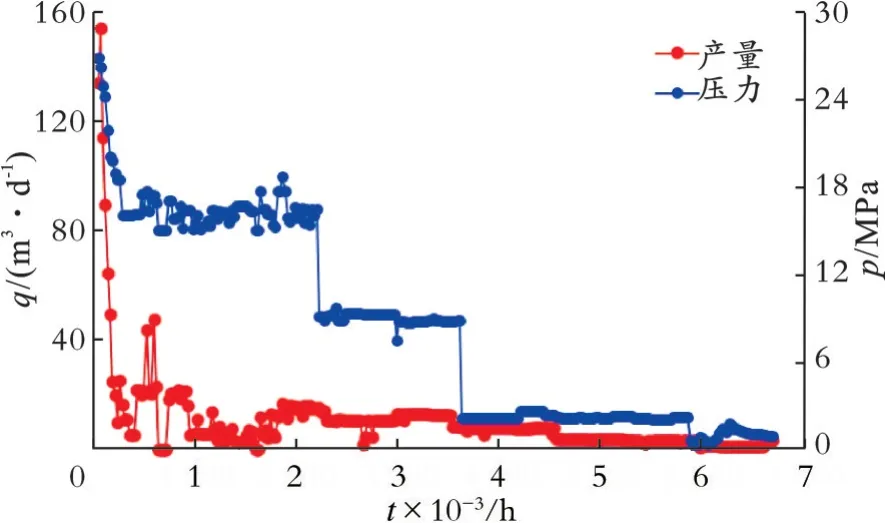
图7 A 井生产动态曲线Fig.7 Production transient curve of well A
根据所建立的多层缝网压裂直井产量递减模型,结合实测生产数据,利用曲线拟合方法对实例井资料进行解释,得到该井的储层和裂缝参数,Blasingame 拟合曲线如图8 所示,产量史拟合曲线如图9 所示,渗透率及导流能力见表2。
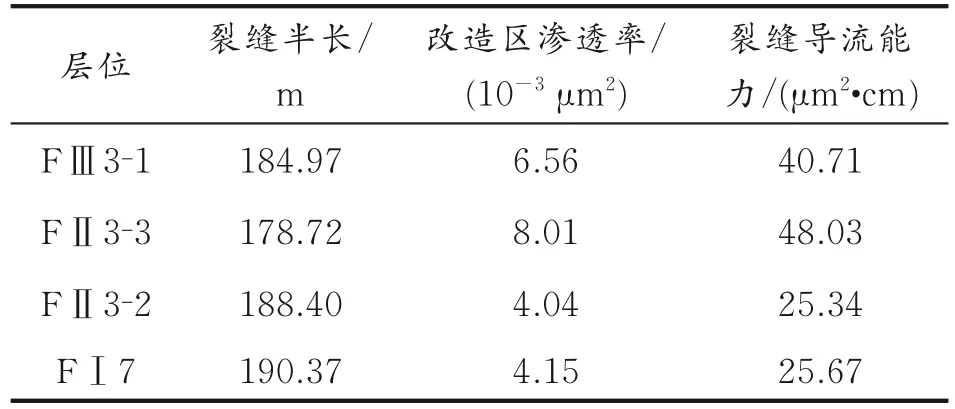
表2 渗透率及导流能力Table 2 Permeability and conductivity

图8 Blasingame 拟合曲线Fig.8 Blasingame matching curve

图9 产量史拟合曲线Fig.9 Production history matching curve
5 结 论
(1)基于渗流理论建立并求解了直井多层缝网压裂渗流数学模型,绘制了直井多层缝网压裂Blasingame 产量递减典型曲线,分析曲线特征分为7 个阶段。
(2)进行敏感性分析发现,在总裂缝半长一定时,各层裂缝差异大,短裂缝储层渗流率先到达未改造区,渗流阻力变大,产量递减变快;储层总改造体积一定时,各层改造体积差异大,Blasingame 曲线靠下;在第二层储层改造区渗透率一定时,改造区渗透率比值(K1f/K2f)越大,产量递减越慢。
(3)利用所建立的多层缝网压裂直井模型,对实测生产资料进行解释,获得了各层裂缝长度、改造区渗透率等参数,说明该模型对多层缝网压裂的直井产量分析有指导意义。

