季节性寒区高地下水位渠道衬砌形式试验研究

方建银，潘 优，党发宁，吴文平，高 俊

(西安理工大学 土木建筑工程学院，陕西 西安 710048)

我国西北的季节性寒区，灌区主要分布在河流的两岸，灌区灌渠衬砌主要采用全断面混凝土衬砌形式，在很大程度上提高了渠道输水效率[1-3]。然而，在地下水位较高的地方，传统的全断面衬砌形式阻断了地下水向渠内渗流的通道，致使地下水位不能快速地降低，在冬季非灌溉期，地下水冻结，造成渠道混凝土衬砌发生冻胀破坏事故频繁[4-6]。为了解决这一问题，格宾石笼的透水衬砌结构(透固体衬砌)孕育而生，该结构能够保证在非灌溉期地下水快速地渗入渠道内部，从而达到降低地下水的目的，保证了渠道衬砌结构的安全稳定，延长渠道的使用寿命[7-8]。然而，该种衬砌形式在灌溉期却会导致水资源大量渗漏浪费，渠道输水效率大大降低。因此，如何设计渠道衬砌形式保证渠道既不受冬季冻胀破坏又能够满足节水效益成为当前研究的重点[9-12]。

当前对渠道衬砌形式及渗漏特性的研究方法主要有理论分析法、数值计算法和模型实验法。经验公式法众多，但各结果差异较大，且不能对非稳定渗流进行计算[13-15]。解析法参数选取和计算过程复杂且只适用于特定的条件，一般在研究中不常用。目前渠道渗漏特性研究中的主流方法是将试验研究与数值模拟结合[16-19]。渠道渗流研究多集中于全衬砌或不衬砌渠道[20-22]，对于寒区透固体衬砌渠道渗流情况研究较少，主要集中于透固体布置位置[23]。

为此，本文设计了渠道渗漏模型试验箱，对渠水位、地下水位以及透固体衬砌宽度三种因素作用下的渠道渗流量进行了室内模型试验，并基于GeoStudio软件中的SEEP/W模块，进行了相应的数值模拟研究，将模型试验结构与数值模拟试验结果进行了对比分析，研究了各种工况下渠道输水的渗流规律，分析了透固体宽度对渗漏量的影响，为季节性寒区高地下水位渠道衬砌形式的选择提供了依据。

1 渠道渗流模型试验设计

1.1 试验系统

试验原型为宁夏引黄灌区骨干渠道混凝土板+渠底中部透固体衬砌段，透固体宽度为0.5 m、1 m、2 m不等。渠宽20 m，渠深3.5 m，设计水位2 m，衬砌边坡1∶1.75，长度方向取10 m。模拟渠道渗流试验在渗流模型试验箱内进行，模型箱示意图见图1。

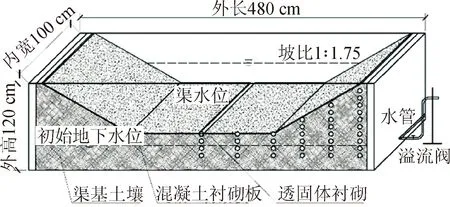
图1 模型试验箱整体示意图Fig.1 Overall schematic diagram of the model test box

模型箱长度方向为渠道横截面，渠道轴线沿着模型箱宽度方向。箱体采用有机玻璃制造，侧向加钢肋梁以提高其抗弯曲刚度。在槽身两侧和槽底装测压管，测量渗流场各点的水位高程。加装一个溢流阀控制地下水位初始高程，同时用于测量渠底渗流量。

试验用土取自宁夏引黄灌区附近，压实制作渠基土，利用双环法分别对原型渠基土和模型地基土壤进行了土性参数试验。测量得原型土壤质地为粉细砂土，孔隙比0.7，渗透系数为2.49×10-5m3/s；模型土壤质地为砂土，孔隙比0.52，渗透系数为1.96×10-5m3/s。模型渠基土制作过程中因压密与震实作用，使得土体较为致密。颗分试验所测土壤颗粒级配良好，与现场控制条件较为一致，渗透试验结果可靠。制作完成的试验箱见图2和图3。

图2 室内模型试验箱Fig.2 Indoor model test chamber

图3 调节地下水位的装置Fig.3 Device for adjusting groundwater level

本次试验采用稳定渗流法进行测试，试验条件设定的优先次序为：衬砌工况-地下水位-渠道水位。首先进行模型渠道衬砌，利用模型模拟透固体衬砌时，在渠道模型表面预设一定的宽度不做衬砌处理，其余表面浇筑混凝土作为防渗结构，混凝土防渗体制作按渗流量等效原则通过厚度控制。然后向渠內缓慢注水，待模型土壤饱和后，调整溢水设备，通过观测测压管水头使地下水位达到设定工况。最后连接自来水管将水缓慢注入模型灌渠至设定渠水位，渗流过程中及时向渠道补水以保持渠道水位的设定高度。渗流一段时间后，用容器开始测量溢流阀处的渗水量。每隔10分钟测量一次容器中的水量，直至渗流稳定。连续3次测量值之间差值不超过2%时停止测量，并以最后三次数值的平均值作为所测工况条件下的渗流量。重复上述步骤进行下一工况测量。

1.2 试验原理

模型试验箱设计遵从几何相似、运动相似和动力相似，并保证透水边界和隔水边界条件与原型一致，即模型上表面为透水边界，下部为隔水边界，两侧及渠内为定水头边界。

1)几何相似

模型中的渗流区与原型渗流区在长、宽、高等线性尺寸方面，遵守一定的比例，用aL表示线性比例，则有：

(1)

(2)

式中：L和b分别为渠道的长度和宽度，m；h为渠内水头高度，m；A为渠道投影面积，m2；下角标H表示原型数值；下角标m表示模型的相应值。

2)运动相似

模型和原型中渗流质点的速度成固定比例，用av表示速度比例，则有：

(3)

式中：v为质点流速，m/s；n为渠底土壤孔隙度；t为渗流质点流过相应线段所需的时间，s；av为速度比例；an为孔隙度比例；at为时间比例；其他符号意义同前。

3)动力相似

因多数天然渗流都是层流，其惯性力可以忽略不计，所以模型渗流要保持层流状态。原型渗流和模型渗流都可用Darcy定律表示为：

(4)

(5)

取二者比值，结合式(1)，并将av用式(2)代替得：

(6)

式中：K为渗透系数，m3/s；aK为渗透系数比例(aK=kH/km)；其他符号意义同前。

由以上各式可知，只要根据勘探资料查明了天然渗流区的长度、宽度和边界水头，试验测定土壤各项渗透指标，结合试验设备条件选好适当的线性比例aL，按式(1)就能求出模型的相应尺寸Lm，bm和hm；以现有的土壤制成模型，然后根据该土壤的渗透系数和孔隙度求出aK和an。

本次试验采用稳定渗流方法测试。如果研究的是非稳定运动，还得知道试验进行的时间。这时，在确定aL，aK，an的条件下，时间比例就不是任意的，而应按式(3)求出at，再根据天然渗流的实际过程计算tH和tm。

4)模型原型流量转换

观测的模型流量，可按下述方法转换为原型渗流的流量。按Darcy定律：

(7)

(8)

取二式比值，按相似比例，可得渗流量换算式：

(9)

式中：Q为渗流量，m3/s；其他符号意义同前。

需要指出的是，当模型比尺为aL∶1时，利用式(9)计算得到的是长度为aL的渠道区间的渗流量。

定义渠道衬砌节水系数ε，该参数等于渠道某种衬砌方法节约的水量与未衬砌时渗漏水量之比：

(10)

式中：Q渗为渠道未衬砌时的渗流量，m3/s；Q衬为采取衬砌措施后的渗漏量，m3/s。

1.3 试验设计

本次试验取aL=10，即模型比尺为10∶1，aK=KH/Km=2.49×10-5/1.96×10-5=1.27，模拟砂土地基上底宽20 m的衬砌渠道渗流情况。

试验模拟的水位条件为将原型各水位按模型比尺缩小设计。规定地下水位和渠底齐平时为0 m，渠底以上为正，渠底以下为负。试验时，渠水位取设计水位、70%设计水位和50%设计水位；地下水位取-2.5 m、-1.5 m、-0.5 m、0、1/3设计水位、2/3设计水位；渠底中部透固体宽度为0.05 m、0.2 m、1 m、2 m和5 m。针对具体因素的试验工况设定为如下。

1)渠水位

原型渠底透固体衬砌宽度为2 m，地下水位为-1.5 m，渠水位分别为1 m、1.4 m和2 m；对应模型渠底中部透固体衬砌宽度为20 cm，地下水位-15.0 cm，渠水位分别为10.0 cm、14.0 cm和20.0 cm。

2)地下水位

原型渠底透固体衬砌宽度为2 m，渠水位2 m，地下水位分别为-0.5 m、0 m、0.67 m和1.33 m；对应模型渠底透固体宽度20 cm，渠水位20 cm，地下水位分别为-5 cm、0 cm、6.7 cm和13.3 cm。

3)透固体宽度

原型渠水位取2 m、地下水位-2.5 m，渠道衬砌形式为不衬砌和透固体衬砌，透固体宽度分别为0.05 m、0.2 m、1 m、2 m和5 m；对应模型渠水位20 cm、地下水位-25 cm，透固体宽度为0.5 cm、2 cm、10 cm、20 cm和50 cm。

1.4 试验结果分析

1)渠水位对透固体衬砌渠道渗流影响

试验测得渠水位10.0 cm、14.0 cm和20.0 cm时模型渗流量分别为9.07 mL/s、10.45 mL/s、13.47 mL/s。

以地下水位-15 cm，渠水位10 cm，渠道中部开缝20 cm时测得的模型渗流量Qm=9.07 mL/s为例，根据式(9)，将其换算为地下水位-1.5 m，渠水位1 m，渠道中部开缝2 m时单位长度渠道原型渗流量。

具体计算过程：QH=1.27×102×9.07/10=115 mL/s=1.15×10-4m3/s，单位水头渗流量=1.15×10-4/2.5=1.96×10-5m3/(s·m)。同理,可求得渠水位1.4 m和2 m工况下的渗流量为4.59×10-5m3/(s·m)和4.89×10-5m3/(s·m)。

可得渗流量随渠水位的变化关系，见图4。

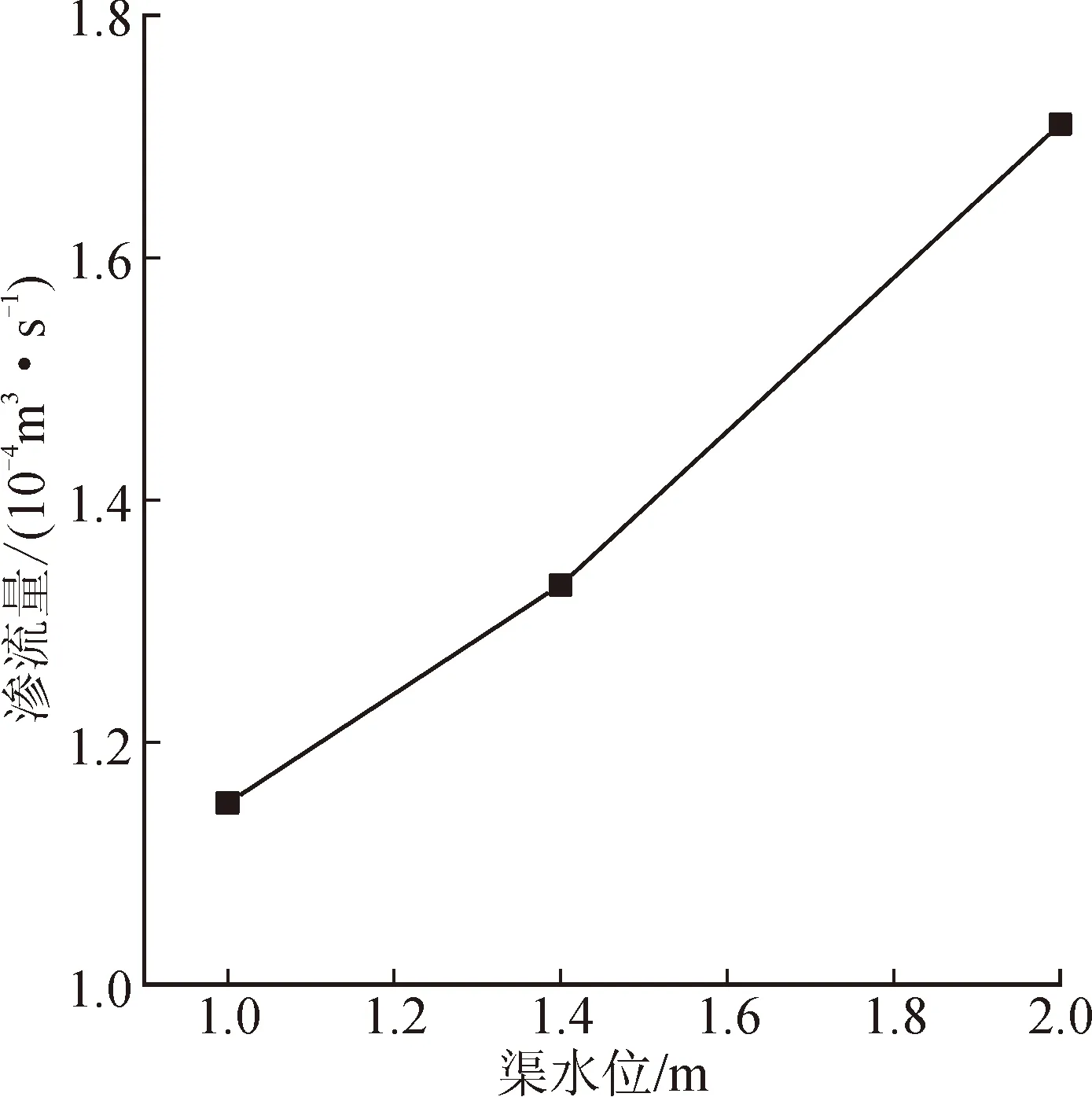
图4 渠水位对透固体衬砌渠道渗漏影响Fig.4 Influence of canal water level on the seepage of canal with permeable structure

由图4可以看出，在地下水位不变时，透固体衬砌渠道渗流量随渠水位的升高近似呈线性增大关系，渠水位越高，渗流量越大。当渠水位升高时，渠道内外水头差逐渐增大，渗流量因此增大。当渠水位为1 m时，渗流量1.15×10-4m3/s，渠水位逐步增加至2 m，渗流量增长0.49倍。不同水位差条件下的单位水头渗流量基本相等。

2)地下水位对透固体衬砌渠道渗漏影响

试验测定渗流量见表1，渗流量随地下水位的变化关系图见图5。由图5可以看出，在渠水位不变的条件下，透固体衬砌渠道渗流量随地下水的升高近似呈线性减小关系，地下水位越高，渗流量越小。地下水位逐渐抬高，渠道内外水头差减小，渠道渗流量逐渐减小。当地下水位为-1.5 m时，渗流量1.71×10-4m3/s，地下水位依次增加至1.33 m，渗流量减少0.73倍。不同水位差条件下的单位水头渗流量基本相等。

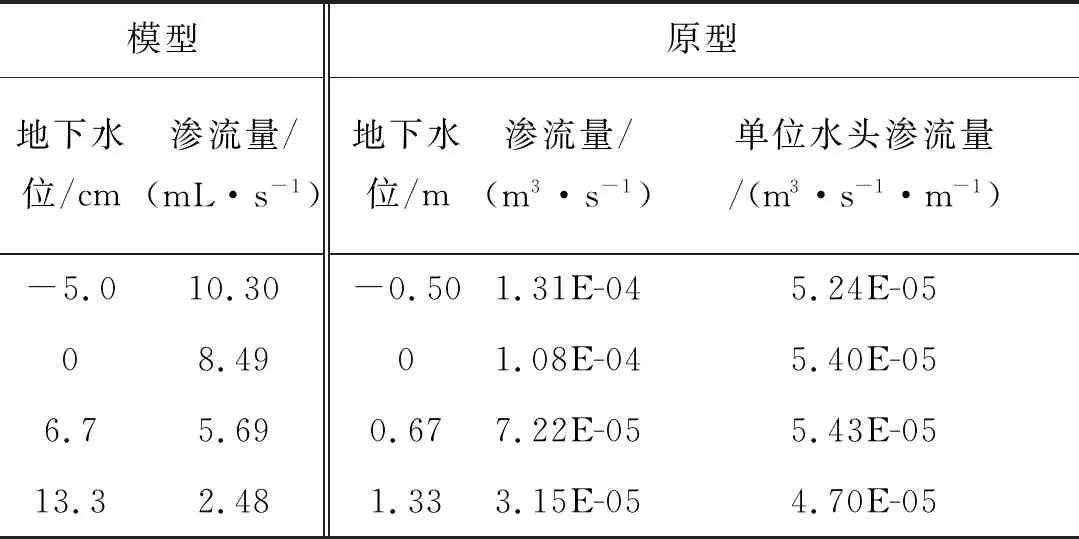
表1 不同地下水位时渠道渗流量试验结果Tab.1 Canal seepage test results at different groundwater levels

3)透固体衬砌宽度对渠道渗漏影响

试验测定透固体宽度与渗流量关系见表2。

表2 不同透固体宽度时渠道渗流量试验结果Tab.2 Canal seepage test results with different solid widths

单位水头渗流量随透固体宽度的变化关系见图6。由图6可以看出，透固体宽度对渠道渗流量有影响，透固体宽度越大渠道渗流量也越大，渗流量与透固体宽度不成线性关系。透固体衬砌宽度为0.05 m时，渠道渗流量1.94×10-4m3/s，宽度增加到100倍为5 m时，渗流量只增加了21%，在数量级上没有变化。图6显示，透固体衬砌存在临界宽度，当透固体宽度小于临界宽度时，渗流量变化率较大；当透固体宽度大于临界宽度时，渗流量对缝宽不是很敏感，随缝宽变化趋势不明显。

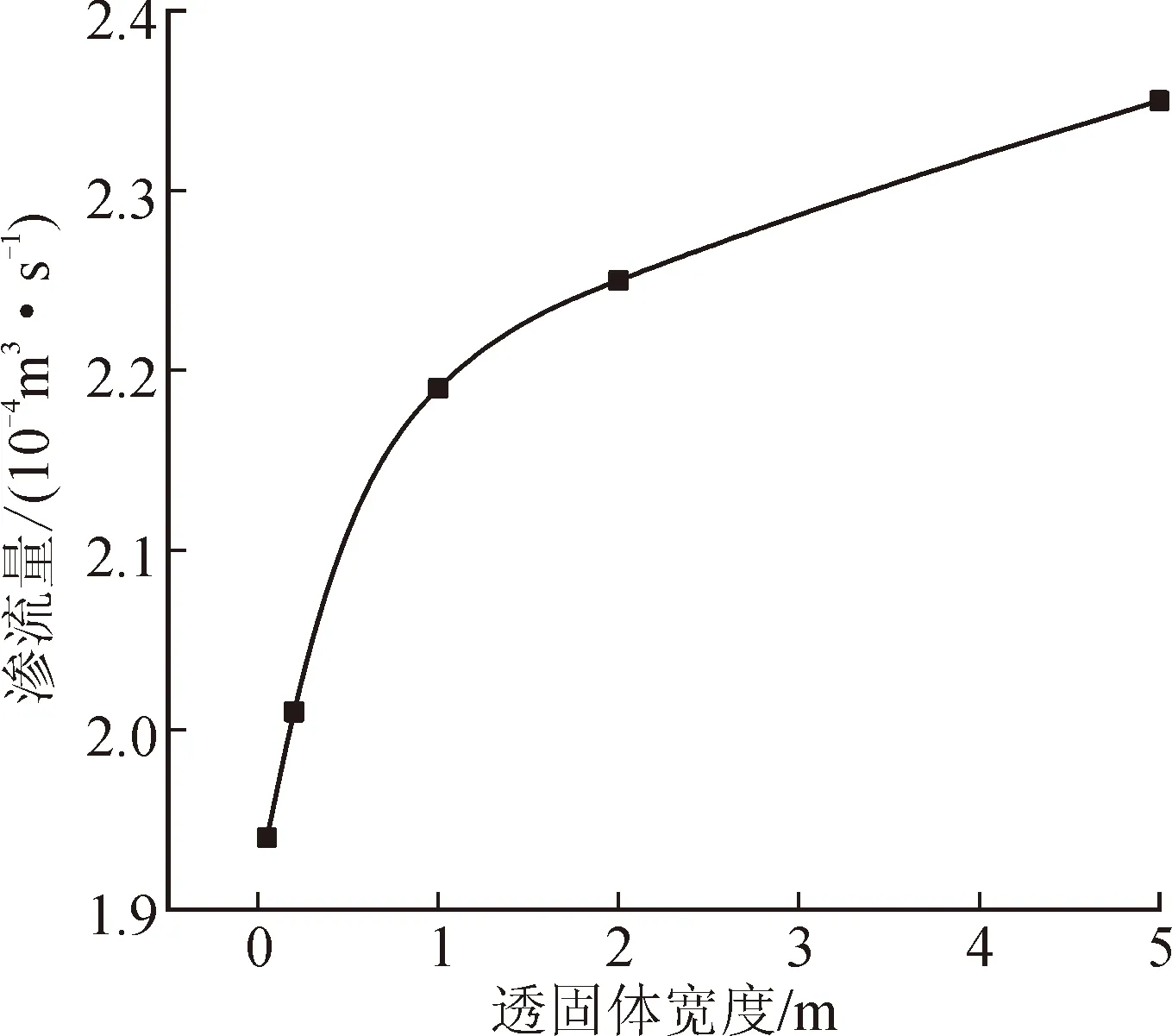
图6 透固体宽度对渠道渗漏影响Fig.6 Influence of the width of the permeable structure on channel leakage

计算得透固体宽度为1 m时衬砌节水系数0.22，节水效果较好。透固体宽度为0.05 m时节水系数最大，为0.31，宽度5 m时节水系数最小为0.16。

2 数值试验

2.1 数值模型

为了与室内模型试验结果进行对比分析，本节利用GeoStudio软件中的SEEP/W模块进行渠道渗漏的有限元数值试验研究。

模型取渠道原型尺寸，渠底宽度为20 m，深度为3.5 m，坡比取1∶1.75。渠坡顶部向两侧左右岸各延伸500 m，渠底以下设置100 m地基厚度。对渠道衬砌部分进行网格加密，指定相应水头及边界条件。

渠道局部模型及有限元网格划分见图7，图8为渠道开缝衬砌示意图，将模型两岸及地下延伸缩短之后的模型边界示意图见图9。

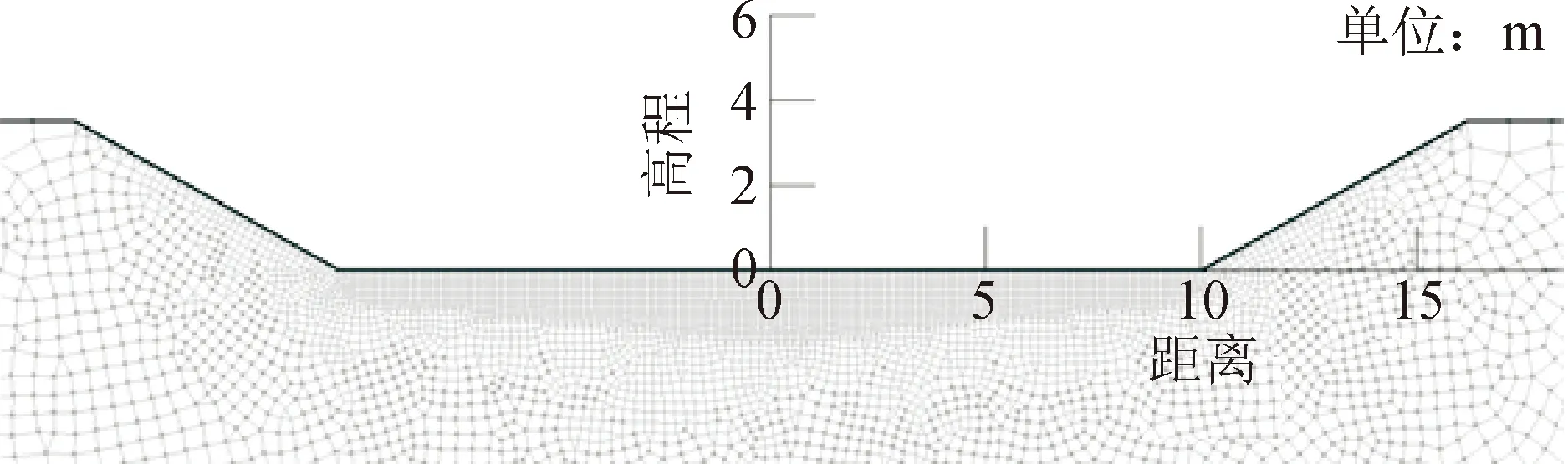
图7 渠道局部模型及网格划分图Fig.7 Partial channel model and grid division diagram

图8 渠道衬砌工况局部图Fig.8 Partial view of channel lining working condition

图9 渠道模型边界示意图Fig.9 Schematic diagram of the channel model boundary

模型上表面带点的线表示渠内水位，为定水头边界。两侧带点的线表示地下水位，为定水头边界。上表面带三角的线表示潜在渗流面，为透水边界。模型底部为不透水边界。

依据1.3节试验设计工况，为模型进行模拟参数设定，其中渠水位和地下水位影响因素模拟采用和室内试验相同工况条件。室内试验得知透固体存在临界宽度，本节对透固体宽度缩小间隔进行渗流模拟，并对砂壤土和砾石土渠基条件下的透固体临界宽度进行研究，具体参数设定为土壤质地：砂壤土、砂土、砾石土；透固体宽度：0.01 m、0.05 m、0.1 m、0.2 m、0.4 m、0.8 m、1 m、2 m、5 m；渠水位2 m；地下水位-2.5 m。

计算模型各材料的渗透系数按表3选取。

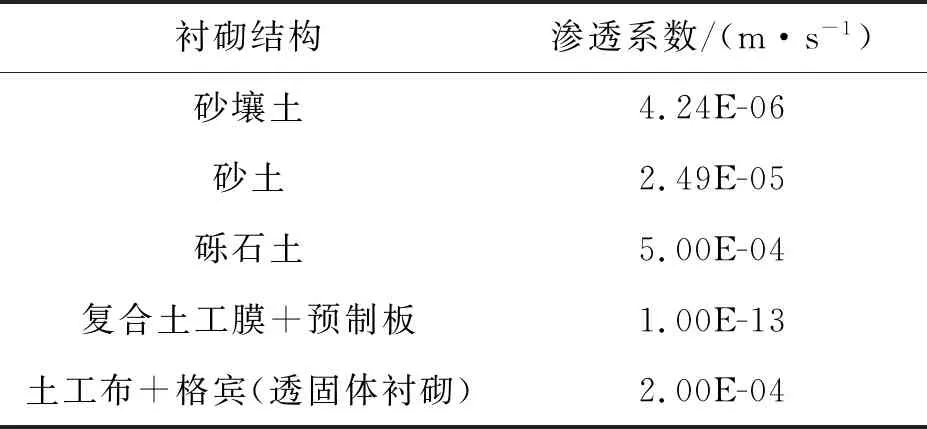
表3 渗透系数选取表Tab.3 Selection table of permeability coefficient

2.2 试验结果对比分析

分别模拟了与前述室内试验相同工况的渠道渗漏情况，给出部分渗流量结果局部云图见图10。

图10 渗流量计算结果局部云图Fig.10 Partial cloud diagram of leakage calculation results

1)水位对透固体衬砌渠道渗流影响

绘制渠水位、地下水位与渠道渗漏关系，见图11。

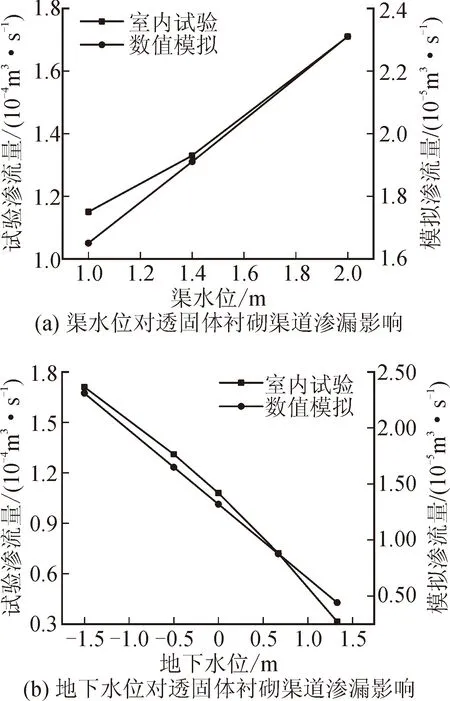
图11 水位与渠道渗漏关系Fig.11 Relationship between water level and channel leakage

将数值模拟结果与室内试验结果进行对比可知，数值计算与模型试验所得结果规律一致，均表明渠水位、地下水位对渠道渗流量有影响。渠水位越高，渠道渗流量越大且近似为线性增大关系。渠道渗流量随地下水位升高呈线性降低趋势。

2)透固体衬砌宽度对渠道渗漏影响

根据模拟结果绘制出三种渠基土壤质地下渗流量随透固体宽度的变化图，见图12。

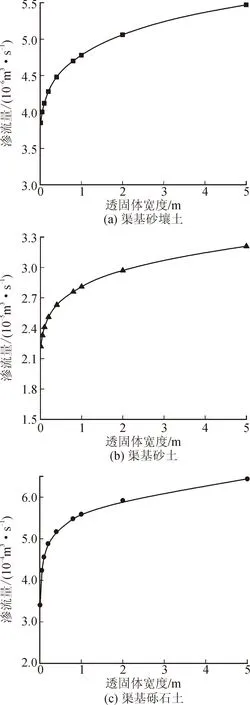
图12 透固体宽度与渠道渗漏关系Fig.12 Relationship between the width of permeable solids and channel leakage

由图12可以看出，渠基土性不同时，透固体衬砌宽度对渠道渗流量均有影响，透固体宽度越大渗流量越大，但二者不成线性比例。无论渠基土壤为哪种质地，临界宽度均为0.4 m。透固体宽度小于0.4 m时，渗流量变化明显，透固体宽度大于0.4 m后，渗流量随缝宽变化不是很明显。

3 结 论

1)本文设计了一种渗漏试验室内模型，该模型试验箱可模拟季节性寒区灌渠不同渠基土壤、不同渠水位、不同地下水位以及不同衬砌形式的渠水渗漏情况，可以为评估节水改造工程的节水效果、为灌渠防渗衬砌方案和灌渠水利用系数等研究提供技术支持。

2)渗流量受渠水位与地下水位差的影响较大，水头差越大，渗流量越大。渗流量随透固体宽度增大而增大，透固体存在临界宽度(约为0.4 m)，小于临界宽度时，渗流量变化显著，大于临界宽度时，渗流量变化不是很敏感，可以据此确定渠道衬砌的结构形式。

3)从灌溉节水考虑，建议采取较小的透固体衬砌宽度，其衬砌节水系数较高，从渠道防渗及保护衬砌结构角度考虑，以拐点0.4 m作为透固体宽度为宜。