基于改进随机森林算法的工业过程运行状态评价

常玉清 孙雪婷 钟林生 王福利,2 刘英娇

1.东北大学信息科学与工程学院 沈阳 110819 2.流程工业综合自动化国家重点实验室(东北大学)沈阳 110819

工艺操作的安全性和优化性是工业界近几十年来备受学术界和工业界关注的两个关键问题[1].然而,由于扰动、噪声等不确定因素的存在,安全性和最优性都可能发生恶化,这会导致运行性能的下降.因此,及时、准确地掌握过程运行状态,对于提高企业经济效益、生产效益和产品质量都有重要意义.而传统的过程检测仅仅是监测生产过程是否正常,对于异常的生产过程剖析原因通过调整使生产继续正常运行.为了获得更高的经济效益,需要得到整个工艺过程的优劣状态,因此相关学者提出了运行状态评价的概念[2-3].运行状态评价是指在生产过程正常运行的前提下,对实际生产过程的运行优劣进行识别与判断,当运行状态处于“非优”时,通过及时调整操作,使运行状态达到“优”.因此,对运行状态评价的研究具有重要的理论意义和应用价值.

目前,针对运行状态评价学者们进行了一定的研究.案例推理[4]方法评价速度快,且推理评价过程包含了学习和归纳,有一定实际意义.粗糙集理论[5]能够有效地分析和处理不完备信息,并从中发现隐含的知识,揭示潜在规律.它的根本思想是在保持条件属性相对于决策属性不变的前提下,通过属性约简和值约简等过程,挖掘数据内涵的规则,在对定性和定量变量混合的数据处理上具有较好的效果.人工神经网络[6]学习能力强,能够表达非线性的映射关系,在非线性过程的运行状态评价中有应用.针对小样本情况,研究者提出灰色关联分析法[7].模糊评价[8]是最常用的评价方法之一,它既符合决策过程中信息的可用性和不确定性,又符合人的认知的模糊性.针对多模态过程运行状态评价,邹筱瑜等[9]提出了基于高斯混合模型的评价方法,确保特征提取的准确性,避免了模态划分问题.文献[10]提出了多种工业过程运行状态评价方法,但其是基于定量变量,对于定性变量的处理并未提及.

但在实际生产中,复杂工业过程运行环境差、检测技术不完善,导致过程定量信息与定性信息共存,限制了传统的运行状态评价方法的应用.其中,定量信息指用数值大小描述的变量信息,定性信息指通过语义定性描述的变量信息.本文通过对复杂工业过程进行深入研究,提出了基于随机森林的运行状态评价方法,随机森林的特点是能够同时处理定量信息和定性信息,且无需对数据进行复杂的预处理.

为了提升随机森林的性能,学者们提出了多方面的改进方案.文献[11]通过操作训练集和训练特征定义了一组新的随机森林分类器.Tuv 等[12]、Paul 等[13]提出通过特征选择来去除不重要特征、减小特征冗余以减小特征空间.文献[14]提出了随机森林中一种有效的聚合方法—交替决策森林,该方法将随机森林的训练归为全局损失最小化问题.在投票环节,提出一种加权投票方法为不同决策树赋予不同的投票权值[15].但是针对决策树之间的冗余问题,以上方法未有提及.为了解决该问题,本文提出一种基于改进的随机森林运行状态评价算法,采用互信息计算随机森林中不同决策树之间的相关性以及每棵决策树的评价精度,剔除相关性大且精度低的决策树.同时,为了解决投票权重问题,将评价精度转换成决策树的权重,增加精度高的决策树投票权重,降低精度低的决策树投票权重,进而提高随机森林的评价精度.

本文主要以湿法冶金的氰化浸出过程为研究对象,分别利用传统的随机森林算法和改进的随机森林算法建立运行状态评价模型,通过对评价结果的对比分析,验证了所提方法的正确性和有效性.

1 随机森林

1.1 随机森林定义及性质

随机森林(Random forests,RF)算法是Breiman 于2001年提出的一种分类和预测算法,其本质是将Bagging 算法和随机子空间算法结合起来[16-18].随机森林是一种以决策树为基分类器的集成学习模型[19].它是利用bootstrap 抽样方法生成多个训练集,针对每个训练集建立一个决策树模型,然后通过投票方式集成所有决策树的预测结果.RF 具有很高的预测准确率,对异常值和噪声具有很好的容忍度[20],且不容易出现过拟合,并且训练速度较快,目前已广泛应用于各种分类及预测问题.

定义1.随机森林是一组由多个决策树分类器组成的集成分类器,随机向量独立同分布.当输入待分类样本后,每个决策树分类器通过简单投票(即少数服从多数)得出分类结果.

1.2 随机森林的生成

2 基于改进随机森林的工业过程运行状态评价

工业过程运行状态评价是指在生产过程正常运行的前提下,通过一定的方法对实际生产过程的运行状态进行识别与判断,当运行状态处于“非优”时,及时调整生产操作,以使状态达到最佳.其实质是通过学习历史数据,对在线数据的运行状态进行分类评价.

在用传统随机森林算法进行运行状态评价时,由于其会生成相似度较高的决策树,造成模型冗余,同时在投票环节,所有决策树权重相同,忽略了不同决策树的性能差异.基于上述问题,本文提出了一种基于互信息的加权随机森林算法(Mutual information weighted random forest,MIWRF).利用互信息计算任意两棵决策树的相关性,对于相关性较大的决策树,只保留评价精度最高的决策树,从而形成新的随机森林,并将评价精度转化为投票权重,最终得到冗余更小,评价精度更高的随机森林模型.

2.1 改进的随机森林算法

在文献[21]中,Krogh 和Vedelsby 提出了一种误差-分歧分解规则,该规则表明个体学习器准确性越高,多样性越大,则集成效果越好.基于该结论,我们提出用互信息来度量个体学习器的多样性和准确度.

2.1.1 算法描述

在信息论中,互信息用来衡量两个变量之间的相互依赖关系[22],换而言之,它表示一个随机变量中包含另一个随机变量的信息量.对于两组给定随机变量X,Y,它们的互信息表示为

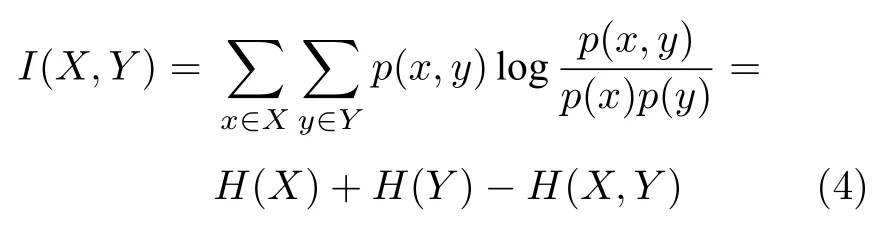
其中,p(x,y)为X,Y的联合概率分布,p(x),p(y)分别为X,Y的边缘概率分布,H(X)是X的信息熵,其计算式为

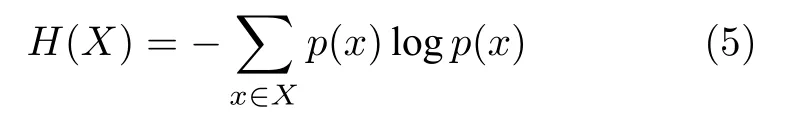
其中,p(xi)表示事件xi发生的概率;H(Y)是Y的信息熵,H(X,Y)是联合熵,其计算式为

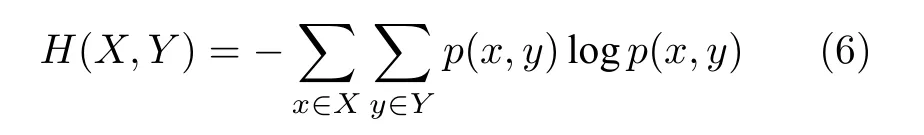
当变量X和Y完全独立时,互信息最小,结果为0,说明两个变量之间不包含重复信息.反之,互信息越大,两个变量的相互依赖性越大,即两个变量之间的重复信息越多.

对于随机森林中的决策树hi(i=1,2,···,K),I(hi,hk)(k /=i)表示决策树hi与hk的互信息.本文采用I(hi,hk)(k /=i)来计算决策树hi与hk之间的相关性,即重合度.其计算式为

其中,yi(i=1,2,···,K)为第i棵决策树的输出状态.I(hi,hk)的值越大,说明两棵决策树的相关性越大,所描述的信息的重合度越高.通过计算任意两棵决策树的互信息,将互信息值大于阈值ε的决策树合为一组.I(hi,y表示决策树hi与实际标签y的互信息,即决策树hi的输出评价结果与实际评价结果之间的相关性.其计算式为

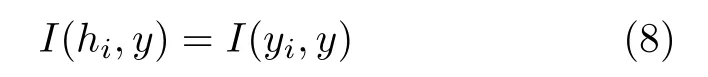
I(hi,y)的值越大,说明决策树hi的评价精度越高.最后将相关性较小、精度较高的决策树组成新的随机森林.

算法具体过程如下:

步骤1.获取训练集D={(x1,y1),(xxx2,y2),···,(xxxN,yN)},验证集T={(xxx1,y1),(xxx2,y2),···,(xxxL,yL)},xxxi(1×M)为评价属性,yi(1×1)为评价标签.

步骤2.通过Bootstrap 抽样从D中抽取n(n ≤N)个样本,重复K次,得到K个训练集.

步骤3.对于每一棵决策树的内部节点,从样本M个属性中随机抽取m个属性,选择m个属性中的最优分裂属性作为该节点的测试属性.

步骤4.生成K棵完全随机决策树,组成随机森林R={h1,h2,···,hK}.

步骤5.将验证集T输入R中得到评价结果.

步骤6.根据评价结果,依次计算每棵决策树与其余决策树的相关性.将所有I(hi,hk)(k /=i)大于阈值ε的决策树合为一个决策树组.若hi与其余所有决策树相关性均小于等于阈值ε,则该决策树单独作为一组.

步骤7.再将组外决策树按照顺序重复步骤6,直至全部决策树分组完成.

步骤8.根据精度I(hi,y)获取每组中精度最高的决策树.

步骤9.将所获取的决策树组成新的随机森林.

2.1.2 加权投票

对输入的样本数据进行评价时,传统的随机森林在投票时每棵决策树的投票权重相同,忽略了不同决策树的评价精度对最终结果产生的影响[23],降低了随机森林整体的评价精度.

为了增加评价精度高的决策树和降低评价精度不高的决策树对最终评价结果的影响,本文提出了加权投票方法,将评价精度转化为决策树的投票权值.在传统随机森林精简后,新随机森林中的决策树评价精度矩阵ACC为[15]

其中,accqp表示第p棵决策树对于第q种运行状态的评价精度,其中,p=1,2,···,P,q=1,2,···,Q,Q为评价结果的等级数目,P为改进后决策树数量.通过将验证集T代入新的随机森林,并计算每棵决策树对于每一类的输出结果的正确率获得.

根据评价精度矩阵,定义权重矩阵W为

其中,wqp表示第p棵树对于第q种运行状态的权重,其计算式为

基于互信息的加权随机森林算法(MIWRF)的具体流程如图1.

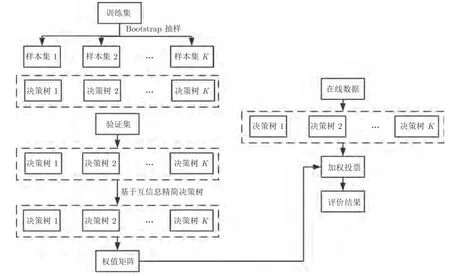
图1 基于互信息的加权随机森林算法Fig.1 Weighted random forest algorithm based on mutual information

2.2 运行状态评价模型的离线建模

由于随机森林能够同时处理定量和定性信息,同时无需对正常数据进行复杂的预处理.在获取离线建模数据后,生成包含K棵决策树的初始随机森林评价模型R.同时用验证集T精简初始模型.根据第2.1 节所提方法,计算任意两棵决策树的相关性I(hi,hk)(k /=i),将相关性大于阈值ε的决策树合为一个决策树组,再计算组内决策树的评价精度I(hi,y),留下组内精度最高的决策树,生成包含棵P决策树的新的随机森林评价模型R′.在投票环节,以评价精度为基础生成随机森林的权重矩阵W.

2.3 在线评价

3 金湿法冶金浸出过程的运行状态评价

3.1 湿法冶金浸出过程

湿法冶金指使用一定成分的无机水溶剂或有机溶剂与经选矿富集的精矿相接触[24],通过化学反应使矿石中的有用金属转入溶液中,再从溶液分离富集所含的金属离子,最后以单质或其化合物的形式提取的方法.本文以高铜线为研究对象,研究其氰化浸出过程.氰化浸出过程是湿法冶金中比较重要的一步,浸出的好坏对黄金的产量和综合经济效益的高低有直接影响,因此对浸出过程进行运行状态评价具有重要意义.

氰化浸出是指将氰化钠溶液与含有待提取金属的矿石进行化学反应,提取其中的有价金属或其化合物.浸出工序包含四个浸出槽,分别向第1、2 和4 浸出槽内加入氰化钠溶剂,并向每个浸出槽中通入空气以使氧气溶于矿浆中并搅拌矿浆,使金单质与氰化钠充分反应,最终以金氰离子形式存于液相中.理论上氰化浸出的化学方程式如式(14).为了防止氰化钠被水解产生剧毒气体HCN 或者被二氧化碳分解消耗,常用石灰乳作为保护碱.

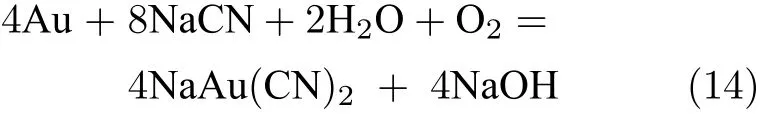
3.2 运行状态影响因素分析

在氰化浸出过程中,影响因素众多,对可能影响浸出结果的因素分析如下[25-28].

1)NaCN 添加量和浓度

氰化钠添加量和浓度会影响浸出过程的反应速率和浸出率的高低,氰化钠的添加量直接影响溶液中氰化钠的浓度.NaCN 浓度过低,金的溶解速率较低,会使得一定时间内的反应不充分;NaCN 浓度过高,会增加生产成本.在实际生产中,NaCN 浓度固定不变,因此不考虑 NaCN 浓度对浸出率影响;NaCN 添加量是可以在线获得的定量变量.

2)搅拌强度和氧浓度

湿法冶金的浸出过程主要通过通入空气对浸出槽内的液体进行搅拌,使其充分反应,提高反应速率,其在充入空气的同时也带入了反应所需的氧气.在这里,用空气流量大小来体现搅拌强度和氧浓度.空气流量是可以在线测量的定量变量.

3)初始金品位和矿浆浓度

初始金品位和矿浆浓度直接影响着整个浸出过程的运行状况及浸出率的高低.矿浆浓度直接决定其中的反应物的扩散速度,初始金品位影响着金的浸出量.在实际生产过程中,受生产条件的限制,这2 个变量无法在线获得,只能由专家给出定性估计.

3.3 运行状态评价仿真实验

综合第3.2 节影响因素分析,本文以氰化浸出过程的浸出效果作为评价指标,选取19 个与该指标密切相关的过程变量,列于表1 中.氰化浸出过程是一个定性信息与定量信息共存的过程,根据评价指标及该过程对运行状态评价的具体要求,将浸出过程的运行分为优、次优和非优三个等级.本节将所提方法应用于我们课题组开发的金湿法冶金半实物仿真平台中,此仿真平台模拟了所研究的金湿法冶金生产过程.经过长时间的实践、修正和完善,此平台可以较为准确地模拟该湿法冶金生产过程,为实际生产决策提供参考.从金湿法冶金仿真平台采集5 000 组训练数据,其中,4 000 组数据作为训练集用来建立传统随机森林模型,1 000 组数据作为验证集.实验选取参数决策树数量K=100 ,评价属性数量m=5 ,阈值ε=0.85 ,H=5 .

表1 浸出过程变量列表Table 1 Key variables affecting leaching efficiency

为了验证本文算法的有效性,从仿真平台采集850 组数据作为测试样本,设计了如表2 的实验,实验模拟了由于一次浸出浸出槽4 氰化钠添加量不足导致的运行状态评价等级从“优”逐渐转化为“次优”,再转化为“非优”.同时分别建立了传统随机森林算法在不同决策树数量下的评价模型,对比改进前后模型决策树的数量可知改进算法在提高精度的同时降低了模型的复杂度.

表2 浸出过程实验设计Table 2 Experiment of leaching process

3.4 实验结果分析

运行状态等级的概率计算结果如图2,最终评价结果如图3.由于实际采集的样本会存在一定程度的波动,因而图中的概率计算会出现一些波动尖点.从图2 的概率计算结果可以看出,在前160 个样本点,等级“优”的概率最大:从161 个样本点开始,等级“优”的概率逐渐减小,等级“次优”的概率逐渐增大.314～479 个样本点中,等级“次优”的概率最大:自480 个样本点起,等级“次优”的概率逐渐减小,等级“非优”的概率逐渐增大.从第637 个样本点起,等级“非优”的概率最大.根据运行状态等级在线评价策略,运行状态等级评价结果为:1～317 个样本点,运行状态等级评价结果为“优”等级:318～640 个样本点,为“次优”等级:641 个样本点起,为“非优”等级.与实际运行状态等级对比,精度达到96.2%,而随机森林评价模型精度为93.6%.验证了本文所提运行评价方法的有效性.

图2 运行状态等级概率Fig.2 Probability of grade of running state

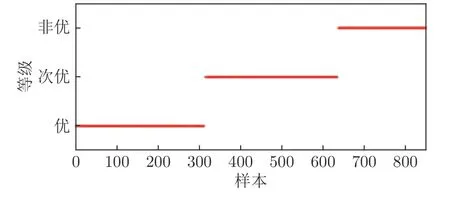
图3 运行状态评价等级Fig.3 Grade of running state

两种算法的对比实验结果如表3所示.从表3可以看出与传统的随机森林算法相比,本文所提改进算法的决策树数量大大减少,且改进算法在一定程度上提高了评价精度.

表3 RF 与MIWRF 实验结果对比Table 3 Comparison of experimental results of RF and MIWRF

为了进一步验证所提方法的评价性能,将MIWRF 方法与KNN(K near neighbor),ANN(Artificial neural network),RF(Random forest),基于互信息精减决策树但未加权的随机森林算法MIRF(Mutual information random forest)和文献[2]中的FDbD 方法进行了对比实验.KNN 中,近邻数设置为10 并采用曼哈顿距离.ANN 中,神经网络的层数为2,隐含层神经元个数为10.RF、MIRF、MIWRF 的参数设置与第3.3 节一致.FDbD 是基于Dempster-Shafer 理论的模糊动态因果图方法,该方法应用模糊理论减少了定量变量离散化导致的信息损失,同时针对DCD(Dynamic causal diagram)中取值/状态既能通过原因节点进行推理又能被测量/估计的节点,通过DST 先将多源信息进行融合,再进行推理,弥补了传统DCD 无法同时利用推理和测量估计所提供的信息的缺陷.

表4 列出了6 种算法的运行结果,包括评价精度、建模时间和测试时间,可以看出,通过对决策树的精简和加权投票,可以得到最佳的运行状态评价结果.与传统的评价方法(KNN,ANN)相比,基于随机森林的评价方法在精度上有了显著的提高,这表明基于集成学习的评价方法比单一模型的评价方法具有更好的性能.对于3 种基于随机森林的运行评价方法,传统的随机森林建模时间相对较长,主要是因为RF 的训练集比MIRF 和MIWRF 大,不需要从训练集中划分出验证集.但RF 的评价精度比MIRF 和MIWRF 低,这主要是因为RF 的决策树存在冗余且部分精度较低,而基于互信息分组选择后的决策树具有多样性且精度高.高精度和多样性的基学习器能提高集成学习器的泛化能力.与MIRF 相比,MIWRF 对于运行状态的精度进一步提高但训练时间与测试时间略长,这是由于MIWRF 算法对决策树输出结果进行了加权,强化了性能好的决策树同时弱化了性能差的决策树.与FDbD 方法相比,MIWRF 的精度有一定的提升且在时间上有微弱的优势.FDbD 基于过程知识和数据建立运行评价模型,在评价模型中引入过程知识一方面充分利用了过程知识,另一方面增强了模型的解释性,这些优点在非优原因追溯阶段得到了充分的体现,基于FDbD 模型追溯的非优原因更接近引起非优运行状态的根本原因.但在实际应用中过程知识的提取相对困难且所获得的过程知识难以保证完备,同时加入过程知识的评价模型难以推广到一般的工业过程.MIWRF 完全基于数据,能轻易推广到一般的工业过程,但如何基于MIWRF 进行非优原因追溯有待进一步研究.综上所述,MIWRF不仅降低了评价模型的复杂度,还提高了评价模型的精度.

表4 6 种评价方法的运行状态评价性能Table 4 Performances of 6 evaluation methods

3.5 实际数据测试

为了进一步验证本文方法的实用性,从某冶金厂获取5 组现场数据用于仿真验证,5 组数据的运行状态评价评价结果如图4～8所示,评价精度达96.1%,能够满足定量信息与定性信息共存的复杂工业过程的运行状态评价要求.说明本文所提方法在现场实际生产过程中具有应用价值.

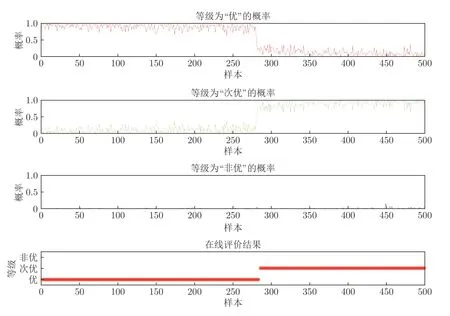
图4 优到次优的转换Fig.4 Transformation from optimal to suboptimal

4 结束语

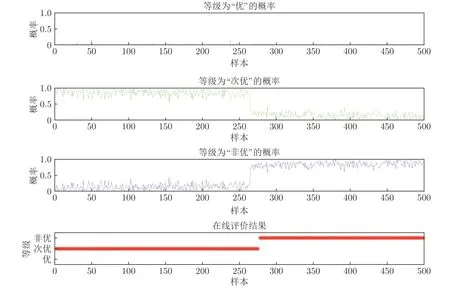
图5 次优到非优的转换Fig.5 Transformation from suboptimal to non-optimal

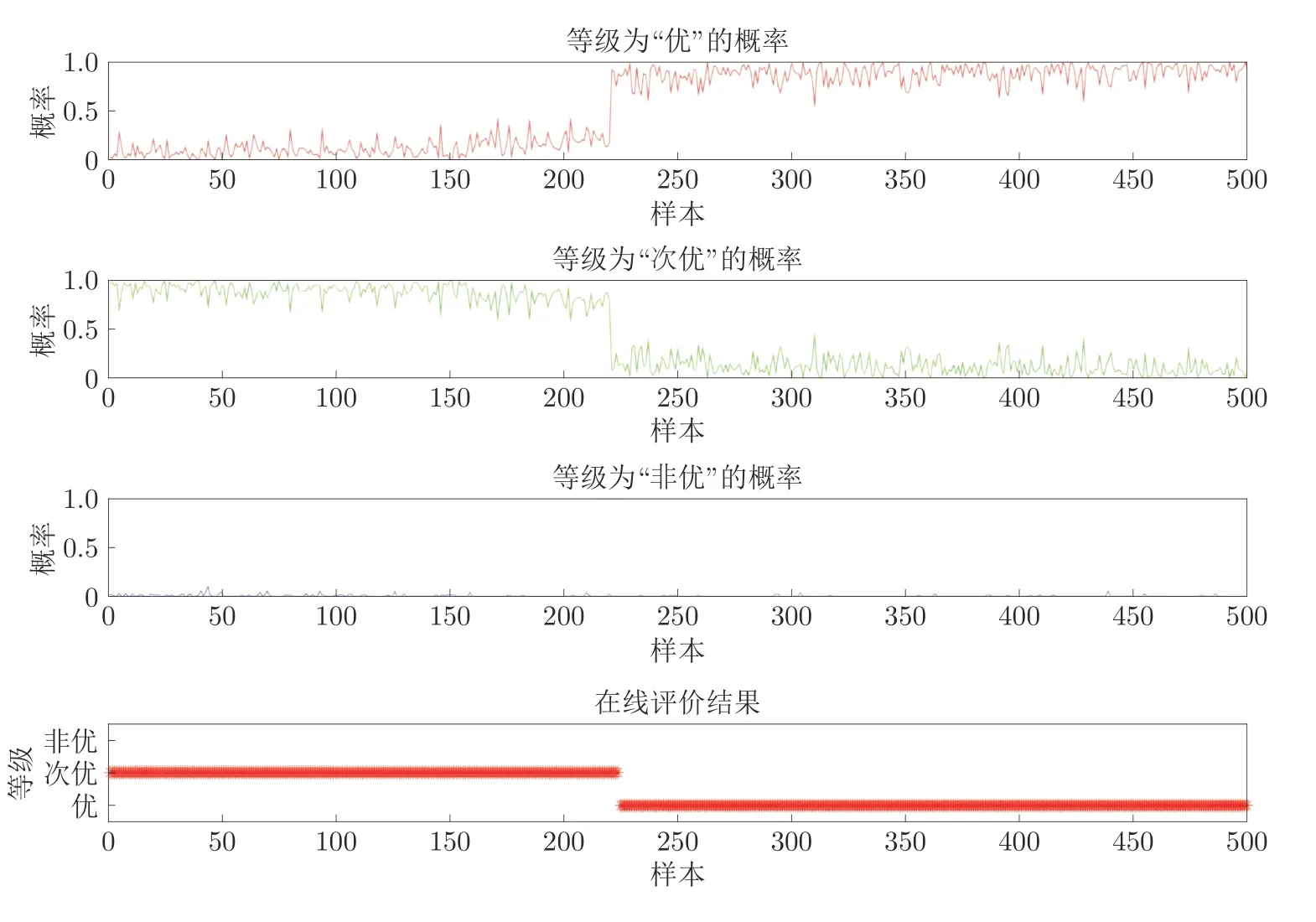
图6 次优到优的转换Fig.6 Transformation from suboptimal to optimal

本文针对定量信息与定性信息共存的工业生产过程的运行状态评价问题,提出了基于互信息的改进随机森林方法,并且建立了运行状态评价模型以及相应的在线评价策略.解决了定量与定性信息共存下的运行状态评价问题,与传统随机森林方法相比,不但提高了运行状态评价的精度,而且降低了模型的复杂度.将本文所提出的方法与传统运行评价方法进行了对比仿真实验并应用于湿法冶金氰化浸出过程,仿真和实际应用结果证明了所提方法的正确性与有效性.

图7 非优到次优的转换Fig.7 Transformation from non-optimal to suboptimal

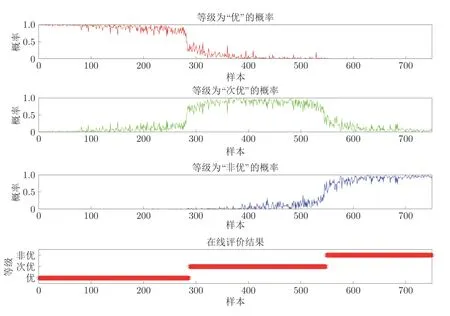
图8 优、次优到非优的转换Fig.8 Transformation from optimal,suboptimal to non-optimal

此外,在对上述工作进行研究时,本文并未考虑如何采取有效措施进行非优运行状态原因追溯.即当运行状态评价结果为非优时,通过非优原因追溯,追溯出导致非优的变量,并结合过程特性给出操作指导建议.未来的研究将会围绕如何基于随机森林进行非优原因追溯展开.

综上所述,本文针对复杂工业过程提出的运行状态评价方法,在现有成熟方法上进行改进和应用,具有科研价值,但仍存在研究空间.