基于FFT 功率谱和SVD 的局放窄带干扰降噪方法研究

袁玉昌，杨 姚，袁 庚，苏旭磊，尹豪杰，张梦楠

0 引言

局部放电检测作为一种可以有效检测电缆终端绝缘状态的方法，能够反映出电缆终端故障的严重程度并判断出故障类型[1]。然而，牵引变电所电缆终端在局部放电检测的过程中往往会受到现场复杂环境的干扰，包括交通噪声以及其他常见环境干扰等。电缆终端局放测试中的干扰主要分为以下3 种[2]：周期性窄带干扰、随机性脉冲干扰和白噪声干扰。其中，周期性窄带干扰主要来源于电网络内部及环境中的无线电广播等，其出现频率高，幅值大，常在时域内将局放信号湮没，且在频域范围内经常与局放信号混叠，对局放信号的检测影响较大。因此，对于周期性窄带干扰的抑制至关重要。目前针对窄带干扰的抑制方法，国内外学者已经进行了大量研究，主要有傅里叶分析[3]（Fast Fourier Transform，FFT）、小波包变换[4]等方法。针对傅里叶分析，文献[5]利用PD 信号与窄带干扰信号频窗能量比的不同，提出通过能量比对FFT功率谱预处理，再通过阈值对能量比进行处理，但该方法存在不同的染噪信号阈值选取难以自适应以及频窗选取存在误差的问题。文献[6]在此基础上提出采用局部能量比法，并使用模糊C-均值对局部能量比进行聚类，从而实现窄带干扰的自适应阈值选取，有效解决了上述问题，但其获取的PD信号发生了一定程度衰减和畸变。针对小波包变换法，文献[7]提出结合实小波包幅频特性和复小波相频特性的复小波变换法抑制窄带干扰，但当窄带干扰频率与PD 信号存在混叠时，去噪效果不理想。文献[8]基于频率切片小波变换自由分割时频面的优点，提出一种频率切片小波变换时频分析新方法，但存在信号能量衰减和信号畸变的问题。

除了以上噪声抑制方法，奇异值分解[9，10]（Singular Value Decomposition，SVD）也是一种有效的噪声抑制方法。文献[11]对含有单一频率窄带干扰的PD 信号进行SVD 分解，发现通过提取前两个奇异值可有效提取窄带干扰信号，但文中仅添加一个频率窄带干扰信号，对奇异值的数量与窄带干扰频率个数之间的关系没有参考价值。文献[12]针对信号有效奇异值选取问题，发现有效奇异值的数量由信号中窄带干扰频率个数决定，即每个频率的窄带干扰均对应两个非0 奇异值，但其并未给出窄带干扰频率个数的确定方法。文献[13]提出基于Hankel 矩阵和奇异值分解的窄带干扰去噪方法，并提出利用K 均值算法找出窄带干扰对应奇异值并滤除，但存在窄带干扰信号幅值相对较小时会导致窄带干扰对应的奇异值数值选取偏少而造成去噪不彻底的问题。

针对上述局放信号周期性窄带干扰抑制存在的问题，本文提出基于FFT 功率谱的奇异值分解降噪方法。通过对染噪PD 信号获取功率谱，利用改进的阈值法初步判断窄带干扰个数n，并选取前2n个奇异值进行窄带干扰的重构；随后对剩余奇异值两两成对依次进行重构，当首次出现重构信号不满足正（余）弦规律时，停止奇异值重构，并确定重构信号满足正（余）弦规律所对应的奇异值即为对应的窄带干扰；通过将两次重构得到的窄带干扰信号从染噪局放信号中去除，即可获得不含窄带干扰的染噪局放信号。

1 奇异值分解

1.1 Hankel 矩阵

本文选取Hankel 矩阵作为奇异值分解的轨迹矩阵。Hankel 矩阵具体构建方式如下：

设染噪信号X为

式中：m+n- 1 =N，n取N/2。

1.2 奇异值分解原理

设A是一个m×n的矩阵，矩阵的秩为r，则必存在m×n的正交矩阵U和正交矩阵V，使得

对角矩阵Λ除了前r阶对角元素外，其他元素均为零。对角元素∂i（i= 1,2,…,r）即为矩阵A的奇异值，且数值由大到小排列。奇异值的大小反映了能量的集中情况，较大的奇异值反映了局放信号成分，而较小的奇异值则反映了信号噪声。通过选取合适的奇异值阈值，将较小的奇异值滤除即可实现噪声的抑制，还原真实的局放信号。

1.3 仿真信号分析

通过对现场电缆终端局放信号的检测和参考大量文献，发现电缆终端局放信号通常表现为振荡衰减的形式。本文选取单指数振荡衰减和双指数振荡衰减两种衰减模型[14]来模拟理想局放信号。具体表达式如下：

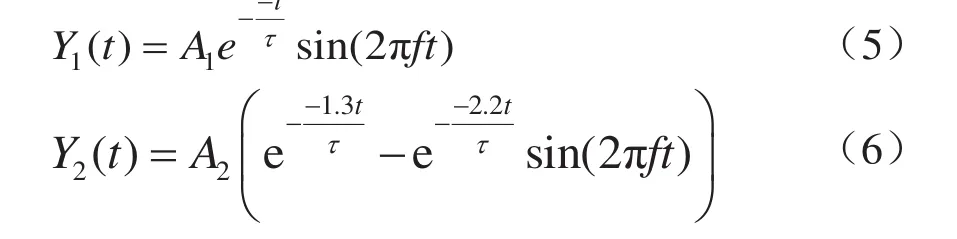
式中：f为振荡频率；τ为衰减系数；A1、A2均为脉冲幅值。

为验证仿真结果的有效性，设置2 组单指数振荡衰减模型和2组双指数振荡衰减模型模拟4种局放信号脉冲。仿真参数如表1 所示。

表1 局放仿真信号参数

周期性窄带干扰信号通常呈正弦波或余弦波波形[15]，本文选取窄带干扰频率fi为f1= 0.5 MHz，f2= 1 MHz，f3= 3 MHz，f4= 5 MHz，f5= 7 MHz。周期性窄带干扰的具体表达式为

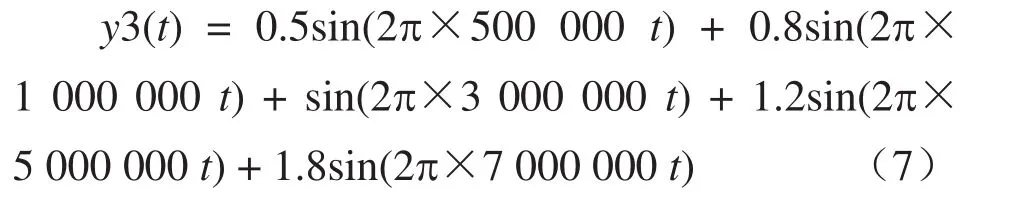
考虑到现场检测时会受到白噪声干扰，故为局放信号叠加分布为(0，10)的高斯白噪声。仿真中设置采样率为25 MHz/s，采样时间为40 μs，得到理想PD 仿真信号如图1（a）所示，添加周期性窄带干扰和白噪声后的信号如图1（b）所示。

图1 仿真波形

1.4 窄带干扰奇异值特征分析

对式（7）周期性窄带干扰信号进行奇异值分解得到对应的奇异值信息如图2 所示。从图中可以看出，前2×5 = 10 个奇异值较大，后面的奇异值几乎为零。因此，通过提取前10 个奇异值信号即可反映出窄带干扰几乎全部的信息。

图2 窄带干扰奇异值

图3 为沾染窄带干扰和白噪声信号的奇异值系列图。f1(t)对应纯窄带干扰信号奇异值，f2(t)对应染噪PD信号奇异值，f3(t)对应原始PD信号奇异值。从图中可以看出，染噪信号的前10 个奇异值与纯窄带干扰信号保持一致，对应的奇异值较大，而后面的奇异值与不加窄带干扰的PD 信号保持一致，奇异值相比前10 个奇异值信号普遍降低。通过增减窄带干扰频率个数k，发现信号对应的前2k个奇异值较大，并且与纯窄带干扰信号对应的奇异值保持一致。由此，验证了文献[16]中关于周期信号有效奇异值数量为信号频率个数的两倍的结论。

图3 窄带干扰+白噪声PD 信号奇异值

2 FFT 功率谱

染噪信号FFT 频域谱计算式如下：

设信号x(t)的频域变换为X(ω)，则有

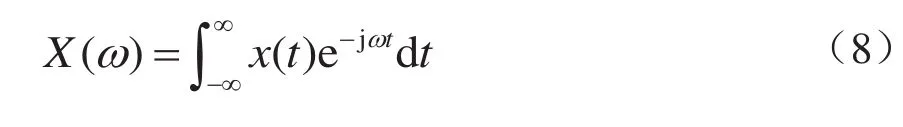
对应FFT 功率谱P(ω)为

理想局放仿真信号和染噪局放信号功率谱如图4 所示。

图4 仿真信号功率谱

从图中可以看出，窄带干扰在功率谱中表现为强度明显大于局放信号的干扰峰。利用该特点即可确定窄带干扰的数量。为自适应确定窄带干扰的个数，引入经典阈值法[16]。经典阈值法表达式为

式中：σ、N分别为信号的标准差和采样点数。

经研究发现，使用阈值T确定窄带干扰数量通常导致幅值相对较小的窄带干扰被排除，从而导致窄带干扰滤除不彻底。为解决该问题，引入调节因子λ（λ取值为0.5～1，本文取0.8），改进的阈值表达式为

对染噪局放信号功率谱采用改进的阈值法挑选出窄带干扰个数。从图4(b)中可以看出，当窄带干扰对应幅值较小时，仍存在部分窄带干扰被忽略。因此，有必要对窄带干扰进行进一步滤除。

3 周期性窄带干扰抑制方法

从上述采用FFT 功率谱对染噪局放信号进行阈值处理确定窄带干扰个数的结果发现，幅值较小的窄带干扰未被提取。因此，本文提出基于频率谱的奇异值分解降噪方法，可有效提高窄带干扰个数确定的精度。窄带干扰抑制方法具体步骤如下：

（1）对染噪局放信号进行功率谱计算，结合改进的阈值法初步确定窄带干扰个数；

（2）提取窄带干扰对应的奇异值进行重构，获取部分窄带干扰信号；

（3）对剩余奇异值两两成对依次进行重构，判断重构信号是否符合正（余）弦规律，当首次出现重构信号不符合正（余）弦规律时，停止重构；

（4）将利用功率谱得到的重构信号和利用剩余奇异值重构获取的符合正（余）弦规律的信号进行叠加，即为染噪局放信号中所含有的全部窄带干扰信号；

（5）利用原始染噪局放信号减去重构后的窄带干扰信号，即可获取仅含白噪声的局放信号。

4 去噪效果对比

为分析本文所述改进的奇异值分解的周期性窄带干扰抑制方法的去噪效果，对原始局放仿真信号加入周期性窄带干扰进行去噪处理。通过引入FFT 阈值去噪、小波去噪和EMD-小波变换联合去噪方法与本文所述方法进行对比，各方法去噪结果如图5 所示。对比各类方法去噪结果得出：FFT 阈值去噪法能有效滤除周期性窄带干扰信号，但抑制效果不够理想，存在残余噪声且信号失真严重；小波去噪无法将含噪信号进行有效分离，去噪后仍无法判断PD 信号分布情况。

图5 去噪结果

为准确判断各去噪方法的去噪效果，需要引入去噪评价参数[17]对去噪效果进行评估，从而定量判断去噪效果。本文选用信噪比（signal to noise ratio，SNR）、均方误差（mean square error，MSE）和波形相似参数（normalized correlation coefficient，NCC）对去噪效果进行评估。

对各类去噪方法的评估结果如表2 所示。从表中可以看出，本文所述方法具有明显的优势，无论从信噪比、均方误差还是波形相似参数方面均表现出非常良好的效果，对于窄带干扰的抑制效果最好，且信号畸变非常小。

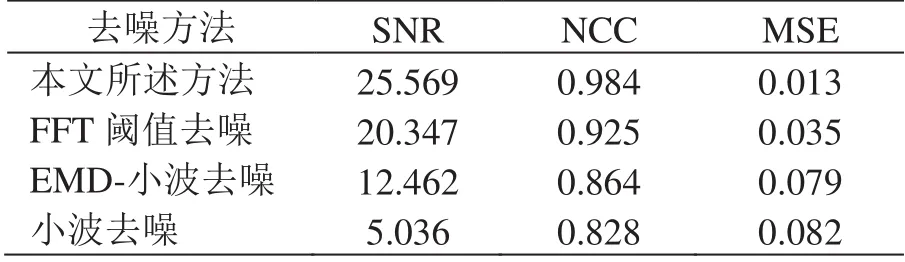
表2 周期性窄带干扰特征参数计算结果

5 实测信号去噪分析

为检验本文所述方法对于实测信号滤除周期性窄带干扰的能力，基于实验室条件下测试乙丙橡胶沿面放电缺陷模型，得到PD 信号波形如图6（a）所示。由于是基于比较理想的实验室条件下进行测试，故而PD 信号明显，且环境噪声干扰小。为测试本文所述窄带干扰去噪方法对实测信号的去噪效果，对实测PD 信号施加5 个不同频率和幅值的周期性窄带干扰信号，染噪信号如图6（b）所示，去噪结果如图6（c）所示。

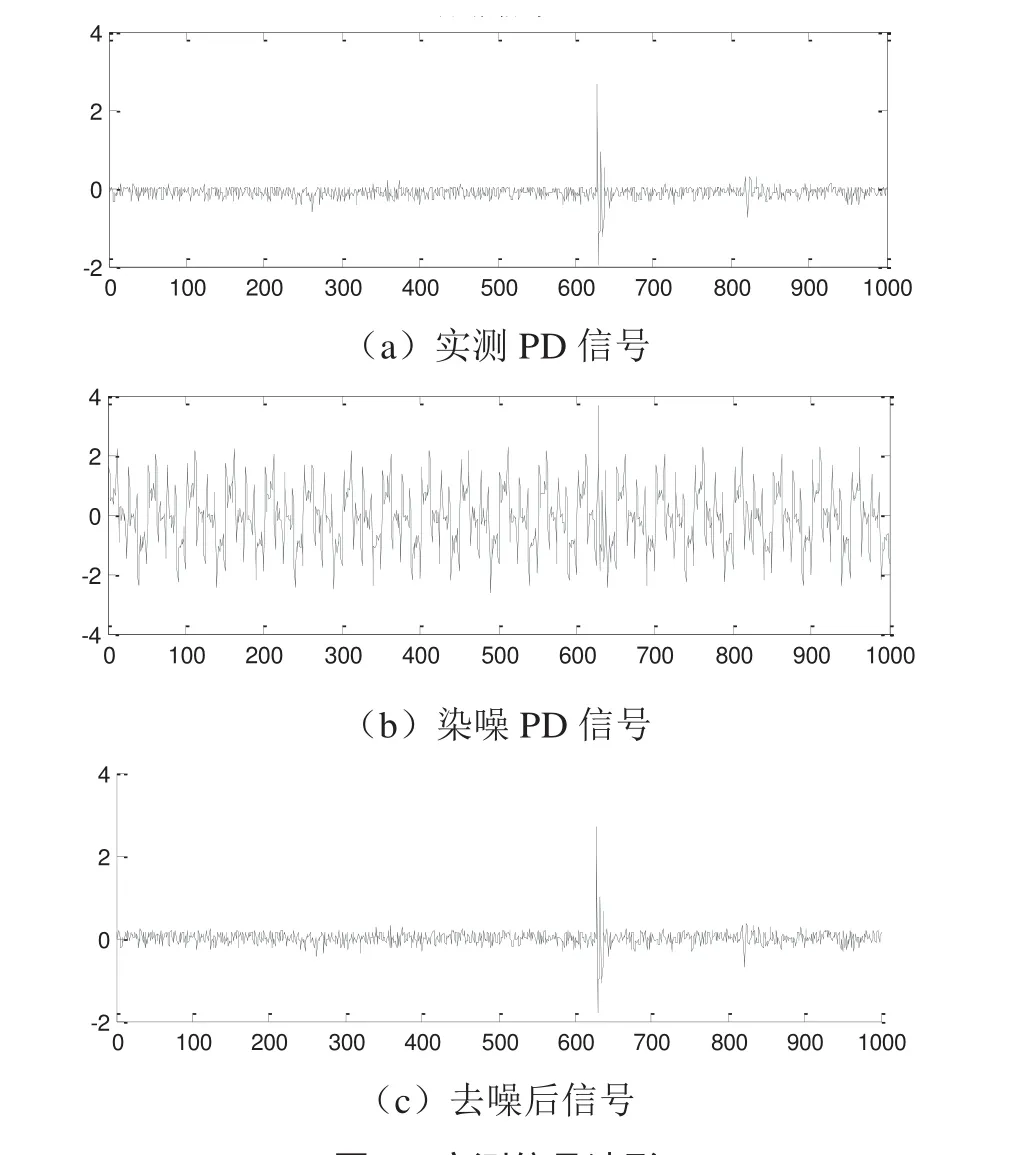
图6 实测信号波形

从图中可以很明显地看出，采用本文所述去噪方法能够高度还原原始PD 信号，且抑制噪声效果较好。

6 结论

本文提出一种基于奇异值分解的电缆终端局放信号窄带干扰降噪方法，通过与FFT 阈值去噪、小波去噪等方法相比较，并分析降噪结果，得出以下结论：

（1）基于Hankel 矩阵的信号奇异值分解中，窄带干扰的频率个数对应于信号奇异值个数的两倍，且对应的奇异值仅与窄带干扰有关，与PD 信号无关，故而通过窄带干扰对应的奇异值进行信号重构时，不会导致PD 信号衰减；

（2）通过将信号进行功率谱计算并结合改进的阈值法初步确定窄带个数，可有效提高窄带干扰个数提取的准确率；

（3）将剩余的奇异值依次两两成对进行重构，通过判断其是否符合正弦或余弦规律，较彻底提取出染噪信号中存在的窄带干扰；

（4）通过与FFT 阈值去噪和小波去噪方法进行对比，发现本文所述方法能更好地抑制窄带干扰信号，高度还原PD 信号，使其受衰减影响较小。