滚石冲击结构物动力响应特征数值模拟研究

吴东东，温继伟，项 天，张 杰，肖 烽

（成都理工大学环境与土木工程学院，四川成都610059）

0 引言

我国疆域辽阔，地形多样，其中山地面积约占总面积的2/3，众多的山区地形孕育了大量的地质灾害，如滚石、崩塌、滑坡、泥石流等。尤其在我国的西南地区，自2008年5月12日汶川地震后加剧了山体破碎，孤石遍布，诱发了大规模的滚石地质灾害，导致部分房屋、车辆被损毁，道路、桥梁等基础设施被破坏，交通干道被迫中断，给人民生命财产、基础设施运营等造成了严重的损失和安全隐患［1-2］，如图1所示。因此，对于滚石灾害防护已成为保障人民生命财产、基础设施顺利建设与运营安全亟需解决的难题。

图1 典型滚石冲切破坏建（构）筑物地质灾害[2]Fig.1 Typical geohazards of rockfalls impact where buildings or str uctur es wer e destr oyed

当前，关于滚石地质灾害的主要研究方法包括理论研究、物理模型试验、现场原位试验及数值模拟研究。其中，理论研究虽能描述滚石运动前后速度及能量的变化，但是难以预测滚石运动轨迹；物理模型试验因存在缩尺效应，不能完全重现滚石灾害过程，因而与实际相比存在较大误差；现场原位试验由于成本高、周期长，因此很少有人开展现场原位试验研究；数值模拟成本低、时间短，可模拟复杂工况，作为试验的补充手段，备受科研工作者的青睐。

何思明等［3］以弹塑性接触理论为基础，研究了滚石法向回弹系数与切向回弹系数的计算方法，运用运动学基本方程，研究了滚石在坡面上的运动特征，并推导出相关计算公式。叶四桥等［4］通过模型试验，研究了滚石运动过程中法向恢复系数对滚石运动路径的影响。黄润秋等［5］开展了滚石运动特征试验，分析了坡面特征对滚石停留位置的影响，以及坡面对滚石运动时间和对不同形状滚石的运动特性的影响，为危岩体防治时冲击能量的确定提供了依据。裴向军等［6］采用动力有限元方法对滚石冲击砂土垫层进行了数值仿真计算，分析了不同冲击能量下多组砂土垫层厚度组合的动力响应及耗能缓冲机理，为滚石多发区棚洞结构砂土垫层的设计提供了理论依据。王东坡等［7-8］通过静力压痕数值实验获取了不同垫层结构与滚石在加卸载条件下的接触力-压痕关系，并将其引入棚洞板的冲击动力控制方程中，进而计算滚石冲击荷载下不同垫层结构棚洞板的动力响应，并与动力有限元结果进行了对比分析。王静峰等［9］基于室外大尺度模型实验，建立了落石冲击作用下EPS（Expanded Polystyrene，聚苯乙烯泡沫板）复合垫层钢棚洞结构的数值计算模型，研究了复合垫层对落石冲击的缓冲效果。

滚石防护主要可分为主动防护与被动防护，但由于山区地形条件限制，主动防护往往难以实施，故工程上常采用棚洞、拦石墙和帘式网等被动防护措施来减轻或避免滚石灾害对灾害易发区沿线公路、铁路等构筑物造成损害。许多学者针对不同的防护结构开展了试验研究，Kishi N.等［10］通过原位试验研究了2种类型的混凝土棚洞在滚石冲击下的极限抗冲击能力。Lambert S.等［11］通过试验研究了在拦石墙前放置填充有碎石的宾格石笼，在滚石冲击下其填料和边界对土工格室的影响。Buzzi O.等［12］通过室内试验研究了在低能级冲击下帘式网的刚度及系统的耗能效果。Peila D.等［13］以重达9000 kg的混凝土块以大约30 m/s的速度冲击土工格栅加筋土拦石墙，研究由不同土工格栅类型和不同尺寸的拦石墙在不同的冲击能量条件下的动力响应，从而对这些结构的抗冲击能力进行定量评估。OUY⁃ANG Chaojun等［14］采用有限元方法对落石冲击的瞬态动力学过程进行了计算分析，研究了土工格栅加筋土与聚苯乙烯泡沫塑料结合的棚洞防护体系的抗冲击性能。

现有研究大多是对滚石冲击结构物机理的探究，但对于滚石形状和受冲击结构物形状对滚石冲击过程的影响方面的研究相对较少。本文将滚石和结构物表面分别设置为4种不同的形状，采用数值模拟研究方法探究滚石冲击结构物过程，并对比分析不同缓冲层对滚石冲击的耗能效果。

1 滚石运动过程与数值模型建立

1.1 滚石运动过程

滚石是指各种石块因某种原因从地质体表面失稳脱落后经下落、回弹、跳跃、滚动或滑动等运动方式中的一种或几种的组合沿着坡面向下快速运动，最后在较平缓的地带或障碍物附近停止下来的一个动力演化过程［1-5］，如图2所示。

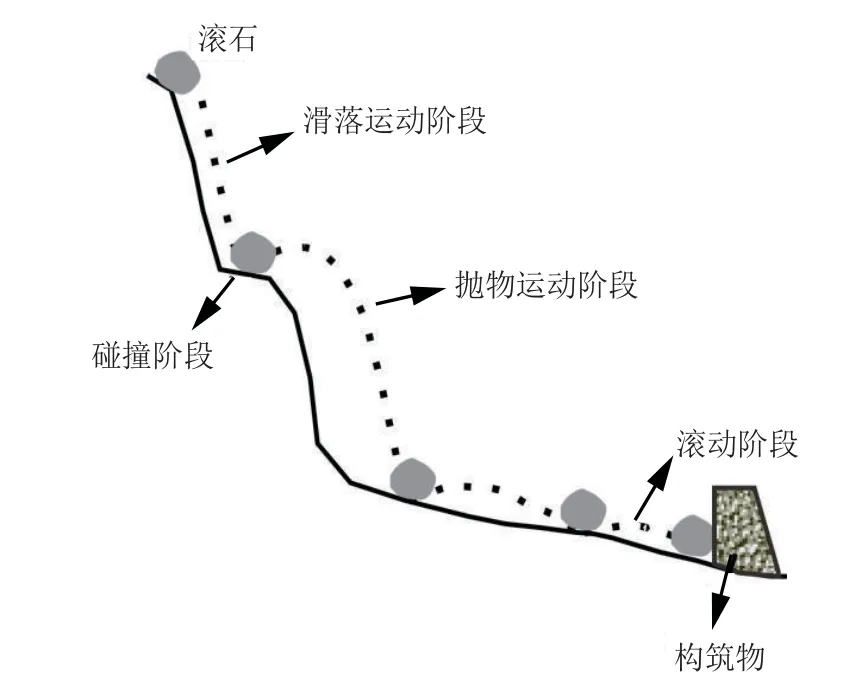
图2 滚石运动示意Fig.2 Schematic diagram of rockfall movement

由图2可以看出，滚石在运动过程中主要是将重力势能转化为动能，但是由于滚石在运动过程中会与坡体表面发生碰撞或沿坡体表面滑动会消耗部分能量，根据能量守恒原理，当滚石冲击构筑物时，其冲击能量将小于初始能量。本文主要运用有限元数值模拟方法对滚石冲击构筑物瞬态过程展开研究。

1.2 数值模型建立

本文采用ABAQUS有限元软件中的Explicit动力有限元方法进行数值模拟计算。由于滚石形状具有不确定性，不同形状的滚石对结构物的冲击响应特征差异较大。因此，本文研究的对象是不同形状的滚石对平面墙状构筑物的冲击动力响应特征，所以建立了如图3所示的4种不同形状的滚石模型，分别为正方体、圆柱体、球体和三棱锥；同时，建立的平面墙状构筑物模型的尺寸为2 m×2 m×0.5 m，为保证4种不同形状滚石的体积一致，经计算，在建模时正方体滚石模型的边长设为0.2 m，球体滚石模型的半径设为0.124 m，圆柱滚石模型底面圆的半径和高分别设为0.113 m和0.2 m；三棱锥滚石模型底面等边三角形的边长和高分别设为0.525 m和0.2 m。

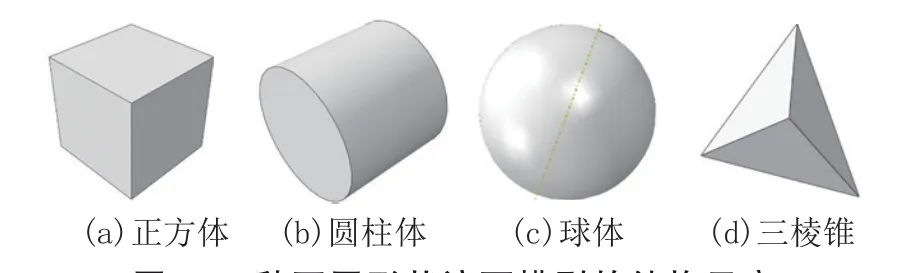
图3 4种不同形状滚石模型的结构示意Fig.3 Modeled structures of four different shaped rockfalls

本文的另一研究对象是同一形状滚石对具有不同表面形状结构物的冲击响应特征，设置了如图4所示的4种具有不同表面的结构物，即：波浪状、斜面状、凹面状及凸面状的结构物。

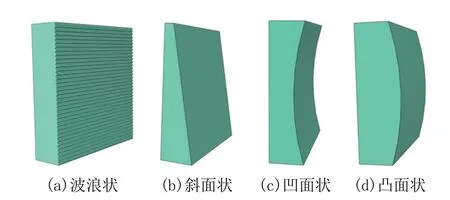
图4 4种不同表面形状结构物示意Fig.4 Schematic diagram of four structures with different sur face shapes

当不同形状的滚石冲击不同表面的结构物时，它们之间相互接触的工况条件也不同。如图5所示，以不同形状的滚石冲击平面墙状结构物为例，当正方体滚石冲击平面墙状结构物时，它们之间相互接触的工况条件为“正方形平面-平面”；当球体滚石冲击平面墙状结构物时，它们之间相互接触的工况条件为“半球面-平面”；当三棱锥滚石冲击平面墙状结构物时，它们之间相互接触的工况条件为“锥尖面-平面”；当圆柱滚石的底面冲击平面墙状结构物时，它们之间相互接触的工况条件为“圆形平面-平面”；当圆柱滚石的侧面冲击平面墙状结构物时，它们之间相互接触的工况条件为“半圆柱面-平面”。

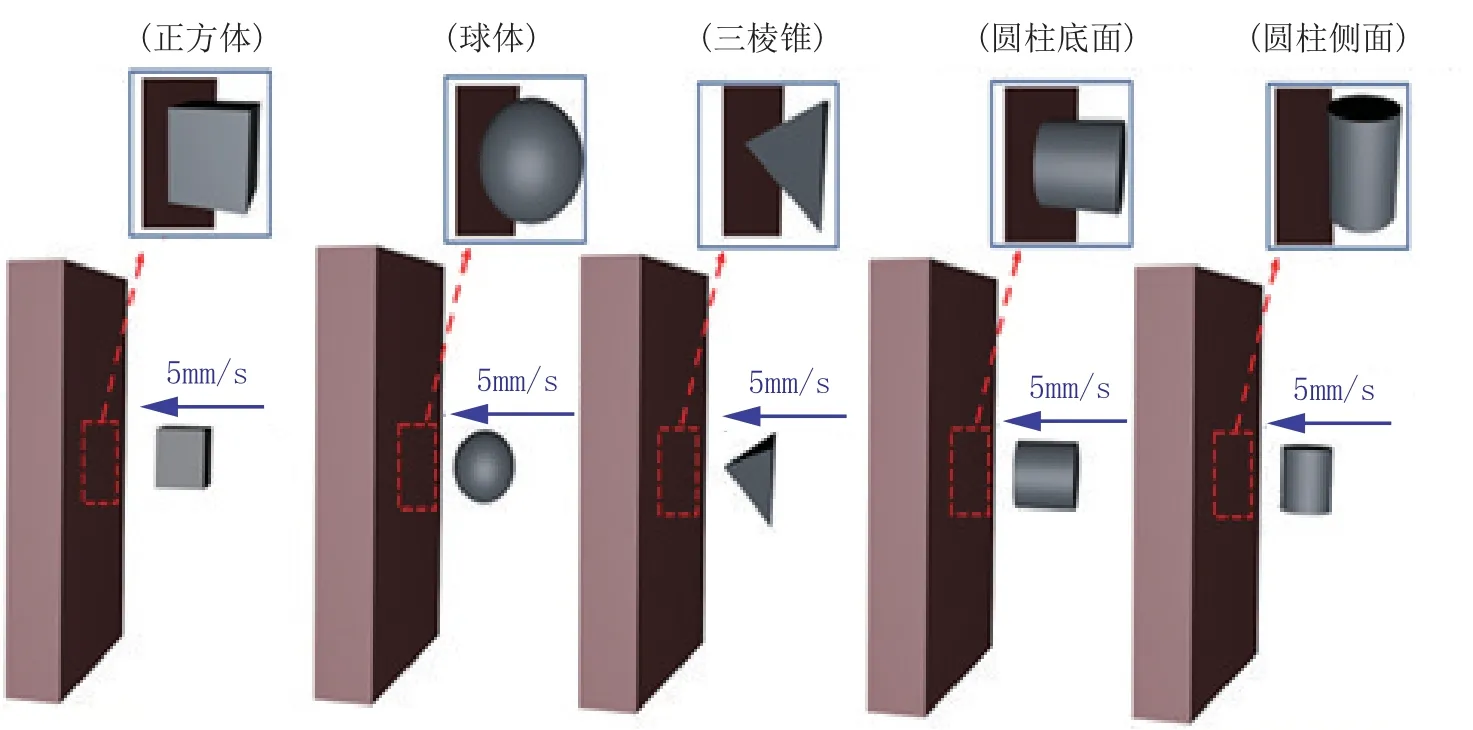
图5 不同滚石冲击构筑物原理Fig.5 Schematic diagr am of impact of str uctur es by differ ent r ockfalls

此外，为探究不同缓冲层对滚石冲击的缓冲耗能效果，建立了如图6所示的数值计算模型，图6（b）为在平面墙状结构物前增设了厚度为0.3 m的缓冲层。将滚石约束成刚体并施加5 m/s的水平初速度，固定结构物底面，并对缓冲层底面进行位移约束，滚石、缓冲层和结构物之间相互作用类型为表面与表面接触。结构物均设为混凝土材质，采用Con⁃crete Dameged Plasticity模型；缓冲层分别设为砂土、泡沫铝、EPS三种材质，其中砂土采用Drucker-Prager模型，泡沫铝和EPS采用Crushable Foam模型；混凝土、EPS、砂土的本构模型可参见文献［15］，泡沫铝本构模型可参见文献［16］、［17］。表1为本文数值模拟研究各种材料的物理力学参数。

图6 滚石冲击结构物的数值计算模型Fig.6 Numerical calculation model of the structures impacted by rockfalls

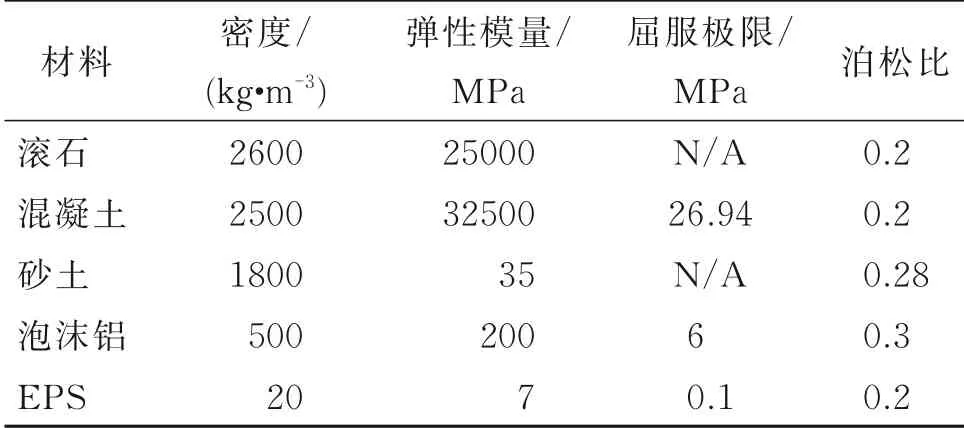
表1 材料物理力学参数[15-17]Table 1 Physical and mechanical par ameters of materials

2 不同形状滚石冲击平面墙状结构物分析

2.1 滚石冲击力分析

图7为不同形状滚石冲击平面墙状结构物的冲击时程曲线，从图中可以看出，5种工况下的冲击力时程曲线差异较大；当滚石形状为正方体和圆柱体（底面）冲击平面墙状构筑物时，冲击力较其它工况更大，冲击力峰值分别达到了1432.41、1089.47 k N；当滚石形状为圆柱体（侧面）冲击平面墙状构筑物时，冲击力峰值为299.16 k N，但是相比于正方体和圆柱体滚石，其冲击力峰值大幅减小；当滚石形状为球体冲击平面墙状构筑物时，冲击力较圆柱体（侧面）时减小了5.2%，冲击力峰值为283.66 k N；当滚石形状为三棱锥冲击平面墙状构筑物时，冲击力峰值仅为124.79 kN，较球体时减小了56.01%，是上述5种形状滚石中冲击力最小的。因此，在滚石地质灾害中，滚石形状对结构物冲击力的影响较大。在本文研究的滚石形状中，冲击力峰值大小依次是正方体＞圆柱体（底面）＞圆柱体（侧面）＞球体＞三棱锥。产生这一现象的机理主要是：由于设置滚石的冲击速度和质量不变，当不同形状的滚石以同一速度冲击相同结构物时，其冲击力主要受结构物与滚石冲击时接触面积影响，当不同形状的滚石冲击平面墙状结构物时，它们之间的接触面积越大则相应的冲击力越大，有效冲击时长越短，冲击力时程曲线越尖锐，反之亦然，这与参考文献［18］中得出的结论基本一致。

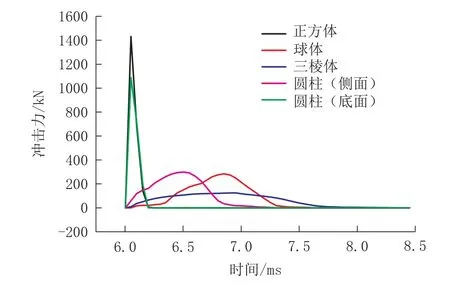
图7 不同形状滚石的冲击力时程曲线Fig.7 Time histor y curve of impact for ce of the rockfalls with various shapes

2.2 结构物位移变形分析

以结构物中心受滚石冲击后的单元位移变形情况来表征其承受滚石冲击点的破坏程度。图8为上述不同工况的结构物中心承受滚石冲击时的单元位移变形时程曲线，从图中可以看出，各工况下的位移变形时程曲线都有上升、下降、趋于稳定3个阶段，符合经典弹塑性理论的基本解释，滚石冲击结构物过程主要由2部分组成，分别是典型弹塑性压入阶段和卸荷回弹阶段，在典型弹塑性压入阶段又可分为弹性压入阶段和塑性压入阶段。不同工况下所达到最大位移的时间与达到冲击力峰值的时间基本一致。不同形状滚石对平面墙状结构物中心受冲击时的单元位移变形量大小依次是三棱锥＞球体＞圆柱体（侧面）＞正方体＞圆柱体（底面），其最大位移变形量分别为2.93、2.81、1.09、0.13及0.12 mm。因此，“锥尖面-平面”的冲击方式对结构物中心受滚石冲击时的单元位移变形影响最大；其次是“半球面-平面”的冲击方式，相比前者，其位移变形量减小了4.1%；而后是“半圆柱面-平面”的冲击方式，其单元位移变形量较前两者大幅减小，相对于“半球面-平面”的冲击方式减小了61.2%；“平面-平面”的冲击方式是单元位移变形量最小的工况，且圆柱体（底面）滚石冲击的位移变形时程曲线与正方体滚石冲击的位移变形时程曲线几乎重合，且近乎为2条“水平线”，其最大位移变形量远小于其它工况。基于此，滚石的形状对滚石冲击平面墙状结构物中心时的单元位移变形量有较大影响，表现为当滚石冲击面形状越尖锐，则结构物受滚石冲击处的位移变形量越大（结构物越易被破坏），当滚石形状由“尖”变“钝”时，结构物受滚石冲击处的位移变形量越小（结构物越不易被破坏）。

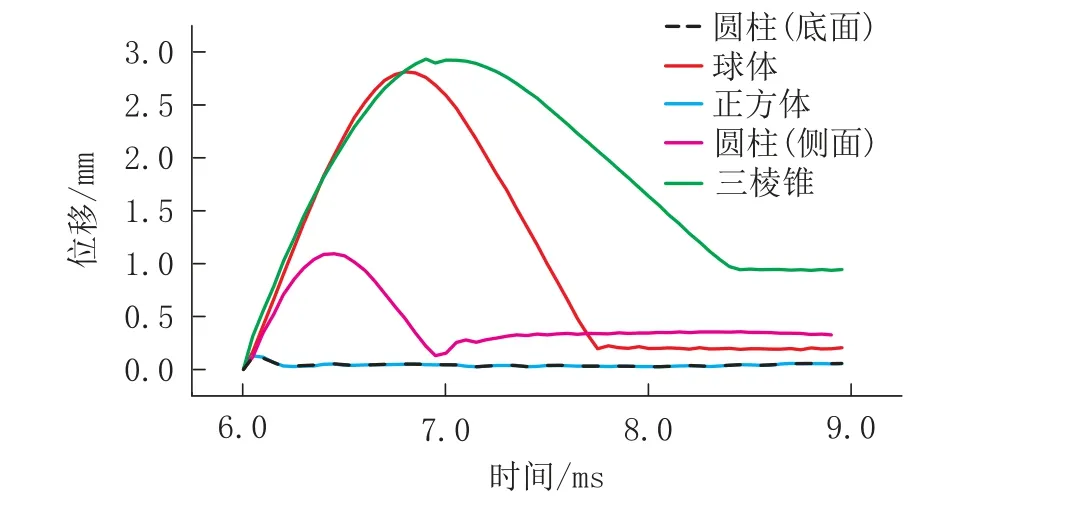
图8 结构物承受不同滚石冲击的单元位移变形时程曲线Fig.8 Time history curve of the unit displacement of the structur es impacted by various r ockfalls

为了更加清晰地观察、对比分析不同形状滚石冲击结构物中部位置时的动力响应特征，将各模型进行中心剖分，相应的模型位移云图如图9所示，不难看出，当滚石冲击方式为“平面-平面”时（图9a、图9d），结构物中心处的整体变形区域（绿色区域）更大，而当滚石冲击方式为“锥尖面-平面”时（图9c），结构物中心处的整体变形区域最小，而其它2种工况时（图9b、图9e）结构物中心处的整体变形区域大体一致，且介于上述2种工况之间。因此，滚石的形状对结构物冲击变形的范围也有较大的影响，总体表现为当滚石冲击面形状越“钝”，则结构物内部产生的变形区域越大，当冲击面形状越“尖”，则结构物内部产生的变形区域越小。

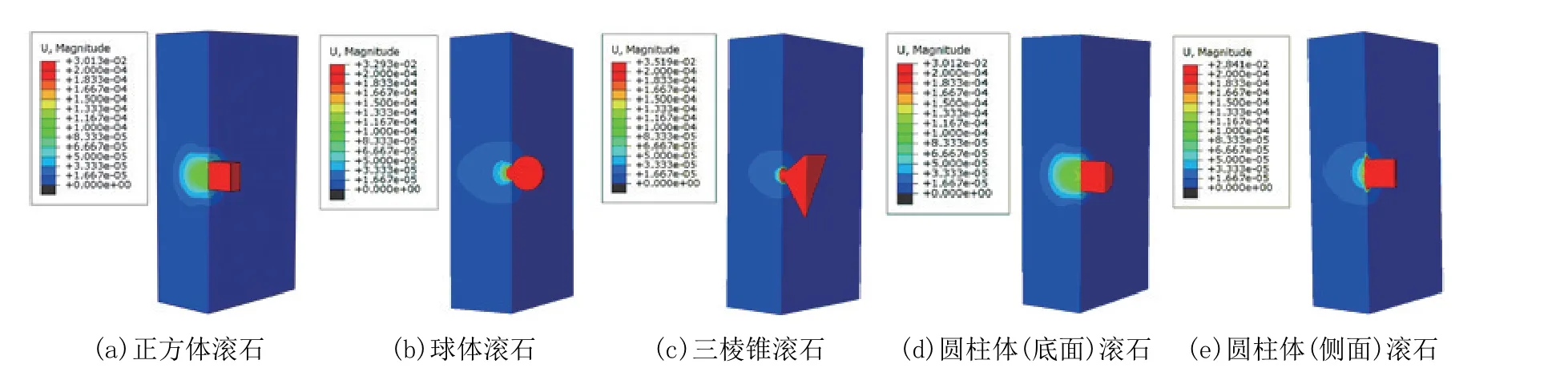
图9 不同形状滚石冲击结构物时的中心剖分模型位移云图Fig.9 Displacement contours of the central subdivision models when rockfalls with different shapes impact structures

3 滚石冲击不同表面形状结构物分析

建立的滚石冲击不同表面形状结构物的数值计算模型如图6（a）所示。为进一步探究滚石冲击过程中的动力响应特征，建立了如图4所示的4种不同表面形状的结构物，并将滚石形状均设为正方体。

3.1 滚石冲击力分析

图10为不同表面形状结构物工况下的滚石冲击力时程曲线，可以看出，4种结构物表面形状相对于平面时的冲击力峰值（1432.41 kN）都有所减小，冲击力峰值大小依次为凸面（914.13 kN）＞凹面（740.05 kN）＞波浪面（456.29 kN）＞斜面（262.46 kN），它们分别减少了36.18%、48.34%、68.15%和81.68%，其中，斜面状结构物的滚石冲击力时程曲线峰值出现了2次，这是由于正方体滚石在接触斜面时先是滚石的下部与之接触，使滚石发生偏转，继而滚石的上部再次与之碰撞，且2次的冲击力峰值相差不大。

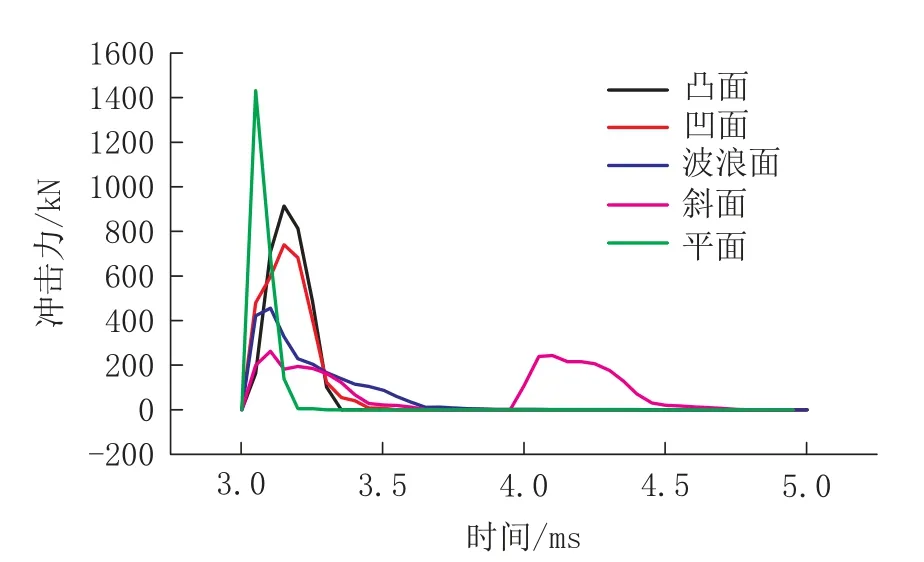
图10 不同表面形状结构物工况下的滚石冲击力时程曲线Fig.10 Time history curve of rockfall impact force on the str uctures with var ious shapes

3.2 结构物位移变形分析

图11为上述各工况下不同表面结构物中心受滚石冲击时单元位移变形量时程曲线。其中，波浪状表面的结构物在受滚石冲击时所达到的位移峰值（0.93 mm）最大；斜面和凹面状结构物在受滚石冲击时的位移峰值基本相当（分别为0.60、0.59 mm），对比表面形状为波浪状时，其位移峰值约降低了35.5%；凸面状结构物在受滚石冲击时的位移峰值为0.39 mm，其较波浪状表面结构物降低了58.1%，较斜面和凹面状结构物约降低了35%；平面状结构物受滚石冲击时的位移峰值最小（0.13 mm），较凸面状结构物降低了66.7%。上述情况表明，当滚石冲击不同表面结构物时，其受冲击区域破坏程度大小依次是波浪面＞斜面＞凹面＞凸面＞平面。

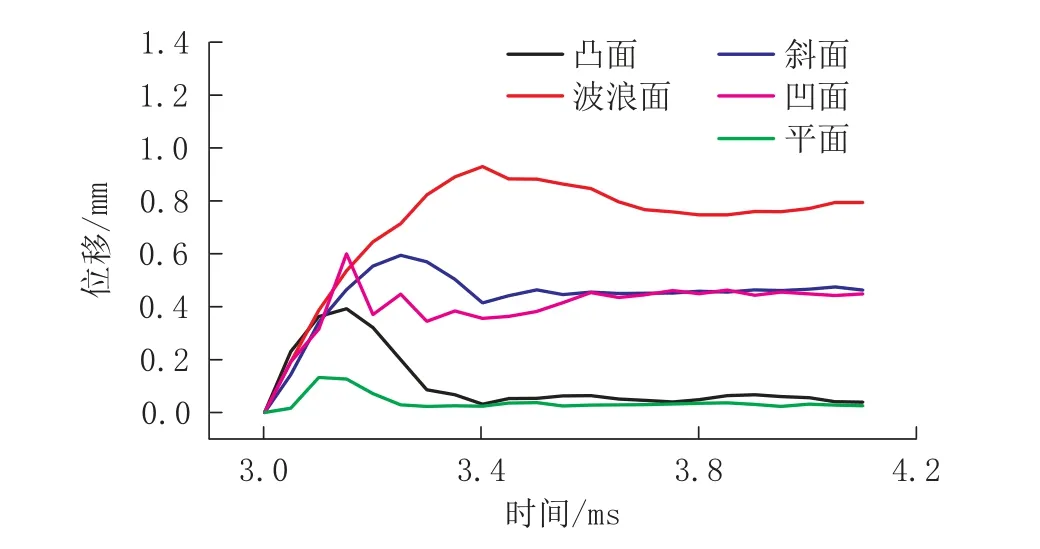
图11 不同表面结构物受滚石冲击时单元位移变形时程曲线Fig.11 Time history curve of the unit displacement of the structures with various shapes impacted by rockfalls

图12为正方体滚石冲击不同表面形状结构物时的中心剖分模型位移云图，可以看出：对于表面形状为凹面和凸面状的2种结构物，在承受滚石冲击时的整体变形区域较大，而对于表面形状为波浪面和斜面状的2种结构物，在承受滚石冲击时出现的整体变形区域小于前两者。

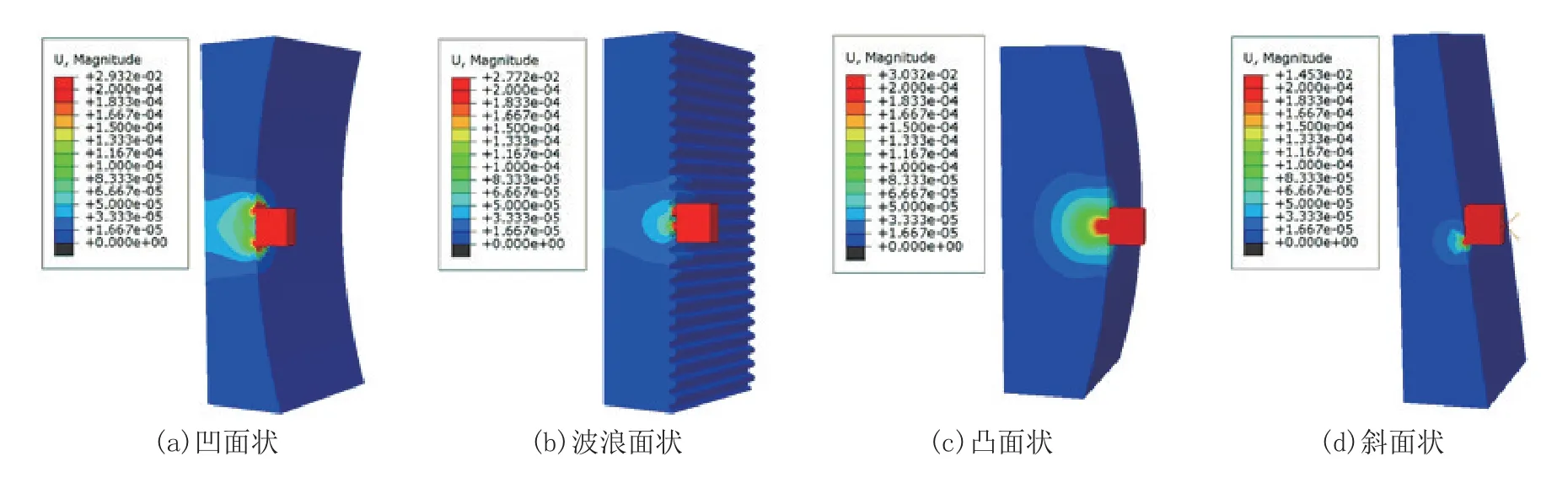
图12 正方体滚石冲击不同表面形状结构物时的中心剖分模型位移云图Fig.12 Displacement contours of the central division models when the cube rockfall impacts the structures with different surface shapes

综上所述，对于表面形状为凹面、凸面、波浪面和斜面状的结构物，斜面状的结构物具有更好的抵抗滚石冲击性能，虽然当其遭受滚石冲击后的位移变形量（约为0.47 mm）略大于平面状的结构物，但在上述4种表面形状的结构物中，斜面状具有冲击力小、结构简单、便于施工、节省材料及遭受滚石冲击时形成的整体变形区域很小等众多优点。

4 滚石冲击不同缓冲层分析

为减轻滚石冲击对结构物造成严重损害，现有研究多是在被保护结构（或滚石被动防护结构）前设置各种材质的缓冲层以降低滚石冲击力对结构物的损伤。将目前常用的EPS泡沫垫层、砂土垫层、泡沫铝垫层及EPS-砂土复合垫层4种缓冲材料的缓冲性能进行比较分析，对于EPS-砂土复合垫层，EPS置于结构物和砂土之间。采用的数值计算模型如图6（b）所示。

4.1 滚石冲击力分析

图13为不同缓冲层下的滚石冲击力时程曲线，从中可以看出，在缓冲层的耗能作用下滚石的冲击力被大幅削减。将各缓冲层作用下结构物所受最大冲击力大小排序依次为泡沫铝缓冲层（129.96 kN）＞砂土缓冲层（110.76 k N）＞EPS-砂土复合缓冲层（45.24 kN）＞EPS缓冲层（19.86 kN）。

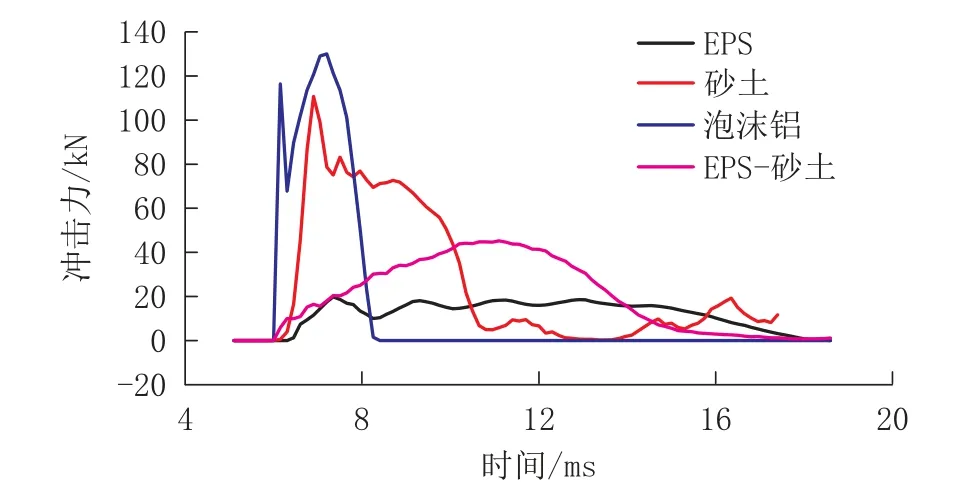
图13 不同缓冲层下的滚石冲击力时程曲线Fig.13 Time history curve of rockfall impact force for various buffer layers

因此，泡沫铝和砂土缓冲层对滚石冲击力的缓冲效果比另外2种缓冲层差，EPS和EPS-砂土复合缓冲层的缓冲效果较优。

4.2 缓冲层的缓冲性能分析

图14为设置不同缓冲层后滚石冲击结构物时的中心剖分模型位移云图，从图中可以看出，当在结构物前分别设置泡沫铝和砂土缓冲层后，结构物受滚石冲击处的位移变形量略大于在结构物前设置EPS-砂土复合缓冲层和EPS缓冲层时的工况。对比在结构物前无缓冲层，以及在结构物前设置EPS-砂土复合缓冲层和EPS缓冲层时的3种工况，可知结构物受滚石冲击区域的位移变形量减小显著。结合前述各缓冲层对滚石冲击力的缓冲耗能效果进行对比分析，可知EPS-砂土复合缓冲层和EPS缓冲层均为较优良的缓冲层型式，但EPS缓冲层在实际工程应用中尚有不足，当滚石冲击能级较大时，其极易发生破碎且不便清理，会对环境造成一定的污染，且其被破坏后需要及时更换，导致工程综合成本增加，耗费人力、物力，而EPS-砂土缓冲层在受滚石冲击时，由砂土率先消耗掉大部分的滚石冲击能量，再由EPS垫层承受由砂土缓冲后剩余的滚石冲击能量，由于砂土垫层的设置可大幅消减滚石对EPS缓冲垫层的直接冲切破坏，因而在实际工程中EPS-砂土缓冲层为一种更有广阔应用前景的缓冲垫层型式。

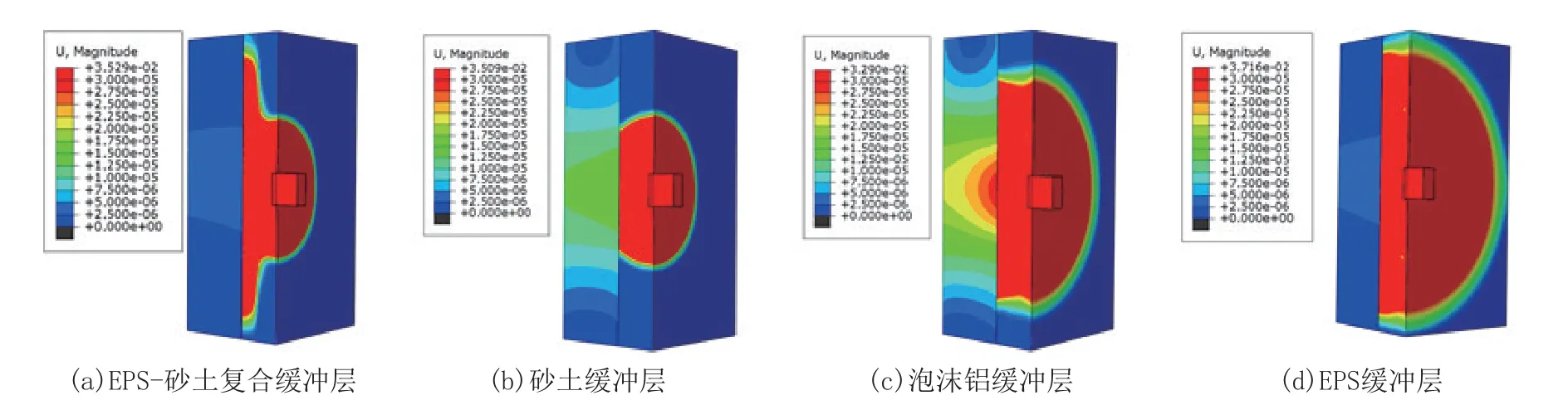
图14 设置不同缓冲层后滚石冲击结构物时的中心剖分模型位移云图Fig.14 Displacement contours of the central subdivision models when rockfalls impact structures with different buffer layers

5 结论

通过运用ABAQUS有限元软件中的Explicit动力有限元方法对滚石冲击结构物动力响应特征进行数值模拟研究，就本文研究假设的4种形状和几何尺寸的滚石建立的单一几何体模型而言，可得出以下主要结论：

（1）不同形状滚石对平面墙状结构物的冲击力峰值大小依次是正方体＞圆柱体（底面）＞圆柱体（侧面）＞球体＞三棱锥；滚石冲击面形状越尖锐，结构物受滚石冲击处的破坏程度越严重，但结构物内部整体变形区域越小；当滚石冲击面形状由“尖”变“钝”时，结构物受滚石冲击处的破坏程度变小，但整体变形区域变大。

（2）正方体滚石冲击不同表面形状结构物时，各形状结构物所受滚石冲击力峰值大小依次是平面＞凸面状＞凹面状＞波浪面状＞斜面状；其受冲击区域破坏程度大小依次是波浪面＞斜面＞凹面＞凸面＞平面；凹面状和凸面状结构物在受滚石冲击时的整体变形区域较大，而波浪面状和斜面状结构物形成的整体变形区域较小；相比而言，斜面状结构物具有较好的抗滚石冲击性能。

（3）对不同缓冲层的滚石冲击缓冲耗散性能进行对比分析，得出EPS-砂土复合缓冲层和EPS缓冲层的缓冲性能较优，但在工程实际应用中EPS缓冲层易被滚石冲切破坏，还会造成环境污染，因而EPS-砂土缓冲层为一种工程实际中更有广阔应用前景的缓冲垫层型式。

（4）本文提出的滚石模型均为规则样式，得到的相关结果和结论可为实际的滚石灾害防护提供一定的指导依据，但在实际的滚石地质灾害中，其形状较为复杂多样且不规则，使得其运动和冲击特性更为复杂，在后续研究中应进一步加强对非规则滚石冲击结构物动力响应特征的探究。