基于轨迹预测的双锚节点移动定位方法研究*

杨彩云，顾 锦，夏志东，毛科技，胡军国

(1.衢州学院电气与信息工程学院，浙江 衢州 324000；2.衢州市水利局，浙江 衢州 324000；

3.衢州市柯城区水利局，浙江 衢州 324000；4.浙江工业大学计算机科学与技术软件学院，浙江 杭州 310014；5.浙江农林大学信息工程学院，浙江 杭州 311300)

近年来在物联网(IoT)的许多应用场景中都需要实时和精确的位置信息，如在辅助导航、位置跟踪和其他基于位置的服务。全球卫星导航系统(GNSS)是目前存在的最普遍的RTLS技术。然而在室内环境(如商场、医院和工业仓库)中，由于墙壁和障碍物造成无线信号的非视距(NLOS)传播、多径和多通道干扰等现象，使得GNSS系统无法完成室内等相对复杂场景的目标定位。

目前常见的RTLS解决方案，通常使用射频识别(RFID)、Zigbee和超宽带进行测距定位。然而RFID存在信号传输距离短、Zigbee存在信号多径效应等不足，导致测距结果误差较大。为获得高精度的定位系统，使用超宽带(UWB)测距是较好的选择[1－2]。由于其带宽大，可以减少由墙壁和障碍物引起的误差源影响。大量的室内定位研究都是基于UWB技术开展，如参考文献[3]提出了一种新的3D到达时间(TOA)定位算法，该算法的主要思想是用新变量代替定位估计中的二次项，并使用加权最小二乘线性估计，然后与卡尔曼滤波器组合以减少传输过程中的干扰误差。参考文献[4]研究了天线方向对超宽带(UWB)实时定位系统的定位性能的影响，该研究的目的是评估当标签的天线方向未置于最佳方向时的对定位的影响。实验结果表明，当发射器和接收器的垂直天线方向与设备制造商推荐的参数差别较大，则对定位有显著影响。参考文献[5]为提高定位精度，利用多个冗余锚节点提高信号稳定性，并根据标签的绝对位置和移动信息来降低定位误差。参考文献[6]针对UWB连续定位跟踪问题，提出一种分区室内定位方法，克服一段时间内连续位置跟踪的限制，并将该系统应用于医院分析工作人员的工作量。文献[7]对UWB室内定位技术中基于TDOA的最小二乘(LS)方法，Chan算法和Taylor算法进行了分析，并在室内视线环境下利用动态和静态数据进行了测试。结果表明三种定位算法均可达到分米级定位精度。

虽然上述研究利用UWB技术可以实现高精度的室内定位，但都至少采用三个及以上的锚节点才可工作，如图1所示的三角定位法。我们知道目前UWB硬件的价格并不便宜，倘若定位场景较大，则整个室内定位系统的成本将非常高。而且锚节点数量越多，定位过程中消耗的能量越高，对定位系统长期生存是不利的。为提高室内定位性能，提出了一种基于轨迹预测的双锚节点移动定位方法。论文组织结构如下:第一章节介绍了定位过程中使用到的相关知识；第二章介绍了在二维平面和三维空间中的定位过程；第三章节介绍了基于LSTM模型的轨迹预测方法确定标签的真实位置；第四章对提出的定位方法进行实验分析；最后总结提出的方法。

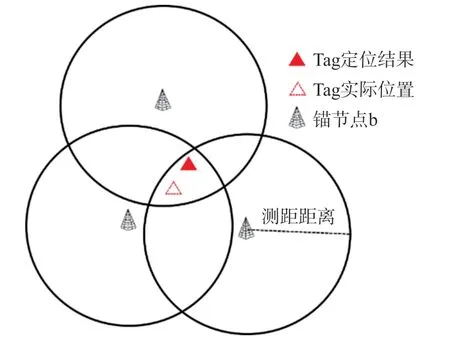
图1 三边定位

1 相关概述

1.1 UWB及测距原理

根据美国联邦通讯委员会(FCC)的定义，UWB是一种绝对带宽大于500 MHz，频率大于2.5 GHz的传输方式；或者对于频率小于2.5 GHz的系统，信号带宽与中心频率之比大于0.2。如图2所示，由于它们的带宽很大，超高的带宽可以屏蔽信号在传播过程中的多径和衰减效应，理论上可以减少由墙和障碍物引起的测距影响，因此能够准确的测量两节点间的直线距离。

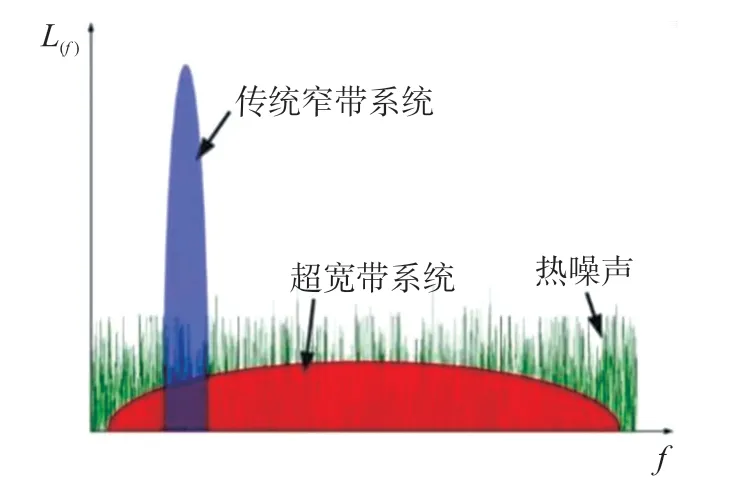
图2 超宽带图

使用无线测距实现室内定位有多种方法，但总体上可分为两类:①基于信号强度(RSSI)衰减测距的定位原理；②基于信号到达时间或到达时间差的测距，根据信号传输时间和电磁波在空气中传播速度计算两节点间距离。由于UWB技术的信号生存期很短，因此基于时间的方案比基于RSSI的方案能获得更精确的测距结果。在基于时间的方案中，利用飞行时间(TOF)测量标签和多个锚节点之间的距离。双向测距(TWR)涉及标签和每个锚节点之间的双向消息交换，测距机制如表1所示:

表1 TWR测距原理表

1.2 测距定位原理

利用节点间距离d或信号传播时间TOF，可以根据锚节点确定标签位置。主要方法可通过信号到达或信号到达时间差进行定位，分别如下所示。

①TOA定位算法

TOA[8－9]算法以锚节点为圆心，以标签与锚节点之间的估算距离d为半径，构建圆，三个及以上个锚节点形成的圆的交点即为标签的位置。二维空间标签位置的计算方法如式(1)所示。式中，di代表标签与锚节点i的估算距离，(xi，yi)为锚节点i的坐标，为已知值，(x，y)表示标签的坐标，为未知值，当锚节点的数量大于3时，即可计算出标签的坐标。

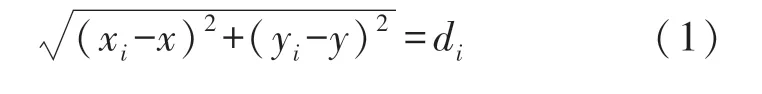
②TDOA定位算法

TDOA[10－11]代表到达时间差算法，与TOA相比TDOA的优点是不需要在锚节点与标签之间进行时间同步。由于锚节点和标签的时间不同步，需要计算TOF的偏移量，即到达时间差。通过TDOA计算形成的目标应该在双曲线的交点处。二维空间标签位置的计算方法如式(2)所示。

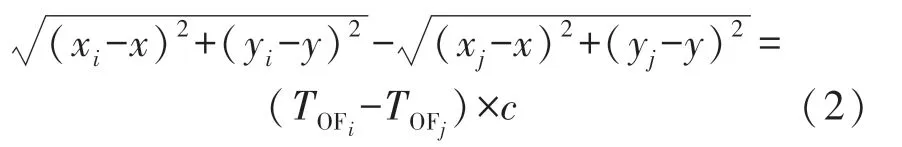
式中，(xi，yi)和(xj，yj)代表锚节点i和j的坐标，(x，y)表示标签的坐标点，TOFi和TOFj分别代表标签发出的广播信号分别到达锚节点i和j的时间。该方法同样在锚节点数量大于等于3时，才能解算出标签的坐标值。

2 定位原理

目前大量的WSN室内定位方法都基于二维平面进行讨论，而实际场景为三维空间，因此讨论三维空间的定位是非常必要的。本章节分开讨论以双锚节点进行二维平面和三维空间的定位问题，可采用TOA或TDOA进行定位。

2.1 二维平面预定位

首先将定位系统进行分割，每两个锚节点划分到一个区域中，如图3所示。当标签在某个区域中，则利用该区域的两个锚节点的已知信息(包括锚节点的坐标(xi，yi)和(xj，yj)、锚节点与标签之间的距离di和dj)计算标签的位置(x，y)。

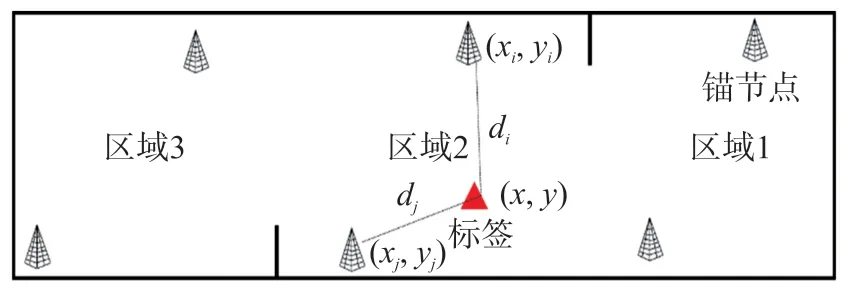
图3 二维平面定位原理图

利用式(1)构建二元二次方程对，如式(3)所示，即可求得标签的坐标(x，y)。但该方程可得到两个解，分别对应两个圆的交点T(x，y)和T′(x，－y)，如图4所示，这两个位置其中某一个为标签的实际位置T，而另一个位置为虚假位置T′，只要通过一定的方法排除虚假位置即可实现双锚节点的定位。

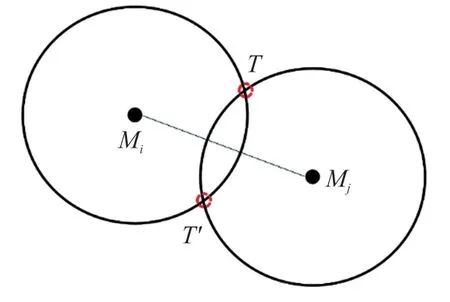
图4 坐标系转换图

2.2 三维空间预定位

在三维空间中同样将定位空间进行划分，每两个锚节点划分到一个长方体内，每个长方体称为一个小区，每个小区都包含两个锚节点。三维空间中锚节点Mi和Mj的三维坐标分别为(xi，yi，zi)、(xj，yj，zj)，锚节点Mi和Mj到标签T的距离分别为di、dj。利用上述已知信息可根据方程组(4)计算标签T可能的位置(x，y，z)。

式(4)是一个三元二次方程，存在三个未知数x、y、z，几何意义表示两个球面的相交位置，如图5所示。因此利用两个锚节点求得的标签位置为一个圆圈，标签的实际位置为该相交圆的某一点，但本文介绍到这里仅仅能确定标签位于该圆圈上，而无法具体确定具体哪个点是标签的位置。

图5 球面相交图

3 标签定位

一般现有的UWB定位方法需要三个或更多锚节点，这将消耗大量能量和成本。且目前的研究主要集中在静态对象上，而实际室内环境中更大的需求是对移动目标的定位，如商场内的行人等，因此本文以运动物体为定位对象。第2章节介绍了在二维平面和三维空间中，基于双锚节点的定位情况，但无论是二维平面还是三维空间，都能获得2个甚至多个定位结果，因此并不能真正意义上使用两个锚节点完成对标签的定位。本章节主要介绍如何利用标签的历史定位结果从当前多个预定位结果中选择一个最终且准确的位置作为标签的定位结果。

3.1 LSTM轨迹预测

移动标签在移动过程中会呈现趋势性和连续性，如人行走，不会出现很大跨越的情况，因此可以利用轨迹预测方法对下一个时间t即将到达的位置进行预测。标签的运动轨迹可用式(5)表示。

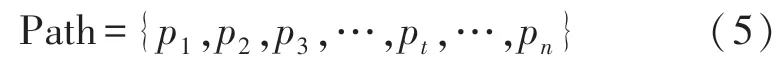
式中，1≤t≤n，n表示轨迹中定位点的数量，pt表示t时刻标签的坐标(xt，yt)或(xt，yt，zt)。

假设标签在定位区域中以匀速v移动，由于标签移动在时间上具有趋势性和连续性，因此本文采用时间关联性较强的深度学习模型LSTM[12－14]对轨迹进行预测，具体预测过程如下所示:

在深度学习中循环神经网络(RNN)能够较好的处理时间序列上的问题，RNN的输出由当前的特征输入和前一时刻的状态决定，如图6所示。将标签轨迹序列Path输入到RNN模型中，则该模型隐藏层的输出ht如式(6)所示。

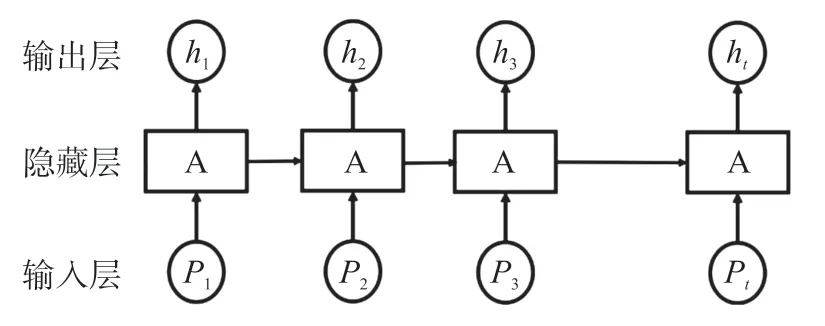
图6 RNN结构图

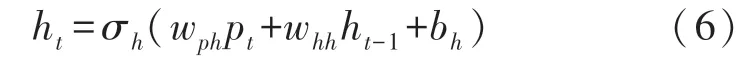
式中，σh表示输出的激活函数，wph、whh表示网络内部相邻层之间的权重矩阵，ht－1为模型上一时刻的状态，bh表示偏置系数。

RNN的输入层输出结果如式(7)所示。

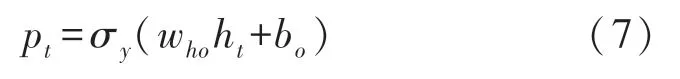
式中，σy表示激活函数，who表示输出层与隐藏层之间的权重矩阵，ht表示隐藏层的输出结果，bo表示输出层偏置系数，pt表示标签位置预测结果。

由于RNN模型随着时间序列的加长，模型变深以后会存在梯度消失的情况，为解决该问题，引入LSTM模型，该模型是一种RNN的变种，能够长期存储记忆。其基本单元相同，如图7所示，将该基本单元替换RNN模型中的结构A即为LSTM模型。该模型的基本单元包含输入门it，遗忘门ft和输出门ot，其中输入门和输出门用于控制信息流的输入和输出，遗忘门用于控制前一时刻的状态，该结构通过这三种门实现长期的记忆，LSTM结构中的参数如式(8)所示。

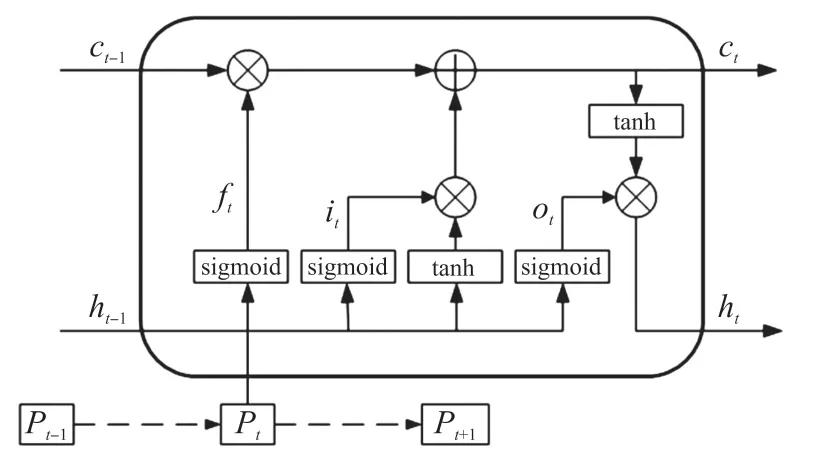
图7 LSTM单元结构图

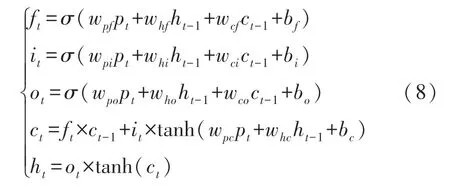
式中，wpf、whf、wcf、wpi、whi、wci、wpo、who、wco、wpc、whc都表示模型内部的权重值；bf、bi、bo、bc都表示模型的偏置参数；ct表示在t时刻模型的输出状态，ht表示t时刻隐藏层输出结果，将ht输入式(7)即可得到t时刻标签T的预测位置。

3.2 位置确定

利用LSTM模型预测标签轨迹是一种较可靠的方法，但本文并不需要预测标签未来可能到达的几个点，仅需要预测标签下一个时刻的位置(如图8所示，p1－p5表示已知的轨迹，根据历史轨迹预测出下一时刻标签可能到达的位置p′6)，然后结合第1～2章节的内容即可实现双锚节点的定位。

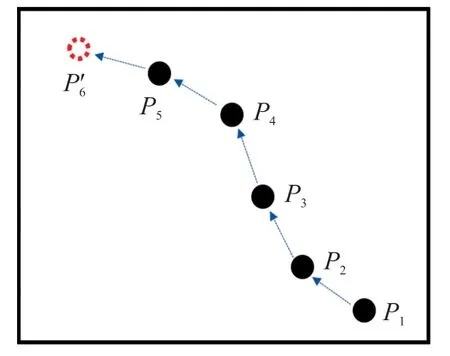
图8 标签轨迹预测图

将标签轨迹中上一个已知点和当前的预测结果以直线连接，如图9中p5表示上一时刻的定位结果，p′6表示利用LSTM模型预测的下一时刻的位置。将两个位置直线连接，在二维平面上利用两个锚节点进行定位，计算得到两个位置都可能是标签的实际位置(见图4)，如图9(a)中T和T′所示，其中位置T与直线的垂直距离为D1，位置T′与直线的垂直距离为D2，且D1＜D2。由于标签在移动过程中具有一定连续性，因此位置T是标签实际位置的概率高于位置T′，因此可以确定t时刻，对标签的定位结果为T位置。

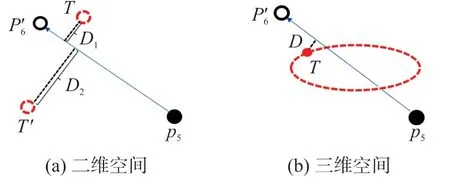
图9 定位结果确定原理图

在三维空间中，标签的预定位结果为一个圆(如图5)，而标签的实际位置位于圆上的某一个点，与二维平面确定标签位置相同，将圆上某个距离直线最近的一个点作为标签的定位结果，如图9(b)所示。双锚节点定位算法的具体流程如表2所示。

表2 双锚节点定位流程表

4 实验分析

实验采用MATLAB平台和真实室内场景进行测试分析，基于TOA算法进行定位。采用平均定位误差AE作为衡量定位精度的标准，如式(9)所示。

式中，(x，y，z)表示标签的实际坐标，(xi，yi，zi)表示定位算法计算得到的标签坐标，n表示定位的点数。

实验中以仿真方式模拟标签在定位区域中移动，每条路径由200个点组成，且标签移动具有连续性。利用模拟方法收集定位区域内3 000条移动轨迹，用于LSTM模型的训练，默认情况下传感器节点的最大通信半径R为30m。

4.1 二维平面定位实验分析

二维平面定位采用仿真方式进行，定位区域长为120m，宽为80m，实验中锚节点数量为15个，标签的数量为30个。为验证定位精度，标签的实际位置是已知的。实验结果如图10所示，为标签移动第5次之后的结果，即在该结果之前，移动标签已经完成了前4次定位。

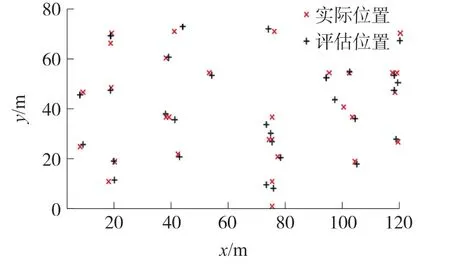
图10 二维平面定位结果图

实验结果表明本文提出的双锚节点定位算法对标签的定位结果是可靠的，标签的估算位置与实际位置之间的距离非常接近，有些标签的定位结果与实际结果甚至重叠了。

为验证定位算法对移动标签的定位性能，以图10中某个标签为实验对象，标签匀速在定位区域内移动，连续对标签进行定位，实验结果如图11所示。图11(a)表示标签的实际移动路径，图11(b)表示利用本文算法对标签连续定位的散点图，图11(c)表示将定位散点图按顺序连接后，再利用Kalman滤波算法进行滤波得到的标签轨迹。

图11 轨迹定位结果图

实验结果表明对移动标签的定位得到的轨迹与标签实际移动轨迹重合度非常高，该散点图的平均定位误差AE为6.43 cm。利用kalman滤波算法对轨迹散点图进行滤波处理后得到的轨迹图与标签实际轨迹重合度更高，平均定位误差为5.24 cm。

当定位区域中锚节点数量不同时，理论上对定位精度存在影响。本实验在定位区域内随机部署不同数量的锚节点，对30个标签进行定位，实验结果如表3所示。

表3 二维平面不同锚节点数量的定位误差

锚节点数量为5个时，平均定位误差为16.71 cm；锚节点数量为10个时，平均定位误差为11.36 cm；锚节点数量增加5个，其平均定位误差降低了5.35 cm。当锚节点数量为15个时，平均定位误差为6.48 cm；锚节点数量为20个时，平均定位误差为6.35 cm。从15个锚节点增加到20个时，定位误差仅仅降低了0.13 cm，基本没提高，因为本文仅采用2个锚节点即可实现定位，对锚节点数量没有太高要求，因此后续锚节点增加，对定位精度的提高帮助也不大。

4.2 三维空间定位分析

在三维空间中利用DWM1000模块(UWB模块)进行实物实验，部署两个UWB模块作为锚节点，一个UWB模块作为移动标签，如图12所示。两个锚节点距离地面的高度都为1.3 m，两个锚节点之间的距离为6.6 m，标签节点的高度z可调整三角架改变，实验过程中定位高度z如表4所示。移动标签从位置a移动到位置b，总共定位9次，实验结果如图13所示。

图12 三维定位场景图

表4 标签节点高度表

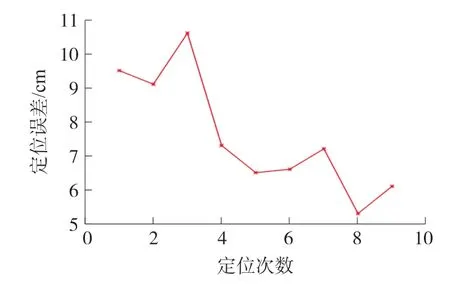
图13 三维定位误差图

在三维空间中进行定位，实验结果表明在对实物标签进行9次定位中，误差最大为10.6 cm，误差最小的定位点为5.3 cm，九个定位点的平均定位误差AE为7.58 cm。

4.3 传感器节点通信半径对平均定位精度影响分析

二维平面定位采用仿真方式进行，定位区域长为120 m，宽为80 m，实验中锚节点数量为15个，标签的数量为30个。在三维空间中的定位同上所述。分别在两种情况下，对传感器节点通信半径对平均定位精度的影响进行分析，传感器节点的通信半径取值范围从10 m到40 m，间隔5 m取值。实验结果如图14所示。

图14 传感器节点通信半径对平均定位精度影响图

实验结果表明，在二维定位以及三维定位中，平均误差AE的值随着传感器节点的最大通信半径的增大而降低。在达到30 m后，平均误差降幅不明显。与此同时，在增大传感器节点最大通信半径的同时，其开销也会增大。在达到30 m之后，增大传感器节点的最大通信半径的收益不高，最终决定将传感器节点的最大通信半径定位30 m。

4.4 对比分析

本文提出的方法利用两个锚节点即可实现定位，理论上可以在锚节点稀疏的情况下实现高精度的定位。本实验对比了参考文献[5]提出的基于冗余锚节点的定位优化方法和文献[15]提出的基于时间逆转的两步TOA估计算法进行对比。文献[5]提出的定位算法需要锚节点的数量多于3个，文献[15]提出的定位算法至少需要3个锚节点。实验在一个5 m×5 m的二维平面进行，定位50个标签的位置，通过改变定位区域中锚节点的部署数量验证三种算法的定位精度，实验结果如图15所示，横坐标为锚节点数量，纵坐标为平均定位误差。

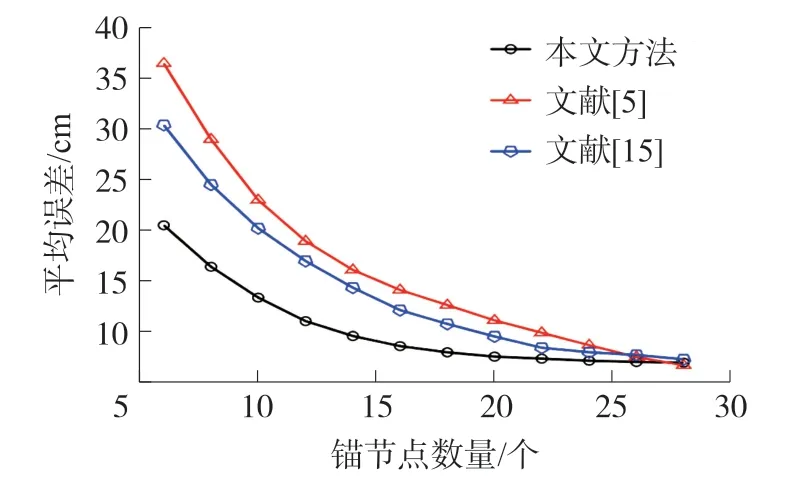
图15 定位精度对比图

实验结果表明随着定位区域内锚节点数量增加，三种方法的定位误差首先都快速降低，当锚节点数量达到一定值时，定位误差降低速度变缓。因为锚节点增加以后，定位过程所需要的锚节点数量区域饱和。在相同数量锚节点时，本文提出的方法定位误差最小，其次是文献[15]提出的两阶段TOA定位算法，最后是文献[5]提出的冗余锚节点定位算法，因为本文定位算法最少需要两个锚节点即可完成定位，对锚节点的需求小于文献[15]的方法，而文献[5]对锚节点的需求最大，该方法需要三个以上的锚节点来降低定位误差。

当锚节点数量不少于14个时，本文提出的定位方法取得的平均误差已经低于10 cm；文献[15]提出的方法当锚节点数量不少于20个时，平均定位误差低于10 cm；文献[5]提出的方法当锚节点数量不少于22个时，平均定位误差低于10 cm。综上所述，本文提出的方法能够在稀疏锚节点的情况下实现对标签的精确定位。

5 总结

针对目前大部分的室内定位算法需要至少三个锚节点才能实现定位问题，提出一种基于标签轨迹预测的双锚节点定位方法。利用标签的历史轨迹结合LSTM模型进行轨迹预测，然后从双锚节点定位结果中选择最佳位置作为最终的定位结果，并在二维平面和三维空间中讨论了定位效果，实验结果表明提出的方法能在稀疏锚节点的情况下实现高精度定位。