武警部队抢险救援任务

张亚楠 王浩鑫

摘要：武警部队肩负着维护国家安全、保障人民安居乐业等神圣使命。本文主要研究突发自然灾害时，救援物资的运送问题。

针对问题一，分别计算两个驻扎点途经补给站到两个受灾区的最短时间，再分配救援对象。计算最短时间时，采用0、1分配，以最短时间为目标函数，一个车队只救援一个受灾区为约束函数，建立优化模型，求解救援方案，最优救援路径见表3。

针对问题二，分别计算两个驻扎点途经补给站到10个受灾区的最短时间，再采用0、1分配，以最短时间为目标函数，一个车队只救援一个受灾区为约束函数，建立优化模型，得到最优救援路径见表6。

关键词：救援方案 0、1分配 优化模型

一、问题重述

某地区发生地震灾害，需要武警部队装载救援物资、迅速完成救援抢险任务，受灾地区的道路图如附件1，其中，红线是主干道路，为双车道，行驶速度为70公里/小时;蓝线为单车道，速度为45公里/小时，且机动车只能在道路节点会车。D1、D2两区域分别驻扎两个中队，Z01-Z02为6个物资补给区域，F01-F60为60个村庄。各物资补给区域每次只能容纳1个机动中队，每个中队物资装卸需要10分钟。

解决以下问题：

（1）若F02、F55为地震重灾区，设计从D1、D2出发到F02、F55的最优路径以顺利完成任务。

（2）若F02、F58、F14、F16、F41、F46、F49、F55、F57、F60为地震重灾区，从D1、D2向受灾区输送救援物资，D1、D2两区域的中队分别统一行动，然后返回驻扎点继续下一个输送任务。设计救援路径，使用时最少。

二、问题分析

针对问题一

我们假设车队出发时未装载物资，则需要先去物资补给区域进行补给，然后再去受灾区。由于不确定哪个中队救援哪个受灾区，所以我们先分别求出D1、D2经过6个补给站到F02、F55的最短时间，再进行比较得出救援组合方式。

求时间时，采用0、1分配，以最短时间为目标函数，一个车队只救援一个受灾区为约束函数，建立优化模型，求解救援方案，从而得出最短救援时间。

针对问题二

同样假设车队出发时未装载物资，则需要先去物资补给区域进行补给，然后再去受灾区，返回驻扎点再继续下一个救援任务。时间为车队往返驻扎地的时间，以时间最短为目标函数，一个车队只救援一个受灾区为约束函数，建立优化模型。

三、模型假设

1.假设车队在道路上行驶时没有其他时间损耗;

2.假设问题一、二车队出发时未装载物资。

四、符号说明

五、模型建立和求解

5.1问题一模型建立和求解

5.1.1数据处理

为了方便编写MATLAB程序，将附件中的要素编号按顺序重新编号为1，2，3……130，并且将题中所给图形中相连的线段的起点和终点依次找出，保存在附件2。结合每个节点的坐标，利用MATLAB里的graphshortestpath算法[1]，编写程序（见附录）将每条道路的路程求解出来，进而得到经过每条道路所花费的时间。

5.1.2模型建立

采用0、1分配，设第i个重灾区由j个驻扎地救援为1，否则为0则有：

设第一个重灾区是F16，第二个重灾区是F55，第一个驻扎地是D1，第二个驻扎地是D2。要求武警部队一个驻扎地出发后，先经过补给点补给物资，再运往重灾区，且一个驻扎地只救援一个重灾区，一个重灾区只被一个驻扎地救援，得到约束条件，。两个驻扎地的武警部队是同时行动，要求花费时间长的路线所用时间尽可能的少，则有，综上得到优化模型：

5.1.3模型求解

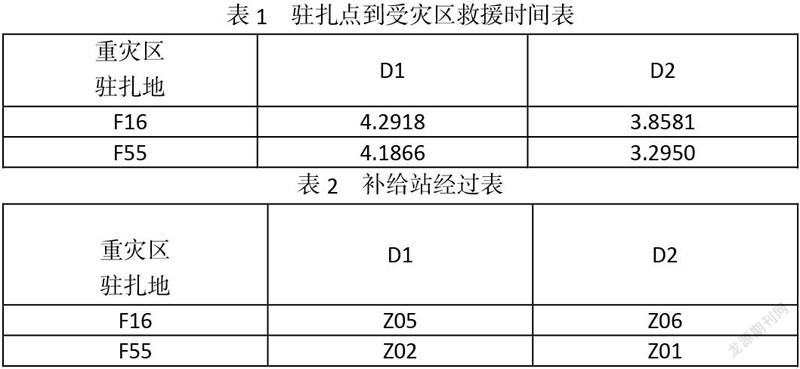
将计算得到的每条道路的时间矩阵，进行对角化和稀疏化处理，然后调用MATLAB图论工具箱中的graphshortestpath函数[1]，任意给定起点和终点，就可以得到两点所花费的时间和经过的节点。计算驻扎地到重灾区的时间时，中间可以经过的物资补给点一共有6个，依次计算经过每个补给点的总时间，保留时间最小的那一条路径，记录补给点的序号，编写MATLAB程序见附录程序一，得到时间表见表1，补给站经过表见表2：

本题数据较少，可以不用LINGO进行求解，观察即可得到D1的救援队在Z02进行补给之后前往F55，D2的救援队在Z06进行补给之后前往F16，具体路径如表3。

5.2问题二模型建立和求解

5.2.1模型建立：

采用0、1分配，设第i个重灾区由j个驻扎地救援为1，否则为0则有：

參考文献

[1].https：//blog.csdn.net/weixin_44228675/article/details/98070194

西安理工大学 710048