自动车床管理

张亚楠 王浩鑫

摘要：随着工业的快速发展，自动化生产应用越来越广泛。本文主要研究自动化车床管理中如何使工序设计效益最好问题。

首先我们通过对100次刀具故障记录的数据分析，得出概率密度和分布函数。

针对问题，我们以更换一次刀具为一个周期，计算该周期内每个零件的期望费用，每个零件的期望费用为总费用与零件总个数概率之比。其中总费用分为两种情况：（1）当到了定期更换刀具的时刻，即使设备未出现故障也进行刀具更换，（2）当检查出零件不合格时，调节并使其恢复正常。情况（1）的损失为所有次数的检查费用与更换刀具的费用，零件总个数为所有次检查的零件数;情况（2）的损失为发现故障进行调节使恢复正常的平均费用、所有次检查所需费用、故障后产出的零件损失费用三部分之和，零件总个数为所有次检查的零件数。每种情况对应的概率可由分布函数求出。由此我们建立以期望损失费用为目标函数的随机优化模型，求出效益最好的检查间隔为25，更换刀具间隔为376，每个零件的平均费用为6.6313。

一、问题重述

需要解决的问题

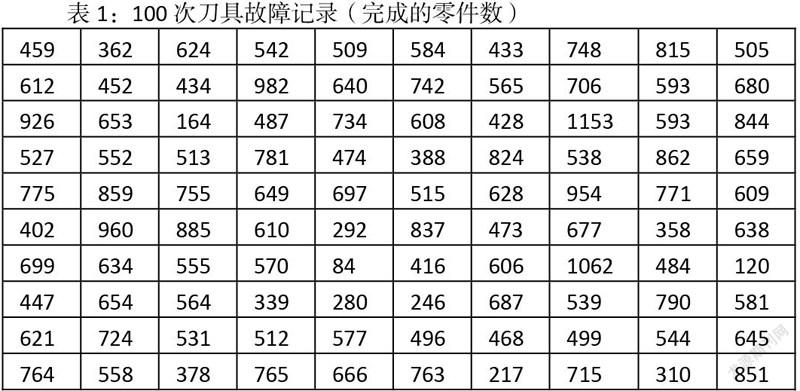
某自动化车床加工过程中会出现故障，其中刀具损坏故障占95%，其他故障仅占5%，工序出现故障随机且加工每个零件时出现故障的机会相等。且已知：①故障时产出的零件损失费用f=200元/件;②进行检查的费用t=20元/次;③发现故障进行调节使其恢复正常的平均费用d=4000元/次（包括刀具费）;④未发现故障时更换一把新刀具的费用k=1500元/次。100次刀具故障时该刀具完成的零件数如表1。

试解决：

假定工序故障时产出的零件均不合格，正常时产出的零件均合格，对该工序设计效益最好的检查间隔和刀具更换策略。

二、问题分析

要求设计效益最好的检查間隔和刀具更换策略，我们将相邻两次刀具更换作为一个生产周期，对零件进行检查，将一个周期内每个零件的平均费用作为目标函数，使目标函数最小。通过对100次刀具故障记录的数据分析，可以确定出刀具故障时完成的零件数服从正态分布。

要求在工序故障时产出的零件均不合格，正常时产出的零件均合格，设计效益最好的检查和刀具更换策略，我们给定检查间隔，对零件进行检查。计算平均费用分为两种情况：（1）当检查出零件不合格时，调节并使其恢复正常，（2）当到了定期更换刀具的时刻，即使设备未出现故障也进行刀具更换。计算两种情况下的计算得出加权总费用和零件总数量，并得出每个零件的平均损失，求平均损失最小情况下的检查间隔和刀具更换策略。

三、模型假设

1.假设发生刀具故障时，生产的零件数服从正态分布;

2.由于其他故障发生的概率很小，假设其他故障也服从正态分布;

3.刀具故障和其他故障的发生相互独立;

四、符号说明

五、模型建立和求解

5.1数据处理

利用MATLAB中的hist函数，画出100次刀具故障记录的频数直方图，如图1，观察图形可知，数据近似为正态分布。

（1）正态性检验[1]

正态分布的拒绝域为，取α=0.05，由于n=100，所以拒绝域为，。经计算可得：，未落入拒绝域中，故在α=0.05时，可认为刀具的故障记录满足正态分布。

（2）概率密度函数的求解

由数据可以计算得：μ=600，σ=196.63，则分布函数为。

5.2问题一的模型建立和求解

5.2.1模型建立

Ⅰ.计算总费用分为两种情况[2]：（1）当到了定期更换刀具的时刻，即使设备未出现故障也进行刀具更换，（2）当检查出零件不合格时，调节并使其恢复正常。

对于情况（1），损失为s次的检查费用与更换刀具的费用，即

零件数为

对于情况（2），我们假设故障出现在第n次和第（n+1）次检查之间，则第（n+1）次检查之后需要调节使恢复正常。所以损失为发现故障进行调节使恢复正常的平均费用、（n+1）次检查所需费用与故障后产出的零件损失费用之和，即（注：为方便求解，这里我们假设故障发生在第n次和第（n+1）检查最中间，即第n次故障发生后，产出的故障零件有件。）

Ⅱ.综合情况（1）（2），列出目标函数平均损失。其中情况（1）（2）的概率占比可由分布函数公式得出：

对于情况（1），概率为

对于情况（2），由于故障出现在第n次和第（n+1）次检查之间，而n可以取任意小于s的整数值，则概率为。

5.2.2模型求解

即效益最好的检查间隔为25，更换刀具间隔为376，每个零件的平均费用为6.6313

5.2.3模型的推广

我们的模型也可以理解为多元函数的极值问题，在自变量是整数的情况下，可以用本模型的求解方法（穷举法）。在涉及到概率论的问题中，也有一定的应用。

参考文献

[1].秦新强，郭文艳，徐小平等.数学建模[M].科学出版社，2015.183-190.

[2].https：//wenku.baidu.com/view/2e00d38271fe910ef12df86c.html

西安理工大学 710048