基于多层小波分解的日前太阳辐照度预测研究

林琳 李超 于立杰

关键词：日前预测;太阳辐照度;小波分解

近年来，由于化石燃料的短缺及其对环境的不利影响，全世界范围内对部署采用太阳能发电的兴趣与日俱增。2019年，太阳能光伏市场比2018年增长25%，达到创纪录的50GW，使全球总量达到约300GW。2019年的年度光伏市场几乎是十年前全球太阳能光伏累计容量的近10倍，中国为全球太阳能的光伏增长做出了重要贡献，2019年光伏净新增容量和2019年底中国光伏总容量均居世界第一。然而，可再生能源发电的多样性阻碍了更多的太阳能渗透到电网中，随着光伏并网发电量和装机容量的增加，弃光弃电问题开始成为我国太阳能光伏产业面临的严峻挑战。

光伏发电功率输出的不确定性和波动性可以通过几种方式来解决，包括增加需求侧的参与、加强区域间的协调及平衡分配、增加储能设备及容量等。考虑到经济性和可行性等因素，光伏发电功率预测仍然是解决光伏发电系统不确定性和波动性问题最有效且最经济的方法之一。当前短期光伏发电功率预测可提供未来24小时的光伏发电量，这对于发电计划和系统调度是重要的参考信息。准确的进行光伏预测不仅能够帮助系统运营商和规划人员更好的管理光伏发电的可变性和不确定性，而且还可以使光伏发电厂受益，这是因为减少了由于预测发电量和实际产量偏差过大而产生的附加费用。

太阳辐照度是影响光伏电站发电量的主要因素，准确进行太阳辐照度预测对于光伏发电的逐级预测具有重要意义。受光伏电站微气象环境的影响，太阳辐照度数据既有稳定的、周期的部分，也有波动的、随机的部分。前者随时间变化，在晴天变化较明显，而后者主要受云团或阵雨等气象因素的影响，这两部分的比例也随不同的天气条件而变化。在多云或阴雨天时，原始数据的波动性增大，同时二者间的耦合将导致对数据序列波动模式的识别以及预测变得十分困难。

基于以上分析，小波理论以其在信号分析中的高效性而被许多学者应用到数据处理中，利用离散小波变换（DWT）将原始数据序列分解为近似分量和细节分量两部分。近似分量包含原始数据中的低频信息，而细节分量包含原始数据中的高频信息，这一过程被称为小波分解（WT）。由小波分解得到的两个分量还可以进一步分解来获取低频和高频分子序列。因此，通常被认为是高频噪声的数据序列的波动部分和随机部分可以利用小波分解进行提取和过滤。基于上述理论，将原始数据分解为一个稳定的子序列和许多高波动性的子序列，是提高在非固定天气条件下进行光伏功率预测的一种有效方法。与原始数据序列相比，这些分解后的子序列具有更好的规律性（例如更稳定的方差和更少的异常值），因此可以通过针对性的建模得到更为准确的预测结果。

为了提高太阳辐照度的预测精度，本文提出了一种基于多层小波分解的短期太阳辐照度预测方法。首先，对原始辐照度数据序列进行多层小波分解，得到多个子序列;其次，通过天气状态模式识别对原始数据序列和其子序列中的数据赋予天气模式标签;然后，针对各层小波分解的子序列建立多组人工神经网络模型预测未来辐照度;最后根据不同的天气类型选择相对应的多元预测融合模型将各组预测结果进行融合.得到最终预测结果。

1小波分解预测方法

小波理论以其在多尺度信息处理中的优势，为复杂数据序列分析提供了有效的工具。对给定母小波函数（t）及其对应的尺度函数（t），能够得到小波序列（t）和二进制尺度函數（f），如下所示：

根据Mallat所提的快速离散小波变换算法，可以通过多个低通滤波器和高通滤波器来获得特定层数小波分解下的近似分量和细节分量。

在预测研究中，原始数据序列中的多频分量一直是难点，由于不同成分的规律性通常有所不同，这些成分之间的耦合会增加模型输入和输出之间的复杂性，单一的预测模型不能很好地处理它们。小波变换可将一个原始数据序列分解成一系列表征数据趋势特征的近似分量和表征数据波动特征的细节分量。这些分解后得到的子分量序列能够更好地从不同维度表征原始数据的特性，通过针对性的预测建模可得到更为准确的预测结果。然后根据这些模型输出的结果，利用离散小波逆变换（IDWT）计算最终的预测结果。

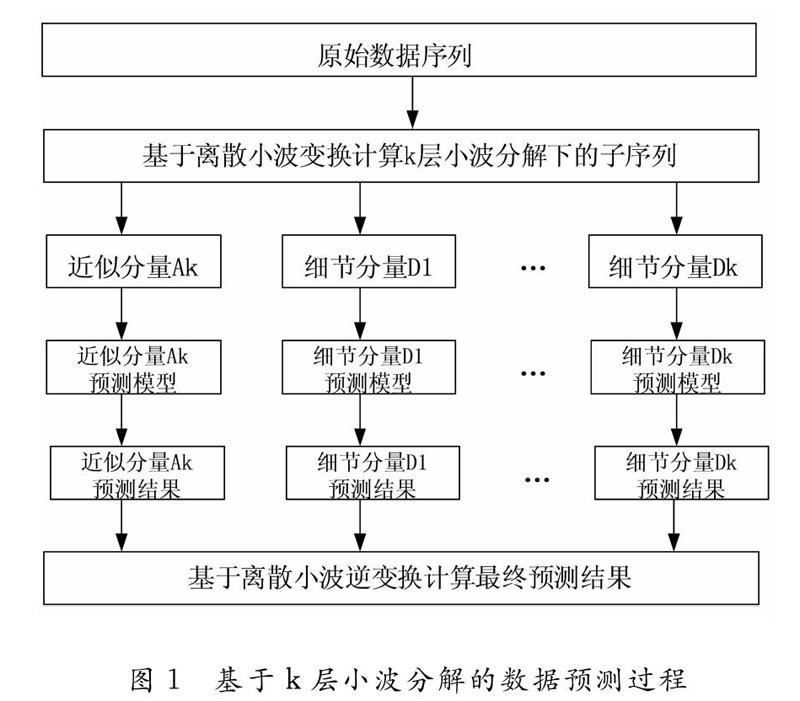
如果将小波分解的层数确定为k，那么经过小波分解后能得到原始序列S的子序列分别为第k阶的近似分量Ak，细节分量D1到Dk。小波分解的层数一旦确定为k，其子序列Ak与D1至Dk可以通过离散小波变换对原始序列数据进行计算得到。这样基于k层小波分解的数据预测过程如图1所示。

利用自回归（AR）模型、人工神经网络（ANN）和支持向量回归（SVR）等时间序列预测理论，可以分别对这些子序列进行预测。然后利用Ak和D1

Dk的预测结果进行离散小波逆变换计算对应原始数据序列的预测结果。

2太阳辐照度预测方法

根据中国气象局制定的国家标准，天气状况（即大气条件）分为33种天气类型。中，基于太阳辐照度特征提取和模式识别研究后，将33种天气类型划分为4个广义天气类型（GWC），分别命名为广义天气类型A、B、C和D。

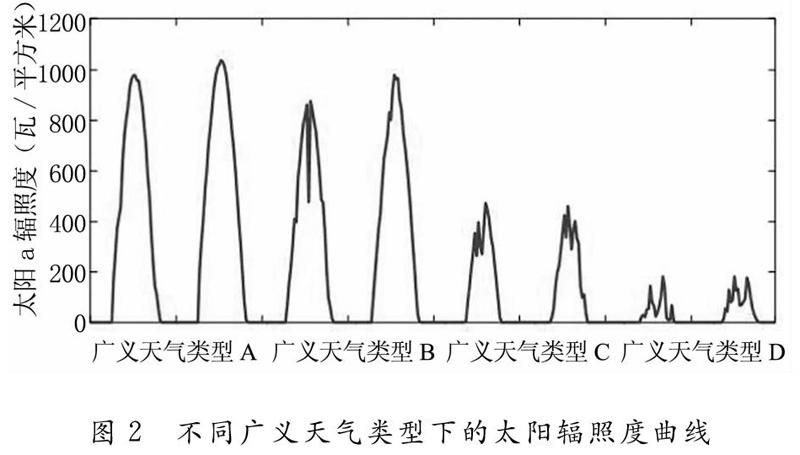
以内蒙古某光伏并网电站为例，测量了2019年1月1日至2019年12月31日的太阳辐射数据，时间间隔为30分钟，广义天气类型A，B，C，D。的辐射曲线如图2所示。

太阳辐照度的波动和变化特征与天气条件密切相关，在晴天等广义天气类型A中，太阳辐照度通常可以达到理论上的最大值，其辐照度曲线较为平滑。而在阴雨天（广义天气类型B或C），太阳辐照度值较低，辐照度曲线波动较大。因此，在不同的天气条件下进行预测建模是非常有必要的。

基于以上分析，提出了一种基于多层小波分解的太阳辐照度预测方法如图3所示。

首先，将所有的太阳辐照度数据按照广义天气类型进行分类，将具有相似特征的数据序列进行分组;其次，在每个广义天气类型下对太阳辐照度数据序列进行5层小波分解处理;然后，针对不同的小波分解层数和天气类型建立并训练多个人工神经网络。每一个预测日都能够得到6种预测结果，一种是基于原始数据预测所得，5种是分别基于1-5层小波分解数据预测所得。

为得到最终的预测结果，一个基于数据驱动的融合模型被应用，天气类型每天都会变，最优的小波分解层数也会改变，因此，固定的小波分解层数用于短期预测是不合适的，（仅采用固定的小波分解层数不能得到合适的结果）为了充分利用多层小波分解得到的数据子序列，建立了一个融合模型将6种预测结果融合为单一的预测结果。这个融合模型是通过支持向量回归实现的，其输入是特定时刻的6种预测结果，输出是该时刻的实际最终预测结果。

作为一种数据驱动模型，其性能在很大程度上依赖于训练样本，根据太阳辐照度特性差异，将所有训练样本分为与广义天气类型相对应的四个部分，并在不同广义天气类型下分别用历史数据对四个融合模型进行训练，已获得最佳的拟合效果。

根据从天气预测获得的预报日广义天气类型，选择同一广义天气类型下最近一天的辐照度数据作为输入，利用小波分解1-5层的原始序列和子序列进行辐照度数据预测，然后选择与预测日广义天气类型相对应的融合模型对6个输出结果进行融合，得到最终的短期太阳辐照度预测结果。

3仿真分析

运用MATLAB2015b进行仿真，我们分析了每个广义天气类型下的辐照度数据，其中60%的数据用于训练，40%的数据用于测试。为了评价预测精度，采用均方根误差（ RMSE）和绝对平均误差（MAE）两个误差指标来评价预测精度。太阳辐照度数据是在2019年1月1日至2019年12月31日在中国内蒙古的光伏并网电站中测量的，时间间隔为30分钟。201 9年有可用数据的共有310天。广义天气类型A，B，C和D的日子分别是第24、119、148和19天。

图4显示了用固定小波分解水平子序列训练的模型的精度和最终预测结果。

根据仿真结果，对于使用固定小波分解层数的预测模型，其模型的性能主要取决于选择的小波分解层数。通常，随着小波分解层级的变化，其预测精度会呈现先增大后减小的趋势，從广义天气类型A到广义天气类型D，天气条件越来越不稳定，而能够达到最佳精度的最优小波分解层数也随之提高。

然而，即使在同一特定的广义天气类型中，短期太阳辐照度序列的模式也存在不同程度的差异。因此，对于特定广义天气类型下的小波分解层数只是一个统计上的结果，并不一定适用于所有特定的天气模式，通过利用融合模型将不同小波分解层数的预测模型输出进行融合，进一步提高预测精度。

4结论

小波分解可以将原始数据序列分解成若干子序列，这些子序列分别表征原始数据序列的变化趋势，且具有较好的预测性能，可以有效提高预测精度。在这些基于小波分解的预测方法中，小波分解层数是影响预测精度的关键参数，而在短期太阳辐照度预测研究中，固定的小波分解层数并不适用于所有情况，这是因为在不同的天气条件下，辐照度子序列的特性会发生变化。

所有太阳辐照度历史数据均按照广义天气类型标签进行分组，然后对5层小波分解进行处理以获得辐照度子序列。首先利用不同小波分解层数下分解的子序列对次日24小时太阳辐照度进行预测，然后利用数据驱动融合模型将预测结果融合到最终的预测输出中。

仿真结果表明，短期太阳辐照度预测的最优小波分解水平与天气类型密切相关。对于辐照度波动较大的天气条件，使用高层小波分解获得的子序列通常可以取得更好的预测结果。而对于稳定的天气条件，使用低层小波分解获得的子序列将更适合。通过对基于小波分解的多层预测结果进行数据融合，进一步提高了最终预测结果的准确性，验证了本文方法的有效性。