多因素无人机倾斜摄影三维建模精度研究

王源，吕扬，李兵，陈品祥，韩雄

(1.北京市测绘设计研究院，北京 100038； 2.城市空间信息工程北京市重点实验室，北京 100038)

1 引 言

随着数字城市、智慧城市的快速推广[1]，无人机倾斜摄影测量以其高效率、高精度、高可视化进行实景三维建模的特点获得广泛关注[2，3]。实景三维建模已在规划设计、地质灾害治理、地籍调查、社区管理等领域中得到应用。已有应用研究表明，三维模型的精度对应用的成效具有一定影响作用，表1所示为模型精度在典型应用中所造成的影响。此外，在实际实景三维建模作业中，由于生产软件及硬件设施的条件限制，无法对大面积区域完成一次建模，一般需要进行分区建模，此时，建模精度将对分区接边的效果造成极大影响。为提高无人机倾斜摄影测量实景三维建模的效率效果及模型应用价值，有必要对影响建模精度的因素进行研究。

三维模型精度重要性 表1

由于航飞条件、外控布设条件、航线布设条件等多因素限制，在实际三维建模工作中，存在较难对某一因素进行控制的情况，无法通过控制单一因素达到控制精度的目的，因此，需要对多影响因素进行综合分析。在对精度的影响因素方面，现有研究主要单独针对控制点数量[13，14]、控制点分布[15]或航线规划[16]等单因素进行不同方案的对比分析，利用同一数据源进行多影响因素综合分析的研究比较匮乏。且在无人机倾斜摄影测量的成果类型方面，已有研究主要集中于正射影像和数字高程模型的精度研究[11，12]，直接对三维模型精度进行分析的研究较少。

本文针对影响模型精度的控制点数量、控制点分布以及航线布设三个因素设计不同方案，进行无人机倾斜摄影实景三维建模并完成精度验证，通过分析，为因条件限制造成的控制点布设困难提供方案参考，从多因素角度较为系统地为实际应用工作提出建议。

2 研究区与数据

研究选取北京市怀柔区某地区开展精度验证实验，研究区面积为 2.7 km2。研究区内包含平原区水泥厂区、山区采石区以及部分矮房居民区。平原厂区办公区海拔高度 96 m～102 m；山区采石区包含两座山，最高海拔高度 210.3 m；矮房居民区密集分布1层～2层建筑。所选研究区较为具有代表性，可涵盖一般工程区域类型。研究区如图1所示。

图1 研究区

本研究航摄数据获取使用成都纵横大鹏无人机科技有限公司CW-10小型全电动垂直起降固定翼无人机系统，搭载JR503五拼倾斜摄影相机(总像素1.2亿)。对研究区共进行3个架次航飞采集数据，每个架次均完全覆盖研究区。前期南北向飞行一个架次，后期为进行航线布设对精度影响实验，对研究区进行南北向和东西向各一个架次航飞(为防止时差问题对实验造成影响，南北向为重复飞行)，3个架次航向重叠度均为80%，旁像重叠度南北向为70%、东西向为50%。

控制点和检查点采用RTK技术外业测量得到。实验最终使用控制点和检查点坐标系均为北京地方坐标系。

3 建模精度研究方案

本文选取控制点数量、航线布设和控制点分布三个主要影响因素，设计对比实验，研究方案总体流程图如图2所示。

图2 方案流程图

3.1 控制点数量

为研究控制点(Ground Control Point，GCP)数量对建模精度的影响，分别选取5、8、12、15、20、26个控制点参与空中三角测量加密解算并完成三维建模。各组控制点选取均保证均匀分布，如图3所示。

图3 各组控制点分布图

3.2 航线布设

为探讨在控制点获取有难度、外业实测控制点少的情况下，增加交叉航线是否相较于单向航线对提高模型精度有贡献，设计三种航线布设方案(下述航线1、2、3)进行空中三角测量加密解算并完成三维建模。具体航线布设如图4所示，航线1：南北单向航线；航线2：在南北单向航线的基础上，增加东西航线形成交叉航线；航线3：在航线2的基础上，增加东西航线密度，形成高密度交叉航线。

图4 航线布设图

3.3 控制点分布

为研究控制点分布对建模精度分布的影响，以5个控制点为例，分别选取5种分布方式进行空中三角测量加密解算并完成三维建模。

图5 控制点和检查点分布图

五种控制点分布方案(下述5GCP_a、5GCP_b、5GCP_c、5GCP_d、5GCP_e、)间设计区别较大以使实验结果显著，控制点分布如图5所示，5GCP_a：四角加中心点均匀分布；5GCP_b：5个控制点集中分布在南部；5GCP_c：5个控制点集中分布在北部；5GCP_d：5个控制点集中分布在西部；5GCP_e：5个控制点分布在南北部且四角分布。

4 精度评价与讨论

选取14个外业测量点作为检查点进行精度评定，分布如图5检查点所示。检查点精度通过均方根误差来表示[15]，X方向(mx)、Y方向(my)、平面(ms)、高程(mh)的均方根误差通过式(1)、(2)、(3)、(4)计算得出。

(1)

(2)

(3)

(4)

为合理化实验方案，最大化利用实验数据，形成对比试验，使实验结果更为可靠，研究不同航线布设情况下控制点数量对模型精度的影响，以及不同控制点数量情况下航线布设对模型精度的影响，分别使用上述三种航线，将均匀分布的5、8、12、15、20、26个控制点引入空中三角测量解算，进而进行三维模型重建得到不同的18个整体三维模型，从每个模型中提取14个检查点的三维坐标作为模型匹配值，通过式(1)、(2)、(3)、(4)计算得出精度评定结果如表2所示。

检查点均方根误差 表2

根据《CH/T 9015-2012三维地理信息模型数据产品规范》如表3、表4对精度的要求，1∶500成图比例尺，非外业调绘情况下，平面精度为 0.5 m，高度精度为 0.8 m。根据表2，18个三维模型的平面精度和高程精度均可满足产品规范要求。

平面精度 表3

高度精度 表4

4.1 控制点数量

为便于分析不同数量控制点对模型精度的影响，将不同航线布设情况下，不同控制点数量的三维模型平面、高程均方根误差变化趋势以折线图形式呈现，如图6、图7、图8所示。

分析表2和图6、图7、图8可知：①三种航线均方根误差所呈现的整体趋势基本一致，即随着控制点数量增多，均方根误差减小，模型位置精度增高；②控制点数量的无限增多并不能使模型精度无限增高，三种航线均呈现出随控制点数量增多，均方根误差减少至极值的趋势，航线2和航线3的平面均方根误差以及航线1的高程均方根误差均出现小幅度增大的情况；③平面均方根误差整体高于高程均方根误差，这一特征不随控制点数量变化而变化。

图6 航线1平面、高程均方根误差折线图

图8 航线3平面、高程均方根误差折线图

4.2 航线布设

通过对比图9、图10中三种航线的折线图分析可得：①对于高程均方根误差，航线2误差最大，航线3次之，航线1的误差最小；②对于平面均方根误差，航线1误差最大，航线2次之，航线3误差最小；③交叉航线可一定程度提升模型平面误差，但会降低高程误差；④航线3较航线2在高程和平面上误差均低，即交叉密度大的在提升模型精度方面表现较好。

图9 不同航线平面均方根误差对比图

图10 不同航线高程均方根误差对比图

4.3 控制点分布

(5)

(6)

图11 5GCP_1检查点精度分布

图12 5GCP_2检查点精度分布图

图13 5GCP_3检查点精度分布

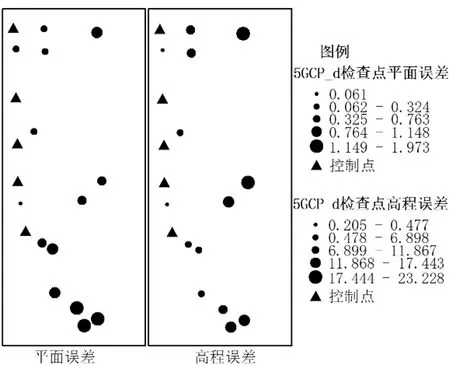
图14 5GCP_4检查点精度分布图

图15 5GCP_5检查点精度分布图

为研究控制点分布对mesh模型精度的影响，以5个控制点、航线1方案为例，进行不同控制点分布对模型精度影响的实验，均方根误差结果如表5所示，各检查点误差分布情况如图11～图15(图中各检查点误差均为绝对值，圆形由小到大代表差值绝对值由小到大)。根据表5，方案b、c、d的平面精度和高程精度均不满足产品规范，即控制点分布不满足四角布设的情况下精度无法达到产品规范对精度的要求。

根据表5和图11～图15可知：①相较于平面误差，控制点分布不均对高程误差的影响更大；②控制点分布不进行四角分布将造成误差超限；③从图中可以看出，控制点分布多的区域对精度的控制较好，控制点可控制区域有限；④方案e和方案a的均方根误差最大为 0.162 m，这两种方案均进行了四角分布；⑤5种分布方案中，方案一对精度的控制能力最佳，即四角加中心分布；⑥控制点布设有难度的情况下，必须保证四角布设，有条件时应至少保证四角加中心布设。

检查点均方根误差 表5

5 结 论

本文研究区内包含平原区水泥厂区、山区采石区以及部分矮房居民区，较具有代表性，可涵盖一般工程区域类型。研究表明，控制点数量、控制点分布及航线规划等因素对三维模型精度的影响较大，因此，本文选取上述三个因素综合设计不同方案，选取6组不同数量控制点、3种航线方案、5组控制点分布分别引入空中三角测量加密解算并完成三维建模，选取14个检查点对各组实景三维模型成果进行精度评定，基于本文条件下实验结果得到以下结论：

(1)控制点数量越多，模型精度越高；控制点数量持续增加，模型精度增高趋势趋于平缓；12个控制点时性价比较高，即平均 1 km2约4～5个点。

(2)相较于控制点数量，控制点分布对模型精度的影响性更高，即使不满足 1 km24～5个控制点，保证四角分布的情况下精度也可满足产品规范要求。

(3)在无法增加控制点布设以满足分布要求和数量要求的情况下，交叉航线可一定程度提升平面精度。

(4)控制点布设必须保证四角布设，否则将造成精度超限和分区模型难以接边的结果。

(5)控制点所能控制的区域有限，为保证不出现分区建模接边分层问题，分区边缘需均匀布设控制点。

综上所述，在本文实验方案下，满足产品规范精度要求且最经济的方案为单向航线、5个控制点且保证四角分布的方案，平面中误差最大为 0.162 m、高程中误差最大为 0.106 m。在实际工作中对控制点进行布设时，相比较考虑控制点的数量，应对控制点分布进行更多关注，分区边缘控制点均匀分布尤为重要，将影响整体拼接效果和效率；如果存在无法增加控制点布设的情况，可考虑交叉航线，能一定程度提高模型精度。

本文结论可从多角度因素较为系统地为实际应用工作提出指导和建议，由于选区实验区较小，今后的研究应将研究区扩展至大面积和地势起伏大的区域。另外，随着无人机倾斜摄影测量技术的发展，免像控摄影测量技术也日益成为关注的热点[17，18]。免像控技术一般需要利用实时动态RTK测量系统及动态后处理差分PPK测量系统等差分定位技术，获得高精度位置、姿态信息，在满足产品坐标系统要求的情况下，今后的研究应考虑免像控技术对三维建模精度的贡献。