室外机无遮挡凹槽尺寸优化与模型研究*
重庆大学 刘 猛
华东建筑设计研究院有限公司 重庆大学 张紫薇
0 引言
热泵型房间空调器作为住宅与部分商业建筑常用的空调设备,主要由室内机与室外机组成,当室外机作为冷凝器使用时,室外机风扇促使空气与室外盘管内制冷剂换热,而室外机盘管温度是空调系统性能的影响因素之一[1]。室外机置于建筑立面,为满足建筑的外观要求,多放置于增设的凹槽结构中[2]。若该放置形式不合理,则往往会限制室外机换热,导致出风不畅或者回流,室外机进风温度升高,从而影响空调正常运行。有研究表明,空调冷凝器的进口温度每升高1 ℃,空调系统的COP约降低3%,当进口温度超过45 ℃时,会严重影响空调的运行[3]。因此,合理的凹槽尺寸及室外机放置条件对空调经济运行有重要意义。
已有研究分析了多种室外机放置条件对其热环境或系统性能的影响,研究表明室外机安置形式、百叶间距、百叶角度、室外风场均会影响室外机的热环境[4-5]。金梧凤等人在室外环境温度为35 ℃、室内机设定温度为18 ℃的特定工况下,针对室外机与墙体距离、与百叶距离及百叶开度等影响因素进行了实验研究,指出当室外机放置于凹槽中且外设百叶时,室外机与墙体的距离应大于80 mm,出风口与百叶最佳距离为300 mm,百叶开度为30°[6]。赵安强探究了室外机离凹槽侧壁距离、离凹槽上壁距离、离凹槽后壁距离、离凹槽前壁距离及百叶旋转角度对室外机进风温度等的影响,指出影响室外机散热的显著因素为凹槽宽度和高度,百叶角度应为向下15°以下[7]。Choi等人通过数值模拟研究了室外风从正面吹、侧面吹和无室外风情况下室外机的进风温度和能效比等,结果表明当正面风速达到4 m/s或左侧风速达到8 m/s时,热空气会进入上层设备,严重影响上层室外机的散热[8]。
已有研究更多地侧重于采用数值模拟,对室外机凹槽的尺寸和百叶角度等进行研究,通常凹槽尺寸设置过大不符合实际,且未同时研究室外机在凹槽中的最优放置位置及凹槽的间距与室外机进风温度的关系等。因此,本文采用焓差室实验,分别探究无遮挡凹槽的壁面与室外机的各间距对室外机换热和系统能效比的影响,建立凹槽各间距与室外机进风温度的数学模型,从而得出优化的凹槽尺寸和对应的室外机放置条件,为建筑立面设计及空调安装提供指导。
1 实验原理与装置
1.1 实验方法
根据GB/T 7725—2004《房间空气调节器》[9],房间空调器的制冷量可采用空气焓值法测量。因此,本文实验在焓差室中进行,并采用室内机空气焓差法测得室内机进出风比焓及室内机风量等,计算得空调制冷量,测得系统输入功率,即可得系统能效比。
制冷量、制热量及能效比的计算式如下:
(1)
qk=q+PE
(2)
(3)
式(1)~(3)中q为制冷量,W;qmi为空调器室内测点的风量,m3/s;ha1为空调器室内侧回风(干空气)比焓,J/kg;ha2为空调器室内侧送风(干空气)比焓,J/kg;V′n为测点处湿空气比体积,m3/kg;Wn为测点处空气含湿量,kg/kg;qk为制热量,W;PE为压缩机输入功率,W;EER为制冷能效比。
1.2 实验内容
由于住宅用户通常使用的分体空调制冷量约为2.5~7.0 kW,而其中制冷量为5 kW与7 kW空调的室外机尺寸相近,考虑到实验的普适性及经济性,本实验对象选用制冷量约为5 kW的定速分体式空调机。实验装置包括30 mm厚聚乙烯泡沫板搭建的凹槽(见图1)、焓差室内装置、热电偶等。室外机尺寸为921 mm×398 mm×712 mm(长×宽×高),置于凹槽中的正视图和安装位置如图2、3所示,其后间距L1、前间距L2、左间距L3、右间距L4及上间距L5为本文研究影响因素,这5个间距既可以确定凹槽尺寸,也可以确定室外机放置位置。

图1 焓差实验室凹槽内室外机实物图

图2 凹槽内室外机正视图

图3 凹槽内室外机安装位置
为分析室外机热环境变化,需测得室外机进风温度、出风温度和凹槽壁面温度。如图3所示,a、b两处为室外机进风口,在a处采用5点法设置5个热电偶温度测点,在b处均匀设置2个热电偶温度测点;c处为室外机出风口,在圆形出风口上均匀布置4个热电偶温度测点。凹槽后、左右、上壁面温度测点布置如图4所示。
1.3 实验工况
采用单因素实验,分别探究上述5个间距对室外机换热及系统性能的影响。文献[7]调研结果显示,最不利情况下室外机甚至紧挨凹槽壁面,而大部分研究尚未考虑该不利情况[10-11]。因此,本文分别使凹槽各间距从50 mm开始递增至350 mm/450 mm,裸装及各间距为50 mm时为对比工况,具体实验设置见表1。为探究不同室外温湿度情况下,无遮挡凹槽尺寸对室外机换热的影响,选取3种不同的室外温湿度进行实验,其室外干/湿球温度分别为工况A 35 ℃/24 ℃、工况B 43 ℃/26 ℃、工况C 29 ℃/21 ℃,室内干/湿球温度为27 ℃/19 ℃。

表1 实验工况 mm
2 实验结果分析
2.1 各间距对室外机热环境的影响
图5显示了室外干/湿球温度为35 ℃/24 ℃工况下,凹槽各间距变化时其室外机进风温度的变化规律。由于在凹槽中换热受限,使得室外机进风温度会在室外干球温度基础上有一定的增幅,当前间距增大时,对应的室外机进风温度急剧升高;而其他间距增大时,室外机进风温度的升高幅度逐渐减小,其中左间距增幅减小最多,右间距与后间距增幅减小最少。图6显示了凹槽壁面温度、室外机进风温度与室外机出风温度的变化规律,图中直线为y=x。由图6可知,室外机左侧壁面温度与室外机出风温度最接近,而后侧与上侧壁面温度与进风温度接近,右侧壁面温度相对最低,这与实验所用室外机的出风口及进风口位置有关,可以判断室外机出风受阻回流主要发生在左侧,因此可以初步判断室外机凹槽应保证其左侧有足够的空间(即左间距足够大)。

图5 35 ℃/24 ℃工况下进风温度变化规律

图6 室外机热环境与出风温度变化规律
2.2 各间距对热回流率的影响
热回流现象指空冷散热器排出的热空气又重新返回空冷风机吸入口而导致空冷散热器入口空气温度升高的现象[12]。热回流率既可以采用体积(质量)流量比值定义,也可以采用温差比值定义。由于难以测得室外机进风口的热空气流量,因此采用便于测量的温差比值定义法[13]。其计算公式为
(4)
式中tw1为室外机进风温度,即冷却剂进口温度,℃;tw为环境空气温度,℃;tout为室外机出风温度,℃。
由热回流率的定义式可知,当不存在热回流现象时,热回流率应为0,而全部回流情况下,热回流率为1,即热回流率越大,说明热回流现象越严重。图7显示了3种不同室外温湿度工况下,热回流率随不同间距的变化规律。由图7可以看出:与进风温度的变化规律类似,其中后、左、右、上间距增大时,热回流率减小,说明热回流现象得到一定改善;左间距改变对热回流率影响最大,使得热回流率从0.75左右减小至0.13,其次为上间距;后、右间距的增大对热回流的改善程度较小,当后、右间距分别从50 mm增大至350、450 mm时,热回流率仅减小了0.08~0.13;与其他间距对热回流的影响不同的是,前间距增大时,热回流率急剧增大,高者达到0.95,说明前间距增大会使得更多的室外机出风口热空气难以排出凹槽,从而返回至进风口,形成严重的热回流现象。

图7 热回流率随不同间距的变化规律
2.3 各间距对系统性能的影响
图8~12分别显示了相对能效比EER/EER′随后、前、左、右、上间距的变化规律,其中EER′为对应室外温湿度工况下室外机裸装时的空调能效比,使用系统相对能效比衡量凹槽变化对系统性能的影响。由图8可知:随着后间距增大,系统相对能效比从0.6增大至0.7左右,当后间距增大至250 mm后能效比变化缓慢;而随着前间距增大(凹槽外无百叶遮挡),系统能效比反而减小,在最不利室外环境下(43 ℃/26 ℃),前间距增大至100 mm时则导致系统停机,这是由于前间距的增大不仅会导致进风阻力增大,也会使得室外机出风不畅,从而使得部分热空气更容易与外界空气混合重新进入室外机内与盘管换热,形成严重的回流现象。

图8 相对能效比随后间距的变化规律
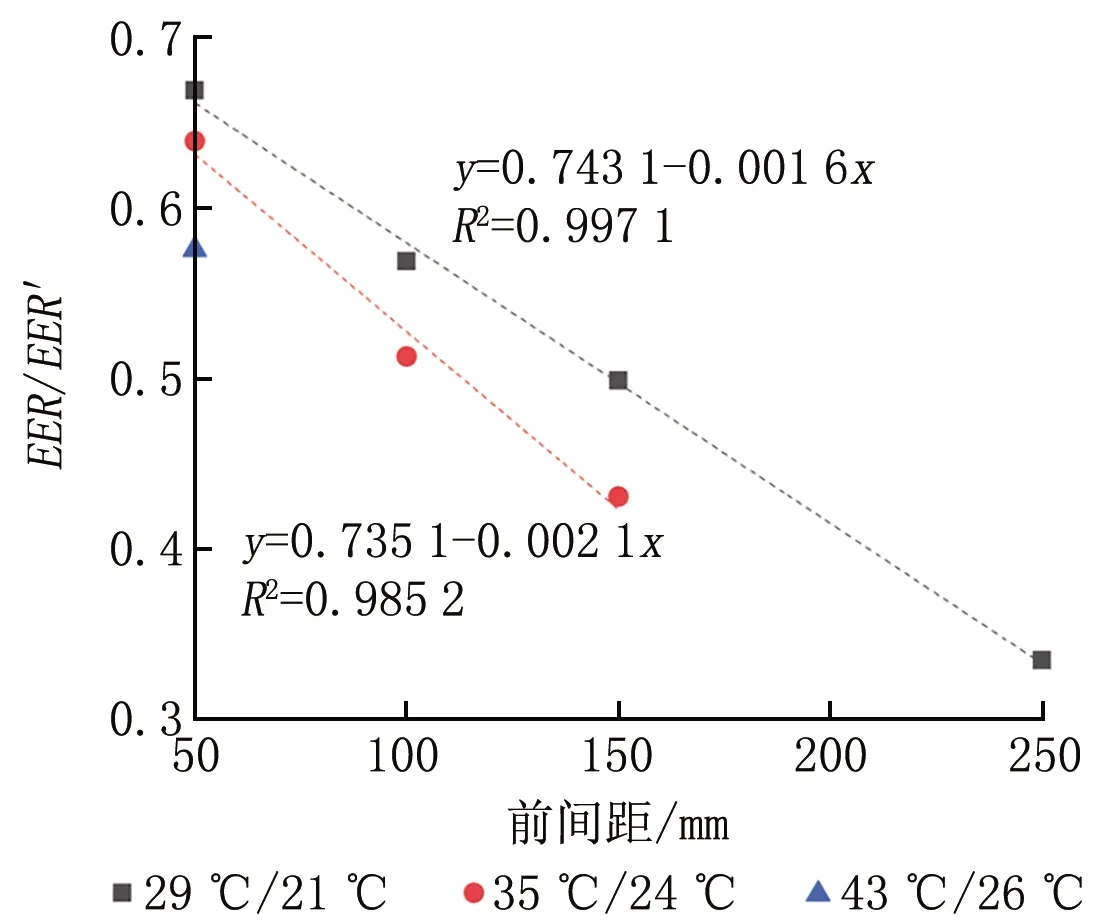
图9 相对能效比随前间距的变化规律

图10 相对能效比随左间距的变化规律

图11 相对能效比随右间距的变化规律

图12 相对能效比随上间距的变化规律
能效比受左间距变化影响明显,当左间距从50 mm增大至450 mm时,系统相对能效比EER/EER′从0.6左右增大至0.9左右,接近裸装效果,且在50~250 mm范围内变化明显。当右间距增至足够大(从50 mm增大至450 mm)时,其空调的相对能效比仅增加0.1左右,这是由于右侧靠近压缩机,而室外机出风位置偏左,且室外机进风位置在左侧与后侧,只有当右间距足够大时,才能使得部分外界空气从右侧进入室外机进风口。上间距在150 mm内变化时其能效比变化不大,而当上间距增大至250 mm后,相对能效比增大至0.87左右。因此,凹槽左、上、后间距增大时,对空调运行明显有利,且左、上间距影响较大;而前间距增大则不利于室外机运行。
3 模型建立
3.1 能效比与进风温度
对于特定的室内温度,房间空调器的EER可以使用下式进行计算[14]:
EER=a-btk
(5)
式中a、b为常数;tk为冷凝器盘管温度,℃。
实验中分析发现冷凝器盘管温度与室外机进风温度呈高度线性相关关系,因此直接探究进风温度与能效比的关系。图13显示了所有实验工况下能效比相对值EER/EER0(其中EER0为额定制冷能效比)及制冷量相对值q/q0(其中q0为额定制冷量)与进风温度的相关关系。结果表明,系统能效比相对值与室外机进风温度呈明显的线性负相关关系,即
(6)

图13 能效比相对值与制冷量相对值随进风温度的变化规律
制冷量与室外机进风温度呈明显的线性负相关关系,即
(7)
3.2 进风温度与凹槽各间距
由于室外机出风气流受到周边凹槽的阻挡,造成室外机出风回流,因此室外机通风量包括出风回流的热空气流量及环境空气流量,而其中环境空气流量为实际进行换热的风量。
冷凝器的换热量计算式为
qk=FRKCAC(tk-tw1)
(8)
其中系数FR的表达式为
(9)
式(8)、(9)中KC为冷凝器的传热系数,W/(m2·K);AC为冷凝器的传热面积,m2;M为(制冷剂)空气的质量流量,kg/s,应理解为实际换热部分;c为空气的比热容,J/(kg·K)。
本文认为KC、AC及c为常数,定义常数n=c/KCAC,因此,FR可简化为M的关系式:
(10)
由式(2)、(3)可得:
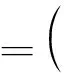
(11)
室外机实际换热风量直接受凹槽几何尺寸的影响,且室外机换热空气的密度变化不大,因此,假定M为L1~L5的多元线性函数值,即
(12)
由式(6)、(8)~(11)并结合tk与tw1的相关关系,经过多元线性回归可得:
(13)
式中L1~L5的单位为mm,其系数取值见表2。经过F检验及R2计算表明高度拟合,且通过系数可判断各间距对室外机进风温度的相对影响程度,对应上述分析:前间距增大,进风温度升高,则系统能效比减小;其他间距增大,进风温度降低,则系统能效比增大,且左间距与上间距的影响程度较大,其次为后间距,右间距影响程度最小。

表2 多元线性回归计算结果
4 优化分析
由图8~12可知,当后间距增大至250 mm、左间距增大至350 mm、上间距增大至250 mm时,系统能效比的增加变缓,而右间距增大对能效比影响不大,前间距增大对系统运行不利。因此,分别在3种室外环境下,测得实验优化后的凹槽各间距情况下的系统能效比。发现室外机在优化后的凹槽中时,其空调系统能效比与裸装时的值相差3%以内,因此,当室外机正确放置在优化的无遮挡凹槽中时换热效果接近于裸装。
由拟合关系式(6)可得出3种不同环境下室外机裸装时的进风温度,由此根据式(13)可得出,为达到裸装时的空调系统能效比,在同等效果下为保证凹槽尺寸最小(以体积衡量,即(L1+L2+0.398)×(L3+L4+0.921)×(L5+0.712)),其中L1~L5取值范围为50~350 mm,取值间隔为50 mm,最终通过L1~L5组合计算得出凹槽各间距的优化值,如表3所示。在3种室外环境下,凹槽后、右间距取值都为50 mm,这是由于两者增大对进风温度影响不大;前间距取值为50 mm,是由于该值增大对室外机出风不利;而左、上间距取值随着室外干/湿球温度升高而增加,且即使在29 ℃/21 ℃情况下,左侧仍需保证充足的空间,取值为250 mm。综合计算结果与实验所取最佳尺寸接近,因此当室外机放置在前侧无遮挡凹槽中时,应保证左侧与上侧空间充足,前侧空间尽量小,后侧与右侧空间保证安装空间即可。针对本文实验所用空调,其优化后的凹槽尺寸为698 mm×1 321 mm×1 062 mm(长×宽×高),各个间距为L1=250 mm,L2=50 mm,L3=350 mm,L4=50 mm,L5=350 mm。

表3 凹槽优化尺寸 mm
5 结论
1) 凹槽左间距对其进风温度与热回流率影响最明显,且室外机左侧壁面温度与室外机出风温度最接近,可以判断室外机出风受阻回流主要发生在左侧,这与实验所用室外机出风口偏左,左侧存在进风口有关。
2) 凹槽后、左、右、上间距增大时,空调系统能效比增大,而前间距增大时,空调系统能效比减小。且左、上间距影响较大:左间距增大400 mm时,其相对能效比增大至0.9左右,接近裸装效果;当上间距增大至250 mm后,相对能效比增大至0.87左右。其次为后间距和右间距,后间距增大300 mm时,其相对能效比增大约0.1,为0.7左右;而右间距增大400 mm后,其相对能效比增大不足0.1。
3) 系统能效比和制冷量分别与室外机进风温度呈明显的线性负相关关系,通过理论分析结合多元线性回归探究了室外机各间距与进风温度的关系,由此探究出的计算优化尺寸与实验优化尺寸接近,验证了上述关系式。
4) 当室外机放置在前侧无遮挡凹槽中时,应保证左侧与上侧空间充足(350 mm),前侧空间尽量小,后侧与右侧空间保证安装空间即可。优化后的凹槽尺寸为698 mm×1 321 mm×1 062 mm(长×宽×高),放置条件为L1=250 mm,L2=50 mm,L3=350 mm,L4=50 mm,L5=350 mm。当室外机安置于优化凹槽中时,其空调能效比可达到裸装时的97%。

