基于变边界分段模型的页岩损失气量和解吸气量评价方法1)

曾克成 解海鹏 姜培学 周尚文 胥蕊娜,2)

* (清华大学能源与动力工程系,热科学与动力工程教育部重点实验室,北京 100084)

† (中国石油勘探开发研究院,北京 100083)

引言

非常规天然气主要包括页岩气、致密气和煤层气,已有研究[1]通过对比中美两国天然气的发展特点,预测2035年我国非常规天然气年产量将升至1160 亿立方米,接近常规天然气产量,对我国能源安全和能源供应具有重要意义.虽然非常规天然气的勘探开发技术已取得长足发展[2],但是高效、准确和经济的储层含气量评估方法仍待突破,尤其是页岩气缺少储层含气量的准确评估方法.

评估非常规储层含气量的常用方法分为直接法和间接法.间接法主要包括等温吸附法等实验测量方法,等温吸附法测得储层的吸附气含量,并通过测井等方法得到游离气含量,加总后得到储层总含气量[3-4],但实验过程相对繁琐.直接法(也称解吸法)[5-6]将真实含气量分为损失气、解吸气和残余气三个部分,通过三部分加总获得储层含气量.图1(a)表示岩心在从井筒底部提升至地表的提钻过程中,会有部分气体逸散至井筒中且无法收集测量,这部分气体被称为损失气.由于损失气在总含气量中占比较高,例如部分储层的损失气占比达到40%～80%[7],因此对于损失气的估算一直是储层含气量测试和研究的重点.

岩心被提至地表后仍有气体从岩心里向环境中逸散,图1(b)表示将岩心装入解吸罐中密封,通过流量计等设备可测量气体逸散量与时间的关系,这部分气体被称为解吸气,解吸气流量与时间的关系被称为解吸曲线.当岩心内气体解吸速率小于流量测量设备的最小检测值后,可将岩心取样粉碎,加速气体逸散并测量逸散量,这部分气体被称为残余气.解吸气与残余气均可准确测量,但损失气难以收集测量,国内部分储层采用保压取心技术[8],在原始地层压力状态下减少岩心中油气组分的散失.但保压取心技术成本相对价高,所以现有方法大部分采用解吸曲线结合损失气估算模型来估算损失气量.因此,损失气估算模型的准确性和真实性直接决定了储层含气量评估结果是否可靠,其估算效率也直接决定了储层评估的经济性.

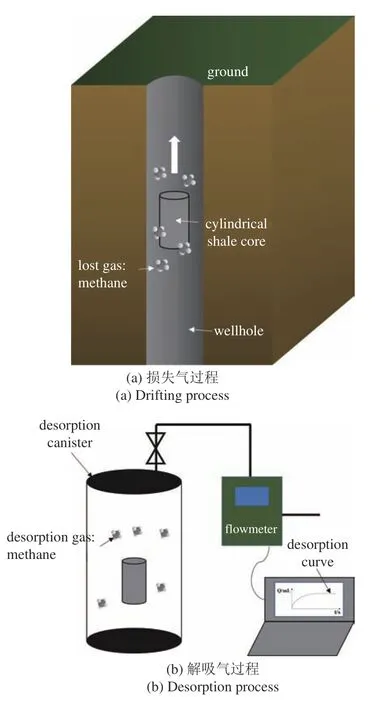
图1 非常规储层含气量直接法评估过程中损失气与解吸过程示意图Fig.1 Schematic diagram of the drifting process and desorption process in direct method to evaluate unconventional reservoir gas content

自1970年代起,国际上陆续开发了不同的非常规储层损失气估算模型,如USBM 模型、AMOCO模型和UniPore 模型等.其中,USBM 模型是美国矿业局的Kissell 等[9]在1973年针对煤层损失气提出的估算模型,该模型认为在解吸实验初期几个小时内,气体逸散量与逸散时间的平方根呈线性关系,并以此为依据将解吸曲线向前反推,达到提钻时间的一半,得到损失气体的逸散量

其中,Qt为时间t时岩心解吸气体的量,mL,Q∞为岩心解吸平衡后得到的解吸气总量,mL,与时间的平方根呈线性关系, β 为拟合常数,min−1/2,QL为反推估算的损失气量,mL,t0为提钻时间,min.

AMOCO 模型是在1993年由AMOCO 公司的Metcalfe 等[10]提出的,认为在提取煤样的过程中,气体逸散量随时间呈指数关系,通过解吸曲线可以拟合并反推得到损失气量

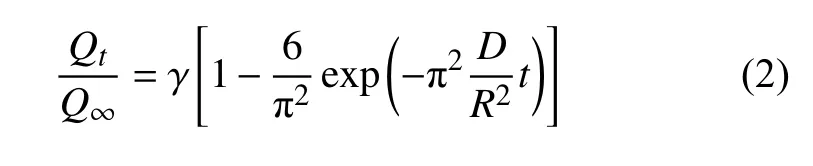
其中,D为扩散系数,m2/s,R为颗粒样品的特征半径,cm.

除应用较广的USBM 模型和AMOCO 模型之外,还有大量的其他模型,例如Airey 模型[11]、Smith and Williams 模型[12-14]等,Wang 等[15]列举了更多其他的模型.通过理论分析,可以知道这些模型均来源于UniPore 模型[16],UniPore 模型为估算煤层气的损失气而被建立的,该模型包括4 个假设条件:(1)煤样为球体;(2)边界条件为常压力边界条件;(3)不考虑温度变化对扩散系数的影响;(4)甲烷在煤样中初始分布均匀.求解后所得结果为无限求和级数形式

当时间t较小时,式(3)可以通过摄动展开,简化为

其中,ierfc()为高斯补误差函数的一次积分值.对比可知,式(4) 与式(1) 相同,说明USBM 模型由UniPore 模型简化得来,且USBM 模型仅在t较小的短时间内成立.

当截取式(3)中的第一项(即n=1)并加以修正之后,可以得到

对比可知式(5)与式(2),即AMOCO 模型相同,说明AMOCO 模型同样也是由UniPore 模型简化得来.

从上述分析可知,USBM 模型和AMOCO 模型均可由UniPore 模型简化得到,其余的针对USBM模型、AMOCO 模型进行修正得到的模型同样可由UniPore 模型推导得到[17],因此不作赘述.

以上的损失气估算模型在煤层气的损失气估算中发挥了重要作用,但在页岩气的损失气估算,尤其是我国深层储层的损失气估算中,出现了较大的误差和不确定性[18].由于煤层气埋藏较浅,取心速度较快,气体逸散较少,且煤岩有机质含量高,导致煤层气中吸附气占比大,气体散失速度慢,所以在取心过程中,煤层气的损失气占比远远小于页岩气中的损失气占比.由于损失气占比巨大,页岩气的损失气估算模型不能完全采用煤层气的估算模型,需要建立更加精确、更加符合工程实际的页岩损失气估算模型.

1 模型建立

1.1 控制方程及初边值条件

页岩岩心的钻取与煤样钻取存在着不同,由于页岩较为坚固,所以岩心保持圆柱状,控制方程应当采用柱坐标系.而煤样容易破碎,样品为颗粒堆积状,可以简化为球体,采用球坐标系.而且由于页岩气藏的埋藏较深,提钻过程逸散的损失气占比较大,相较于煤层气中的损失气模型,更应该考虑提钻过程与解吸过程之间的差别,分别开展研究.因此,页岩损失气与煤层损失气的不同主要体现在两个方面[19-20]:(1)页岩岩心呈圆柱状;(2)页岩的提钻时间长、压力降低范围广,变压力边界条件不可忽略.从而,建立变边界分段模型.

本文以长度为18 cm、直径为10 cm 的圆柱岩心为研究对象,如图2(a)所示.假设气体从岩心内向环境的逸散为扩散过程,并将岩心简化为无限长一维圆柱体,只考虑径向方向气体的扩散,忽略周向及轴向的三维作用,得到提钻和解吸过程中气体扩散的控制方程[21-23].图2(b)表示提钻和解吸过程中岩心的边界条件随时间变化,在提钻过程为线性降压的边界条件,在解吸过程为恒压边界条件.

图2 页岩柱状岩心和提钻过程及解吸过程的压力边界条件Fig.2 Shale cylindrical core and pressure boundary condition in drifting process and desorption process

基于以上假设,可得圆柱岩心的一维扩散方程

其中,C表示岩心中气体的浓度,r表示径向坐标,D表示气体在岩心中的表观扩散系数.

在提钻阶段,岩心内气体的初始浓度为均匀分布,随着岩心提至地表,环境的压力逐渐降低,岩心的浓度边界也随时间降低.因此,通过简化给出提钻阶段的初始条件和边界条件

其中,R为岩心半径,k=(C1−C0)/t0为边界浓度降低的速率,C1为岩心内气体初始浓度,C0为地表压力下气体的浓度,t0为岩心从井底提至地表的时间(提钻时间).

在解吸阶段,岩心内气体的浓度为提钻阶段最后时刻的气体浓度,不再是均匀分布.当岩心提至地表后,环境压力保持恒定,因此岩心的浓度边界为常数,给出解吸阶段的初始条件和边界条件

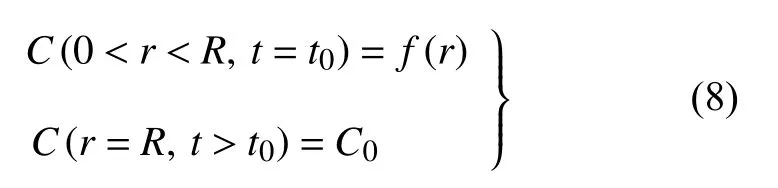
其中,f(r)为解吸过程的初始条件,可通过对提钻过程求解,得到提钻阶段的末端时刻的浓度分布,作为解 吸过程的初始条件.

1.2 提钻过程解析解

结合控制方程和提钻阶段的初始条件、边界条件,可以求解得到时间t时,页岩岩心内径向r处的气体浓度的解析解

其中, J0和 J1分别为0 阶和1 阶贝塞尔函数,R为岩心半径, αn为0 阶贝塞尔函数的第n个特征根除以岩心半径R,t为时间变量.

对式(9)进行体积分,可以计算得到圆柱岩心在时变压力边界条件下任意时刻的损失气量

如式(10)所示,在随时间变化的压力边界条件下,求解圆柱形几何形状的岩心损失气量的解析解,其函数形式与式(1)～式(3)等基于煤层气的损失气模型完全不同.

在实际工程中,式(10)所示的无限级数求和形式难以应用,考虑到 αn随着级数增加而增大,因而该无限级数为可收敛的[24-25],选取前有限项级数求和即可逼近真实结果.图3 给出了截取有限项求和所得损失气量与时间的关系,对比前100 项和500 项的求和结果(即n=100,500),二者偏差可忽略,该级数可收敛,说明可以通过截取有限项求和逼近真实结果.除此之外,还需要注意到损失气量与时间的关系为下凸函数,且在初始时刻斜率(损失气逸散速率)为0,该特性是符合实际提钻过程中气体逸散规律的.

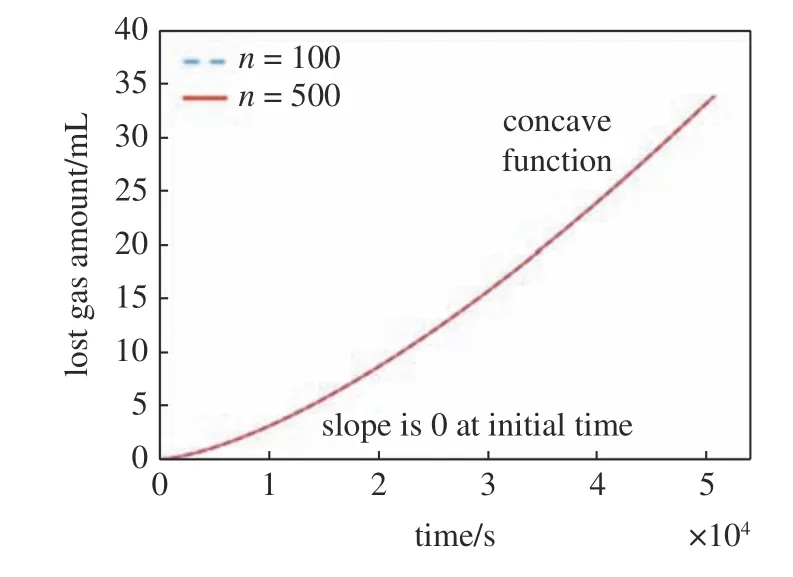
图3 截取有限项求和所得损失气量与时间的关系Fig.3 The relation between lost gas amount and time with finite terms

1.3 解吸过程解析解

在求解得到提钻阶段损失气量解析解的基础上,以提钻阶段的末期浓度分布作为解吸阶段的初始浓度分布f(r).根据解吸阶段的初始条件及边界条件,对控制方程进行求解,得到解吸阶段的浓度分布,同样地进行体积分得到解吸气量的解析解

进一步,分析解吸阶段所得解吸气量的解析解,了短时间内的解吸气量,解吸量与呈线性关系,图4(b)也可以看出解吸量与时间t的关系比较接近抛物线形式.上述为短时间的解吸结果,可以看到解吸气量最终仍未达到平衡,所以加长解吸时间,观察长时间下解吸气量与时间的关系.

图4 短时间内解吸气量与时间的关系Fig.4 The relation between desorption gas amount and time in short period

当解吸时间加长,解吸逐渐达到平衡,图5(a)的前段为短时间内的解吸过程,其与为线性关系,但随着时间增加逐渐趋于平行横坐标轴,不再是线性关系,表明解吸过程逐渐完成.图5(b)也进一步说明,解吸曲线在长时间内不再与时间t 呈抛物线关系,经典的USBM 模型不仅不适用于页岩损失气的估计,在较长的解吸时间内也不再适用[26-30].

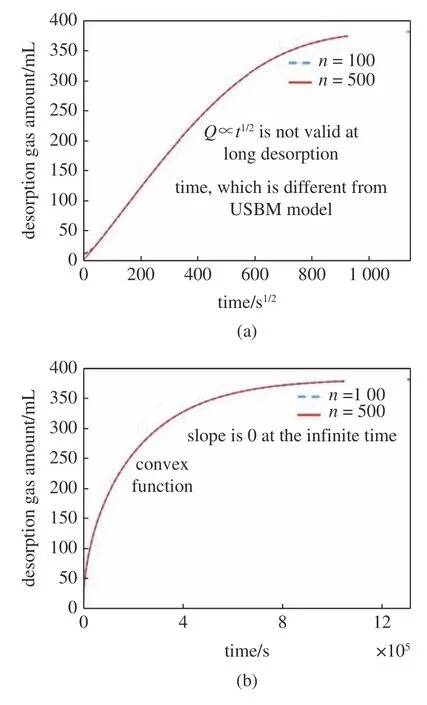
图5 长时间内解吸气量与时间的关系Fig.5 The relation between desorption gas amount and time in longperiod

将式(10)损失气量和式(11)解吸气量的解析解进行整合,图6(a)和图6(b)为全过程的页岩岩心气体逸散量与和时间t 的关系,浅蓝色虚线之前的为提钻过程中的损失气量,浅蓝色虚线之后的是解吸过程中的解吸气量.从图中可以看到,由于岩心的圆柱几何形状与时变压力边界条件的影响不可忽略,提钻过程和解吸过程的气体逸散规律完全不同.同时,可以看到提钻初始阶段,曲线的斜率为0,表示页岩损失气的逸散速率在初始阶段为0;随着岩心在井筒内的提升,内外压差越来越大,气体逸散速率增加;当岩心取至地表后,内外压差越来越小,气体逸散速率降低,可以看出该逸散规律与实际过程更为吻合,进一步证明了变边界分段模型的正确性.

图6 全过程内岩心气体逸散量与时间的关系Fig.6 The relation between escaped gas amount and time in the drifting and desorption process

2 损失气−解吸气复原实验验证变边界分段模型

2.1 实验设计

实际提钻过程中岩心内的损失气量无法通过实验测量获取,为了验证变边界分段模型的正确性,开展针对页岩岩心的损失气−解吸气复原实验[31-33],直接测量在模拟提钻过程条件下的气体逸散量和解吸过程的气体逸散量.在复原实验中,为了复现提钻过程中压力边界条件随着时间增加而线性降低的过程,采用围压阀和恒速恒压泵(ISCO 泵)控制高压饱气的岩心样品线性降压,降压时长即代表提钻时长,同时测量降压阶段的气体逸散量,代表复原实验中的损失气量.在完成降压后,继续在常压的环境压力条件下开展解吸实验,获得解吸气量与时间的关系.并在解吸曲线的基础上,采用变边界分段模型进行拟合,反推得到模型预测的损失气量,并与实验测量的损失气量对比,验证变边界分段模型的正确性.

根据相似原理,无量纲数相同的物理过程之间可进行类比.因此采用小尺寸的岩心样品复原真实岩心提钻过程的气体逸散,降压时间也相应地缩短[34-35].为了保证损失气量与解吸气量相当,方便实验测量和减小测量误差,定义如下无量纲数作为参考.

其中,t0为提钻时间(复原实验中的降压时间),D为岩心的表观扩散系数,R为岩心的半径.

通过测试之后发现,当D∗取值为0.14 时,损失气量与解吸气量相当,可以获得较好的实验测量结果,减少实验测量的误差.由于岩心样品的尺寸和表观扩散系数均为固有值,所以通过调整降压时间t0来控制损失气量与解吸气量的比例,达到减小实验误差的目的.实验所用岩心直径为2.5 cm,高度为5.0 cm,假设岩心的表观扩散系数在1.0 × 10−6～1.0 ×10−1m2/s 左右,因此复原实验需要的降压时间在20 ～2 00 s 内.

2.2 实验系统与实验方法

为了实现控制高压饱气岩心的线性降压,采用高压密封罐、回压阀和ISCO 泵进行组合控制岩心的压力边界.损失气−解吸气复原实验系统如图7 所示.岩心样品放置于高压密封的模拟罐中,该罐体内径和深度为2.6 cm 和5.1 cm,略大于岩心样品外径(2.5 cm)和高度(5.0 cm),一方面保证密封性能,另一方面也减小实验中死体积引入的测量误差.同时,将模拟罐放置在恒温水浴中,保证实验测量的恒温环境.在实验开始前,关闭模拟罐出口阀,打开进口阀与真空泵连通,通过真空泵抽出模拟罐和岩心样品中残余的空气.6 h 后断开与真空泵的连接,模拟罐的进口阀与高压气源连通,通过高压气源向岩心饱气,使得岩心样品中充满给定压力条件下的氮气,6 h 后关闭进口阀.在打开出口阀之前,通过ISCO 泵向回压阀的控压路打入略高于高压气源的压力,使得回压阀闭合.打开模拟罐出口阀与回压阀的进口端连通,此时回压阀的控压路压力(ISCO 泵压力)高于模拟罐内压力(高压气源压力),回压阀关闭.调整ISCO 泵从恒压模式改为压力梯度模式,实现线性降压,即从高压随着时间线性降低至环境压力.当ISCO 泵压力降至低于模拟罐内压力时,回压阀打开,模拟损失气段的气体流出,通过流量计量设备进行测量.当ISCO 泵压力在一段时间内降至环境压力后,仍然持续测量岩心样品中的气体逸散量,此前的气体逸散量为损失气量,此后的气体逸散量为解吸气量.

图7 损失气−解吸气复原实验系统示意图Fig.7 Schematic diagram of simulating lost gas-desorption gas experiment system

图8 为处理后的圆柱状页岩用作实验样品,直径为2.5 cm,高度为5.0 cm.经过加工后具有较为规则的外形,且与样品腔大小适配.在开始保压前已经过清洗、去除岩心内残余的杂质.

图8 损失气−解吸气复原实验的岩心样品Fig.8 Core sample used in the simulating lost gas-desorption gas experiment

2.3 实验结果验证变边界分段模型

调整初始压力(2～4 MPa) 和降压时间 (30 ～200 s),开展了若干组损失气−解吸气复原实验,测量损失气量、解吸气量与时间的曲线,采用损失气估算模型拟合解吸气段实验数据,获得外推的损失气量拟合数据,并与实验数据比对,验证模型正确性.

图9(a)～图9(c)分别为降压时间(200 s)条件下不同初始压力时,页岩样品的复原实验数据(散点)与变边界分段模型拟合结果(实线).

图9 降压时间为200 s 条件下页岩的损失气实验验证变边界分段模型Fig.9 Experimental data verified segmented variable boundary model under t0 = 200 s using shale sample

从图中可知,在实际提钻(降压)过程中的损失气段(黑色)与解吸实验(恒压)过程中的解吸气段(红色)的气体逸散规律不同,前者的气体逸散量与时间是下凸函数,而后者是上凸函数,说明前者的逸散速率(气体逸散量与时间的导数)随着时间增加是增加的,后者的逸散速率随着时间增加是减小的,这与变边界分段模型的假设完全相符,也进一步说明了已有模型假设的不真实性.从拟合结果来看,实线与散点的吻合度很高,证明了变边界分段模型的正确性.不同初始压力的实验及拟合结果均为相同规律,说明了变边界分段模型的适用压力范围较广.

USBM 模型基于经验假设认为损失气段与解吸气段具有相同的逸散规律,气体逸散量与时间是抛物线关系(与时间的1/2 次方是线性关系),也被称为线性法,是最常用的损失气估算模型.基于初始压力为3 MPa,降压时间t0为60 s 的复原实验结果,分别采用变边界分段模型和USBM 模型拟合复原实验的解吸气段实验数据,比较两种模型的拟合效果.图10 给出了二者对相同实验数据的拟合结果,其中散点为实验数据,实线为变边界分段模型的拟合结果,虚线为USBM 模型的拟合结果.从图中可知,USBM 模型在损失气段的规律(上凸函数)完全不符合实际过程的气体逸散规律(下凸函数),在解吸气段虽然与实际过程有相似性,但由于USBM 模型是抛物线函数,完全无法描述实际解吸实验中气体逸散量达到饱和的情形,所以在解吸段的吻合程度也不高.同时,由于变边界分段模型考虑了损失气段与解吸气段不同、解吸段解吸量随时间增加而逐渐饱和的逸散规律,从而取得了更好地拟合结果,显著地体现了变边界分段模型的正确性和优势.

图10 初始压力3 MPa 条件下变边界分段模型拟合结果与USBM 模型拟合结果对比Fig.10 The comparation between segmented variable boundary model and USBM model under initial pressure is 3 MPa

3 川南龙马溪组页岩储层的应用实例

3.1 地质背景

为了在实际工程中验证变边界分段模型的正确性,并与保压取心结果进行比较,采用川南地区的Y151 井作为实例.该井位于四川台坳川南低陡褶带南缘,并与滇黔北坳陷相邻,设计取心层位为志留系龙马溪组−奥陶系五峰组,其中取心深度在1699.50 ～1726.68 m 内的为常规取心段,在1727.07～1764.96 m内的为保压取心段,该井的具体参数及岩心样品的详细信息可参考文献[8].

3.2 基于常规取心的现场测试

Y151 井中共有13 组常规取心页岩样品,其中12 号和13 号样品的取心深度分别为1724.31 ～1724.58 m 和1726.40～1726.68 m,位于常规取心层段的底部,位于保压取心层段的顶部.为了方便与保压取心结果对比,所以采用12 号和13 号岩心的现场解吸实验数据,结合变边界分段模型进行拟合,其中损失气的降压时间t0假设为岩心从井底提至地表的时间的二分之一,所得结果如图11 所示.

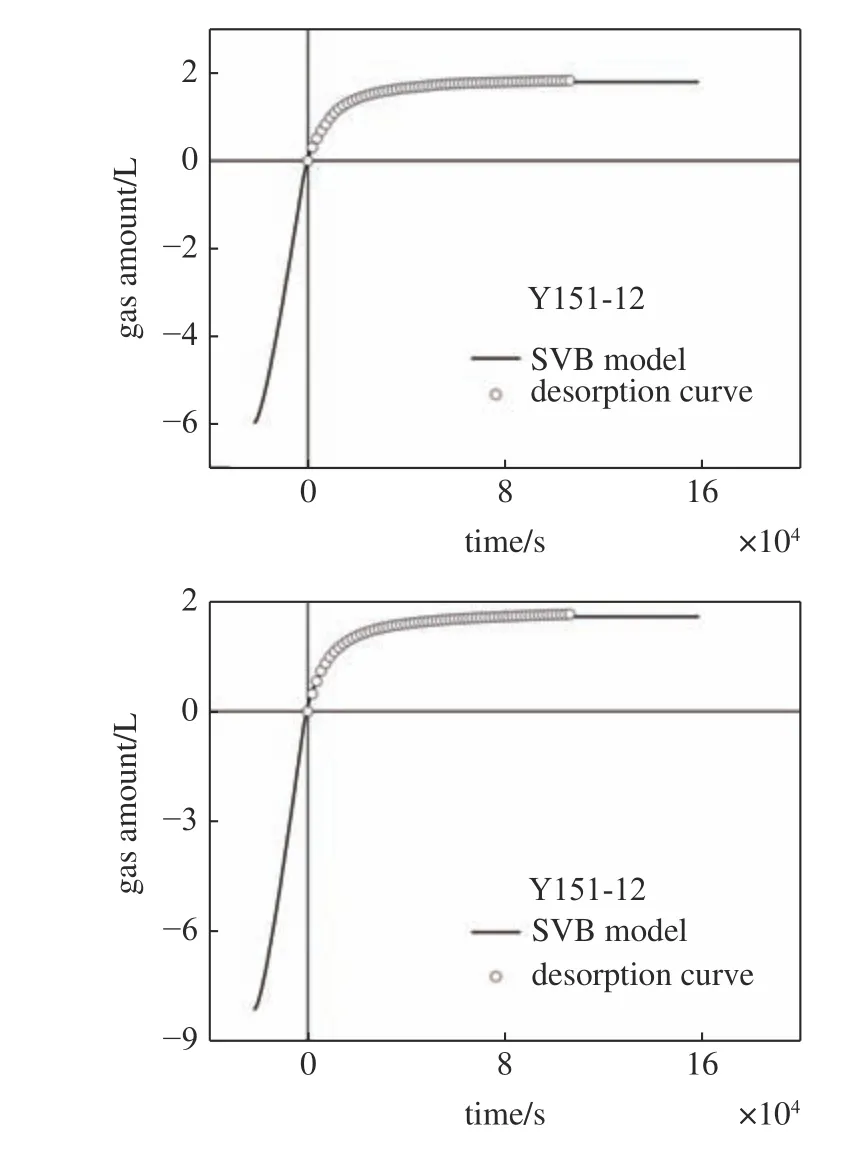
图11 川南Y151 井常规取心段代表样品现场实验解吸曲线和变边界分段模型拟合结果Fig.11 Desorption curves and the fitting results of segmented variable boundary model about conventional samples from South Sichuan Basin

从Y151 井12 号和13 号样品的现场实验数据与变边界分段模型的拟合结果可知,变边界分段模型能够较好地拟合现场实验数据.进而与保压取心结果进行对比,12 号和13 号样品的重量分别为5720 g 和5543 g,根据变边界分段模型计算得到损失气和解吸气总和分别为1.36 m3/t 和1.94 m3/t.

另外根据现场的残余气实验可知,样品残余气平均为0.10 m3/t.因而,基于常规取心的实验数据,结合变边界分段模型计算得到的12 号和13 号样品的总含气量为1.46 m3/t 和2.04 m3/t.采用保压取心的14 号样品的取心深度为1727.07～1727.33 m,与12 号和13 号样品接近,其保压取心后测量所得的含气量为2.19 m3/t.将12 号,13 号样品与14 号样品进行比较,可知常规取心结合变边界分段模型计算所得总含气量略小于保压取心测试所得总含气量,其原因主要有两方面:(1)样品总含气量受到层位深度的影响,根据更深层位保压取心实验的结果可知,在Y151 井的取心层位中,总含气量随着深度增加有增大趋势;(2)变边界分段模型的降压时间假设过小,在本研究中采用样品从井底提至地表时间的二分之一作为降压时间,但实际过程可能长于该假设.总而言之,变边界分段模型在实际工程中仍然具有良好的适用性,在未来确定更多工程细节的基础上可提高含气量的评估精度.

4 结论

本文分析了现有损失气估算方法的不足,提出了一种新的针对非常规天然气储层的损失气估算模型,并通过损失气−解吸气复原实验验证了该模型的正确性和适用性,在川南龙马溪组页岩储层评估中开展了初步应用,得到了较好的结果,结论如下:

(1)开发了变边界分段模型,该模型在预测解吸段后期时,解吸气量逐渐趋于饱和,符合岩心内气体总量有限的实际情况;在反推计算损失气段逸散规律时,损失气段初期逸散速率为零,也符合初期时岩心内外压差为零的物理实际.因此,变边界分段模型具有更好的物理真实性;

(2)在损失气−解吸气复原实验中,变边界分段模型采用全部解吸实验数据拟合所得损失气数据,与实验测量吻合良好,不存在人为选点的问题,可以排除人为操作引入的误差,具有更好的可操作性和适用性;

(3)在评估川南龙马溪组页岩储层含气量的应用中,变边界分段模型对现场数据的拟合精度高,具有良好的适用性,但由于降压时间未能通过工程现场进行测量,因而该参数的缺失影响了该模型对储层含气量的评估精度.

除此之外,变边界分段模型仍有若干可进一步发展的方面,例如提钻过程中温度边界条件的影响;变压环境中非常数扩散系数的影响;页岩纳米孔隙系统中吸附态流体与压力的非线性关系的影响;钻井液环境中水分的影响.

综上所述,本文提供了一种更为全面的页岩储层损失气量和解吸气量的评估方法,在后续的研究中有望取得更为精确的评估结果.