抗量子计算的多变量盲签名方案∗

俞惠芳,付帅凤

(西安邮电大学 网络空间安全学院,陕西 西安 7 10121)

1983年,Chaum[1]首次提出了盲签名的概念.盲签名是一种具有消息盲化特性的签名.假设消息拥有者想要签名者对待签消息进行签名,但是又不想让签名者知道待签消息的具体内容,即使以后签名者又见到了该消息签名,也不确定什么时候他签署了这个签名,这种情况下就可以用到盲签名.盲签名可以理解为将需要签名的文件放在装有复印纸的文件袋中,签名者看不到文件的具体内容,他只需要在文件袋上签名,这样签名可以通过复印纸印在文件上.盲签名主要用于电子现金支付、电子投票等需要匿名性和认证性的应用场合中[2−4].自1983年以后,盲签名引起了广泛的关注,学者们也提出了众多盲签名方案[5−7],但是目前大多数盲签名都是基于传统公钥密码体制的[8−10].传统公钥密码体制的安全性主要依赖于大整数分解问题或离散对数问题的难解性.随着量子计算[11]的发展,使得基于传统公钥密码体制的盲签名方案受到了严重威胁.为此,研究具有抗量子计算特性的盲签名方案具有重要的意义.多变量公钥密码作为后量子密码的主要候选者之一,其安全性基于有限域上二次多变量多项式方程组(multivariate quadrati c,简称MQ)问题和多项式同构(isomorphism of poly nomials,简称IP)问题的难解性,已有的量子算法目前还不能很好地解决MQ 问题和IP 问题.多变量公钥密码具有计算效率高、运算速度快等优点,非常适用于计算能力有限的设备.文献[12,13]提出了多变量环签名方案;文献[14]运用公平划分的思想,将文献[12]转化为多变量门限环签名方案;文献[15,16]提出了多变量代理签名方案;文献[17]提出了多变量群签名方案;文献[18]提出了多变量盲签名方案,但是该方案运用传统的多变量签名模型,为了产生一个有效的签名,采用了两个非满射中心映射,其只能应用在已知安全的多变量公钥密码体制下,而且安全性低、计算效率低;文献[19]提出了一个交互式的多变量盲签名方案,但是其公钥长度和签名长度较大.

2009年,Wang 等人[20]提出了一种多变量签名模型改进的方案,本质上是增加一个秘密仿射变换M来分离签名私钥和验证公钥之间的线性关系.2012年,Lu 等人[21]对Wang 等人的方案进行了分析,指出:可以通过合法用户的r+1 个已知签名建立线性方程组,使Wang 等人的方案转化为一般的签名方案,进而说明增加秘密仿射变换M并不能提高原有签名方案的安全性.Lu 等人[22]提出使用非线性可逆变换L替代秘密仿射变换M,减少签名私钥和验证公钥的线性关系,提高了签名方案的安全性.Yasuda 等人[23]提出利用非满射中心映射构造多变量公钥密码,具有隐藏代数矩阵和线性对等线性性质.

本文在盲签名和多变量公钥密码的理论基础上,借鉴文献[22]改进的多变量签名模型和文献[23]的非满射中心映射,提出一种多变量公钥密码体制下的后量子盲签名方案.由于所提方案只有一个非满射中心映射,为了使方案可以产生一个有效的签名,本文借鉴文献[24]对消息增加几个随机比特的思想.所提方案的公私钥之间没有线性关系,使得盲签名的安全性得到提高.经过安全性分析,证明了该密码方案满足盲性、不可伪造性和不可追踪性,而且计算效率高还能防御量子计算攻击.

1 预备知识

1.1 多变量公钥密码

多变量公钥密码的单向陷门函数形式是有限域F上的多变量二次多项式映射,公钥的一般形式如下:

P=(p1(x1,x2,…,xn),…,pr(x1,x2,…,xn)).

每个方程pi(i=1,2,…,r)是一个关于x=(x1,x2,…,xn)的非线性二次方程:

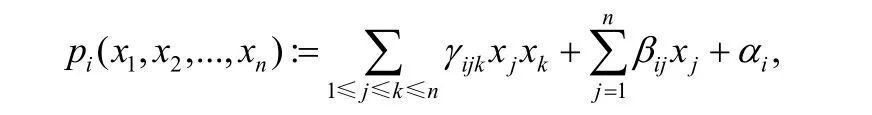
其中,方程的系数γijk,βij,αi∈F(1≤i≤n,1≤j≤k≤n),变量xj,xk∈F.多变量公钥密码的安全性主要依赖于MQ 问题和IP 问题的难解性.

定义1(MQ 问题).给定有限域Fq(q为有限域F的阶)中的r个n元方程式的非线性方程组:

p1(x1,x2,…,xn),p2(x1,x2,…,xn)=…=pr(x1,x2,…,xn)=0.

求解该方程组的问题被称为MQ 问题.已经证明MQ 问题是非确定多项式(nondeterministic polynomials,简称NP)困难问题,即使是在最小的有限域F2上.

定义2(IP 问题).设P和Q是有限域Fq上随机选取的r个n元方程的多变量方程组,且P和Q同构,则有P=T◦Q◦S,其中,T和S分别为两个可逆仿射变换,则称寻找从Q到P同构的(T,S)问题为IP 问题[16].

多变量公钥密码的签名和验证过程如下:

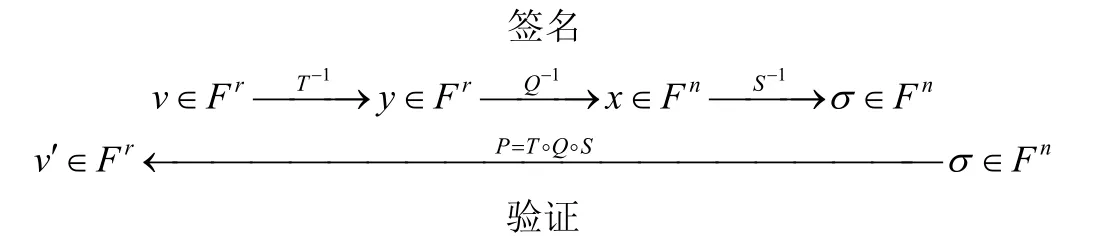
这里的S和T分别是Fn→Fn和Fr→Fr的两个可逆仿射变换,Q是Fn→Fr的中心映射,公钥为P=T◦Q◦S,私钥为{T,Q,S}.

签名:如果要对消息m进行签名,先计算消息m的哈希值v∈Fr,然后依次计算y=T−1(v)∈Fr,x=Q−1(y)∈Fn和σ=S−1(x)∈Fn,σ就是消息m的签名.

验证:如果要对签名σ进行验证,先利用公钥P=T◦Q◦S计算v′=P(σ):如果v′=v,则说明签名是有效的;否则,签名是无效的.

1.2 盲签名的形式化定义

1.2.1 算法定义

盲签名是一种具有消息盲化特性的签名,确保了签名者在不知道具体待签消息内容的情况下进行签名,即使签名者以后又见到了该消息签名,也不确定自己什么时候签署了这个签名.一个盲签名方案由以下几个算法组成.

•系统初始化:输入安全参数λ,输出系统参数;

•密钥生成:输入系统参数,输出签名者B的公私钥对;

•盲签名:该算法由如下3 个子算法组成.

(1)盲化:输入系统参数,消息拥有者O随机选取一个盲因子e,对消息m进行盲化处理,将盲化后的消息发送给B;

(2)签名:B用私钥对盲化后的消息进行签名,得到盲签名σ′;

(3)去盲化:O用B的公钥和盲化后的消息对盲签名σ′进行验证:若成立,O对盲签名σ′去盲化处理,输出最终的签名σ;否则,签名无效;

•验证:输入系统参数、消息m和B的公钥对签名σ进行验证:如果签名有效,输出1;否则,输出0.

一般地,对于消息m,如果签名者按照正确的步骤对消息m进行签名,而且在传播的过程中签名没有被篡改,那么签名σ可以通过验证.

1.2.2 安全模型

1.盲性

定义3.签名者B对消息m进行签名,但是不知道消息m的具体内容.

对于盲性的安全模型,通过游戏Game1 进行形式化定义.

Game1:敌手A(模拟签名者B)和挑战者C的盲签名交互过程如下所述.

(1)C通过运行系统初始化算法生成系统参数,同时,通过运行密钥生成算法生成签名的公私钥对,然后将系统参数和私钥发送给A;

(2)A随机选取两个等长的不同的消息m0和m1发送给C;

(3)C随机选取两个等长的不同的盲因子ec∈F和e1−c∈F,然后随机选择c∈{0,1}.最后运行盲签名中的盲化算法生成盲化消息bc和b1−c,并将bc和b1−c随机发送给A;

(4)A对bc和b1−c依次执行盲签名中的签名算法,得到盲签名cσ′和σ1′−c,并将cσ′和σ1′−c依次发送给C;

(5)C利用盲因子ec和e1−c对盲签名cσ′和σ1′−c去盲化处理,得到签名σc和σ1−c;然后,将σc和σ1−c依次发送给A;

(6)A输出一个c的猜测值c′∈{0,1}.

敌手A赢得挑战的优势为,其中,Pr(c=c′)是c=c′的概率.若敌手A以不可忽略的优势猜测正确,则挑战成功.

2.不可伪造性

定义4.对于任意的消息m,敌手A通过盲签名交互过程,成功伪造一个有效的签名并能通过验证的概率是可以忽略的.

对于不可伪造性的安全模型,通过游戏Game2 进行形式化定义.

Game2:敌手A和消息拥有者O的盲签名交互过程如下所述.

(1)O通过运行系统初始化算法生成系统参数,同时,通过运行密钥生成算法生成签名的公私钥对,然后将系统参数和公钥发送给A;

(2)O访问随机预言机,A通过公开的公钥猜测签名的私钥,与随机预言机分别进行t次盲签名交互过程,得到签名δj和σj(j=1,2,…,t);

(3)经过验证算法,签名δj和σj都验证成功.

如果敌手赢得游戏的事件用Win表示,则敌手A获胜的优势可定义为.如果等式δj=σj成立的概率可以忽略,则敌手A赢得挑战的优势可以忽略,故而盲签名具有不可伪造性.

3.不可追踪性

定义5.签名σ公布以后,即使留有当时的盲消息,签名者B也无法确定是他何时签署的.

对于不可追踪性的安全模型,通过下面Game3 进行形式化定义.

Game3:挑战者C(模拟签名者B)和消息拥有者O的盲签名交互过程如下所述.

(1)O通过运行系统初始化算法生成系统参数,同时,通过运行密钥生成算法生成签名的公私钥对,并将系统参数和私钥发送给C;

(2)O随机选取两个等长的不同的盲因子eθ和e1−θ,然后选择一个随机的比特θ∈{0,1},将消息m作为输入,执行盲签名中的盲化算法,生成盲化消息bθ和b1−θ,并将bθ和b1−θ随机发送给C;

(3)C对bθ和b1−θ依次执行盲签名中的签名算法,生成盲签名θσ′ 和σ1θ−′ ,然后将θσ′ 和σ1θ−′ 依次发送给O;

(4)O利用盲因子eθ和e1−θ对盲签名θσ′ 和σ1θ−′ 去盲化处理,得到签名σθ和σ1−θ;然后,将σθ和σ1−θ依次发送给C;

(5)C输出一个θ的猜测值θ′∈{0,1}.

挑战者C赢得挑战的优势为,其中,Pr(θ=θ′)是θ=θ′的概率.若挑战者C以不可忽略的优势猜对,则挑战成功.

1.3 Lu等人改进的多变量签名模型

Lu 等人[22]改进了Wang 等人[20]的签名模型,即把文献[20]中的秘密仿射变换M改为非线性可逆变换L,其结构如下.

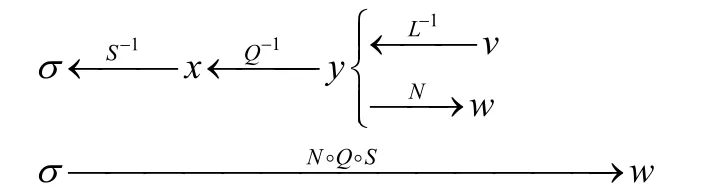
私钥:L,S和Q中的某些参数.

公钥:h◦L−1,h◦N−1和N◦Q◦S,其中,N(N≠E,N≠L)是一秘密仿射变换,E表示恒等变换,h是一个保密的单向不可逆哈希函数.

签名:设v是消息m的哈希值,依次计算y=L−1(v),x=Q−1(y)和σ=S−1(x),σ即为签名.

验证:输入公钥P=N◦Q◦S和签名σ,输出w=N◦Q◦S(σ),验证h◦L−1(v)=h◦N−1(w)是否成立:若成立,则接受签名;否则,拒绝签名.

1.4 Yasuda等人提出的非满射中心映射

设r是多变量方程组的个数,n是变量的个数.这里的r和n均为有限的正整数,并且满足n=z2,r=z(z+1)/2.Yasuda 等人[23]利用非满射来构造多变量的中心映射,具体结构如下:

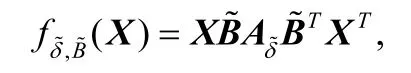
2 方案实例

本节给出了一个具体的抗量子计算的多变量盲签名方案.详细算法细节如下所述.

1.系统初始化(Setup)

生成系统参数(F,p,l,r,n,H),其中,F=GF(pl)是特征为p的有限域,r是多变量方程组的个数,n是变量的个数,哈希函数H:{0,1}*→Fr.这里的p是素数,l,r和n均为有限的正整数.

2.密钥生成(KeyGen)

生成签名者B的私钥sk:{L−1,G−1,S−1}和公钥pk:{N◦G◦S,h◦L−1,h◦N−1},公开公钥,其中,G:Fn→Fr是非满射中心映射,具体结构参照本文第1.4 节和文献[23]中的fδ,B.L:Fr→Fr是随机选取的非线性可逆变换,N和S分别是Fr→Fr,Fn→Fn随机选取的可逆仿射变换,h是一个保密的单向不可逆哈希函数.

3.盲签名(BlindSIG)

(1)对消息m增加几个随机比特m′[24];

下面介绍如何给消息m增加几个随机比特m′:

b)令m′=[W]0→2为2-bit 字符串.

(2)盲化(Blind):O随机选取盲因子e∈F,计算b=eH(m||m′),将盲化后的消息b发送给B;

(3)签名(Sign):B收到b后,用私钥sk:{L−1,G−1,S−1}依次计算y=L−1(b),x=G−1(y),若y没有与之对应的原像x,则返回步骤(1),并用H(W)替换步骤a)中的W;否则继续计算σ′=S−1(x),然后将盲签名σ′发送给O;

现在说明一下签名失败的概率:根据文献[24]的证明,对消息m增加几个随机比特m′,在签名过程中,y没有与之对应的原像x的概率约为2−85,即签名失败的概率约为2−85.这个概率是可以完全忽略不计的,因此对签名过程的效率影响可以忽略不计.

(4)去盲化(MoveBlind):O收到B的盲签名σ′后,先验证h◦N−1(N◦G◦S(σ′))=h◦L−1(b)是否成立:若成立,O对盲签名σ′去盲化处理,计算σ=σ′/e2,得到签名σ;否则,签名无效.

4.验证(Verify)

输入系统参数、消息m||m′和B的公钥,验证者计算h◦L−1(H(m||m′)),并用公钥N◦G◦S和h◦N−1验证等式h◦L−1(H(m||m′))=h◦N−1(N◦G◦S(σ))是否成立:若等式成立,则签名有效;否则,签名无效.

3 正确性分析

根据第1.2.1 节中盲签名的定义,只有合法的盲签名才能通过验证.在证明本文方案满足正确性之前,先介绍用到的相关性质.

性质1[23].若一有限域F,V是有限域F上的n维向量空间.当映射ϕ:V→F具有二次形式时,有:

ϕ(ax)=a2ϕ(x),

其中,a∈F,x∈V.

定理1.本文提出的抗量子计算的多变量盲签名方案是正确的.

证明:对消息m增加几个随机比特m′,假设对m||m′进行盲签名交互过程,可以产生一个有效的签名.若接收方收到消息m||m′的签名σ是按上述签名步骤进行的,并且在传播过程中没有被篡改,则:

h◦N−1(N◦G◦S(σ))=h◦N−1(N◦G◦S(σ′/e2))=h◦N−1(N◦G◦S(sk(eH(m||m′))/e2)).

根据性质1 可得:

sk(eH(m||m′))=e2sk(H(m||m′)).

所以,

h◦N−1(N◦G◦S(σ))=h◦N−1(N◦G◦S(sk(H(m||m′))))=h◦L−1(H(m||m′)).

可见,验证等式h◦L−1(H(m||m′))=h◦N−1(N◦G◦S(σ))成立.这说明所构造的抗量子计算的多变量盲签名方案是正确的.证毕.□

4 安全性分析

4.1 盲 性

定理2.本文提出的抗量子计算的多变量盲签名方案满足盲性.

证明:利用第1.2.2 节中的Game1 安全模型证明所提方案满足盲性.假设敌手A伪装成签名者B与挑战者C进行盲签名交互过程.

可见,敌手A无法以不可忽略的优势赢得挑战.从而证明了所构造的抗量子计算的多变量盲签名方案满足盲性.证毕.□

4.2 不可伪造性

定理3.如果IP 问题在有限域F上是困难的,那么本文提出的抗量子计算的多变量盲签名方案满足不可伪造性.

•证法1

证明:利用第1.2.2 节中的Game2 安全模型,采用反证法证明所提方案满足不可伪造性.对于一个消息m,先对消息m增加几个随机比特m′,假设对m||m′进行盲签名交互过程,可以产生一个有效的签名.以一次盲签名交互过程为例,假设敌手A成功地伪造了一个有效的盲签名δ′,同时,随机预言机产生了一个真实的盲签名σ′,并且经过消息拥有者O去盲化后,得到的签名δ和σ都能够通过验证.

(1)若δ=σ,根据去盲化过程,有:

δ′/e2=σ′/e2.

根据签名过程,有:

δ′=sk(eH(m||m′))′=e2sk(H(m||m′))′,σ′=sk(eH(m||m′))=e2sk(H(m||m′)),

则:

e2sk(H(m||m′))′/e2=e2sk(H(m||m′))/e2,sk(H(m||m′))′=sk(H(m||m′)).

若想要上式成立,那么敌手A必须得到签名者B的私钥{L−1,G−1,S−1}.由于h是一个保密的单向不可逆哈希函数,所以通过h◦L−1和h◦N−1求得L−1和N−1是不可行的,由N◦G◦S得到N−1,G−1,S−1是不可行的,这相当于解决IP 困难问题.

(2)若δ≠σ,根据去盲化过程,有:

δ′/e2≠σ′/e2.

根据签名过程,有:

e2sk(H(m||m′))′/e2≠e2sk(H(m||m′))/e2,sk(H(m||m′))′≠sk(H(m||m′)).

通过上式可知,敌手A不可能伪造一个有效的签名.

综上所述,经过t次盲签名交互过程,所得到的有效签名δj和σj都通过验证,若想要签名δj=σj(j=1,2,…,t),则必须得到签名者B的私钥{L−1,G−1,S−1}.由公钥N◦G◦S,h◦L−1和h◦L−1得到私钥{L−1,G−1,S−1},这相当于解决IP 问题.因此,敌手A无法以不可忽略的优势赢得挑战,假设不成立.从而证明了若IP 问题在有限域F上是困难的,则所构造的抗量子计算的多变量盲签名方案满足不可伪造性.证毕.□

•证法2

证明:对于一个消息m,先对消息m增加几个随机比特m′,假设对m||m′进行盲签名交互过程,可以产生一个有效的签名.分别用列表LH,LS和LV记录H询问、签名询问和验证询问,所用列表初始均为空.最多可以执行qLH次H询问、qLS次签名询问和qVL次验证询问.假设敌手A以不可忽略的优势ε成功伪造签名,则存在挑战者C以不可忽略的优势ε′解决IP 问题.

挑战者C运行系统初始化算法和密钥生成算法,将系统参数(F,p,l,r,n,H)和公钥发送给敌手A.

(1)H询问:当A向C请求关于m||m′的H询问时,首先,C查询列表LH:若LH中存在相应的记录(m||m′,H),则C直接返回结果H给A;否则,C随机选取H∈Fr发送给A,同时将(m||m′,H)添加到列表LH中;

(2)签名询问:当A向C请求关于m||m′的签名询问时,首先,C查询签名列表LS:若LS中存在相应的记录,则返回签名σ;否则,调用H询问(若在此询问之前,表中已经存在此询问记录,则伪造签名失败),再执行盲签名算法得到签名σ,然后将此记录添加到签名列表LS中;

(3)验证询问:当A向C请求关于m||m′的验证询问时,首先,C查询验证列表LV:若LV中存在相应的记录,则返回消息m||m′;否则,执行验证算法得到m||m′.再对LH进行查找:若存在相应的记录,则返回m||m′;否则,拒绝这个签名.

经过多次盲签名交互过程后,A提交一个伪造的签名σ*.

通过上面的询问,如果敌手A想要伪造一个有效的签名σ*,他必须得到签名者B的私钥{L−1,G−1,S−1}.由N◦G◦S,h◦L−1和h◦N−1得到私钥{L−1,G−1,S−1},这相当于解决IP 问题.

我们用E1和E2表示敌手A伪造签名失败的事件.

1)E1:当在步骤(2)签名询问时,重新调用的H询问已经在步骤(1)中所记录,则伪造签名失败.这个优势为:

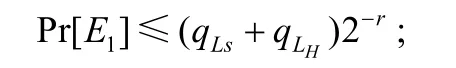
2)E2:当在步骤(3)验证询问时,拒绝了一个有效的签名.这个优势为.

因此,挑战者C解决IP 问题的优势是ε′=Pr[E1∧E2∧E3∧E4].又因为各事件之间是相互独立的,所以挑战者C解决IP 问题的优势为

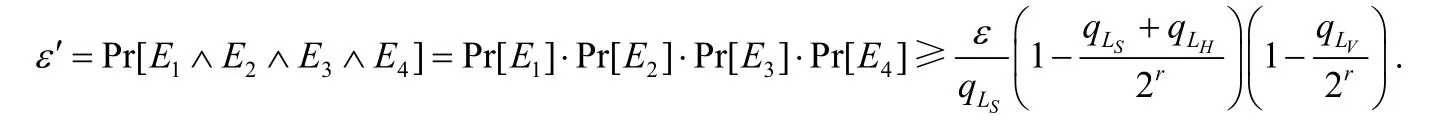
可见,挑战者C无法以不可忽略的优势ε′解决IP 问题.从而证明了如果IP 问题在有限域F上是困难的,那么所构造的抗量子计算的多变量盲签名方案满足不可伪造性.证毕.□

4.3 不可追踪性

定理4.本文提出的抗量子计算的多变量盲签名方案满足不可追踪性.

证明:利用第1.2.2 节中的Game3 安全模型证明所提方案满足不可追踪行性.下面介绍挑战者C(模拟签名者B)和消息拥有者O的盲签名交互过程.

(1)O通过运行系统初始化算法生成系统参数(F,p,l,r,n,H),同时,通过运行密钥生成算法生成签名的公私钥对,并将系统参数和私钥发送给C;

(2)对消息m增加几个随机的比特m′,假设对m||m′进行盲签名交互过程可以产生一个有效的签名;

(3)O随机选取两个等长的不同的盲因子e0∈F和e1∈F;

(4)O选择一个随机的比特值θ∈{0,1},然后计算bθ=eθH(m||m′)和b1−θ=e1−θH(m||m′),然后将bθ和b1−θ以随机顺序发送给C;

(5)C先后分别依次计算:

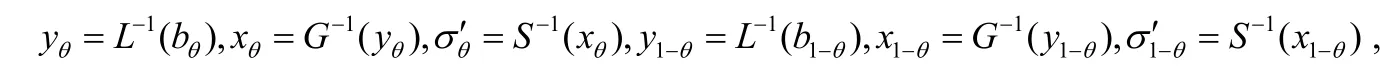
(6)O利用盲因子eθ和e1−θ计算签名和,并将σθ和σ1−θ先后发送给C;

(7)C输出一个θ的猜测值θ′∈{0,1}.

现在分析挑战者C猜对θ的概率.因为盲因子eθ和e1−θ是消息拥有者O在有限域F上随机选取的,而且选取的过程完全独立于消息m||m′,因此盲因子eθ和e1−θ、消息m||m′、签名σθ和σ1−θ这三者之间完全相互独立.对于挑战者C,在不知道盲因子的条件下,无法将消息、盲签名、签名这三者联系起来.因此,即使C拥有无限的计算能力,他猜对θ的概率只有1/2,即Pr(θ=θ′)=1/2,则挑战者C赢得挑战的优势是:

可见,挑战者C无法以不可忽略的优势赢得挑战.从而证明了所构造的抗量子计算的多变量盲签名方案满足不可追踪性.证毕.□

5 效率分析

签名效率主要取决于签名的公钥长度、私钥长度和签名长度.本节依据这3 个要素分析本文构造的抗量子计算的多变量盲签名方案与类似方案的性能.由文献[24]和L,N的构造过程可知,对消息m增加几个随机的比特m′和增加公钥h◦N−1,h◦L−1并不影响整个盲签名交互过程的运算效率.表1 从签名的公钥长度、私钥长度和签名长度分析文献[18,19]和本文方案的效率.

表1 中的r为多变量方程组的个数,n为变量的个数.从表1 可看出:由于本文方案只采用一个非满射中心映射,所以和文献[18]相比,签名的私钥长度减少了50%;与文献[19]相比,公钥长度和签名长度都有所减少.

6 结束语

目前,大多数盲签名方案都是基于传统公钥密码体制的.随着量子计算技术的发展,使得传统公钥密码体制下的盲签名受到了严重威胁.本文提出了一种基于多变量的抗量子计算盲签名方案.所提方案运用改进的多变量签名模型,采用一个非满射中心映射,将签名的公私钥分离,减少了公私钥之间的线性关系,提高了盲签名的安全性.和文献[18,19]中的方案相比,计算效率较高.通过安全性分析知,方案具有盲性、不可伪造性和不可追踪性.本文方案可应用在电子现金交易系统、匿名电子投票系统等领域.