基于层次分析法的牙齿隐形正畸方案评价与优选

李占利，党 琪，李洪安，刘童鑫，张 蕴

基于层次分析法的牙齿隐形正畸方案评价与优选

李占利，党 琪，李洪安，刘童鑫，张 蕴

(西安科技大学计算机科学与技术学院，陕西 西安 710600)

随着科学技术的发展，牙齿正畸软件系统可以自动生成若干正畸方案。针对医患如何从中选择最满意方案的问题，提出基于层次分析法的牙齿隐形正畸方案综合评价与优选方法。结合牙齿正畸医师常用的正畸标准与患者的基本需求，从咬合、美观和正畸代价3个维度考虑，建立了咬合接触情况、牙列拥挤度、牙弓对称度、牙齿移动难度、正畸周期及费用等11个指标的牙齿隐形正畸方案优选层次模型。利用层次分析法构建成对比较矩阵，通过一致性检验，确定各指标及各方案权重，计算综合权重并排序得出最优方案。结合实际案例，对不同案例进行实验，同时引入专家评分法进行实验对比，结果表明，基于层次分析法的综合评价可为医患选择牙齿隐形正畸方案提供有效参考。

牙齿正畸；层次分析法；成对比较矩阵；权重；方案优选

现如今，随着社会生活水平的提高，人们开始对健康及形象美学给予更多关注，牙齿正畸也逐渐趋于生活化。对于没有进行及时正畸错颌畸形牙齿的人群，其口腔清洁、咬合功能及面部美观会受到影响。

近年来，口腔正畸这门学科不断向计算机智能领域靠拢，隐形矫治技术[1]正快速科技化，相关领域的研究人员在隐形正畸方案这一领域做出了一定研究。2010年，杨峰[2]将牙齿移动方式进行拓展，同时引入碰撞检测对牙齿可能发生的碰撞进行检测，一定程度上提高了隐形牙齿正畸方案的治疗普遍性。张筱[3]在2016年开发了具有碰撞检测功能的隐形矫正系统，能够规划一颗牙齿运动的动态。2017年，付敬鼎[4]在牙齿自动排列方面进行了研究，通过快速搜索随机树的方法完成了牙齿运动路径的规划，能够更好地自动化生成方案。牙齿正畸方案的自动生成研究已有所成效[5]，但对牙齿正畸方案评价及优选的研究还不够成熟，医患在面对多个正畸方案进行选择时，未能快速客观地给出最终决策方案。

目前，对牙齿正畸治疗方案进行评估研究还未建立一套系统完善的评估指标框架和成熟的评估方法，更多的是医生提供方案，患者根据可承受能力进行方案选择，缺少对牙齿正畸方案的全面性研究，而牙齿正畸方案的选择由牙齿的正畸后效果、正畸费用、难度和周期等综合指标衡量。因此，牙齿正畸方案的优选本质上是多目标决策分析问题，为全面综合地考虑此类多准则并难以全部量化的问题，本文采用基于层次分析法的牙齿隐形正畸方案综合评价与优选方法。结合实例，首先根据正畸医师临床经验，通过设定评价模型中正畸因素的不同参数值，结合牙齿移动的不同路径和治疗侧重点，生成多个牙齿正畸方案，然后基于常用的3个正畸评价标准，确定正畸方案的评价指标并建立优选层次模型，最后结合患者具体情况，通过层次分析法推荐给出最佳方案。

1 牙齿正畸方案评价指标的建立

牙齿正畸是高于基础治疗标准的一项技术，其目的是为了减少健康隐患，提升口腔功能和面部美观，具体方案需要根据每个人的健康基础条件、治疗预期、个人精力以及消费能力等综合决定。

目前牙齿正畸医师常用的正畸标准主要有以下3种：Andrews正常颌六要素、PAR指数、ABO-OGS指数。其中，Andrews正常颌六要素是Andrews在1972年通过研究没有进行正畸治疗的牙颌，得出可以作为正常牙颌评判的6项标准[6]，包括：磨牙关系、轴倾角(冠角)、冠转矩(牙冠倾斜)、旋转、邻面接触和Spee曲线，该标准倾向于美观，适合原本牙齿咬合状况较好的患者；PAR指数(Peer assessment rating)，是英国正畸标准联盟在1987年公开颁发的一份关于牙颌特点的统计指数[7]，可作为正畸治疗标准指数，其主要从前牙的接触、后牙的咬合、覆盖、覆颌及中线这5方面进行评分，该标准适合牙齿存在深覆颌、深覆盖等病症的患者；1929年，美国正畸专委会(American Board of Orthodontics，ABO)设立了一种相对客观的评分体系(objective grading system，OGS)，被称为ABO-OGS指数[8]。该指数共含有：排列、咬合接触、咬合关系、咬合覆盖、边缘嵴高度、颊舌向倾斜度、邻牙接触关系和牙根平行度8个指标，其适合牙齿存在过度唇向倾斜或舌向倾斜情况的患者。

对于牙齿畸形患者而言，正畸的目标各不相同，不同患者牙齿畸形类型及程度都有差异，且各自需求不同，故在制定方案时，正畸的侧重会有所不同。本文综合集成上述3个正畸评价标准，同时结合正畸医师的从医经验，从咬合因素、美观因素以及正畸代价因素3个维度进行考虑，确定出具体的评价指标[9]。

1.1 咬合因素

牙齿最重要的功能是咀嚼功能，牙齿的紧密咬合有利于进食消食，是牙齿的关键性价值，也是患者首要考虑的因素。本文从以下3个指标确定咬合的良好程度：

(1) 咬合接触情况。正常咬合情况下，牙齿间应为交错有序，以尽可能地使咬合紧密。研究ABO-OGS标准中关于咬合的规定，需对距离进行考察，分别为：下尖牙的远端中侧与上尖牙尖端间的距离、第2下前磨牙远端中侧与第2上前磨牙侧牙尖端间的距离。若在0～1 mm范围内时，则牙齿的咬合接触优良。

(2) 深覆颌。深覆颌(垂直关系)是上牙盖住下牙的比例过大的一种牙齿畸形。正常情况下，上牙覆盖下牙的长度应在1～3 mm的范围内，超出即为深覆颌。

(3) 深覆盖。当上下前牙的水平间隙超出3 mm时，被认为是深覆盖，此为前后关系。

1.2 美观因素

外貌仪表是人际社交中的第一份“交流”，能够反映出自己的精神面貌及由内散发的气质，特别在服务行业，外表的影响更为明显。本文从以下5个指标确定牙齿的美观程度：

(1) 牙列拥挤度。牙弓的应有长度为口腔中一排牙齿的宽度相加值，牙弓的现有长度为相应牙弓线的长度。而牙列拥挤度为两者长度的差值。正常的牙颌牙列拥挤度应为1～2 mm。

(2) 牙弓对称度。牙弓对称度[10]，即上下牙列中两侧对称牙齿的对称程度。一般是通过计算左右牙齿距离牙弓中轴线的差值进行判断的。差值越小则对称度越高，仪表呈现越美观。

(3) Spee曲线深度。Spee曲线[11]是反映咬合平整度的一个指标。在口腔学中，Spee曲线深度的计算通常是计算最低牙尖端点到第2磨牙远中颊尖与中切牙最高点之间所连直线的最远距离。当Spee曲线深度在1～2 mm的范围时，该曲线平滑，即咬合良好。

(4) 颊舌向倾斜度。正常的牙齿均具有一定的倾斜程度，以保证其咬合的严紧，过大或过小均影响其咬合的功能。颊舌朝向倾斜程度的计算方法通常是求相应牙尖端距离咬合平面间的长度，合理的距离相差在1～3 mm 间。

(5) 牙齿排列。理想的牙齿姿态应该是在牙弓上排列整齐的，不应有旋转。但牙齿排列没有标准的计算方案，一般情况下，量化其旋转性是通过对牙尖连线的方向向量和理想牙弓曲线切向量间夹角的计算进行的，夹角越小，则牙齿越整齐。

1.3 正畸代价因素

在保证牙齿咬合平稳、外表姣好的前提下，患者会考虑尽可能地缩短正畸时长、减少治疗消费。本文考虑到影响正畸代价的3个指标如下：

(1) 正畸周期。对于患者，每天佩戴矫治器至少22 h，多有不便，因此正畸周期越短越好。本文使用正畸牙套数量进行评判，每个疗程一副牙套，牙套数量越少，则疗程越短，即正畸周期越短。

(2) 正畸费用。对患者而言，正畸的治疗消费越少越好。

(3) 牙齿移动难度。结合正畸医师经验，通常对隐形正畸的牙齿移动有一个难易评估，即：牙齿移动<1.0 mm时，为简单移动；牙齿需要移动1.0～2.5 mm时，为正常移动；而当牙齿需要移动2.5～3.0 mm时，被认为有点难度；若移动距离>3.0 mm，则该被认定为移动困难。

2 基于层次分析法的牙齿正畸方案优选模型

针对牙齿正畸方案的设计，要考虑众多因素，考虑因素的侧重点不同会导致方案的特性不同。而在多个方案中进行评选时，需全面客观地考虑相关因素，故所建立的优选模型应尽可能的全面客观，同时保证评选过程的相对客观。由于对隐形正畸方案的评选决策过程，所考虑因素多，且含有定性指标，满足层次分析法[12]的特征。故本文选用层次分析法完成牙齿隐形正畸方案的评价与优选。

运用层次分析法，能够有效地将原复杂的定性评价过程进行合理的量化，将无序的要素按目标层、准则层以及方案层归纳为有序的递阶层次结构[13]。

2.1 牙齿正畸方案优选的层次分析模型

确定牙齿正畸方案所需考虑的影响因素较多，且彼此之间有一定关联，本文根据正畸方案制定的决策因素，结合多位正畸医师的建议，以选择最佳的牙齿正畸方案为目标，将咬合因素、美观因素、正畸代价因素作为准则层，将细化后的咬合接触情况、牙弓对称度、正畸周期及费用等11个指标作为子准则层，对患者制定个正畸方案，基于此构建牙齿正畸方案优选的层次分析模型，如图1所示。该模型综合考虑了医师所遵循的正畸标准和患者考量因素，较为全面地覆盖到影响牙齿正畸方案的决策因素。

2.2 构造成对比较矩阵

基于建立的方案优选层次模型，对相较于上一层次不同的因子的每层因子间的相对重要性程度分别进行两两比较，建立成对比较矩阵[14]。通常按照saaty给出的9级标度来确定其相对重要性程度[15]，即将方案层中的不同影响因子相对准则层来说，分别进行两两比较，得出相应的重要性程度数值，构建成对比较矩阵。同理，得出方案层对应的成对比较矩阵。

图1 牙齿正畸方案优选层次模型

对于成对比较矩阵，若元素与的重要性之比为a，则元素与的重要性之比为a=1/a，且a=1。

2.3 层次排序及其一致性检验

层次排序是根据成对比较矩阵权重按一定顺序排列所得的指标排序。根据最大隶属度原则，得出相对权重最大值，所对应的方案便为方案层中最恰当的选择，故权向量的计算是关键。层次结构中各元素权值，可以通过式(1)计算得到[16]。对于成对比较矩阵，有

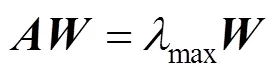
其中，max为矩阵的最大特征值；为所对应的特征向量。

为确保运用层次分析法所得评价指标的相对权重合理性，必须对成对比较矩阵进行一致性检验。一致性指标为

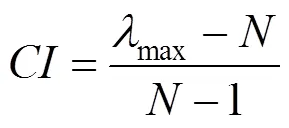
其中，为矩阵阶数。

根据一致性指标计算一致性比例，即

其中，为平均一致性指标，与有关，具体取值见表1。

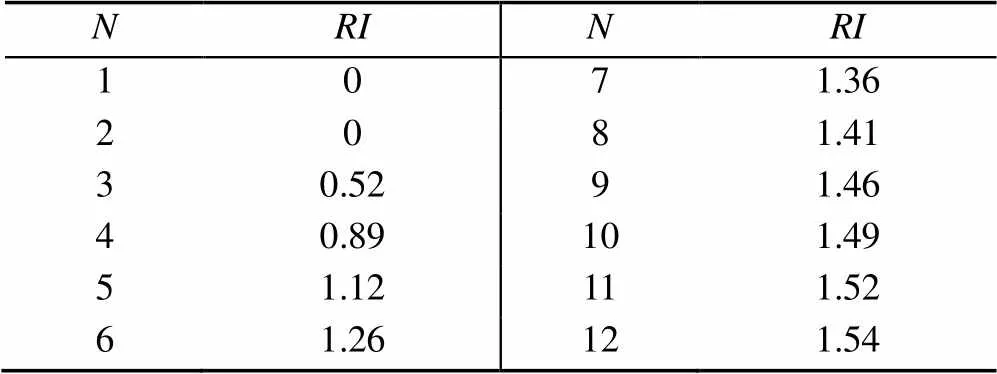
表1 平均一致性指标值

当<0.1时，认为构造的成对比较矩阵能够满足一致性要求。否则，需对其作适当的修正。

3 案例应用与分析

3.1 患者样例

患者1，女，26岁，在服务业工作，希望减少牙齿畸形带来的较大负面影响。牙齿畸形说明：安氏Ⅱ类，上方牙齿的排列存在轻度地拥挤，下方牙齿的排列存在中度的拥挤，前牙的深覆颌程度为中，深覆盖程度为中，左上切牙存在严重旋转，并伴有中度唇向倾，下切牙存在轻度内收，咬合状况良好。患者牙齿数据如图2所示。

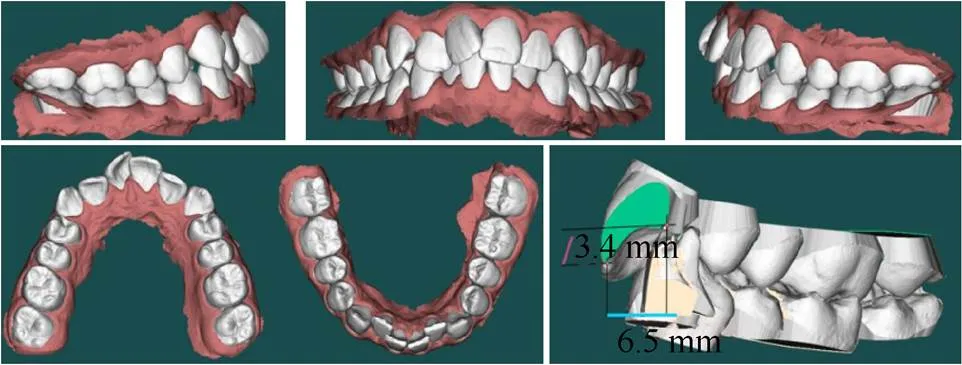
图2 样例患者牙齿数据

3.2 方案概况及对比

为患者制定牙齿正畸方案流程为：

流程1.取得所需的每一项牙齿数据，设置能够达到不同效果的3组正畸参数值；

流程2. 根据上述参数设定值及其他参数默认范围，获取3组牙齿正畸理想位姿；

流程3. 为设定的每组牙齿理想位置获得相应的牙齿移动路径集，并从中选取3条；

流程4. 生成相应的9个牙齿正畸方案。

根据牙齿正畸方案，每组理想位姿可规划选出3条路径，这些路径的正畸代价不同，但最终呈现效果相同，如图3所示。故最终疗效有3种，正畸方案可制定出9种，具体分析如下：

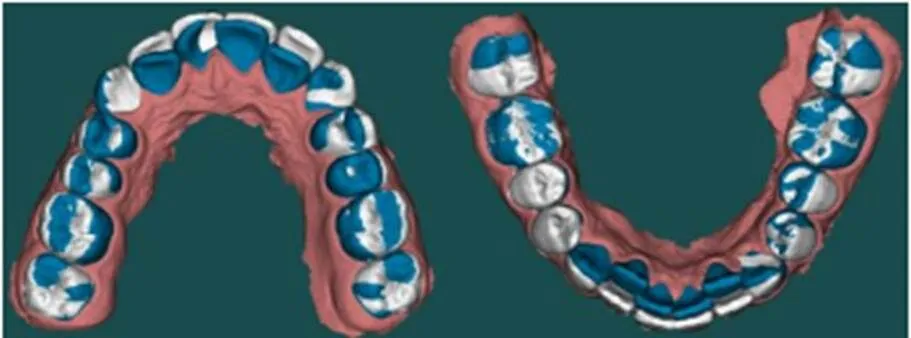
图3 正畸最终预估效果

正畸疗效一。可消除左上切牙的过度旋转，改善唇向倾；同时，改善了下切牙内收；牙齿的深覆颌和深覆盖有所改善；牙列拥挤得到改善。其缺陷为左侧上切牙产生轻微唇倾；仍存在轻度深覆颌和深覆盖。此时牙齿的理想位姿如图4所示。本文中的正畸周期均由牙齿所戴矫正器副数进行表示，对于上下两方牙齿分别用上方和下方表示，在疗效一情况下生成的3组方案为：

(1) 方案1。

周期：上方27，下方23，共50。

移动难度：较大，其中2颗移动距离超过3 mm，3颗移动距离在2.5～3.0 mm之间。

(2) 方案2。

周期：上方31，下方24，共55。

移动难度：低，其中5颗移动距离在2.5～3.0 mm之间。

(3) 方案3。

周期：上方30，下方25，共55。

移动难度：正常，其中1颗移动距离超过3.0 mm，3颗移动距离在2.5～3.0 mm之间。

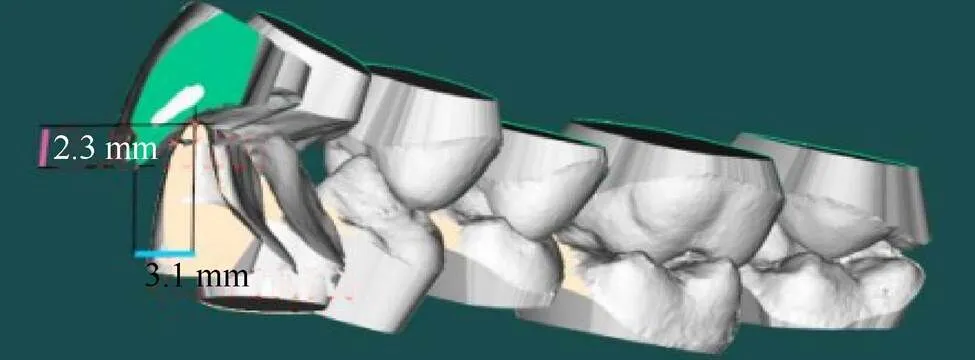
图4 方案1～3的牙齿理想位姿

正畸效果二。消除左上切牙的过度旋转，改善唇倾；改善下颌切牙内收；消除深覆颌和深覆盖。其缺陷为没有改善牙列的拥挤程度；牙列的美观效果不佳。此时牙齿的理想位姿如图5所示。所生成的3组方案为：

(1) 方案4。

周期：上方22，下方20，共42。

移动难度：低，其中2颗移动距离在2.5～3.0 mm之间。

(2) 方案5。

周期：上方18，下方19，共37。

移动难度：高，其中3颗移动距离超过3.0 mm，2颗移动距离在2.5～3.0 mm之间。

(3) 方案6。

周期：上方20，下方21，共41。

移动难度：正常，其中4颗移动距离在 2.5～3.0 mm之间。

图5 方案4～6的牙齿理想位姿

正畸效果三。消除了左侧上切牙的过度旋转，消除了唇倾；消除了下切牙的内收；消除了深覆颌和深覆盖；消除了牙列拥挤。其缺陷为正畸的周期长，费用较为昂贵。此时牙齿的理想位姿如图6所示。所生成的3组方案为：

(1) 方案7。

周期：上方33，下方27，共60。

移动难度：低，其中没有牙齿移动困难。

(2) 方案8。

周期：上方30，下方24，共54。

移动难度：正常，其中2颗移动距离在 2.5～3.0 mm之间。

(3) 方案9。

周期：上方34，下方24，共58。

移动难度：正常，其中3颗移动距离在 2.5～3.0 mm之间。

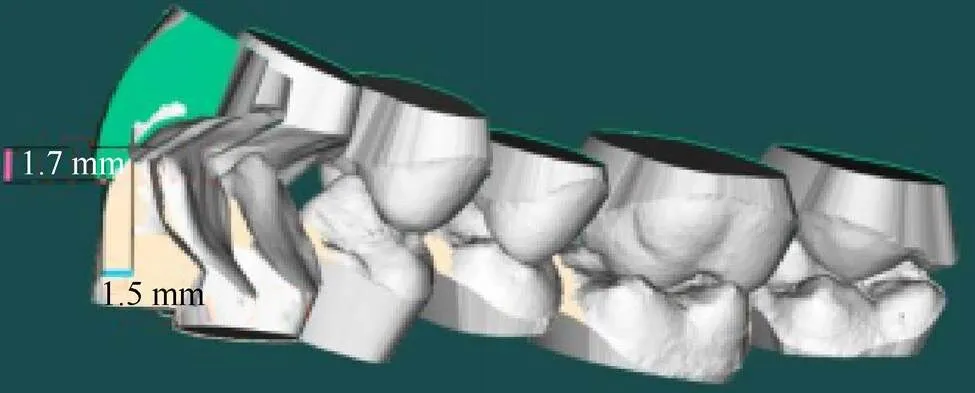
图6 方案7～9的牙齿理想位姿

3.3 方案优选

基于牙齿正畸方案优选层次模型，建立各指标成对比较矩阵，进而得到相应的指标权重。为确保分析结果的准确性，本文选择由多个正畸医师对子准则层1～11进行打分评价取平均值，得到子准则层各指标间两两对比的重要度判断，构造得到判断矩阵为，并计算得到相应权重w=[0.3006, 0.1576, 0.1576, 0.0775, 0.0595, 0.0644, 0.0567, 0.0647, 0.0170, 0.0170, 0.0302]，以及

此时，根据式(1)～(3)对判断矩阵进行一致性检验，可得：max=11.5857，=0.0586，且由表1可得对应的值为1.52，计算得=0.0385<0.1，故通过了一致性检验。

表2 方案对比

根据各方案的对比情况，建立方案层对子准则层各指标的成对比较矩阵，即相对于子准则层中的某一元素，方案1～9进行两两对比，得出相对于该指标各方案间的相对重要程度值。针对咬合接触情况这一指标，构建成对比较矩阵，即

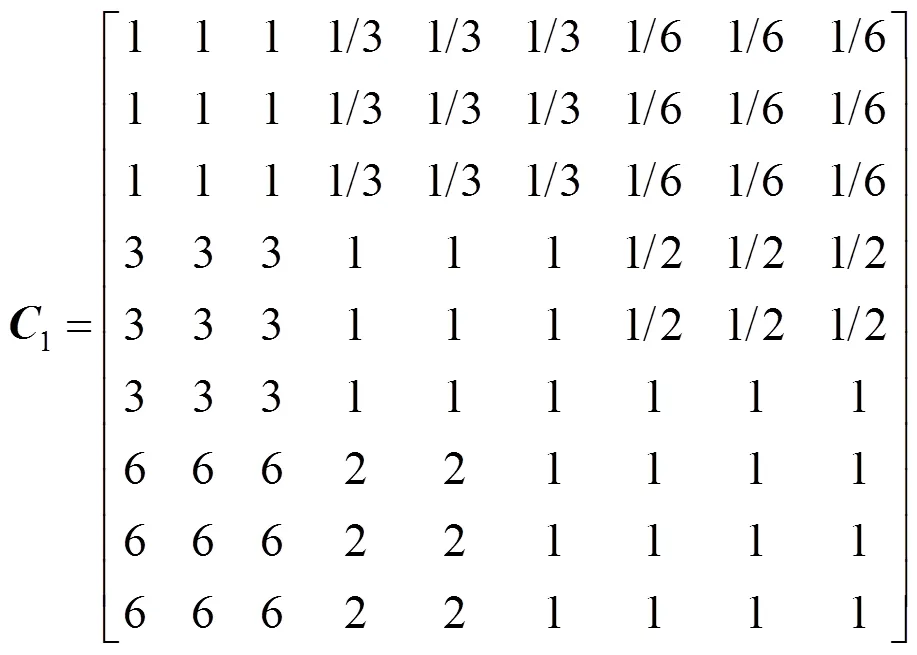
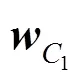
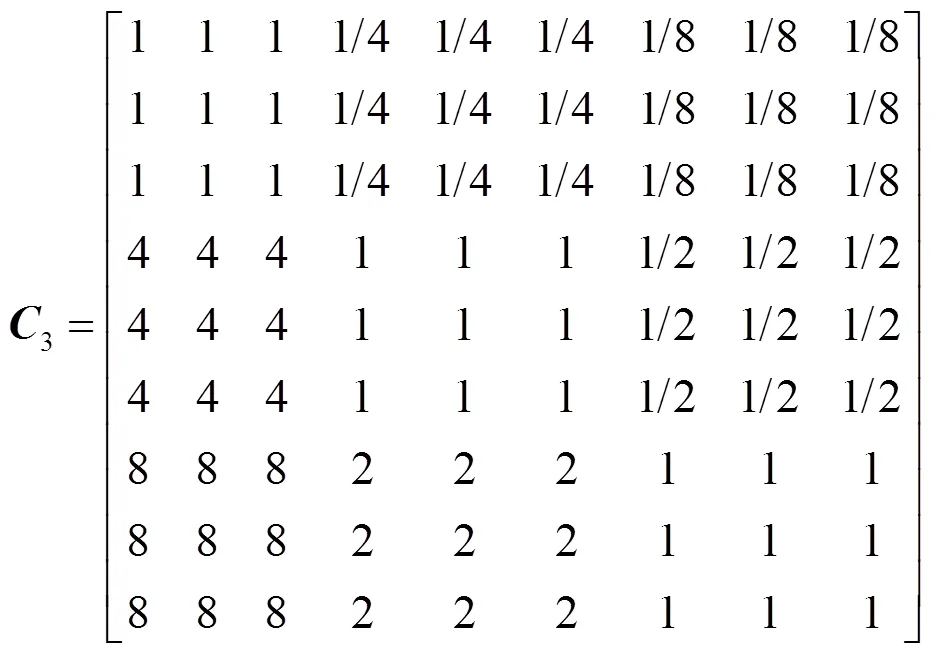
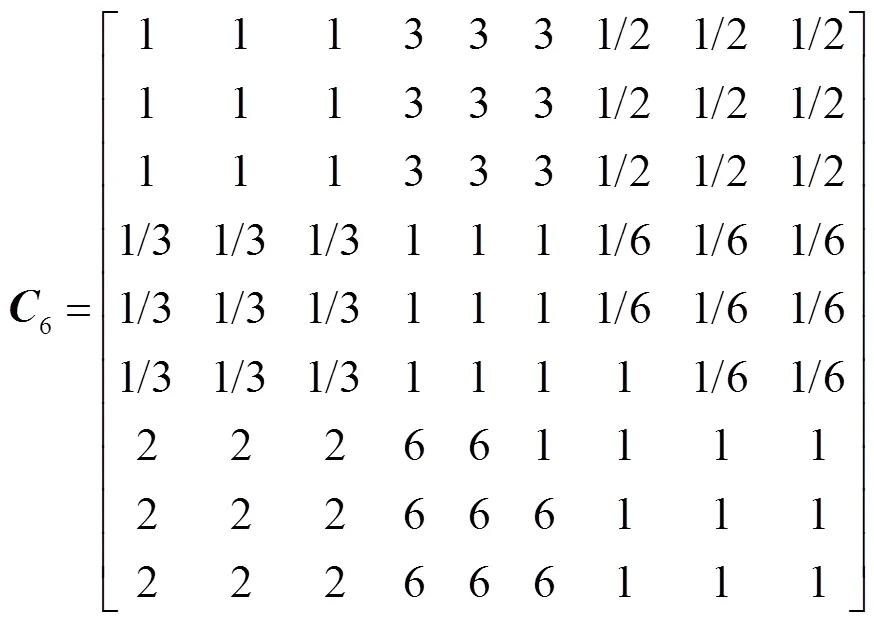
表3 方案层对子准则层各因素的相对权重

根据最大隶属度识别原则，基于综合权向量结果进行排序，即得0.1873>0.1868>0.1864>0.0999> 0.0943>0.0898>0.0506=0.0506>0.0543，其中0.1873对应方案8，故得出在9个方案中，方案8为最优正畸方案。

同时，针对该患者的牙齿情况向5位医师进行问卷调查，问卷内容主要是对9个方案分别从牙齿正畸层次模型所考虑的因素展开，对各因素进行打分，1～10分，分数越高则相对难度越大或代价越高。即得分与方案优劣呈反比。对5位医师的问卷调查反馈表进行整理归纳，并计算调查反馈表中各医师所给出评分的均值，结果见表4。

表4 专家问卷调查后所得评分均值表

从表4可以得出，在现有的9个方案中，5位医师给出的评分均值最低的方案为方案8，故专家评分法得出最适合的方案为方案8。其与本文层次分析法所选最优方案一致，故层次分析法适用于牙齿正畸方案的优选，且基于层次分析法的牙齿正畸方案既考虑了医生的医疗标准，又考虑了患者的基本需求，较为全面综合地对牙齿正畸方案进行优选，计算简便，结果清晰。

3.4 其他案例

基于提出的运用层次分析法的牙齿隐形正畸方案与优选，对另一患者进行验证。

患者2，男，19岁，其牙齿数据如图7所示。患者需求为修复咬合情况，尽量维持美观。

诊断：安氏Ⅱ类，咬合接触较差，上牙列不够整齐、尖牙咬合的接触情况较差、前牙存在轻度深覆盖，下牙列存在拥挤情况，右尖牙旋转严重。

治疗计划：改善咬合状态；消除深覆盖，调整上右切牙；消除牙列拥挤，确保上下牙列整齐舒适；改善右尖牙旋转状态。

正畸最终呈现效果如图8所示。

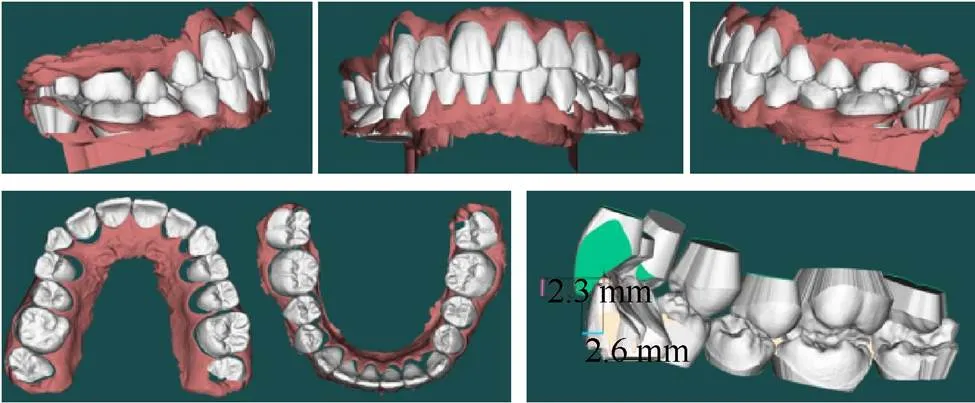
图7 患者牙齿数据

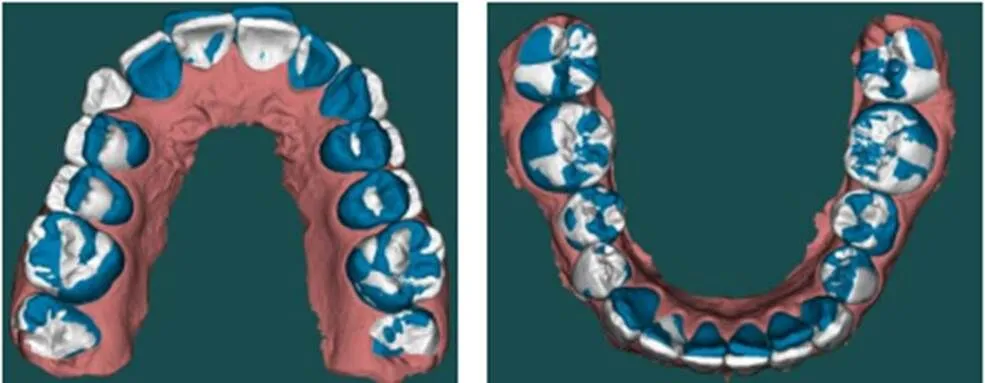
图8 患者牙齿正畸前后对比图

根据方案生成步骤，同样生成9种方案，分别如下：

(1) 方案1。

周期：上方20，下方27，共47。

移动难度：低，其中2颗移动距离在1.0～2.5 mm之间。

(2) 方案2。

周期：上方19，下方26，共45。

移动难度：较大，其中2颗移动距离超过3.0 mm，3颗移动距离在2.5～3.0 mm之间。

(3) 方案3。

周期：上方24，下方33，共57。

移动难度：正常，其中1颗移动距离超过3.0 mm，2颗移动距离在2.5～3.0 mm之间。

(4) 方案4。

周期：上方23，下方27，共50。

移动难度：低，其中3颗移动距离在2.5～3.0 mm之间。

(5) 方案5。

周期：上方18，下方31，共49。

移动难度：高，其中3颗移动距离超过3.0 mm，2颗移动距离在2.5～3.0 mm之间。

(6) 方案6。

周期：上方20，下方30，共50。

移动难度：正常，其中3颗移动距离在2.5～ 3.0 mm之间。

(7) 方案7。

周期：上方24，下方36，共60。

移动难度：低，没有牙齿移动困难。

(8) 方案8。

周期：上方21，下方30，共51。

移动难度：正常，其中2颗移动距离在2.5～ 3.0 mm之间。

(9) 方案9。

周期：上方25，下方34，共59。

移动难度：低，其中仅1颗移动距离在2.5～ 3.0 mm之间。

运用牙齿正畸方案优选层次模型，结合患者治疗需求，建立各层次因素的成对比较矩阵，对于目标层的各因素成对比较矩阵，现对患者2的9种方案对于准则层分别建立成对比较矩阵1,2,···,11进而得到各层次的指标权重见表5，计算综合权重过程。

根据最大隶属度识别原则，基于综合权向量结果进行排序，即得出在为患者制定的9个方案中，方案5为推荐的最优正畸方案。

针对不同患者，基于该牙齿正畸方案优选层次模型，可以为患者在已有方案中高效准确地选择最满意的正畸方案。

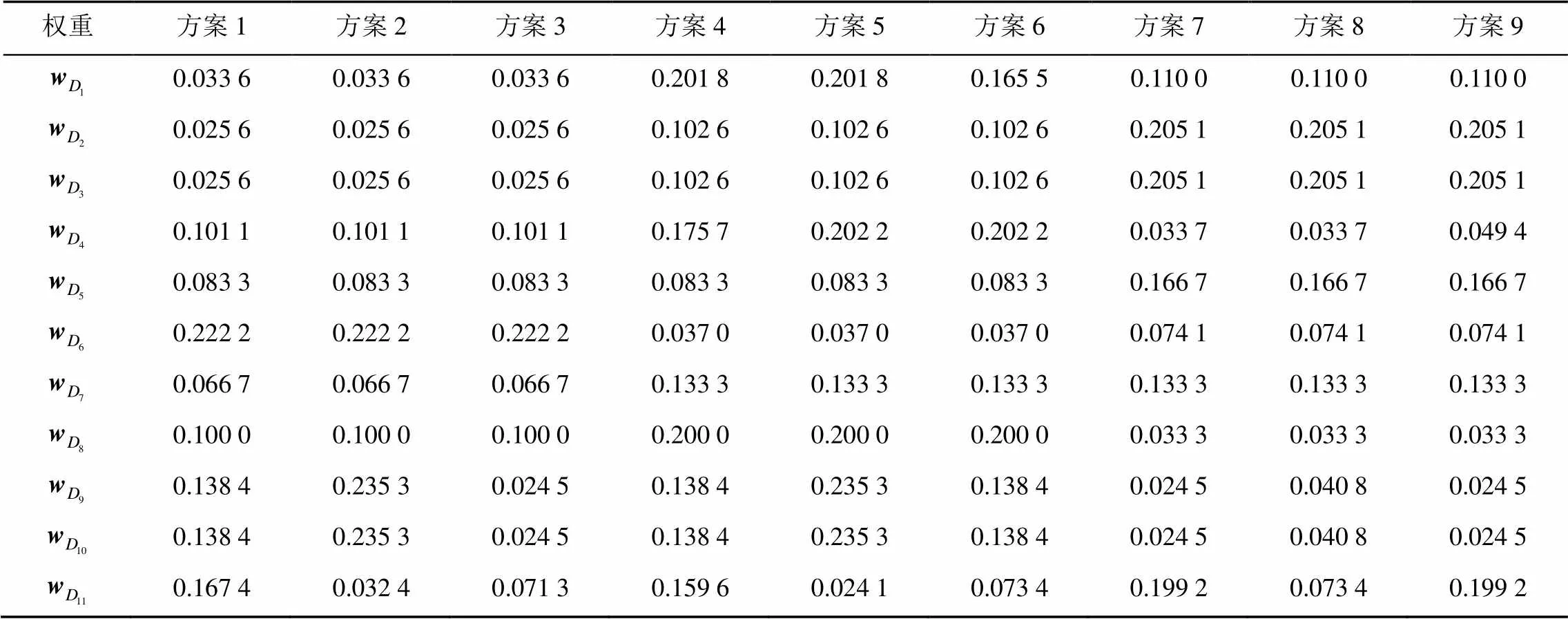
表5 方案层对子准则层各因素的相对权重

4 结 论

对牙齿隐形正畸方案综合评价及选择所建立的指标体系，从咬合因素、美观因素以及正畸代价因素3个维度选择了包括咬合接触情况、覆颌、覆盖、Spee曲线深度、牙列拥挤度、牙弓对称度、颊舌向倾斜度、牙齿排列、正畸周期、正畸费用和牙齿移动难度的11个指标，全面考虑了选择牙齿正畸方案的影响因素，对医患选择牙齿正畸方案有一定实用性。

结合实际案例，针对患者具体情况，根据正畸方案生成流程，综合考虑评价标准中的指标范围及患者正畸的可能需求，制定出牙齿正畸预选方案。运用层次分析法计算出多个正畸方案的最终综合权重，得出所占权重最高的方案8，即选出的最优方案为方案8。所得结果与专家问卷调查结果相符，且可以明确得出咬合因素、美观因素以及正畸代价因素中哪些因素所占影响力度较大。同时对另一患者的9种方案进行比选，验证得出，对于不同患者，该方法均可对所生成方案进行比较，量化评价结果进而得出最满意方案，故基于层次分析法对牙齿隐形正畸方案的预选方案进行综合评价，能够便捷有效地帮助医患从若干方案中选择并确定一个最满意的方案。

[1] 厉松, 苏茹甘. 数字化技术在口腔正畸临床中的应用[J]. 口腔疾病防治, 2019, 27(2): 69-73.

LI S, SU R G. Application of digital technology in orthodontic clinic[J]. Journal of Prevention and Treatment for Stomatological Diseases, 2019, 27(2): 69-73 (in Chinese).

[2] 杨峰. 牙齿隐形正畸系统的研究与实现[D]. 杭州: 浙江大学, 2010.

YANG F. Invisible orthodontic treatment system[D]. Hangzhou: Zhejiang University, 2010 (in Chinese).

[3] 张筱. 牙齿正畸路径规划方法研究及可视化开发[D]. 济南: 山东大学, 2016.

ZHANG X. Research on teeth orthodontic movement path planning and visual development[D]. Jinan: Shandong University, 2016 (in Chinese).

[4] 付敬鼎. 隐形矫治技术中的正畴路径规划研究[D]. 西安: 西安科技大学, 2018.

FU J D. Research on the path planning for orthodontics in invisalign technique[D]. Xi'an: Xi'an University of Science and Technology, 2018 (in Chinese).

[5] 焦韦蓉, 李雅彬. Insignia 矫治系统在正畸治疗中的应用研究进展[J]. 人民军医, 2020, 63(12): 1240-1243.

JIAO W R, LI Y B. Application research progress of Insignia correction system in orthodontic treatment[J]. People’s Military Surgeon, 2020, 63(12): 1240-1243 (in Chinese).

[6] ANDREWS L F. The six keys to normal occlusion[J]. American Journal of Orthodontics, 1972, 62(3): 296-309.

[7] 王英男, 常乐, 刘红彦. 应用PAR指数评价80例患者正畸治疗效果的影响因素分析[J]. 实用口腔医学杂志, 2016, 32(2): 263-267.

WANG Y N, CHANG L, LIU H Y. Peer assessment rating analysis of the influencing factors of treatment outcomes of 80 cases underwent orthodontic therapy[J]. Journal of Practical Stomatology, 2016, 32(2): 263-267 (in Chinese).

[8] 轩亚茹, 吕瑾茹, 刘洋, 等. 隐形矫治器对成人错(牙合)畸形患者牙周指数及ABO-OGS评分的影响[J]. 中国医疗美容, 2020, 10(11): 95-100.

XUAN Y R, LYU J R, LIU Y, et al. The effect of invisible appliance on the periodontal index and ABO-OGS score of adult patients with malocclusion[J]. China Medical Cosmetology, 2020, 10(11): 95-100 (in Chinese).

[9] 刘童鑫. 隐形矫治系统中正畸方案自动生成方法研究[D].西安: 西安科技大学,2020.

LIU T X. Research on automatic generation method of orthodontic plan in invisible correction system[D]. Xi’an: Xi’an University of Science and Technology, 2020 (in Chinese).

[10] 聂琼, 林久祥. Angle各类错(牙合)及正常(牙合)牙弓对称性分析与比较[J]. 中华口腔医学杂志, 2000, 35(2): 105-107.

NIE Q, LIN J X. Analysis and comparison of arch symmetry of various malocclusion and normal (occlusion) angle[J]. Chinese Journal of Stomatology, 2000, 35(2): 105-107 (in Chinese).

[11] 龚诚, 闻娟, 李佳岭, 等. Spee曲线和拥挤度对口腔正畸模型2D与3D测量法的影响[J]. 口腔医学研究, 2018, 34(6): 657-661.

GONG C, WEN J, LI J L, et al. Influence of spee’s curve and crowding on 2D and 3D measurement of orthodontic model[J]. Journal of Oral Science Research, 2018, 34(6): 657-661 (in Chinese).

[12] 张炳江. 层次分析法及其应用案例[M]. 北京: 电子工业出版社, 2014: 36-78.

ZHANG B J. AHP and its application cases[M]. Beijing: Publishing House of Electronics Industry, 2014: 36-78 (in Chinese).

[13] SHARMA D, SRIDHAR S, CLAUDIO D. Comparison of AHP-TOPSIS and AHP-AHP methods in multi-criteria decision-making problems[J]. International Journal of Industrial and Systems Engineering, 2020, 34(2): 203.

[14] REIG-MULLOR J, PLA-SANTAMARIA D, GARCIA- BERNABEU A. Extended fuzzy analytic hierarchy process (E-FAHP): a general approach[J]. Mathematics, 2020, 8(11): 1-14.

[15] 王晓形. 基于AHP及专家打分法的大跨度隧道风险评估[J]. 现代隧道技术, 2020, 57(S1): 233-240.

WANG X X. Risk assessment of the large-span tunnel based on AHP and expert scoring method[J]. Modern Tunnelling Technology, 2020, 57(S1): 233-240 (in Chinese).

[16] 娄亮杰, 林竹, 刘苒, 等. 基于层次分析法的储罐外涂层老化评价研究[J]. 表面技术, 2020, 49(12): 305-310.

LOU L J, LIN Z, LIU R, et al. Aging evaluation of outer coating for storage tank based on analytic hierarchy process[J]. Surface Technology, 2020, 49(12): 305-310 (in Chinese).

Evaluation and optimal selection of invisible orthodontic schemes based on analytic hierarchy process

LI Zhan-li, DANG Qi, LI Hong-an, LIU Tong-xin, ZHANG Yun

(College of Computer Science and Technology, Xi’an University of Science and Technology, Xi’an Shaanxi 710600, China)

With the development of science and technology, the dental orthodontic software system can automatically generate several orthodontic schemes. Aiming at the problem of how to help doctors and patients choose the most satisfactory scheme, a comprehensive evaluation and selection method for the invisible orthodontic scheme based on the analytic hierarchy process was proposed. In light of the orthodontic standards commonly used by orthodontists and the basic demands of patients, this paper proposed a hierarchical model for selecting the best invisible orthodontic scheme. The model took into account such three dimensions as occlusion, aesthetics, and orthodontic costs, and encompassed eleven orthodontic indicators, such as occlusion contact, crowding degree of dentition, dental arch symmetry, tooth movement difficulty, orthodontic cycle, and cost. The analytic hierarchy process was utilized to construct a paired comparison matrix, pass the consistency test, determine the weight of each index and each program, calculate the comprehensive weight, and conduct the sorting, thusobtaining the optimal program. Based on case studies, the paper conducted experiments on different cases, and resorted to the expert scoring method for experimental comparison. The results show that the comprehensive evaluation based on the analytic hierarchy process can provide an effective reference for doctors and patients to choose an appropriate invisible orthodontic scheme.

orthodontic; analytic hierarchy process; pairwise comparison matrix; weight; optimal selection of scheme

TP 391；TB 472

10.11996/JG.j.2095-302X.2021050856

A

2095-302X(2021)05-0856-10

2020-12-15；

2021-03-02

15 December，2020；

2March，2021

陕西省自然科学基础研究计划项目(2020JQ-758，2019JM-162)，企业-陕煤联合基金项目(2019JLM-10)

Natural Science Basic Research Plan in Shaanxi Province (2020JQ-758, 2019JM-162), Enterprise-Shaanxi Coal Joint Fund Project (2019JLM-10)

李占利(1964-)，男，陕西周至人，教授，博士，博士生导师。主要研究方向为计算机图形图像处理。E-mail：lizl@xust.edu.cn

LI Zhan-li (1964-), male, professor, Ph.D. His main research interests cover computer graphics, image processing. E-mail：lizl@xust.edu.cn

李洪安(1978-)，男，山东武城人，副教授，博士，硕士生导师。主要研究方向为计算机图形图像处理。E-mail：an6860@126.com

LI Hong-an (1978-), male, associate professor, Ph.D. His main research interests cover computer graphics, image processing.E-mail：an6860@126.com