基于FDM与FAHP的儿童滑板车设计评价与改进

王志愿，戴志鹏

基于FDM与FAHP的儿童滑板车设计评价与改进

王志愿1,2，戴志鹏3

(1. 安徽理工大学机械工程学院，安徽 淮南 232001；2.安徽理工大学省部共建深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；3. 安徽理工大学化学工程学院，安徽 淮南 232001)

儿童滑板车设计评价的影响因素复杂多样，难以通过量化的方法衡量这些因素对于产品设计的重要性。采用模糊德尔菲法(FDM)定量地筛选产品设计评价指标要素，建立儿童滑板车设计层级指标模型。然后，运用模糊层次分析法(FAHP)计算出各项指标要素权重，综合评价设计方案，得出儿童滑板车总体评价分值，最终提出优化与改良意见。FDM与FAHP结合可以较为系统地对产品进行量化设计与评价，减少设计过程中的主观因素，使设计更加科学、理性与严谨，也为儿童产品设计方案的选择和优化提供了可量化的参考依据。

工业设计；儿童滑板车；模糊德尔菲法；模糊层次分析法；设计评价指标

儿童滑板车具有益智性、便携性和美观性等优点，越来越受到儿童和家长的青睐。近年来，一些学者对儿童滑板车的研究也日益兴起，如胡珊等[1]基于用户动态需求的产品迭代创新设计方法对儿童滑板车进行创新设计；杨静[2]基于AHP-TRIZ理论对儿童滑板车进行创新设计；韩鹏[3]提出了儿童滑板车情感化设计过程和方法。目前这些研究缺乏对产品进行系统的量化设计与分析。设计方案评价指标的筛选与构建过于主观，缺少可量化的参数指导，无法保障设计评价指标框架的科学性与合理性。模糊德尔菲法(fuzzy Delphi method，FDM)提供了一种处理复杂设计评价指标模型构建的方法。其是将模糊理论与传统的德尔菲法(Delphi method，DM)相结合的方法，有效地减少研究的时间和成本，以及行业专家评论的模糊不确定性[4]。模糊层次分析法(fuzzy analytic hierarchy process，FAHP)是将层次分析法(analytic hierarchy process，AHP)和模糊数学结合的一种求取各项评估指标权重关系与重要性程度的综合量化方法，可有效地帮助决策者在特定问题的层次框架下做出更合理的评估[5]。FDM与FAHP相结合，可以让多指标、多因素的评价问题更系统化与科学化，已被广泛应用于不同领域的评估、标准化和标准的选择[6-9]。SHAHBOD等[10]采用FDM和FAHP建立城市医疗中心环境绩效评价模型；KANG等[11]利用FDM来筛选家用健身车产品的项目指标，开发满意客户需求的产品形态；LIN[12]在时装设计方案评估系统中应用FDM与FAHP确定标准权重；雷磊[13]采用FAHP和FDM对生物技术产业的发展与成功起关键作用的因素进行了筛选；董文丽等[14]通过FDM优化了历史文化名城保护规划实施评价研究的框架体系。但是，很少有文献将FDM的应用涉及到儿童产品设计领域。因此，本文提出将FDM与FAHP相结合的方法，构建科学合理的设计方案评价体系，为儿童产品设计提供具体的参数指导。通过FDM定量地筛选产品的设计评价指标，评估各项指标的重要性层级，建立层级指标模型，保证指标体系的科学性与合理性。然后运用FAHP从定性与定量2个层面对指标权重计算与排序，并对设计方案进行综合评价，得出总体评价分值，最终提出优化与改良意见。本文以儿童滑板车为研究案例，对该方法进行了可行性验证，并针对后续改良提出了有效性的建议。具体的研究思路框架如图1所示。

图1 研究思路框架

1 基于FDM的设计评价指标的筛选

DM最早是由美国公司RAND在19世纪50年代后期提出的。传统的DM是一种行业专家意见调查方法，但在许多情况下专家判断不能被精确地解释定量值，因此有学者提出用模糊理论来解决上述存在的问题。FDM是由MURRAY等[15]提出的，ISHIKAWA等[16]利用累积次数分配与模糊积分的概念，将行业专家意见整合为模糊数，确定了FDM。本文采用模糊数的“灰色地带检验法”，并应用了文献[17-18]提出的程序。

1.1 分析调查问卷

通过调查问卷，构建儿童滑板车设计的评价指标模型：①收集影响儿童滑板车设计评价的一级及二级准则层的指标因素，并由行业专家确定准则层指标因素；②通过FDM对调查问卷进行分析与计算，当专家意见趋于一致且达到收敛状态时，问卷调查结束。否则，将行业专家意见和修改后的问卷反馈给被访对象，直到所有指标均通过一致性检验[19]；③设定门槛值，筛选评价指标，最终确定儿童滑板车设计评价指标模型。

在对儿童滑板车设计评价分析中，将用户对其需求作为设计评价指标要素，即该产品需要满足儿童使用产品时的安全性、实用性、美观性的同时，也要满足家长对于平衡车可促进儿童智力等全方位发展的需求。儿童滑板车的目标年龄段为1～6岁。对产品进行多次实地调研，记录儿童骑行滑板车的行为过程，并查阅相关文献资料，挖掘影响儿童滑板车设计的因素。通过多轮DM，对调研后收集的资料和评价指标因素进行讨论，并经专家确定得到儿童滑板车设计评价的一级准则层的评价指标4项，即安全性、实用性、美观性、发展性和二级准则层的评价指标19项，即结构、材料、稳定、功能、人机、易用、便携、经济、形态、色彩、工艺、装饰、技术、教育、益智、互动、趣味、可持续、环保，因指标因素较多，传统的DM不能客观地确定。本文利用FDM对19项二级准则指标因素进行科学定量的筛选及打分，打分采用0～10个等级，指标因素所得分数越高表示越重要。根据行业专家问卷反馈，统计其对二级每一项评价指标的“重要性程度可接受的最小值及最大值”的赋值并进行分析，将处在2倍标准差以外的极端数据剔除。最小值表明该行业专家对该评价指标的保守认知值，以C表示。最大值则表明该行业专家对该评价指标的乐观认知值，以O表示。分数越高，则表明该评价指标越重要。采用双三角模糊数法对儿童滑板车设计的19项二级评价指标进行分析，利用“灰色地带定检法”检验收敛性，优选出其二级评价指标。

1.2 建立双三角模糊数

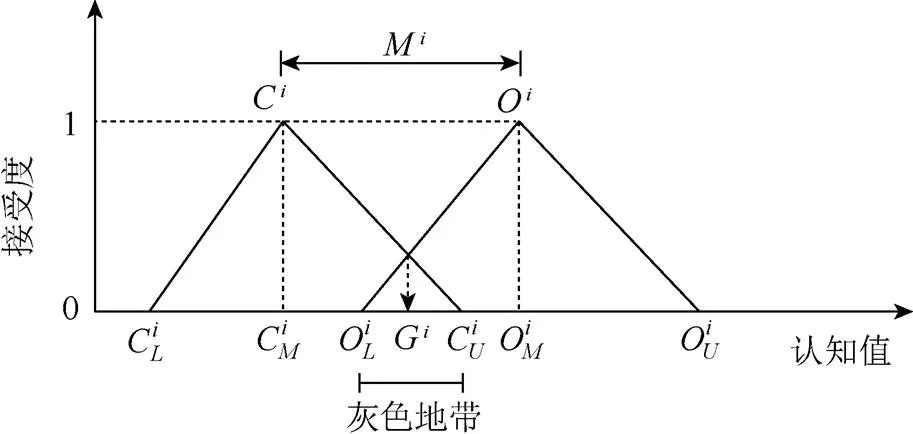
图2 双三角模糊数示意图

1.3 检验行业专家意见共识性

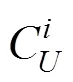
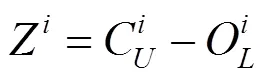
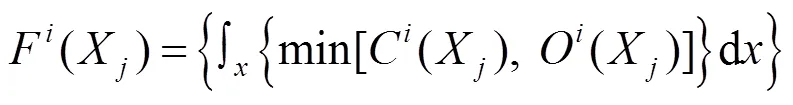
其中，属于评价指标因子。

若Z>M，专家的意见不一致，则重复1.1～1.3节，直至达到收敛。

1.4 计算各评价指标项目的门槛值

一般门槛值由决策者主观确定[20-21]，根据行业专家意见或相关文献设定，也可以通过对所有待筛选的评估指标的G再求一次几何平均数获得。将G与门槛值()进行比较。如果G≥，则选择指标因子；若G＜，则删除指标因子G。对10位行业专家进行问卷调查，按照FDM对有效问卷进行分析与计算。经过两次有效问卷调查后，行业专家意见趋于一致且指标达到收敛状态，测算出每项指标的灰色地检定值，重要性程度共识值。通过再次对G求几何平均数，得出门槛值=7.06。问卷统计分析结果见表1。

根据表1问卷统计分析结果，最终确定的16个二级准则指标为11结构、12材料、13稳定、21功能、22人机、23易用、24便携、31形态、32色彩、33工艺、41教育、42益智、43互动、44趣味、45可持续、46环保，如图3所示。

2 基于FAHP的设计评价模型的构建

FAHP通过系统的数学运算，可以帮助决策者做出更合理地评估。

2.1 构建与检验判断矩阵

以图3所示的儿童滑板车层级指标模型为基础，对10位行业专家进行层次分析问卷调研。10位专家包括儿童滑板车设计专家2人、业务专家2人、产品专家3人及技术专家3人。采用SAATY提出的1～9数值判断尺度表，进行评价指标因素间的对比，并构建判断矩阵。数值代表的重要程度见表2。

将每位行业专家对各层、各个评价指标重要性比较评分的问卷汇总后分别构建判断矩阵。利用Yaahp软件计算所有专家对于各评价指标的权重值，采用几何加权平均处理权重值并求得最终结果。关于指标权重值的确定，首轮有8位行业专家评分构建的矩阵通过了一致性检验，有效问卷的回收比率80%，说明此次问卷设计结构合理。对未通过一致性检验的专家再进行一次问卷评分与统计，直到所有行业专家的意见达到共识，且通过一致性检验。经过了两轮问卷评分，所有行业专家均通过一致性检验。其结果见表3。

表1 问卷统计分析结果

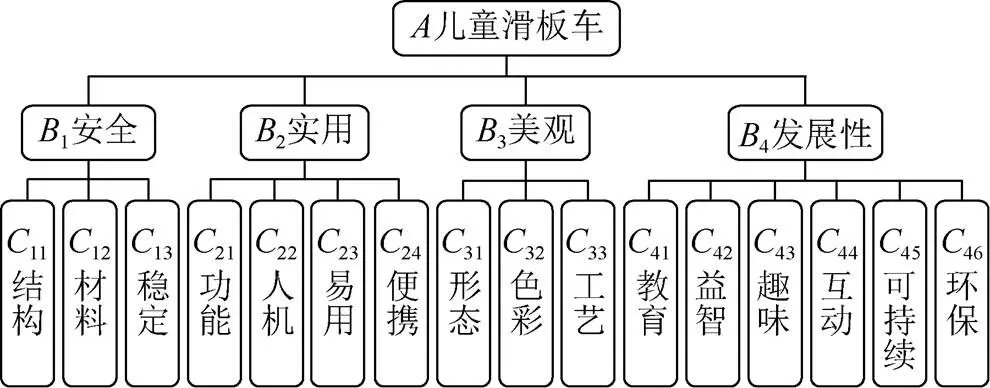
图3 儿童滑板车设计层级指标模型

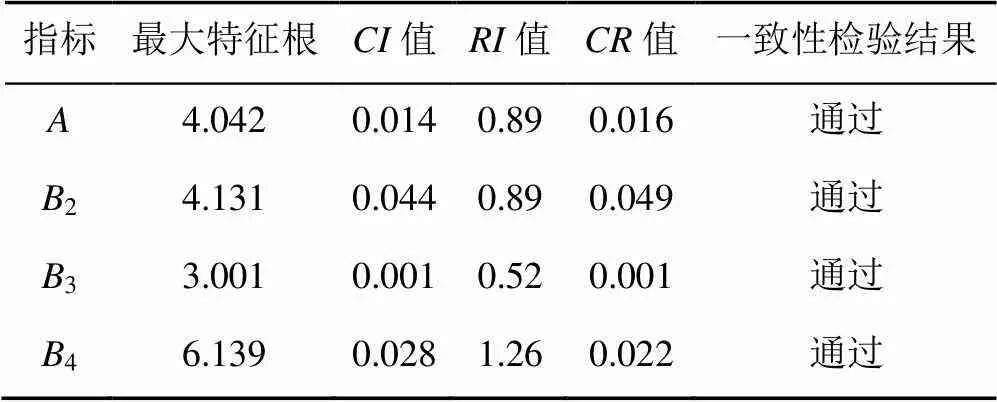
表3 一致性检验结果

2.2 层级指标权重计算

通过一致性检验后，根据判断矩阵中的数值，最终求出指标层层级的权重和绝对权重。绝对权重的大小可直接反映出用户对于儿童滑板车的各个评价因素的喜好程度，同时也能反映评价因素的重要程度。儿童滑板车设计层级指标因素层级权重和各指标综合排序数据见表4。

根据表4中儿童滑板车的各个指标层级的绝对权重，进行综合排序。从综合排序中，可以得出设计相应的侧重点。例如在一级准则指标层1安全(0.426)>2实用(0.299)>3美观(0.102)>4发展(0.173)，因此对于儿童多功能滑板车来说，安全和实用相较于其他2个方面更重要。在二级准则指标层中11结构的绝对权重值为0.184，排名第一，因此结构为最重要的设计评价指标。

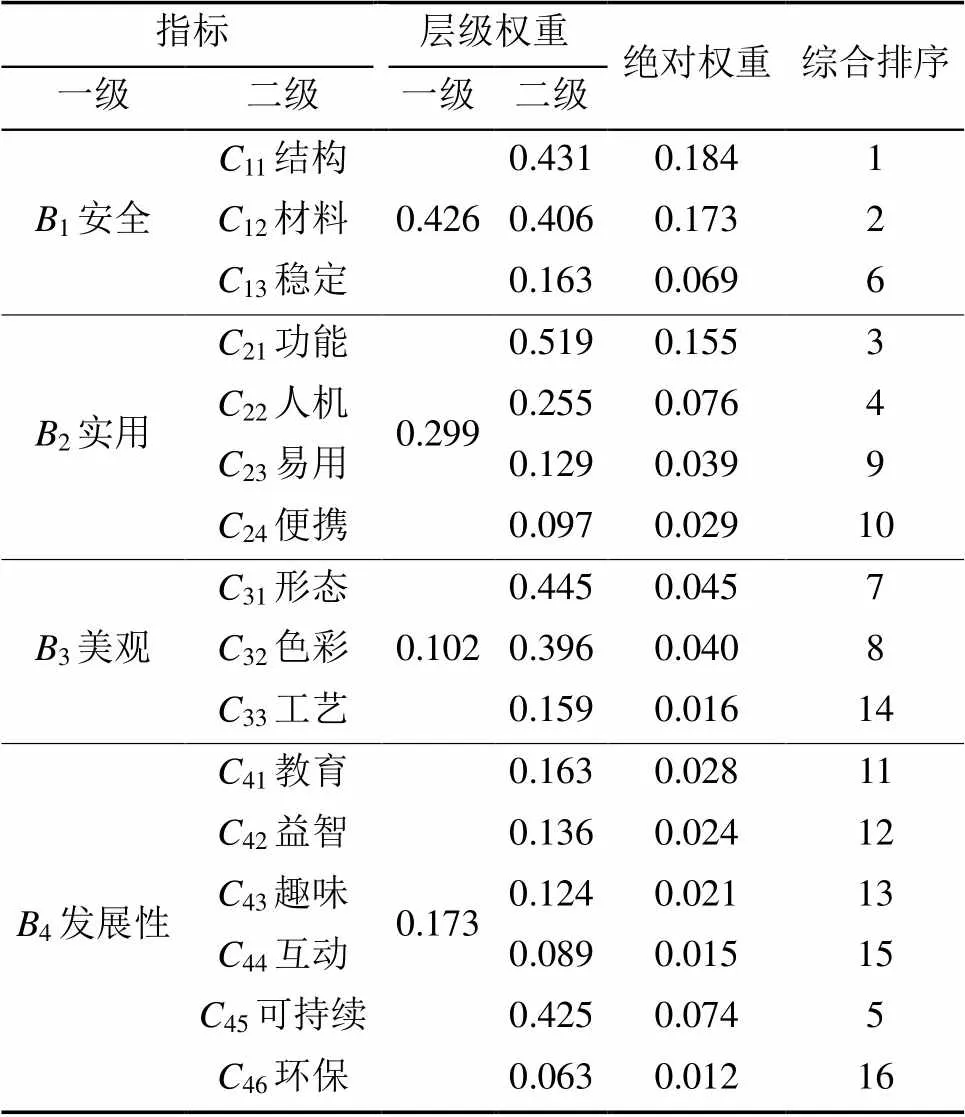
表4 儿童滑板车设计层级指标因素权重数据

2.3 模糊综合评价

设计评价属主观性较强的评价行为，因此可以采用模糊综合评价方法[22]。可利用模糊综合评价方法对多指标要素的评价结果进行量化处理：

(1) 选择行业专家10人对儿童滑板车设计方案进行评价。

(2) 选择评价等级及评价标准。对各个要素采用统一的评语集进行评判，使结果更具有可比性[23]。运用四级法进行等级评价，即={优，良，中，差}。然后为各评价等级赋值，赋值后的评价向量=(90,80,60,50)T，并规定等级标准：90分以上为优，80～89分为良，61～79分为中，60分以下为差。

(3) 确定各层级指标的权重向量。

(4) 根据行业专家的评价结果，构建设计方案的模糊综合评价矩阵。

3 实例应用

3.1 方案设计

通过对儿童滑板车各层级指标评价因素的分析与计算，得出各指标的权重值，由表4可知，一级准则层各评价指标权重值最高的为安全因素(0.426)。由于儿童群体的特殊性，安全是儿童产品设计的第一要素，在设计中要尽可能避免儿童使用过程中的安全隐患。由二级指标层各因素绝对权重值可知，对设计影响较大的因素有结构(0.184)、材料(0.173)、功能(0.155)、人机(0.076)、可持续(0.074)、形态(0.045)和色彩(0.040)在设计中应重点研究。儿童滑板车设计最终效果如图4和5所示。考虑其稳定性在连接与固定方式上采用螺钉与弹性卡扣。使用该产品时可能发生人摔倒和车的损坏意外情况的出现，因此在材料上，使用铝合金车架，在高承重的同时保证安全稳定性，且能快滑不漂。操作杆装有智能传感轴，依靠儿童的身体自然倾斜，以稳定重心，减少意外情况的发生。车头处小鸭子头部和嘴部采用硅胶材质，可以用来按压把玩，增加平衡车的互动性和触感多样性，同时在撞击时也可起到缓冲保护的作用。操作杆通过车把下的按扣结构，可以对其高度尺寸进行三档调节。儿童滑板车具有3种模式功能，用户可以根据儿童的年龄与身高的需求来进行滑板车、平衡车以及三轮车模式，实现滑、骑、坐的自由切换，陪伴儿童健康成长。座位的前部有2个按扣可以固定座位位置和调整座位高度，同时也可以取下座位，易用且便捷。儿童滑板车后轮两边可以打开，由两轮变成三轮模式，适合平衡性较弱的儿童使用。采用仿生造型方法，以儿童喜爱的小鸭子为设计原型，形态可爱有趣。车身整体的颜色以黄色和橙色为主，白色和灰色为辅，色彩明快亲和。

图4 3种功能模式

图5 细节结构图

3.2 综合评价

将得到的模糊综合评价矩阵与AHP得到的层级指标权重进行结合运算。安全下的层级权重为

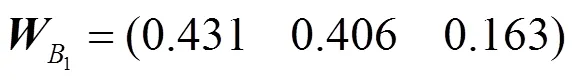
进而得到安全1评价权重向量为

同理得出实用2，美观3，发展4的评价权重向量

将二级准则层的评价权重向量进行组合建立综合矩阵，并用一级准则层的权重与之相乘，得出总评价权重向量

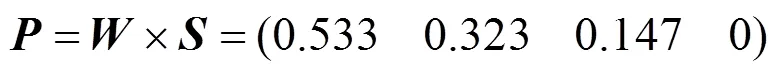
3.3 方案改进意见

将总评价权重向量与评价分值加权计算，最终得到该设计方案的总得分值为82.63。根据模糊评价等级及评价标准，该儿童滑板车设计方案总体上满足用户的需求，达到良的等级，但与优的等级仍有一定的差距。基于表4设计层级指标因素权重数据和实例评价结果表明，对儿童滑板车设计影响较大的因素有结构、材料、功能、人机、可持续、形态、色彩等，从模糊综合评价矩阵依据行业专家对设计方案的模糊综合评价矩阵的打分情况发现，其在稳定、便携、工艺、环保等方面需进一步改进，且目前市场的儿童滑板车多项指标满意度评分偏低。综上，对儿童滑板车提出了产品设计改进策略。

(1) 提高儿童滑板车设计的安全性。由于儿童群体的特殊性，在设计中要尽可能避免儿童使用过程中的安全隐患。儿童滑板车应考虑结构的尺寸合理性和稳定性，使操作舒适便捷，防止夹缝卡住儿童手指等意外情况的发生。材料应是无毒无害的绿色环保材质，特别是材质表面涂料的重金属等化学物质含量也要达标。儿童滑板车是否具有安全的刹车系统，特别在下坡时应防止翻车，急刹时应防止前倾，且发生相撞时也要考虑是否有减震装置结构。因此，安全是儿童滑板车设计的第一指标因素。

(2) 注重儿童滑板车设计的可持续。儿童在生理和心理上都处于快速发展、变化较大的阶段。儿童产品的设计需考虑儿童需求的多样化，也要考虑使用的可持续设计，以免某个年龄段使用后处于闲置状态，造成资源和空间的浪费。从结构的可拆卸与可组合性、功能的可转换与可拓展性、尺寸的可调节性、互动的益智与趣味性，环保的可回收与可重复利用性等方面进行拓展研究，以期满足儿童不断成长的使用需求和社会的可持续性发展。

(3) 加强儿童滑板车设计的情感关怀。儿童6岁之前的教育与引导会对儿童的人格、认知、习惯等有着重要的影响。儿童滑板车作为儿童陪伴产品，需注入更多的情感关怀。儿童滑板车有益于儿童的身心健康发展，互动性情感的设计可也帮助儿童树立自信心，避免孤独感，增加儿童的幸福感。因此在儿童滑板车设计上可以考虑运用仿生形态，采用优美可爱的造型，使人产生亲近感，使产品本身充满情趣和温度。儿童滑板车不仅仅是代步与玩耍的工具，还是陪在儿童身边的朋友和伙伴，也是家人与孩子情感交流的纽带。

4 结束语

针对儿童滑板车设计评价的影响因素复杂多样，各要素与设计方案的关系难以判断等问题，本文提出基于FDM和FAHP的儿童滑板车设计方法。利用FDM定量地评估各项指标的重要性层级，筛选儿童滑板车设计评价指标因素，删除低于门槛值的指标因子，优化层级指标模型，进而保证指标模型的客观性与科学性。通过FAHP能较好地从定性与定量2个层面计算出各项指标权重，综合评价儿童滑板车设计方案，提出改进的设计策略。FDM与FAHP结合可以优化产品设计评价指标体系与设计方案，减少设计过程中的主观因素，让产品设计更加科学、理性与严谨。在模糊层次分析阶段，各个指标要素相对重要性的赋值，有一定的主观不确定性，未来应设计出更科学客观的评判标准。

[1] 胡珊, 刘晶, 王雨晴, 等. 基于用户动态需求的产品迭代创新设计方法研究[J]. 现代制造工程, 2020(12): 41-48.

HU S, LIU J, WANG Y Q, et al. Research on product iterative innovation design method based on user dynamic demand[J]. Modern Manufacturing Engineering, 2020(12): 41-48 (in Chinese).

[2] 杨静. 基于AHP-TRIZ的产品概念创新设计方法研究[J]. 机械设计与制造工程, 2017, 46(7): 97-101.

YANG J. Research on concept innovative design method of product based on AHP-TRIZ[J]. Machine Design and Manufacturing Engineering, 2017, 46(7): 97-101 (in Chinese).

[3] 韩鹏. 面向情感化的儿童滑板车造型设计研究[J]. 机械设计, 2015, 32(11): 123-125.

HAN P. Modeling design of scooter for children facing to emotion[J]. Journal of Machine Design, 2015, 32(11): 123-125 (in Chinese).

[4] BOUZON M, GOVINDAN K, RODRIGUEZ C M T, et al. Identification and analysis of reverse logistics barriers using fuzzy Delphi method and AHP[J]. Resources, Conservation and Recycling, 2016, 108: 182-197.

[5] BOZBURA F T, BESKESE A, KAHRAMAN C. Prioritization of human capital measurement indicators using fuzzy AHP[J]. Expert Systems With Applications, 2007, 32(4): 1100-1112.

[6] LIU Y Y, CHIU Y H. Evaluation of the policy of the creative industry for urban development[J]. Sustainability, 2017, 9(6): 1009.

[7] PHAM T Y, MA H M, YEO G T. Application of fuzzy Delphi TOPSIS to locate logistics centers in Vietnam: the logisticians’ perspective[J]. The Asian Journal of Shipping and Logistics, 2017, 33(4): 211-219.

[8] LEE S, SEO K K. A hybrid multi-criteria decision-making model for a cloud service selection problem using BSC, fuzzy Delphi method and fuzzy AHP[J]. Wireless Personal Communications, 2016, 86(1): 57-75.

[9] WANG W M, PENG H H.A fuzzy multi-criteria evaluationframework for urban sustainable development[J]. Mathematics, 2020, 8(3): 330.

[10] SHAHBOD N, BAYAT M , MANSOURI N, et al. Application of delphi method and fuzzy analytic hierarchy process in modeling environmental performance assessment inurban medical Centers[J]. Environmental Energy and Economic Research, 2020, 4(1): 43-56.

[11] KANG X H, PORTER C S, BOHEMIA E. Using the fuzzy weighted association rule mining approach to develop a customer satisfaction product form[J]. Journal of Intelligent & Fuzzy Systems, 2020, 38(4): 4343-4357.

[12] LIN C. Application of fuzzy Delphi method (FDM) and fuzzy analytic hierarchy process (FAHP) to criteria weights for fashion design scheme evaluation[J]. International Journal of Clothing Science and Technology, 2013, 25(3): 171-183.

[13] 雷磊. 基于FAHP和模糊德尔菲法的产业关键性成功因素评价[J]. 统计与决策, 2014(15): 44-47.

LEI L. Evaluation of the critical success factors of industry based on FAHP and fuzzy Delphi method[J]. Statistics & Decision, 2014(15): 44-47 (in Chinese).

[14] 董文丽, 祝立雄, 李王鸣. 基于模糊德尔菲法的历史文化名城保护规划实施评价研究[J]. 浙江大学学报: 理学版, 2017, 44(6): 749-756.

DONG W L, ZHU L X, LI W M. Research on the assessment of historic city conservation planning implementation based on fuzzy Delphi method[J]. Journal of Zhejiang University: Science Edition, 2017, 44(6): 749-756 (in Chinese).

[15] MURRAY T J, PIPINO L L, VAN GIGCH J P. A pilot study of fuzzy set modification of Delphi[J]. Human Systems Management, 1985, 5(1): 76-80.

[16] ISHIKAWA A, AMAGASA M, SHIGA T, et al. The max-Min Delphi method and fuzzy Delphi method via fuzzy integration[J]. Fuzzy Sets and Systems, 1993, 55(3): 241-253.

[17] LEE A H I, WANG W M, LIN T Y. An evaluation framework for technology transfer of new equipment in high technology industry[J]. Technological Forecasting and Social Change, 2010, 77(1): 135-150.

[18] WANG W M, LEE A H I, CHANG D T. An integrated FDM-ANP evaluation model for sustainable development of housing community[J]. Optimization Letters, 2010, 4(2): 239-257.

[19] 杨拓. 邻避冲突主体间认知差异评估框架与建构方法: 基于模糊德尔菲法的综合运用[J]. 北京航空航天大学学报: 社会科学版, 2015, 28(2): 24-30.

YANG T. Assessment framework and construction methods on NIMBY cognitive differences among the main conflict subjects: based on using fuzzy Delphi method[J]. Journal of Beijing University of Aeronautics and Astronautics: Social Sciences Edition, 2015, 28(2): 24-30 (in Chinese).

[20] DZENG R J, WEN K S. Evaluating project teaming strategies for construction of Taipei 101 using resource-based theory[J]. International Journal of Project Management, 2005, 23(6): 483-491.

[21] WANG W M, LEE A H I, CHANG D T. An integrated FDM-ANP evaluation model for sustainable development of housing community[J]. Optimization Letters, 2010, 4(2): 239-257.

[22] 徐骁琪, 程永胜, 陈国强. 基于AHP法的房车造型评价方法及应用研究[J]. 机械设计, 2020, 37(6): 140-144.

XU X Q, CHENG Y S, CHEN G Q. Evaluation method and application of RV modeling based on AHP method[J]. Journal of Machine Design, 2020, 37(6): 140-144 (in Chinese).

[23] 贾驰千, 冯冬芹. 基于模糊层次分析法的工控系统安全评估[J]. 浙江大学学报: 工学版, 2016, 50(4): 759-765.

JIA C Q, FENG D Q. Security assessment for industrial control systems based on fuzzy analytic hierarchy process[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(4): 759-765 (in Chinese).

Design evaluation and improvement of Children’s scooter based on FDM and FAHP

WANG Zhi-yuan1,2, DAI Zhi-peng3

(1. School of Mechanical Engineering, Anhui University of Science and Technology, Huainan Anhui 232001, China; 2. State key laboratory of Mining Response and Disaster Prevention and Control in Deep Coal Mines, Anhui University of Science and Technology, Huainan Anhui 232001, China; 3. School of Chemical Engineering, Anhui University of Science and Technology, Huainan Anhui 232001, China)

The influencing factors of the design evaluation of children’s scooter are complex and diverse, and it is difficult to measure the importance of these factors to product design through quantitative methods. Fuzzy Delphi method (FDM) was employed to quantitatively screen product design evaluation index elements, and a hierarchical index model for design of children’s scooter was established. Then, the fuzzy analytic hierarchy process (FAHP) was adopted to calculate the weight of each indicator element, the design plan was comprehensively evaluated, and the overall evaluation score of children’s scooter was obtained. Finally, the suggestions for optimization and improvement were proposed. The combination of FDM and FAHP can systematically design and evaluate products quantitatively, reduce non-objective factors in the design process, make the design more scientific, rational and rigorous, which also provides a quantifiable reference basis for the selection and optimization of children’s product design schemes.

industrial design; children’s scooter; fuzzy Delphi method; fuzzy analytic hierarchy process; design evaluation index

TB 472

10.11996/JG.j.2095-302X.2021050849

A

2095-302X(2021)05-0849-07

2021-01-28；

2021-03-17

28 January，2021；

17 March，2021

安徽省质量工程资助项目(2019jyxm1150)

Anhui Quality Engineering Funding Project (2019jyxm1150)

王志愿(1986–)，女，安徽淮北人，讲师，硕士。主要研究方向为工业设计。E-mail：xinyuan8610@126.com

WANG Zhi-yuan (1986–), female, lecture, master. Hermain research interest covers industrial design. E-mail：xinyuan8610@126.com