车辆-抬轮器耦合动力学性能分析
杨鸿泰,黄志辉,郑志伟,张伟忠
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031;2. 河北通海瑞宏铁路机具有限公司,河北 石家庄 050000)
车辆运行过程中因轴承烧损、齿轮卡死等情况导致轮对卡死,从而造成线路瘫痪,严重影响铁路运输秩序。目前主要的救援方法是车载法,即将抬轮器放置在故障轮对下面,支撑轮对并代替轮对运行。车载法通用性强,使用方便,但使用过程中选取抬轮器运行速度往往凭借经验,缺乏相应的理论参考,导致救援效率低下,甚至可能发生二次事故。本文将通过建立车辆-抬轮器耦合模型,对其动力学性能进行分析,以期为今后救援时选取抬轮器运行速度提供理论参考。
1 车辆-抬轮器耦合动力学模型
抬轮器由抬轮器车轮、抬轮轴和连接板组成。抬轮器安装在故障轮对下面,前后抬轮轴用来固定和支撑故障轮对,代替故障轮对运行。抬轮器在故障轮对下的安装方式如图1所示。

图1 抬轮器在故障轮对下的安装方式
运用多体动力学仿真软件SIMPACK建立车辆-抬轮器耦合动力学模型,对车辆和抬轮器组成的多体系统进行分析计算。抬轮器动力学模型包括2条抬轮器轮对、前后抬轮器轮对之间的连接板。连接板与前后抬轮器轮对耦合在一起,如图2所示。而车辆动力学模型中,将车辆轮对分别建立在抬轮器连接板上,通过约束与连接板耦合,二者形成一个整体。依次建立构架、轴箱、车体等刚体,形成整个车辆-抬轮器耦合动力学模型,模型中包括1辆车体、2个构架、4条车辆轮对、8个轴箱、8条连接板、8条抬轮器轮对,如图3所示。抬轮器轮轨接触几何关系见图4,车辆动力学主要计算参数见表1,整车自由度情况见表2。

图2 抬轮器动力学模型

图3 车辆-抬轮器耦合动力学模型
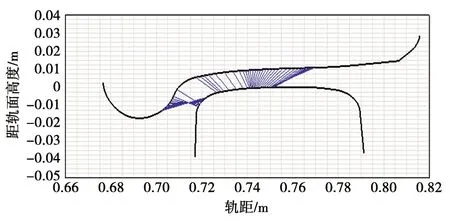
图4 抬轮器轮轨接触几何关系图
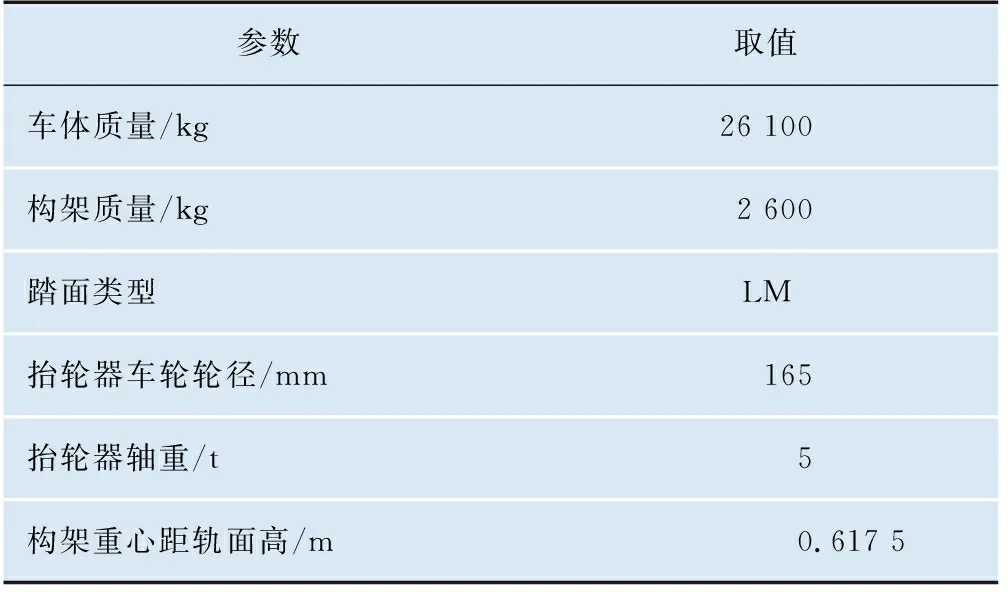
表1 车辆动力学主要计算参数

表2 整车自由度
2 车辆-抬轮器运动稳定性分析
2.1 非线性临界速度计算方法1
轨道激励分别采用美国Ⅳ级谱和美国Ⅴ级谱,让耦合模型通过不平顺轨道并激发其振动,然后再在理想光滑轨道上运行,通过观察抬轮器轮对的横向振动是否衰减到平衡位置,从而判断耦合模型是否发生蛇行失稳。
通过计算,以抬轮器轮对为研究对象,车辆-抬轮器耦合模型在美国Ⅳ级轨道谱、Ⅴ级轨道谱下的蛇行失稳临界速度分别为225 km/h、288 km/h。满足运行要求并具有足够的安全裕量。
2.2 非线性临界速度计算方法2
利用文献[1]中介绍的UIC 515法研究车辆-抬轮器耦合模型的运动稳定性。考虑到车辆-抬轮器耦合模型中车辆轮对与抬轮器连接板耦合在一起,故横向振动加速度采样点选在抬轮器连接板上[1],研究抬轮器运行速度为5~50 km/h时的动力学性能。
计算结果如图5所示,当抬轮器运行速度小于40 km/h时,以抬轮器连接板为研究对象,抬轮器稳定性符合要求;当抬轮器运行速度大于40 km/h时,则存在一定的安全风险。
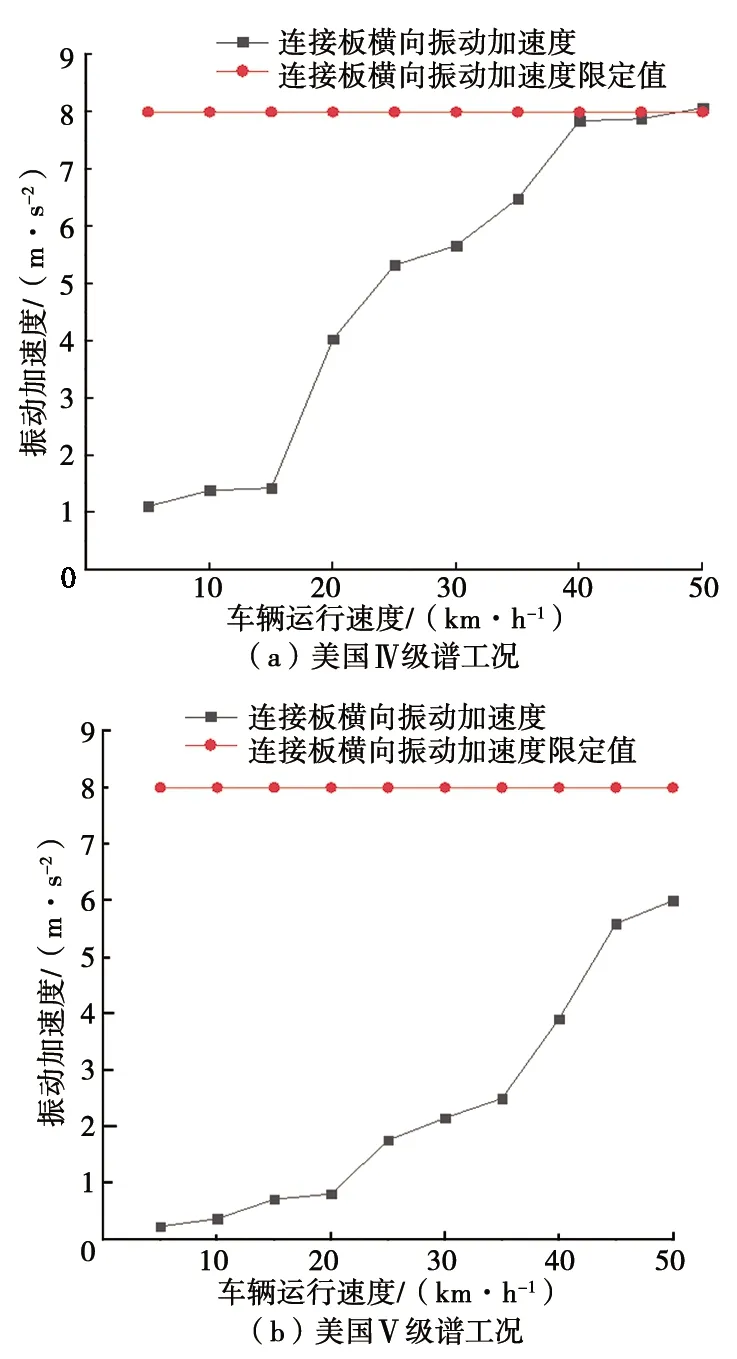
图5 连接板横向振动加速度随速度变化图
3 车辆-抬轮器运行平稳性分析
轨道激励采用美国Ⅳ级谱,按GB/T 17426—1998《铁道特种车辆和轨行机械动力学性能评定及试验方法》的规定[2],车辆抬轮器耦合模型在5~50 km/h速度范围内运行,计算结果见图6和图7。结果表明:在美国Ⅳ级谱激扰下,横向、垂向平稳性指标分别为2.42、2.58,均为“优”级;横向、垂向振动加速度最大值分别为1.185 m/s2、0.943 m/s2,均远低于限定值。
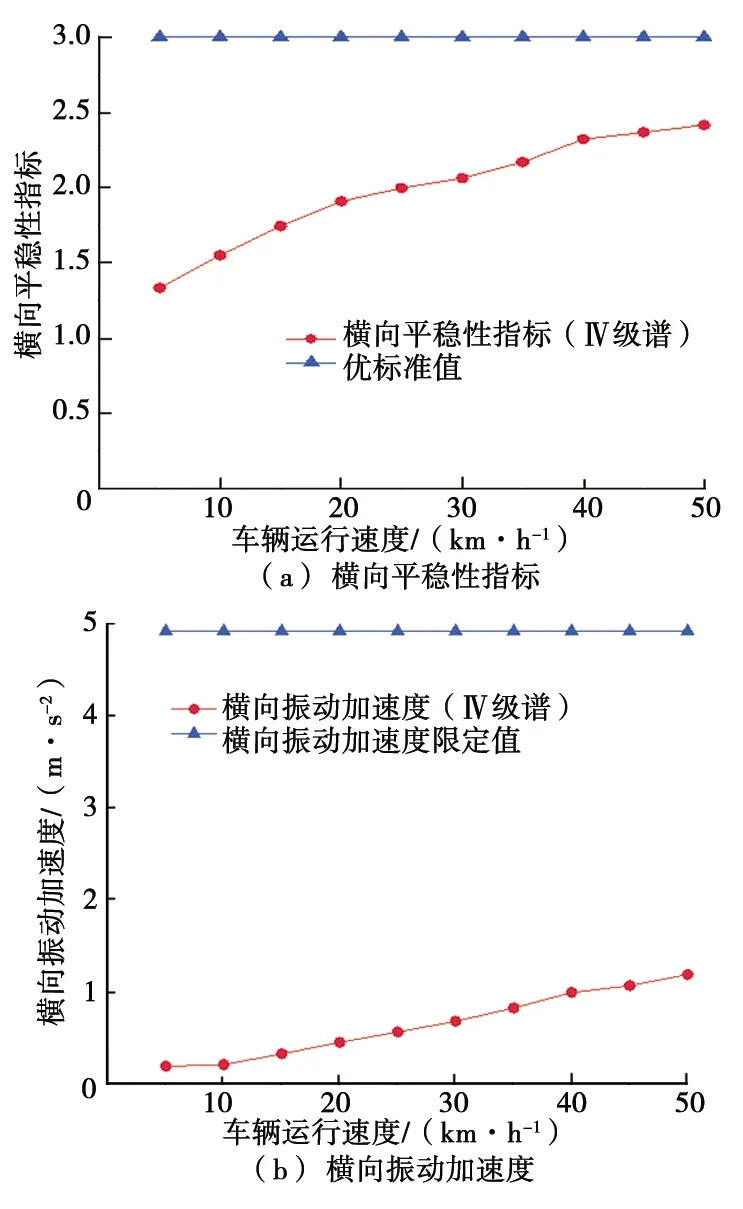
图6 整车横向平稳性评价指标随速度变化图

图7 整车垂向平稳性评价指标随速度变化图
4 车辆-抬轮器曲线通过性能分析
曲线轨道参数设置如下:直线段30 m,缓和曲线长度70 m,圆曲线长度60 m,曲线半径选取600 m、800 m、1 000 m 3种工况,轨道激励采用美国Ⅳ级谱,车辆-抬轮器运行速度为5~50 km/h。计算结果见图8~图10。从图8~图10中可以看出,轮轴横向力最大值为27.4 kN,小于限定值33.8 kN;脱轨系数最大值为0.64,小于限定值1.0;轮重减载率最大值为0.28,小于限定值0.6。
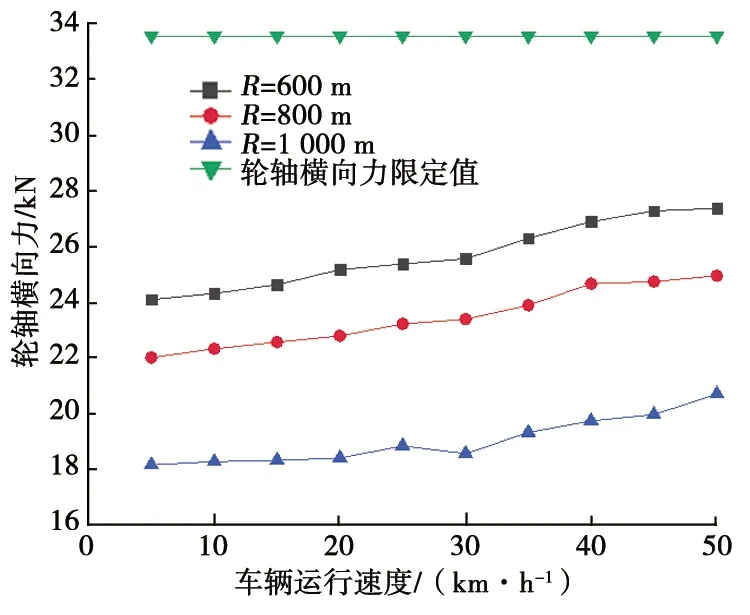
图8 轮轴横向力
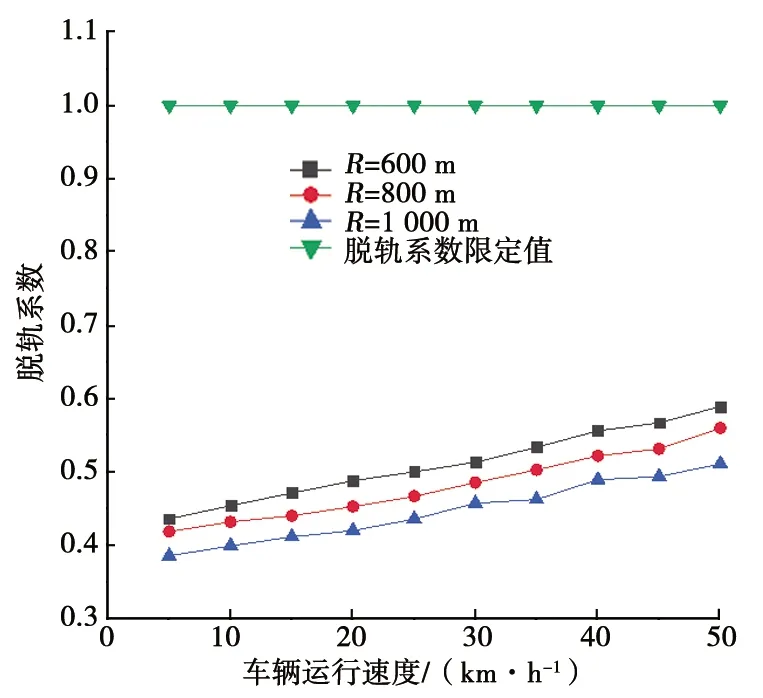
图9 脱轨系数
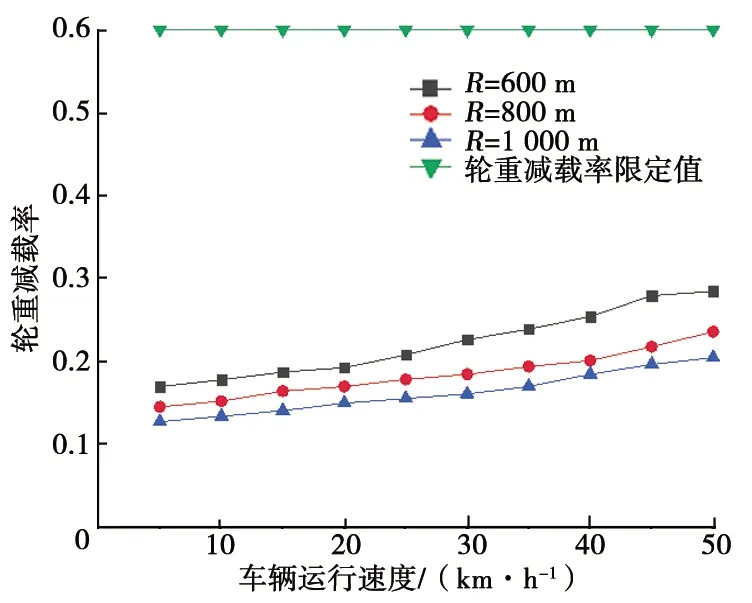
图10 轮重减载率
5 结论
(1) 轨道激励分别采用美国Ⅳ级谱和美国Ⅴ级谱,车辆-抬轮器耦合模型以抬轮器轮对为研究对象时,非线性临界速度分别为225 km/h和288 km/h,相比于实际运行速度为5~15 km/h,安全裕量非常大。
(2) 在美国Ⅳ级谱激扰下,车辆-抬轮器耦合模型在5~50 km/h运行速度范围内,横向、垂向平稳性指标均为“优”级,横向、垂向振动加速度最大值均远低于限定值。
(3) 在文中假设的曲线运行工况下,车辆-抬轮器具有良好的曲线通过性能。
(4) 车辆-抬轮器的运行速度可由当前的5~15 km/h提高至5~35 km/h,进而提高救援效率。今后将重点研究车辆-抬轮器的道岔通过性能。

