灌区小型梯形渠道圆直形量水槽试验

戚玉彬 张月云 贺光华 王昆

摘 要：为了缓解灌区小型梯形渠道量水设施短缺的问题，设计了一种简易的圆直形量水槽。通过π定理推导量水槽流量的函数关系式，在3条梯形渠道上选用5种收缩比进行现场试验，分析了圆直形量水槽的量水性能指标。结果表明：基于π定理和灌区现场试验得到的流量公式平均相对误差为2.32%;对于坡度大于1/300的梯形渠道，量水槽收缩比小于0.5时，槽前弗劳德数可以满足测流要求;量水槽壅水高度在18.8 cm以下，不影响渠道的正常运行;圆直形量水槽可以在灌区小型梯形渠道上进行测流。

关键词：小型梯形渠道;圆直形量水槽;量水试验

中图分类号：S274.4 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.10.030

引用格式：戚玉彬，张月云，贺光华，等.灌区小型梯形渠道圆直形量水槽试验[J].人民黄河，2021，43（10）：154-156，160.

Abstract： In order to alleviate the shortage of water measuring facilities for small trapezoidal channels in irrigation areas， a simple circular straight measuring flume was designed. Based on the π theorem， the functional relationship of the discharge formula of measuring flume was deduced. Five types of contraction ratios were used in three small trapezoidal channels for field test in irrigation areas. The water measurement performance index of circular straight measuring flume was analyzed. The results show that the average relative error of flow formula based on π theorem and field test in irrigation area is 2.32%. For trapezoidal channels with a slope greater than 1/300， Froude number in front of measuring flume can meet the requirement of flow measurement when the contraction ratio of measuring flume is less than 0.5. The backwater height of the measuring flume is below 18.8 cm， which can not affect the normal operation of the channel. The circular straight measuring flume can be used to measure flow in small trapezoidal channels of irrigation area.

Key words： small trapezoidal channel; circular straight measuring flume; test of water measurement

灌區量水是准确调整农业用水、实施灌溉计划和管理用水的必要措施，也是灌区管理的一项关键技术[1-2]。梯形渠道水力性能优良，易施工和管理，目前仍是灌区广泛应用的末级渠道形式[3]。国内外学者提出的梯形渠道量水设施主要有圆柱形[4-7]、弧形[8]、机翼形[9]、梯形喉口[10-12]等量水槽，大多以模型试验或数值模拟的形式进行研究，并未在灌区开展现场试验、检验量水效果。目前灌区梯形渠道应用较多的量水设施仍然是巴歇尔槽和梯形堰。巴歇尔量水槽常用于干、支渠的梯形渠道量水，其结构复杂，在末级渠系的小型梯形渠道上很难精确修筑。梯形量水堰常用于灌区末级渠系梯形渠道量水，但其堰高高于渠底，堰前极易沉积杂物而使量水精度降低，并且梯形量水堰使用时，需要另外修建一段梯形渠道与之配套，增加了施工工序和造价。针对灌区末级渠系中小型梯形渠道的量水现状，笔者设计了一种可直接建造在小型梯形渠道上的简易圆直形量水槽，并在灌区开展现场试验，分析研究圆直形量水槽的量水性能指标，检验其在灌区小型梯形渠道实际应用的可行性，以期为灌区小型梯形渠道提供一种简易实用的量水设备。

1 试验情况

1.1 圆直形量水槽

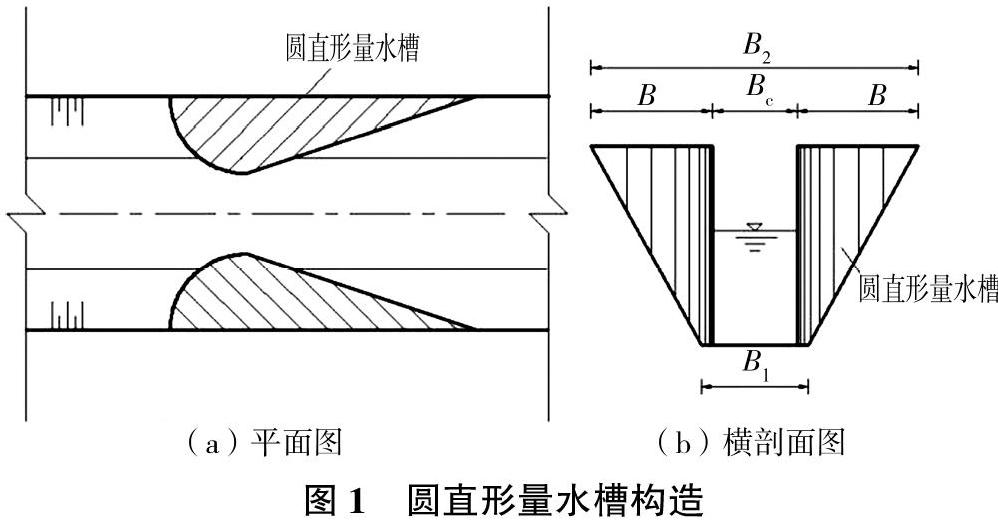
圆直形量水槽设计为无喉量水槽，由1/4圆曲线形式的收缩段和直线形式的扩散段组成。量水槽采用预制的钢模板，直接建造在梯形渠道内，不需要破除原有渠道，施工简单。收缩段的圆曲线控制方程为

x2+y2= B2（1）

式中：B=（B2-Bc）/2，其中B2为渠上口宽、Bc为喉口宽。

圆直形量水槽的构造形式见图1，B1为渠底宽。

1.2 试验情况

试验地点为某灌区的3条小型梯形渠道。梯形渠道通过分水闸直接连接在干渠上，分水闸起到调配水的作用。分水闸后建有一段匹配梯形量水堰的过渡段渠道。梯形量水堰按《灌溉渠道系统量水规范》的标准尺寸制造，并定期进行校准。梯形量水堰的堰口下底宽0.5 m，水尺精度为0.001 m。为保证试验水流的稳定性，圆直形量水槽位于梯形量水堰之后的一段距离。在圆直形量水槽前1 m和槽后5 m处，分别设置上游、下游水尺，用于观测圆直形量水槽的上游、下游水深。水尺用测量仪器准确标记在梯形渠道内壁上，上游、下游水尺精度均为0.001 m。

1.3 圆直形量水槽试验设计

设计圆直形量水槽时，依据渠道比降先初选收缩比。由于当地灌区位于山前冲积扇平原，地面坡度较大，梯形渠道的比降以1/300～1/100之间居多，本试验中选取的梯形渠道比降均大于1/300。

将圆直形量水槽喉口断面面积与梯形渠道断面面积的比值作为量水槽的收缩比。为使量水槽既能形成临界水流，又能最大程度减少上游壅水，并参考收缩比的适宜选择范围[6]，本试验共选择5种收缩比。

收缩比选定后，根据收缩比计算得到喉口宽度和量水槽宽度。为便于运输和减少工程量，量水槽槽长设计为量水槽宽度的4～5倍。圆直形量水槽和梯形渠道试验设计见表1。

2 流量公式

2.1 理论推导

圆直形量水槽的流量公式可用π定理来推导。设梯形渠道流量为Q，量水槽槽前水深为h，量水槽喉口宽度为Bc，梯形渠道上口宽度为B2，重力加速度为g，动力黏滞系数为μ，根据量纲分析可写出如下的函数式：

综上，利用π定理推导得到圆直形量水槽流量的隐函数关系式。通过田间现场试验，可进一步确定圆直形量水槽的流量公式。

2.2 流量公式

灌区现场试验共计得到数据429组，代入式（13），结果见图2。相对水深h/Bc与相对流量Q/（B2.5c·g0.5）相关关系良好，R2=0.993。通过进一步拟合分析，幂函数的指数为1.376，系数为0.742，最终得到梯形渠道圆直形量水槽流量公式为

根据试验条件，式（14）适用于糙率系数为0.017、流量为0.08～0.19 m3/s、比降大于1/300的小型梯形渠道。

3 量水性能指标分析

3.1 量水精度分析

将式（14）计算结果作为计算流量，与梯形量水堰的实测流量进行对比，见表2。式（14）所得的计算流量平均相对误差仅为2.32%。因此，通过π定理和灌区现场试验得到的圆直形量水槽流量公式可以满足灌区量水精度要求。

3.2 槽前弗劳德数分析

要保证测流的准确性，就必须控制槽前弗劳德数的大小，量水规范要求槽前弗劳德数小于0.5[13]。图3为圆直形量水槽各收缩比在不同流量时弗劳德数的变化情况。由图3可知，弗劳德数受量水槽收缩比的影响大，流量不变时，收缩比越大弗劳德数也越大。在本试验中弗劳德数的变化范围是0.41～0.66，当梯形渠道比降大于1/300、收缩比小于0.5时，可以满足量水规范中对弗劳德数的要求。

3.3 槽前壅水高度分析

实际应用中，量水槽相当于阻水建筑物，在量水槽前段产生壅水，导致槽前水位壅高[14]。渠道上游水深与下游水深之差即为壅水高度。由图4可知，流量变大时，壅水高度也随之变大。收缩比增大时，壅水高度却在减小。本试验中，收缩比为0.49～0.67时，壅水高度均小于18.8 cm，未出现槽前渠水溢出。

4 结 语

基于π定理和灌区现场试验得到的圆直形量水槽流量公式，可以满足灌区小型梯形渠道的量水精度要求。弗劳德数受收缩比影响大，对于比降大于1/300的梯形渠道，收缩比小于0.5时，弗劳德数可以满足测流要求。在收缩比为0.49～0.67的范围内，圆直形量水槽的壅水高度均小于18.8 cm，不影响渠道的正常运行。因此，圆直形量水槽可以在灌区小型梯形渠道上进行测流。

参考文献：

[1] 孙西欢，马娟娟，周义仁.灌区量水技术及其自动化[M].北京：中国水利水电出版社，2014：1-11.

[2] 栗克国，孟祥杰，李志飞，等.一种轨道式渠道自动测流系统的研制与应用[J].人民黄河，2018，40（7）：150-156.

[3] 吕宏兴，裴国霞，杨玲霞.水力学[M].北京：中国农业出版社，2011：237-238.

[4] 蔡勇，李同春，吉庆丰，等.梯形渠道圆柱形量水槽的试验研究[J].中国农村水利水电，2005（8）：63-66.

[5] 吉慶丰，袁晓渊，葛蕴，等.梯形渠道圆柱形量水槽水力特性数值模拟[J].灌溉排水学报，2012，31（2）：59-61.

[6] 刘嘉美，王文娥，胡笑涛，等.梯形渠道圆柱形（带尾翼）量水槽试验研究[J].灌溉排水学报，2013，32（6）：23-26.

[7] DAVIS S. Simple Flow Measurement Devices for Open Channels[R]. Las Cruces： New Mexico State University，2016：6-30.

[8] 于国丰，赵凤伟，姜英震，等.梯形渠道移动式弧形量水槽的试验研究[C]//中国水利学会.中国水利学会2008学术年会论文集（上册）.北京：中国水利水电出版社，2008：177-180.

[9] 潘志宝，吕宏兴，张晓斐，等.梯形渠道机翼形量水槽试验[J].农业机械学报，2009，40（12）：97-100.

[10] 冉聃颉，王文娥，胡笑涛，等.梯形喉口无喉道量水槽水力性能分析[J].水科学进展，2018，29（2）：236-244.

[11] 冉聃颉，王文娥，胡笑涛.梯形喉口无喉道量水槽设计及其水力性能模拟与试验[J].农业工程学报，2017，33（15）：177-183.

[12] RAN Danjie， WANG Wene， HU Xiaotao. Three-Dimensional Numerical Simulation of Flow in Trap Ezoidal Cutthroat Flumes Based on FLOW-3D[J]. Frontiers of Agricultural Science and Engineering， 2018， 5（2）： 168-176.

[13] 中华人民共和国水利部.灌溉渠道系统量水规范：GB/T 21303—2017 [S].北京：中国标准出版社，2008：26-34.

[14] 美国内政部垦务局.量水手册[M].北京：中国水利水电出版社，2011：127-128.

【责任编辑 许立新】