基于改进非负矩阵分解算法的人脸识别研究

王焕庭，王鑫印

(1.桐城师范高等专科学校，安徽 桐城 231400；2.上海电力大学，上海 200333)

信息化时代背景下数据呈现出高维、海量的特点，对各种数据的处理往往借助于计算机来实现。各种数据在计算机的存储是以矩阵的形式，如图像的像素数据和矩阵相对应。处理高维、海量数据的关键是降维，通过矩阵分解将规模比较大的复杂问题转变为规模比较小的简单问题。传统的矩阵分解算法有主成分分析法、独立分量分析法、奇异值分解算法等，这些方法的缺点是不能确保矩阵分解结果的非负性。尽管从数学的角度来讲，分解的结果中出现负值是正常的，但是负值在实际问题中往往无意义、无法解释。非负矩阵分解(NMF)由Lee和Seung在1999年提出，其有效解决了传统矩阵分解中存在的负数问题[1]。NMF是一种新的矩阵分解算法，对矩阵的元素加入了非负性的约束，使得分解得到的矩阵元素不存在负值，这样在实际应用中就会具有明确的物理意义。另外，NMF分解所得到的矩阵具有一定程度的稀疏性，这样能够达到抑制外界噪声干扰的目的[2]。目前，非负矩阵分解被广泛应用于机器学习、模式识别等领域中，具有重要的理论意义和应用价值。

1 非负矩阵分解

1.1 非负矩阵分解定义

非负矩阵分解是一种多变量分解的方法，对非负矩阵An×m进行线性分解，

An×m≈Un×rVr×m

(1)

其中，矩阵U为基矩阵，矩阵V为稀疏矩阵。

采用稀疏矩阵V替代矩阵A，那么就实现了对原矩阵A的降维处理，通过非负矩阵分解达到了减少存储空间，节约计算资源的目的[3]。

1.2 非负矩阵分解算法

标准非负矩阵分解是一个优化问题，通过定义目标函数来度量分解的程度与迭代的规则。Lee和Seung定义了矩阵A与UV的F-范数以及K-L散度两个目标函数[4]。矩阵A和UV之间的F-范数如式(2)所示，矩阵A和UV之间的K-L散度如式(3)所示。

(2)

+(UV)ij)

(3)

对于式(2)和式(3)这两个目标函数，单独考虑U或者单独考虑V，其均为凸函数，但是如果同时考虑U和V，那么这两个目标函数就不再是凸函数。因此，找到两个目标函数的最优解是不现实的，只有去寻找局部最优解才是可行的。

按照公式(4)和(5)进行迭代运算，

(4)

(5)

按照公式(6)和(7)进行迭代运算，

(6)

(7)

此时，目标函数D(A‖UV)单调非增。

进行非负矩阵分解的关键在于获得有效的迭代公式，不论是基于F-范数还是基于K-L散度，其非负矩阵分解的流程类似，具体如图1所示。

图1 非负矩阵分解流程

令基矩阵U和稀疏矩阵V第n次迭代结果为Un和Vn，第n+1迭代结果为Un+1和Vn+1。非负矩阵分解算法收敛的条件是对于任意ε1>0和ε2>0，均满足D(Un+1‖Un)<ε1和D(Vn+1‖Vn)<ε2。ε1和ε2为收敛精度，D为K-L散度。该种进行非负矩阵分解的算法称之为乘性迭代算法。由于该种算法综合考虑了算法的效率和实现的难易程度，同时在实际应用中效果也比较好，因此常常被作为经典的算法进行引用和介绍。

1.3 非负矩阵分解算法改进

对于乘性迭代算法而言，其收敛速度相对比较慢，同时也存在不稳定，因此需要对其进行改进。改进非负矩阵分解算法的思想是仅仅保留非负约束条件，最速下降法是求解无约束问题的有效方法，因此采用最速下降法求解，同时通过添加稀疏约束条件来提高算法的计算效率，从而得到改进后的非负矩阵分解算法(SNMF)[5]。

设函数f连续可微，负梯度方向dk为函数f数值下降最快的方向，即

dk=-▽f(xk)

(8)

令步长为λk，那么第k+1次迭代为

xk+1=xk+λkdk=xk-λk▽f(xk)

(9)

能够通过少量元素近似替代大量数据称之为稀疏，通常利用向量1范数和向量2范数来对稀疏度进行衡量，定义式为

(10)

式中：n为向量x的维数，‖·‖1为1范数，‖·‖2为2范数。

假设矩阵V已知，同时要求矩阵U的所有元素之和为1，使得‖U‖2最大化，此时可以使得矩阵U的稀疏度比较大。设目标函数为

(11)

将负梯度方向设置为下降的方向，设φia为负梯度方向步长，那么

(12)

由于

(13)

因此令步长φia为

(14)

关于矩阵U的迭代公式为

(15)

假设矩阵U已知，同时要求矩阵V的所有元素之和为1，使得‖V‖1最小化，此时可以使得矩阵V的稀疏度比较大。设目标函数为

(16)

将负梯度方向设置为下降的方向，设μai为负梯度方向步长，那么

(17)

关于矩阵V的迭代公式为

(18)

改进非负矩阵分解算法的流程为：

1)设置分解误差，初始化非负矩阵Uia>0和Vaj>0；

2)运用矩阵U和矩阵U的迭代公式进行迭代运算；

3)判断‖A-UV‖误差是否小于设置的分解误差ε以及迭代次数是否达到最大值，得到分解结果。

2 非负矩阵分解在人脸识别中的应用

2.1 智能识别应用概述

非负矩阵分解的算法实现简便、有效，被广泛应用于模式识别研究领域的特征提取和数据降维中，在高维、海量数据的处理中具有十分广泛的应用前景。

2.1.1 图像识别

图像是以矩阵的形式存储在计算机中，这使得非负矩阵分解在进行图像分析和识别中大有用武之地。对图像矩阵进行非负矩阵分解，有效提取图像的本质特征，找出图像内部的关系，同时将提取的特征用于图像识别、图像降噪、图像融合中[6]。目前应用比较广泛的有利用非负矩阵分解进行人脸检测、图像融合、图像复原、图像压缩等等。

2.1.2 文本聚类

一般的文本数据信息量巨大且无固定结构，但典型文本数据通常采用矩阵形式在计算中存储并处理[7]。计算机所存储的文本数据矩阵具有高维、稀疏的特点，因此海量的文本信息处理必须降低原始数据的维数。非负矩阵分解算法可以有效地捕捉文本中的语义和相关信息，实现对文本的聚类分析[8]。商业数据库软件Oracle采用非负矩阵分解算法对文本的特征进行提取，同时在特征提取的基础上进行分类。

2.1.3 语音识别

语音在国民生活中随处可见，同时语音数据包含有巨大的信息量，这使得对语音的识别具有至关重要的现实意义。采用非负矩阵分解可以有效地提取语音信息特征，通过语音信息特征的提取以借助于机器实现语音的自动识别[9]。如对复调音乐信号矩阵进行非负矩阵分解来实现对不同调子的识别，并记录不同的音调。

2.1.4 机器人控制

工业生产中机器人的应用越来越广泛，对物体的高效、准确识别是机器人研发的核心技术。机器人只有快速、准确地识别周围的物体，才能更好地开展工作，使得机器人的智能化程度提高。借助外设获取周围环境数据，环境数据以矩阵的形式存储在计算机中，采用非负矩阵分解算法来使得机器人完成对特定目标的识别。

2.2 人脸识别应用实例

人脸识别是模式识别的一个重要方向，本部分针对非负矩阵分解在人脸识别中的应用进行研究。人脸识别是利用计算机来提取人脸的相关特征从而达到对人身份进行辨别的目的。图2给出了人脸识别的流程[10]。

图2 人脸识别流程

2.2.1 试验数据来源

试验数据来源于ORL人脸数据库。ORL人脸数据库共包含有40个人的人脸信息，包括其在不同的光照条件下、不同的表情下、不同的面部饰物下、不同的姿态下所拍摄的照片。所拍摄的每一张照片像素大小为112×92。ORL人脸数据库中共包含有400张灰度图像，对40个人每个人选择5张作为训练集，共有200张图片作为训练集，剩下的200张图片作为测试集。

2.2.2 试验过程描述

训练集中包含有200个训练样本，将每一个样本像素矩阵的每一列元素串成一列，使得每一个样本用一个列向量表示，那么整个训练样本矩阵为A10304×200。对训练样本矩阵A进行非负矩阵分解，得到基矩阵U和稀疏矩阵V。最后求解得到重构图像A=UV。

2.2.3 试验结果分析

设定误差ε=0.05，λ1=0.02，λ2=0.01，分别进行300次和500次迭代，降维维度r为30和50，对比NMF算法和SNMF算法的结果。图3为迭代次数为300次，降维维度r=30的重构后图像。图4为迭代次数为500，降维维度r=50的重构后图像。

通过对比图3和图4可知，随着迭代次数的增加和降维维度的增加，所重构出的图像变得越来越清晰。由表1可见，迭代的次数增加和降维维度的增加使得算法的运行时间变长，但是不论是迭代次数300次还是500次，降维维度是30还是50，采用SNMF算法的运行时间均小于NMF算法，即改进的非负矩阵分解算法效率有一定程度的提升。

图3 迭代300次降维维度30的重构后图像

图4 迭代500次降维维度50的重构后图像

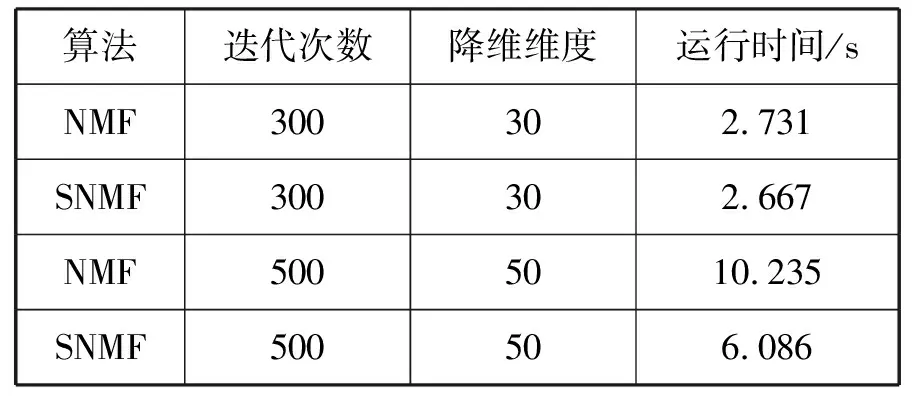
表1 运行时间对比

3 结论

非负矩阵分解具有明确的物理意义和良好的可解释性，这使得其在机器学习、模式识别等领域得到了广泛的应用。在对非负矩阵分解算法进行研究的基础上，给出了其在模式识别中的应用。对于非负矩阵分解算法而言，其将高维的数据映射到低维的空间，获取原数据的本质信息。采用最速下降法且添加稀疏约束条件对非负矩阵分解进行改进，并应用于人脸识别中，通过和传统非负矩阵分解算法进行对比，显示改进的非负矩阵分解算法在人脸识别中的效率大大提升，这对人脸识别的研究具有一定的理论参考价值。