一种基于PILCO算法的智能浮体运动控制方法

张 尚, 杨 睿,2, 陈 震,2, 黎 明,2

一种基于PILCO算法的智能浮体运动控制方法

张 尚1, 杨 睿1,2, 陈 震1,2, 黎 明1,2

(1.中国海洋大学 工程学院, 山东 青岛, 266100; 2.山东省海洋智能装备技术工程研究中心, 山东 青岛, 266100)

随着人们对海洋探索的不断深入, 开发一种自主性强、灵活度高、可重构的智能浮体(ASV)至关重要。文中以四推进器ASV为研究对象, 建立了其动力学模型, 基于概率推理的学习控制算法设计了控制器, 并进行了定点控制和轨迹跟踪的仿真实验。仿真结果表明: ASV仅需进行少量的实验即可获得自主学习控制策略, 在有水流扰动或采用近似动力学模型时, 能够实现对其的运动控制, 从而验证了文中算法的有效性。

智能浮体; 基于概率推理的学习控制; 定点控制; 轨迹跟踪

0 引言

随着各国对海洋开发的重视, 针对海上安全保护、水文气象信息采集及海面搜救等方面的需求大幅增加, 开发一种自主性强、灵活度高、可重构的海面智能浮体(autonomous surface vehicle, ASV)平台至关重要。如图1所示, 多个浮体拼接成不同形状以适应不同作业场景, 可快速形成柔性运输通道、自动浮桥搭建和形成作业平台等, 也可以抵抗更大的干扰以提高系统稳定性。为解决在运河中运输货物和废弃物的问题, 2016年, 麻省理工学院智慧城市实验室启动了“Roboat”项目, 目标是使多个浮体可以自主拼接成浮动平台, 以适应阿姆斯特丹城市中复杂的航道, 完成河道运输任务[1]。“Roboat”项目的应用也使得对智能浮体的研究越来越深入。智能浮体的优点是自主性强, 运动灵活, 多浮体可拼接成不同形状以完成不同的任务。智能浮体不仅需要具备较强的机动性和灵活性, 也需要具备先进的控制策略, 因此对单浮体运动控制的研究是完成可重构目标的基础。

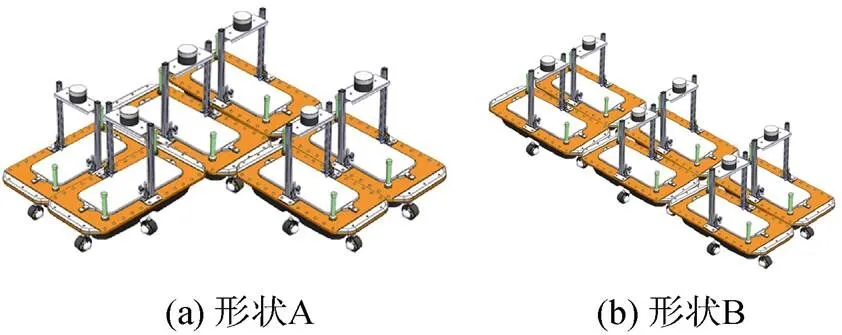
图1 小型智能浮体集群

智能浮体因较强的机动性和灵活性需要合理配置推进器。Lu等[2]所使用的浮体采用一个推进器用于驱动, 一个舵机实现转向, 这也是目前较常见的方案, 缺点是浮体有较大的转弯半径, 也无法单独对航向进行调整, 灵活性较差。Woo等[3]设计的浮体安装了2个推进器, 且左右对称, 通过分别控制推力的大小实现前进和转向, 虽然浮体航向可以灵活调整, 但无法完成横荡运动。Paulos等[4]使用的浮体采用了四推进器方案, 推进器呈“X”型分布, 浮体可实现纵荡、横荡和艏摇运动, 浮体的灵活性大大提高。Wang等[5]在浮体中使用了4个呈“+”型分布的推进器, 该浮体机动性强, 推进器效率更高。单浮体是一个多输入、多输出的非线性系统, 多浮体拼接后动力学模型也发生了变化, 推进器数量随着拼接浮体数量的增加而增多, 且浮体的工作环境复杂多变, 因此开发高性能控制器将面临巨大的挑战。Park等[1]利用四推进器浮体, 提出了一种多浮体可重构的反馈控制系统, 每个浮体都可以锁定到其他浮体, 形成相连的刚性体, 提高了对环境的适应能力。Wang等[5]提出了非线性模型预测控制(nonlinear model predictive control, NMPC)方案, 在室内水池中进行了浮体运动控制的实验。随着理论和技术的逐步发展, 特别是在强化学习和深度学习方面, 无人系统的发展得到了极大的提升。Mnih等[6]提出了一个深度学习模型, 可以直接从高维感知输入中学习控制策略, 该方法具备通用性, 但只能学习短时间内的经验, 无法学习长时间的控制策略, 且网络不一定能够收敛, 需要对深度网络的参数不断进行优化调整。Lu等[2]根据深度确定性策略梯度(deep deterministic policy gradient, DDPG)算法提出了一种基于无模型强化学习控制器, 该控制器经过反复的路径跟踪训练和实验, 验证了该方法具备路径跟踪和自主学习能力。Deisenroth等[7]提出一种学习控制的概率推理(pr- obabilistic inference learning to control, PILCO)方法, 基于模型强化学习算法在连续状态动作域中实现了数据的高效利用, 可直接应用于物理系统。Ramirez等[8]探讨了基于PILCO算法学习控制欠驱动自主水下航行器的能力, 通过少量的现场实验来优化控制策略, 不足之处是未考虑给定模型与实际模型不一致的情况, 且仿真实验中未考虑水流扰动对结果的影响。基于无模型强化学习方法不需要建立模型, 智能体的所有决策都是通过与环境交互得到的, 需要大量试错, 数据的利用率低, 而且当环境发生变化时, 需要重新进行学习, 不具备泛化能力。而基于模型强化学习方法可以利用已有的数据学习系统模型, 利用学习到的模型预测其他未知状态。相比无模型强化学习, 基于模型强化学习具有较强的泛化能力[9]。

文中以四推进器智能浮体的建模和控制器设计为核心展开研究, 将基于模型强化学习理论应用于控制器设计中, 使浮体在有水流扰动或采用近似动力学模型的情况下, 通过少量实验快速学习控制策略, 并完成定点控制及轨迹跟踪的目标, 可为海上大型浮体协同控制提供参考。

1 智能浮体动力学模型建立

1.1 智能浮体推进器配置

使用四推进器的小型浮体进行实验分析, 通过4个推进器的配合能够确保浮体的灵活性和稳定性。对浮体建立大地坐标系和运动坐标系O-XYZ, 系统结构如图2所示。

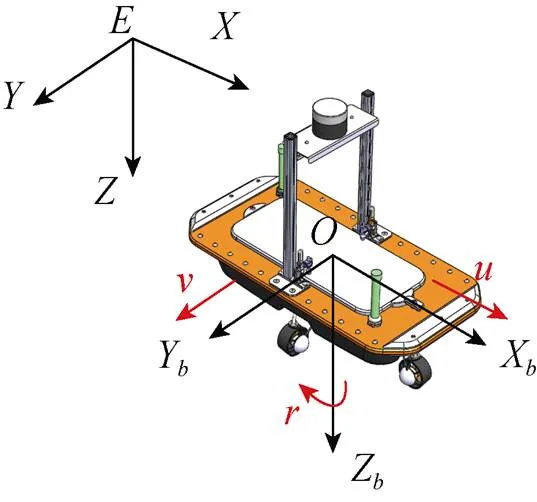
图2 智能浮体系统结构图

文中的智能浮体由4个推进器(1～4)组成, 能够完成纵荡()、横荡()以及艏摇()运动, 推进器分别位于浮体4条边的中点处, 呈“+”型分布, 如图3所示, 箭头指向表示推力正方向。

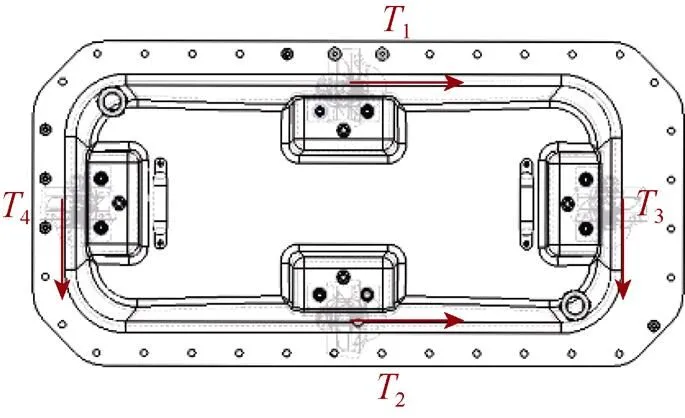
图3 智能浮体推进器分布

对于智能浮体水平方向的控制有下述关系

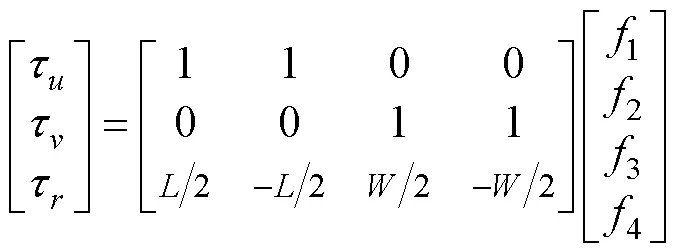
1.2 动力学模型

根据Fossen[10]所提出的流体中刚体动力学公式, 建立浮体的动力学模型为

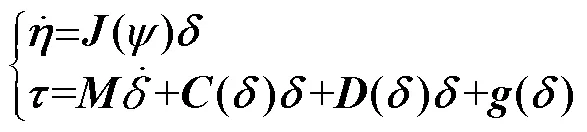
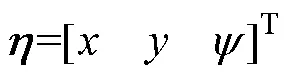
运动坐标系向大地坐标系的变换矩阵

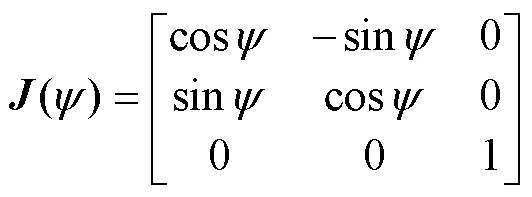
运动坐标系下智能浮体线速度和角速度向量

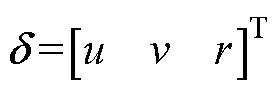
智能浮体惯性矩阵

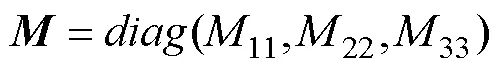
假定运动坐标系原点与浮体重心重合, 则智能浮体的科里奥利项与向心项的斜对称矩阵

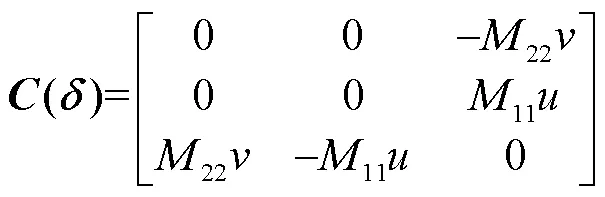
考虑智能浮体的运动速度较小, 且相对于长、宽的中轴线对称, 则智能浮体流体阻力矩阵

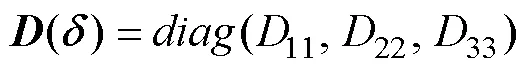
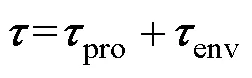
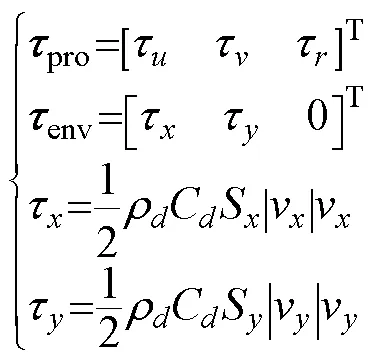
通常当浮体的航行速度较慢时, 可以将其的动力学模型近似为一个线性模型

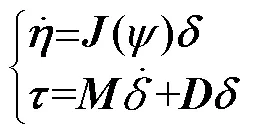
经变形可得

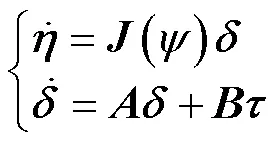
2 基于PILCO算法的控制器设计

2.1 PILCO算法基本原理

PILCO算法是基于模型的策略搜索方法, 把模型误差纳入考虑范围, 将模型不确定性视为时间上不相关的噪声, 它解决模型偏差的方法不是集中于一个单独的动力学模型, 而是建立了概率动力学模型[8]。PILCO算法的层次结构如图4所示。

图4 PILCO算法层次结构图

PILCO算法的结构可分为以下3层。

1) 底层: 学习一个状态转移的概率模型。

假定系统的动力学模型表示为

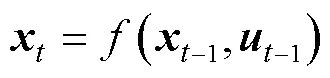
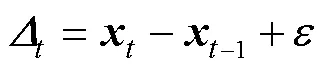
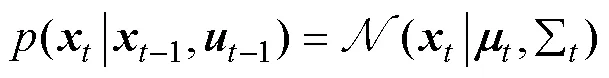
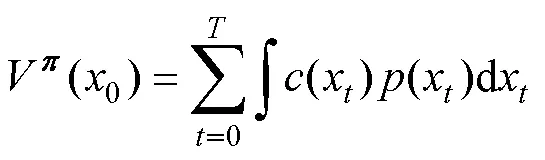
PILCO算法的伪代码表示如下:

2: loop;

3: 执行控制策略;

4: 记录收集的经验;

5: 学习概率动力学模型;

6: loop;

9: 进行策略优化;

10: end loop;

11: end loop。

2.2 控制器设计

基于PILCO算法原理, 智能浮体的控制策略优化分为以下2个阶段。

1) 获取初始控制策略

首先对给定模型加入随机策略产生初始数据, 并学习概率动力学模型。文中被控对象是四推进器的智能浮体, 在每一个控制周期产生的随机控制策略定义为

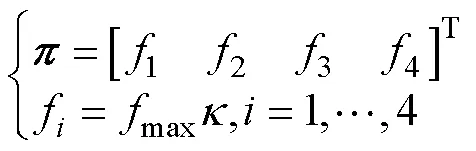
2) 控制策略优化

将初始控制策略应用于实际智能浮体中, 将获得的实际数据继续训练概率动力学模型, 并通过策略搜索方法优化控制策略, 从而获得更好的控制效果。

为加快控制策略网络的学习速度, 满足实时性应用的要求, 控制策略网络采用径向基函数(radical basis function, RBF)神经网络。控制策略表示为

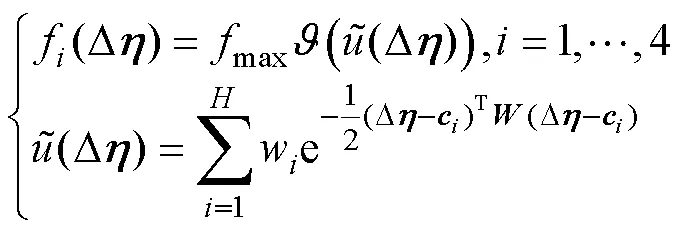
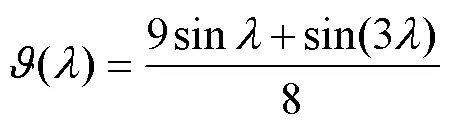
基于PILCO算法的控制器设计如图5所示。概率动力学模型为高斯模型, 给定模型为被控对象建立的动力学模型, 在实际应用中, 该模型与实际模型存在一定的误差。

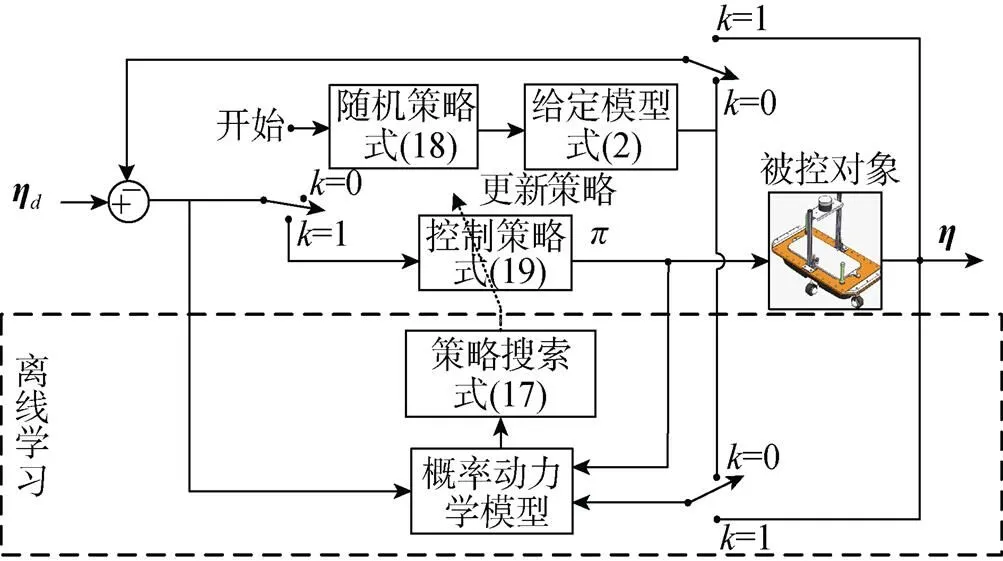
图5 基于PILCO算法的控制器结构框图

由图5可得, 初始状态时=0, 对给定的动力学模型输入随机控制策略产生初始随机数据, 经过训练获得初始高斯模型; 策略搜索算法使成本函数最小以产生控制策略; 然后将置为1, 生成的策略在实际机器人模型上进行测试, 并获得数据再次进行策略优化。

2.3 NMPC与PILCO控制器对比

NMPC在工程上已有较成功的应用, 该控制算法是经典与现代控制的结合, 在处理多变量约束问题上是一种十分有效的方法[11]。NMPC的结构框图如图6所示。

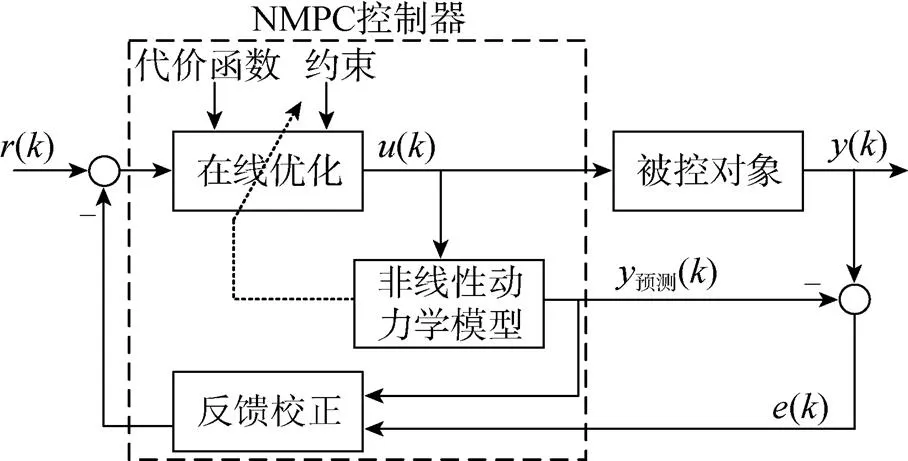
图6 NMPC结构框图

对比图5和图6可知, NMPC与PILCO控制器的共同点是: 两者均需要一个给定模型。NMPC控制器利用给定模型预测系统的未来响应; PILCO控制器利用给定模型获取初始数据, 并建立概率动力学模型。

当给定模型与实际模型一致时, NMPC控制器的预测输出与实际系统输出相同, 通过在线优化获得较好的控制策略; PILCO控制器利用给定模型产生数据拟合一个概率动力学模型, 加快控制策略的学习, 并优化控制策略。

PILCO控制器提高了数据的利用率, 通过离线学习能够不断优化控制策略; 而经典的NMPC控制器在求解多变量非线性系统是一种有效方法, 但对给定模型的精度有一定的要求, 且模型精度越高, 控制效果越好。为验证PILCO控制器在智能浮体运动控制上的有效性, 并展示PILCO控制器具备的学习能力, 设计仿真实验对比NMPC控制器与PILCO控制器在智能浮体运动控制上的控制效果。

3 仿真实验与分析

3.1 仿真条件

智能浮体的模型参数如表1所示[5], 流体阻尼公式的参数如表2所示。

表1 浮体模型参数

表2 流体阻尼公式参数

仿真实验选用的电脑处理器为Intel Core i5- 3470 3.20 GHz, 内存8 GB; MATLAB 2019b。

3.2 实验设计

首先在算法结构和训练过程上对比了PILCO算法与DDPG算法, 其次对浮体的运动控制设计了3组实验, 对比了PILCO算法与NMPC算法的控制效果。

PILCO算法是一种基于模型强化学习算法, 可根据先验知识建立的动力学模型大大提高数据的利用率及学习的速度。而DDPG算法是一种基于无模型强化学习算法, 可应用于连续系统的控制中, 通过自学习对复杂控制任务具备较强的控制能力。但需要与环境不断进行交互与试错, 学习速度慢且对数据的利用率低[12]。在相同硬件条件下, DDPG算法应用在智能浮体的运动控制上, 与PILCO算法的结果对比如表3所示。

表3 PILCO算法与DDPG算法对比

DDPG算法存在学习速度慢, 数据利用率低等问题, 而PILCO算法的优势在于:

1) 根据先验知识对被控对象初步建立模型, 并从给定模型中产生训练数据, 该方法大大提高了数据的利用率;

2) PILCO算法不直接对系统的动力学建模, 而是引入一个差分变量, 与直接学习函数值相比, 学习差分更有优势, 因为相邻周期内, 状态的变化较小, 学习差分近似于学习函数的梯度, 加快了学习的速度。

文中选择PILCO算法设计强化学习控制器, 共设计了3组对比实验, 分别是:

1) 当给定的预测模型与真实系统模型一致, NMPC与PILCO控制器的定点控制与轨迹跟踪仿真结果对比;

2) 在实验1的基础上, 在环境中加入在和方向、大小均为0.3 m/s的水流, 验证在固定水流干扰下, 2种控制器的控制结果;

3) 考虑当动力学模型建立不准确时, 验证PILCO控制器具备学习控制的能力。

NMPC控制器设计采用MATLAB提供的非线性模型预测控制工具箱, 具体参数如表4所示, 其他参数均使用工具箱默认设置。

表4 NMPC控制器参数

3.2.1 静水环境

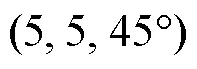
由图7可知, 当预测模型及给定模型与实际模型一致, NMPC与PILCO控制器均能较好地控制智能浮体到达目标位置, 这表明了PILCO控制器在给定模型精确的情况下, 通过策略搜索获得的初始策略能够完成定点控制的目标, 且控制效果与NMPC控制器的结果接近。

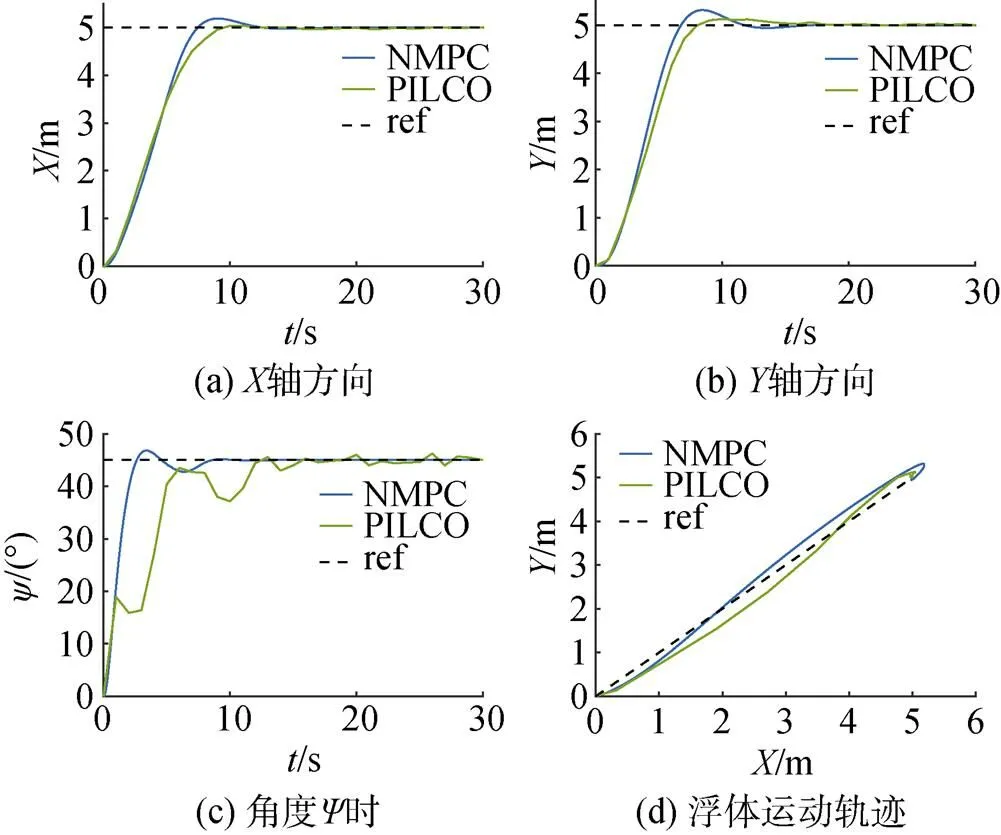
图7 给定模型与实际模型一致时仿真结果对比曲线

在无水流干扰时, PILCO控制器在初始控制策略下具备一定的轨迹跟踪能力。当给定跟踪目标为正弦轨迹时, NMPC控制器与PILCO控制器的仿真结果如图8所示。

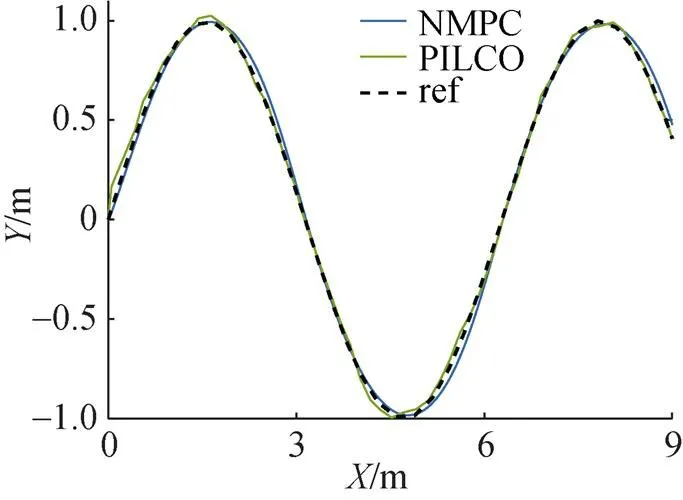
图8 无水流干扰时跟踪正弦轨迹曲线

由图8可知, 在没有水流干扰且给定目标轨迹为正弦轨迹时, NMPC控制器与PILCO控制器的控制误差均较小, 控制效果接近, 均能够完成轨迹跟踪的目标。通过在静水环境中2组仿真实验可以得到: 当给定模型与真实模型一致时, PILCO控制器具备较好的控制性能, 可以完成定点控制和轨迹跟踪的目标。

3.2.2 水流扰动环境

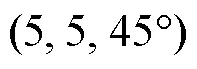
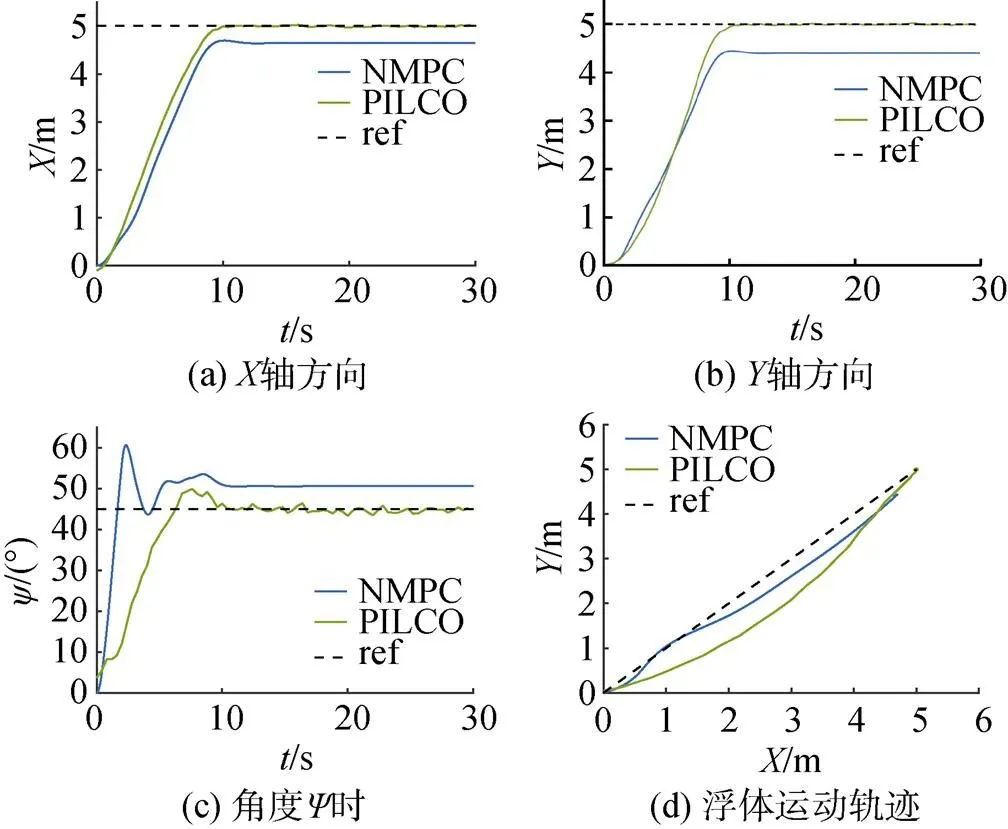
图9 0.3 m/s水流扰动下仿真结果对比曲线

由图9分析可得, 当浮体受到水流扰动时, 水流大小0.3 m/s, 根据流体阻尼公式计算可得, 水流对浮体产生的阻力最大达到4.32 N, 而推进器在同一方向最大推力为10 N, 水流最大阻力占推进器最大推力的43.2%。在给定模型中未考虑水流干扰模型, 通过仿真分析可得, NMPC控制器由于存在较大的环境扰动, 不能准确到达目标位置, 在,及航向角控制上均存在一定的稳态误差, 而PILCO控制器经过对运行数据的收集并学习后, 能够克服环境扰动到达目标位置, 且稳态误差小于0.1 m, 运动路径也接近起点至终点的直接路径。

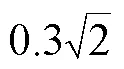
浮体跟踪正方形轨迹比跟踪正弦轨迹更有挑战, 分析图10可得, 在有水流干扰情况下, 浮体共进行了5次实验。第1次跟踪目标轨迹存在较大误差, 通过对控制策略的优化, 浮体的运动轨迹逐渐接近参考轨迹, 能够完成跟踪正方形轨迹的目标。这表明PILCO控制器具备一定的学习控制能力, 能够通过对控制策略的不断优化, 克服环境的扰动并获得更优的运动轨迹。

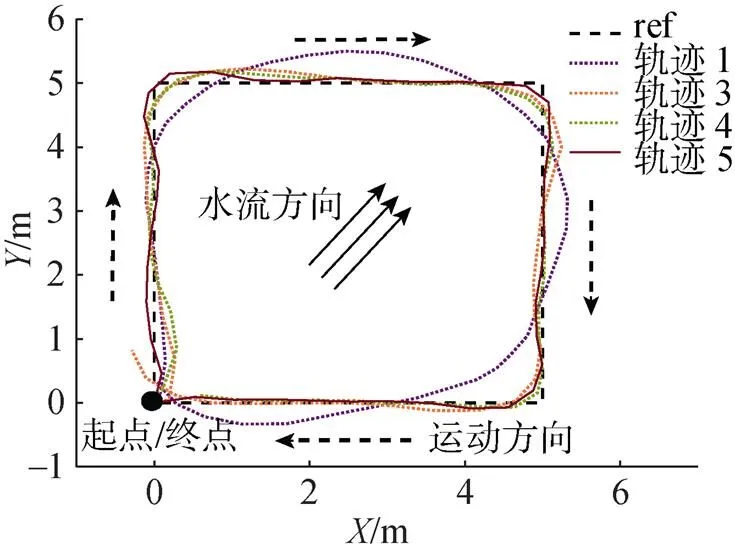
图10 跟踪正方形轨迹学习结果

3.2.3 给定模型为近似模型

模型预测控制需要一个描述对象动态行为的模型, 该模型的作用是预测系统未来的动态, 所以经典NMPC控制器对给定模型有一定要求, 模型越精确控制效果越好。然而, 对智能浮体的精确建模存在一定的困难, 在该仿真实验中, 讨论了当动力学模型简化为线性模型时, PILCO控制器的学习控制能力。

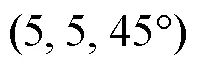
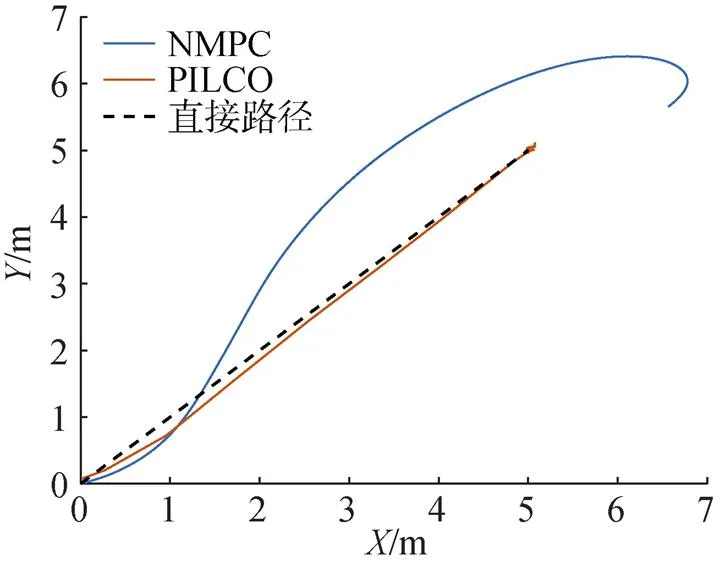
图11 给定模型与实际模型不一致时仿真结果对比曲线

分析图11可得, 如果内部模型建立不准确或者仅以一个线性模型做近似替代, NMPC控制器的控制将不能完成定点控制的任务, 而PILCO控制器能够完成定点控制的目标, 并获得较好的控制效果, 表明了PILCO控制器不依赖被控对象的精确模型, 即便模型误差较大, PILCO控制器也能够在运行过程中快速学习到控制策略。PILCO控制器学习过程代价函数的变化如图12所示。

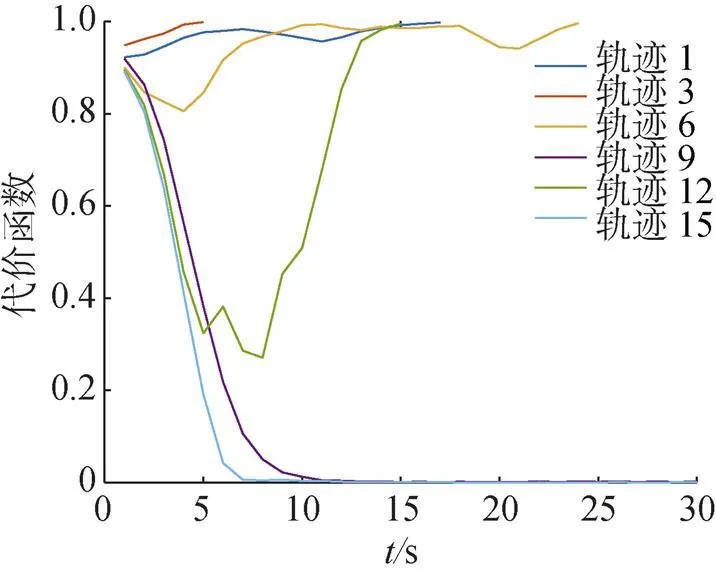
图12 PILCO学习过程代价函数变化曲线

由图12可得, 在给定模型与实际模型有较大差异的情况下, PILCO控制器能够在运行过程中不断学习, 代价函数值逐渐变小, 表明智能浮体的运动轨迹越接近目标轨迹。经过15次的训练后, PILCO控制器已经达到一个较好的控制效果, 而NMPC控制器在预测模型存在较大误差时, 不能准确到达目标位置。

4 结束语

为提高智能浮体的灵活性, 使其具备一定学习控制的能力, 文中采用了一种基于PILCO算法的控制器设计方法, 研究了PILCO算法在控制过驱动智能浮体的适用性, 并在MATLAB上进行了仿真验证。采用的控制器把模型误差纳入考虑范围, 建立了概率动力学模型, 提高了浮体的自适应性。针对水流扰动、模型建立不准确的情况, 提供一种解决浮体运动控制问题的新思路。对比PILCO控制器与NMPC控制器的控制结果可得: 在静水和水流干扰情况下, PILCO控制器可以在少量的实验中使浮体学习到控制策略, 完成定点控制, 并且具备较好的轨迹跟踪能力; 当被控对象以简单的线性系统代替非线性系统时, 该控制器经过一定次数的学习, 能够不断优化控制策略, 提高了控制器性能。下一步将对该控制器在真实浮体中进行实物测试, 并进行多浮体的协同控制研究。

[1] Park S, Kayacan E, Ratti C, et al.Coordinated Control of a Reconfigurable Multi-vessel Platform: Robust Control Approach[C]//2019 International Conference on Robotics and Automation(ICRA).Montreal, Canada: IEEE, 2019.

[2] Lu Y, Zhang G, Qiao L, et al.Adaptive Output-feedback Formation Control for Underactuated Surface Vessels[J].International Journal of Control, 2020, 93(3): 400-409.

[3] Woo J, Yu C, Kim N.Deep Reinforcement Learning-based Controller for Path Following of an Unmanned Surface Vehicle[J].Ocean Engineering, 2019, 183: 155-166.

[4] Paulos J, Eckenstein N, Tosun T, et al.Automated Self-assembly of Large Maritime Structures by a Team of Robotic Boats[J].IEEE Transactions on Automation Science and Engineering, 2015, 12(3): 958-968.

[5] Wang W, Mateos L A, Park S, et al.Design, Modeling, and Nonlinear Model Predictive Tracking Control of a Novel Autonomous Surface Vehicle[C]//2018 IEEE International Conference on Robotics and Automation(ICRA).Brisbane, Australia: IEEE, 2018: 6189-6196.

[6] Mnih V, Kavukcuoglu K, Silver D, et al.Playing Atari with Deep Reinforcement Learning[J].arXiv, (2013-12-19) [2021-09-01].https://arxiv.org/abs/1312.5602.

[7] Deisenroth M, Rasmussen C E.PILCO: A Model-based and Data-efficient Approach to Policy Search[C]// Proceedings of the 28th International Conference on Machine Learning(ICML-11).Bellevue, Washington, USA: ICML, 2011: 465-472.

[8] Ramirez W A, Leong Z Q, Nguyen H D, et al.Exploration of the Applicability of Probabilistic Inference for Learning Control in Underactuated Autonomous Underwater Vehicles[J].Autonomous Robots, 2020, 44(6): 1121-1134.

[9] 郭宪.深入浅出强化学习: 原理入门[M].北京: 电子工业出版社, 2018.

[10] Fossen T I.Guidance and Control of Ocean Vehicles[M].New Jersey: John Wiley & Sons, 1994.

[11] 陈虹, 刘志远, 解小华.非线性模型预测控制的现状与问题[J].控制与决策, 2001, 16(4): 385-391.

Chen Hong, Liu Zhi-yuan, Xie Xiao-hua.Nonlinear Model Predictive Control: The State and Open Problems[J].Control and Decision, 2001, 16(4): 385-391.

[12] Lillicrap T P, Hunt J J, Pritzel A, et al.Continuous Control with Deep Reinforcement Learning[EB/OL].ArXiv, (2015 -09-01) [2021-09-01].https://www.researchgate.net/publ- ication/281670459_Continuous_control_with_deep_rein- forcement_learning.

Motion Control Method of Autonomous Surface Vehicle Based on the PILCO Algorithm

ZHANG Shang1, YANG Rui1,2, CHEN Zhen1,2, LI Ming1,2

(1.College of Engineering, Ocean University of China, Qingdao 266100, China; 2.Shandong Marine Intelligent Equipment Technology Engineering Research Center, Qingdao 266100, China)

A highly autonomous, flexible, and reconfigurable autonomous surface vehicle(ASV) must be developed to fulfill the needs for ocean exploration.In this study, an ASV composed of four thrusters is analyzed by establishing the dynamic model of the ASV, designing its controller based on the probabilistic inference learning to control(PILCO) algorithm, and conducting simulation experiments of fixed-point control and trajectory tracking.The simulation results show that the ASV model can autonomously learn the control strategy in a small number of experiments and realize motion control during a water flow disturbance or when using an approximate dynamic model, thereby verifying the effectiveness of the proposed algorithm.

autonomous surface vehicle(ASV); probabilistic inference learning to control(PILCO); fixed-point control; trajectory tracking

张尚, 杨睿, 陈震, 等.一种基于PILCO算法的智能浮体运动控制方法[J].水下无人系统学报, 2021, 29(5): 541- 549.

U674.38; TP242.6;TP181

A

2096-3920(2021)05-0541-09

10.11993/j.issn.2096-3920.2021.05.005

2020-10-20;

2020-12-17.

国家自然科学基金项目资助(51709245); 国家重点研究发展计划项目资助(2017YFC1405203).

张 尚(1996-), 男, 在读硕士, 主要研究方向为海上可重构智能浮体控制系统研究.

(责任编辑: 杨力军)