基于数据挖掘的上市公司高送转预测研究

江琛，夏晓玲，吴伟，崔海波，马传香

(1.湖北大学计算机与信息工程学院， 湖北 武汉 430062； 2.湖北省教育信息化工程研究中心， 湖北 武汉 430062)

0 引言

送转是上市公司给各个股东分红的一种方式，将股份公司的盈余公积金或者未分配利润转化为股份，将分红作为股票给予股东，将盈余公积金或利润以股票的形式留在公司.而高送转指的是送转比例达到0.5及以上的股票.一般认为，“高送转”除了暗示公司经营业绩的良好表现，往往还预示着公司会有较大的发展和成长，传递公司未来发展前景的良好信息，增强投资者的信心[1].

对高送转股票的预测对投资者具有极重大的经济学意义.目前，在我国股票市场中，中小型投资者比较多，中小型投资者在信息获取和甄别方面以及专业知识方面处于弱势地位，这增加了他们识别那些真正具有投资价值的“高送传”公司的难度，本研究从不同投资者的视角对高送转进行预测，提供更加具有针对性的决策支持.

石好等[2]采用逻辑回归(logistic regression)与主成分分析(principal component analysis, PCA)相结合的方法, 构建了年报高送转股票的预测模型, 模型正确率在55%以上, 预测准确度可达80.91%.蔡景波，等[3]对数据进行缺失值、异常值、标准化等数据处理，采取特征选择中过滤法、包裹法、嵌入法等方法提取特征.使用Stacking集成模型对股票是否发生高送转进行预测，其 F1得分为0.59，AUC得分为0.82.事实上，对投资者而言，得到所有的高送转股票并没有太大意义，投资者更关心的是通过数据挖掘的手段收集到的会发生高送转的股票的准确率，因此对于高送转问题而言，相对于查全率，查准率对于投资者具有更加重大的意义.

1 算法介绍

1.1 Lasso回归Lasso回归是一种基于收缩和变量选择方法的回归模型，它解决了标准回归方法中的“乐观偏差”，和“极端情况时模型表现较差”这两个问题[4].Lasso回归的特色就是可以建立广义线型模型，这里广义线型模型包含一维连续因变量、多维连续因变量、非负次数因变量、二元离散因变量、多元离散因变，除此之外，无论因变量是连续或离散的，Lasso回归都能处理，总的来说，Lasso对于数据的要求是极其低的，所以应用程度较广；除此之外，Lasso还能够对变量进行筛选和降低模型的复杂程度.复杂度调整是指通过一系列参数控制模型的复杂度，从而避免过拟合.对于线性模型来说，复杂度与模型的变量数有直接关系，变量数越多，模型复杂度就越高.更多的变量在拟合时往往可以给出一个看似更好的模型，但是同时也面临过拟合的危险.lasso回归通过约束回归系数的绝对值之和小于固定值λ，实现“压缩”回归系数趋近于零的方式减少预测误差，但实际情况下，这种方法会限制模型的复杂性[5].

1.2 PCA降维PCA是一种常见的数据分析方式，常用于高维数据的降维，可用于提取数据的主要特征分量.在某些领域的研究中会采用一种混合的PCA算法来实现降维，PCA会帮助从高维数据中识别出低维数据，以便对数据进行降维处理，这确保了数据集中冗余属性的消除[6].在训练反向传播神经网络(BPNN)体系结构之前，使用主成分分析(PCA)去关联输入数据，有助于提高BP神经网络的预测性能[7].PCA作为一种无监督降维方法，在图像处理分析领域同样被广泛认为是一种高效的预处理步骤[8].PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的.其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1、2个轴正交的平面中方差最大的.依次类推，可以得到n个这样的坐标轴.通过这种方式获得的新的坐标轴，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0.于是，余下的坐标轴可以被忽略，只保留前面k个含有绝大部分方差的坐标轴.

1.3 逻辑回归算法逻辑回归模型是一种在统计学和机器学习领域中都非常流行的模型，用于拟合二元结果和评估解释变量的统计显著性，并探寻二分类结果(例如，存活/死亡，成功/失败，是/否)与一个或多个预测因子之间的关系，这些预测因子可能是离散的或回归的[9].在卫生服务、人口和公共卫生以及流行病学的相关研究中，会经常出现多层次数据.在相关研究领域中，二元结果是非常常见的.对PubMed数据库的检索结果表明，多层或分层回归模型的使用正在迅速增加[10].

“多元逻辑回归”是一种研究多因子对二类分结果的共同影响的技术.对于多元逻辑回归，可用如下公式似合分类，在逻辑回归模型参数估计时，化简公式可以带来很多益处，y={0,1}为分类结果，如式(1)和式(2)所示：

(1)

(2)

对于训练数据集，特征数据x={x1,x2, …,xm}和对应的分类数据y={y1,y2, …,ym}，构建回归模型，y取值为0或1，可得概率如式(3)和式(4)所示：

(3)

(4)

1.4 支持向量机算法支持向量机被广泛应用于模式识别，其目标是找到具有最大余量的超平面，以减少误分类率[11].它按以下方法工作，使用一种非线性映射，把原始训练数据映射到较高的维上，并在新的维上搜索最佳分离超平面，SVM使用支持向量和余量发现该超平面.作为一个线性分类器，它和其它分类器的区别在于，SVM不仅能把样本分对，还能确保余量最大化.SVM的核心操作是两个向量做内积，公式如式(5)：

(5)

其中y为与x的输入特征向量相关联的预测类；αi是在训练过程中通过最小化二次目标函数分配给训练数据点xi的可调权重；b为偏置项；K是核函数.因此，y可以看做是训练数据点xi和目标数据点x之间相似度的加权线性组合.训练数据集中权重为正的数据点影响最终的解，称为支持向量.

SVM主要研究目标是提高训练和检验速度，使得SVM可以成为超大型数据集更可行的选择.SVM模型参数的优化也是众多学者研究的目标，文献[12]提出了一种新的切换延迟粒子群优化算法来优化支持向量机参数.支持向量机模型同样有其局限性，传统的支持向量机方法并不适用于计算数据集各属性的不同特征[13].

SVM是一种可以对线性可分和线性不可分两种类型的数据集进行分类的模型.最大边缘超平面是一个线性类边界，因此对应的SVM可以用来对线性可分的数据进行分类，称这种训练后的SVM为线性SVM；对于线性不可分的数据，不能画一条直线将两个类分开，该决策边界是非线性的.当输入的数据不可线性分离时，SVM具有非常显著的效果[11].

1.5 XGBoost算法XGBoost是boosting算法的其中一种.Boosting算法的思想是将许多弱分类器集成在一起形成一个强分类器.而所用到的树模型则是CART回归树模型.它作为一种可扩展的树增强系统，已被众多数据科学家广泛应用于各个领域，并在许多领域获取了相关的研究进展.它使用稀疏感知算法处理稀疏数据，为近似学习提供了理论上合理的加权分位数草图.并应用了多种相关技术，如缓存访问模式，数据压缩和分片等，这些技术也可以应用于其他机器学习系统[14].

CART回归树是假设树为二叉树，通过不断将特征进行分裂.比如当前树结点是基于第j个特征值进行分裂的，设该特征值小于s的样本划分为左子树，大于s的样本划分为右子树，如式(6)、(7)所示.

R1(j,s)={x|x(j)≤s}

(6)

R1(j,s)={x|x(j)>s}

(7)

而CART回归树实质上就是在该特征维度对样本空间进行划分，而这种空间划分的优化是一种NP-hard问题，因此，在决策树模型中是使用启发式方法解决.典型CART回归树产生的目标函数如式(8)所示：

∑xi∈Rm(yi-f(xi))2

(8)

该算法思想就是不断地添加树，不断地进行特征分裂来生长一棵树，每次添加一个树，其实是学习一个新函数，去拟合上次预测的残差.当我们训练完成得到k棵树，我们要预测一个样本的分数，其实就是根据这个样本的特征，在每棵树中会落到对应的一个叶子节点，每个叶子节点就对应一个分数，最后只需要将每棵树对应的分数加起来就是该样本的预测值.文献[15]将XGBoost与大多数分类方法进行了比较，XGBoost给出了相对更优的结果.文献[16]表明，XGBoost训练出的集成分类器能有效地防止过拟合，在某些领域，处理多维数据时检测结果优于SVM模型.

2 数据及数据处理

本文中数据处理流程如图1所示.

图1 数据处理流程图

2.1 实验环境本研究采用的实验环境如表1所示.

表1 实验环境

2.2 数据介绍本研究数据分为三部分：年数据、日数据、基础数据.年数据是数据的核心部分，其中含有3 466支股票7年的股市数据，共有24 262行，362列数据；日数据含有3 466支股票在这7年中每天的股市数据，共有5 899 132行数据，61列数据；基础数据中包含了这3 466支股票的上市年限、所属行业、所属概念板块数据.其中日数据与年数据中包含部分重复特征，部分无用特征和部分数据几乎全部缺失的特征.年数据中的‘会计准则’、‘货币代码’在模型中没有作用且在数据中只有一种取值，‘会计区间’，‘合并标志，1-合并，2-母公司’两列的数据同样没有任何差异.本研究以年数据为主，日数据中与年数据重复的列取年数据.基础数据中的‘上市年限’和‘所属行业’对高送转具有一定的预测意义.

2.3 数据处理将文件名改为英文，年数据文件名改为YearData.csv；日数据改为DayData.csv；基础数据改为BasicData.csv，文件读取见代码部分.

2.3.1 数据合并 年数据的shape为(24 262, 362)，年数据中包含大量缺失的列与行，在这里我们将数据缺失达到0.7以上的行与列删除，避免后期处理过程中过多的缺失值填补对预测模型造成干扰，最终剩余数据的shape为(22 551，362).然后将列名‘年份(年末)’改为‘年’以方便合并日数据和基础数据.

日数据的shape为(5 899 132, 61)，日数据中含有的部分特征是年数据中已经包含在内的，所以在这里我们将其剔除.剔除之后再求出剩余特征的每年12月份的日平均值，以‘股票编号’,‘年’两列为联合主键，年数据为主体，将年数据与日数据进行合并，合并后数据shape为(22 551, 408).

基础数据的shape为(3 466, 4)，在其中提取出‘上市年限’和 ‘所属行业’两列再次合并，所需要的注意的是对于‘上市年限’特征，其与上市时间成反比，如第七年的上市年限是1，那么第六年的上市年限便为2，第一年的上市年限则为7.特征‘所属行业’在其合并之后再进行独热编码.将其与年日数据融合后的表再次融合为一张，最终的shape为(22 551, 410).

2.3.2 使用独热编码处理‘所属行业’特征 ‘所属行业’特征是非数值型的离散化数据，需要将其整合为数值型数据.其中，独热编码是一种相对简单的对离散型数据进行数值编码的方法.独热编码即one-hot 编码，又称一位有效编码，其方法是使用N位状态寄存器来对N个状态进行编码，每个状态都有它独立的寄存器位，并且在任意时候，其中只有一位有效.它基于向量空间中的度量来进行计算，将离散的特征的取值扩展到了欧式空间，离散特征的每一个取值对应多维空间中的一个点，使得各个离散数据在数值化的时候不会产生欧式距离不等的情况出现.以地区特征为例： ‘湖北’‘湖南’‘河南’，如果将其编码为0,1,2，那么相当于默认了湖北与湖南，湖南与河南的距离为1，而湖北与河南的距离为2，这样就会给予机器学习模型错误的数据信息.而使用独热编码将该特征编码为三维特征：湖北100，湖南010，河南001，在欧氏距离上便没有了区别.使用独热编码(one-hot encoding)，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点.将离散型特征使用独热编码，会让特征之间的距离计算更加合理.

本研究中，特征‘所属行业’共用18个离散特征，分别是‘房地产业’, ‘制造业’, ‘批发和零售业’, ‘租赁和商务服务业’, ‘综合’, ‘信息传输、软件和信息技术服务业’,‘文化、体育和娱乐业’, ‘建筑业’, ‘电力、热力、燃气及水生产和供应业’, ‘卫生和社会工作’, ‘采矿业’,‘科学研究和技术服务业’, ‘交通运输、仓储和邮政业’,‘农、林、牧、渔业’, ‘水利、环境和公共设施管理业’, ‘金融业’,‘住宿和餐饮业’, ‘教育’，那么在独热编码之后便会成为18维特征，处理完成后shape为(22 551, 427).

2.3.3 通过观察法和数理统计进行特征筛选 数据中有一些没有学习意义的干扰特征，如‘货币代码’,‘会计准则’,‘会计区间’,‘合并标志，1-合并，2-母公司’,由于已经拥有了是否高送转特征，‘每股送转’特征同样为冗余特征.除此之外，‘高转送预案公告日’,‘高转送股权登记日’,‘高转送除权日’虽然与高送转密切相关，但同样无法作为因子预测下一年是否高送转.将这些筛选出的无意义特征进行删除.

此外，删除数据缺失到达0.7以上的特征，完成后数据shape为(22 551, 314).

2.3.4 计算出标签‘下一年是否发生高送转’列作为标签值 通过‘股票编号’，‘年’，‘是否高送转’三列计算出‘下一年是否发生高送转’，是为1，否为0，将其作为标签，取所有股票第七年的‘下一年是否发生高送转’列为‘nan’，第七年数据便是我们的预测对象.

2.3.5 使用Lasso回归和PCA对数据进行降维 通过特征‘年’将数据进行拆分，特征‘年’的值为7的数据为预测集，1～6为训练集.

首先使用Lasso回归处理数据的共线性问题，使用corr()函数查看数据的共线性，发现数据中存在共线性问题，于是选择使用Lasso回归消除数据中的共线性问题.使用GridSearchCV函数来计算出Lasso回归的最优参数，经过多次筛选，Lasso的alpha参数的最优值为826 812.5.随后使用Lasso回归筛选出系数不为0的特征作为对上市公司实施高送转方案有较大影响的因子.

影响因子共93个，分别为[‘固定资产合计’, ‘无息非流动负债’, ‘带息流动负债’, ‘带息债务’, ‘净债务’, ‘有形净资产’, ‘营运资本’, ‘净营运资本’,‘投入资本’, ‘毛利’, ‘经营活动净收益’, ‘价值变动净收益’, ‘息税前利润’, ‘息税折旧摊销前利润’, ‘息前税后利润’,‘扣除非经常性损益后的归属于上市公司股东的净利润’, ‘企业自由现金流量’, ‘股权自由现金流量’, ‘折旧与摊销’,‘归属于母公司的股东权益/带息债务’, ‘货币资金’, ‘应收账款’, ‘预付款项’, ‘应收利息’, ‘其他应收款’, ‘存货’,‘其他流动资产’, ‘流动资产合计’, ‘可供出售金融资产’, ‘长期股权投资’, ‘投资性房地产’, ‘固定资产’, ‘在建工程’,‘无形资产’, ‘商誉’, ‘递延所得税资产’, ‘其他非流动资产’, ‘非流动资产合计’, ‘资产总计’, ‘短期借款’, ‘应付票据’,‘应付账款’, ‘预收款项’, ‘应交税费’, ‘应付利息’, ‘其他应付款’, ‘一年内到期的非流动负债’, ‘其他流动负债’,‘流动负债合计’, ‘长期借款’, ‘递延收益’, ‘非流动负债合计’, ‘负债合计’, ‘实收资本(或股本)’, ‘资本公积’,‘未分配利润’, ‘归属于母公司所有者权益合计’, ‘少数股东权益’, ‘所有者权益(或股东权益)合计’,‘负债和所有者权益(或股东权益)总计’, ‘销售商品、提供劳务收到的现金’, ‘收到的税费返还’, ‘收到其他与经营活动有关的现金’,‘经营活动现金流入小计’, ‘购买商品、接受劳务支付的现金’, ‘支付的各项税费’, ‘支付其他与经营活动有关的现金’,‘经营活动现金流出小计’, ‘经营活动产生的现金流量净额’, ‘收回投资收到的现金’, ‘取得投资收益收到的现金’,‘处置固定资产、无形资产和其他长期资产收回的现金净额’, ‘投资活动现金流入小计’, ‘购建固定资产、无形资产和其他长期资产支付的现金’,‘投资支付的现金’, ‘支付其他与投资活动有关的现金’, ‘投资活动现金流出小计’, ‘吸收投资收到的现金’, ‘取得借款收到的现金’,‘收到其他与筹资活动有关的现金’, ‘筹资活动现金流入小计’, ‘偿还债务支付的现金’, ‘支付其他与筹资活动有关的现金’,‘筹资活动现金流出小计’, ‘筹资活动产生的现金流量净额’, ‘汇率变动对现金及现金等价物的影响’, ‘现金及现金等价物净增加额’,‘加:期初现金及现金等价物余额’, ‘期末现金及现金等价物余额’, ‘成交金额’, ‘全部投入资本’, ‘流通市值’, ‘总市值’].

随后使用PCA主成分分析将数据降维至50维.

2.3.6 数据标准化

1)标准差标准化

使用标准差标准化对数据进行标准化处理.标准差标准化通过均值与方差对满足正态分布的数据进行处理，得到符合标准正态分布的数据，标准差标准化公式如式(9)所示.

X_st=(X-Xmean)/std

(9)

它表示的是原始值与均值的差值和标准差的比值，作为一个相对量，拥有去除量纲的功能.经过标准差标准化之后，数据的均值为0，标准差为1.均值为0后，数据分布以0为中心左右分布，即去中心化.方差为1对许多的算法更加有利，但是其缺点在于假如原始数据没有呈高斯分布，标准化的数据分布效果并不好.去中心化为进一步处理数据和机器学习打下基础，标准化更适合噪声较大的数据场景.数据标准化还可以去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或者量级的指标可以等同的参与计算.

2)离差标准化

离差标准化指的是用原值减去该特征的最小值，然后除以该特征的极差.数据经过离差标准化的处理之后特征值范围将维持在[0，1]区间之间，与其他的标准化方式相同，它同样可以消除量纲，使得数据变为纯数据，同时还可以消除变异大小因素的影响.有一些关系系数(例如绝对值指数尺度)在定义时要求对数据进行离差标准化，但有些关系系数的计算公式却没有这样要求，当选用要求进行离差标准化的算法时，先对数据进行标准化便是很有必要的.公式如下：

X_st=(X-Xmin)/(Xmax-Xmin)

(10)

本研究选用标准差标准化对数据进行标准化处理.

3 高送转预测和模型评估

3.1 高送转预测使用逻辑回归算法、支持向量机(SVM)算法、XGBoost算法分别对下一年是否发生高转送进行预测，并在测试集上统计其查准率，查全率和F1分数.图表分别如下：

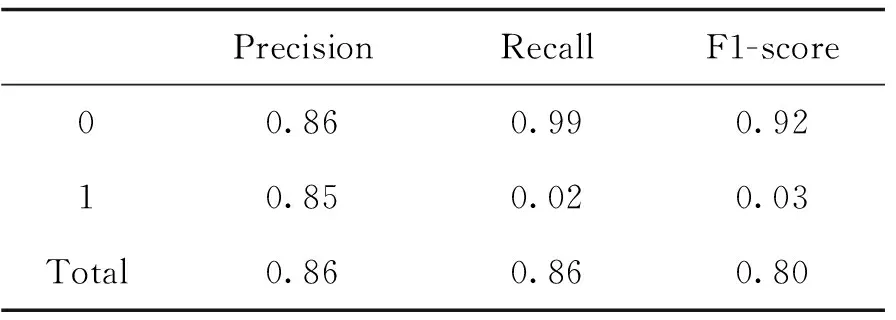
表2 逻辑回归模型的评估数据

表3 SVM模型的评估数据

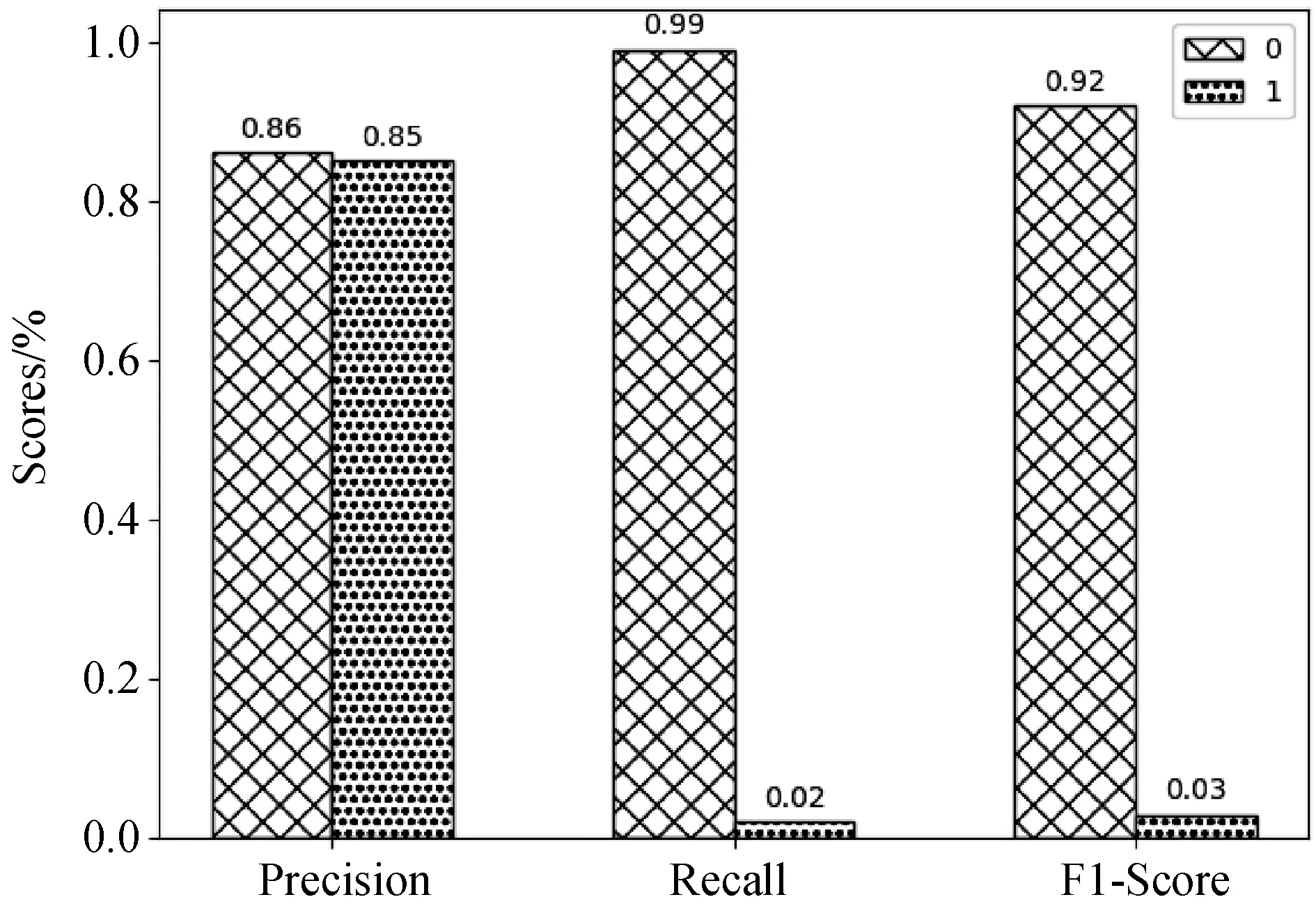
图2 逻辑回归模型预测结果图

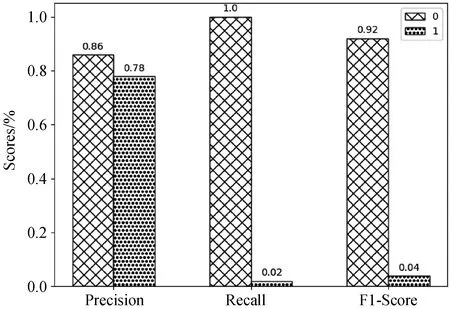
图3 SVM模型预测结果图

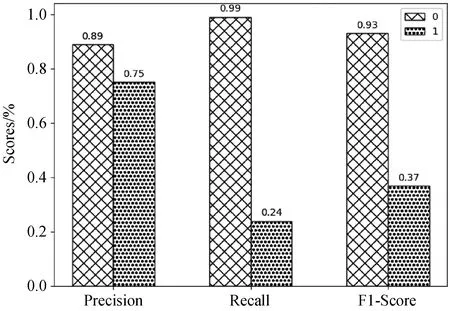
图4 XGBoost模型预测结果图

3.2 模型比较对三个算法的度量值进行比较发现，逻辑回归算法对于下一年高送转股票的查准率较高，达到0.85，但查全率过低仅有0.02；XGBoost算法的综合得分更高，在下一年高送转股票的查全率上优势较大，达到了0.24，但其查准率相对较低仅有0.75；SVM支持向量机算法没有明显优势.

表4 XGBoost算法的评估数据

因此，若想对高送转股票进行少量投资，逻辑回归算法的准确率更高，具有一定的优势，发生投资到不会发生高送转的股票的错误的概率较小.但若想对大量股票进行投资，XGBoost算法的综合能力更好，它牺牲了一点的查准率，但查全率达到了0.24，因此会有更多的股票以供选择.

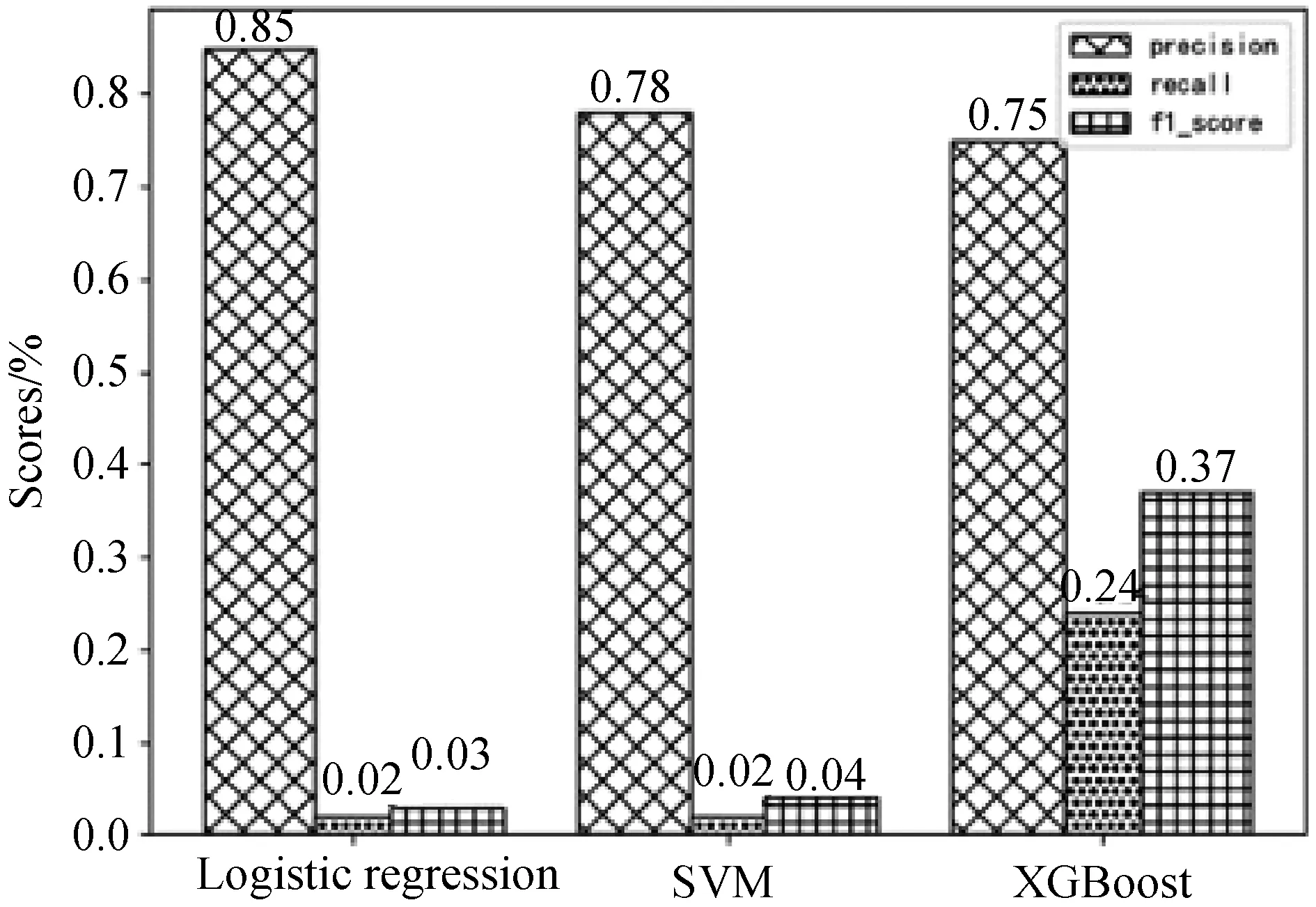
图5 模型对比图

4 结束语

在对日数据的处理上本文中采用了取每年第12月的日数据的平均值的方法，是否有更好的方法可以更好地利用日数据从而获得更多的信息值得再研究.

对‘行业’属性使用独热编码虽然做到了离散数据的数值化，并且没有掺杂冗余信息，但所获得的多维数据是一个稀疏矩阵，在特征选择与最后的模型训练的过程中行业数据并没有起到太大的作用，因此下一步工作要继续研究是否有更好的方式处理‘所属行业’数据.

使用Lasso和PCA进行特征选择和提取解决的大部分的共线性问题却没有解决全部的共线性问题，并且在实验后发现，特征提取前后对模型进行训练，模型的性能提升并不明显，因此特征选择和提取的方式在后续的工作当中可以继续优化.

在分别使用逻辑回归、SVM、XGBoost模型对高送转进行预测之后，可以得出结论：XGBoost模型的综合表现更佳，但逻辑回归模型在发生高送转上的查准率更高.

模型评估上，对下一年是否高送转的预测，投资者更加关心的是确保投资的股票会发生高送转，而不是尽可能的找出所有发生高送转的股票，因此适量的舍弃查全率追求查准率或许是一种更好的选择.