Adaptive Fuzzy Backstepping Tracking Control for Flexible Robotic Manipulator
Wanm in Chang,Yongming Li,and Shaocheng Tong,
Abstract—In this paper,an adaptive fuzzy state feedback control method is proposed for the single-link robotic manipulator system.The considered system contains unknown nonlinear function and actuator saturation.Fuzzy logic systems (FLSs)and a smooth function are used to approximate the unknown nonlinearities and the actuator saturation,respectively.By combining the command-filter technique with the backstepping design algorithm,a novel adaptive fuzzy tracking backstepping control method is developed.It is proved that the adaptive fuzzy control scheme can guarantee that all the variables in the closedloop system are bounded,and the system output can track the given reference signal as close as possible.Simulation results are provided to illustrate the effectiveness of the proposed approach.
I.INTRODUCTION
WITH the development of industrial processes automation in recent years,some of the work that based on human labor was replaced by robots in fields like medical,industrial production,military,aerospace etc.Therefore,the modeling and control design problems for the flexible robotic manipulators are of essential importance,and receiving considerable attentions.Some effective control methods concerning this issue are adaptive sliding mode technique [1],the feedback linearization method [2],the passivity approach [3],the proportional-derivative control approach [4]and so on.However,the exact dynamic model of the complex flexible joint manipulator is difficult to obtain due to the existence of the uncertainties and nonlinear terms.Thus,the fuzzy logic systems (FLSs) [5]−[10]are introduced in this paper to solve the aforementioned problem of nonlinear terms.
In recent years,some adaptive fuzzy backstepping control schemes have been developed for the robotic manipulator systems[11]−[12].However,the adaptive fuzzy control strategies in [11]−[12]are based on the traditional backstepping design technique that is subject to the so called ”explosion of complexity”problem,which is caused by repeated differentiations of virtual signals.To cope with this problem,a commandfiltered-based fuzzy adaptive backstepping control scheme is proposed in [13]−[17]for a class of nonlinear systems by introducing error compensation signals.
It is noted that many engineering systems are often driven by the actuator.Because of the physical limitations of the actuator,the actuator’s output cannot be arbitrarily large,which results in the saturation nonlinearity in the actuator.The physical plants may even experience catastrophic accidents when the actuator’s saturation is not well addressed[18]−[24].Although many adaptive intelligent control methods for the single-link robotic manipulator system have been proposed,there are no results on fuzzy adaptive backstepping control of the flexible robotic manipulator with actuator saturation,which motivates the current study.
In this paper,a command-filter-based adaptive fuzzy backstepping control scheme is designed to achieve accurate trajectory tracking for a single-link flexible manipulator in presence of actuator saturation.The proposed adaptive fuzzy backstepping control approach can guarantee that all the signals in the closed-loop system are bounded,but also the system output can track a given reference signal as close as possible.Simulation results are given to further validate the effectiveness of the proposed control method.
II.PROBLEM STATEMENT AND PRELIM INARIES
A.System Descriptions
The dynamic equation of single-link robotic manipulator coupled with a brushed direct current motor based on a nonrigid joint (Fig.1) is expressed as follows
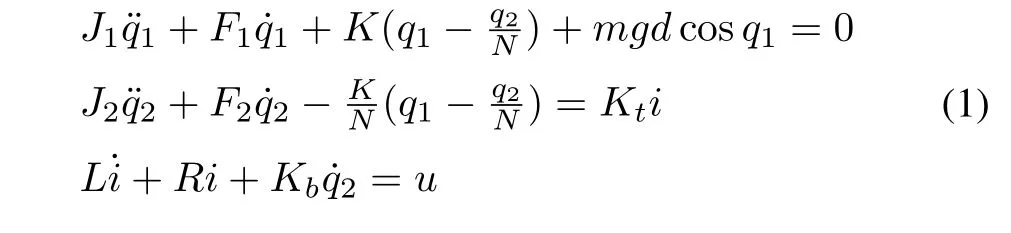
whereJ1andJ2are the inertias,q1is the angular positions of the link,q2is the motor shaft,RandLare the armature resistance and inductance respectively.iis the armature current,Kis the spring constant,K tis the torque constant,u(v)is the armature voltage,gis the acceleration of gravity,dis the position of the link’s center of gravity,F1andF2are the viscous friction constants,K bis the back-em fconstant,Mis the link mass,andNis the gear ratio.

Fig.1.Single link flexible joint robot.

System (2) is equivalent to the following pure-feedback form

Note that system (3) is of pure-feedback nonlinear form,we introduce the butterworth low-pass filter (LPF) [24]to transform system (3) to

wherex3,f=HL(s)x3≈x3,x5,f=HL(s)x5≈x5,uf=HL(s)u ≈u,HL(s) is a butterworth low-pass filter (LPF).The corresponding filter parameters of Butterworth filters with the cut off frequencywc= 1 rad/s for different values ofncan be obtained as in [24].
It should be mentioned that most actuators have lowpass properties,and the Butterworth low-pass filter (LPF) is used to eliminate the interference of high frequency signals.Furthermore,owing to the physical limitations of a DC motor,the armature voltage will no longer change when the voltage increases to a certain extent,namely the DC motor rotor voltageu(v(t)) reaches saturation.
According to [25]−[27],u(v(t)) denotes the plant input subject to saturation type nonlinearly,which is described as follows:

whereuNis the bound ofu(v(t)).Clearly,the relationship between the applied controlu(v(t))and the control inputv(t)has a sharp corner when|v(t)|=uN.Thus backstepping technique cannot be directly applied.Therefore,the saturationsat(v(t)) can be approximated by the following smooth function.

Then,saturationu(v(t)) in (5) becomes
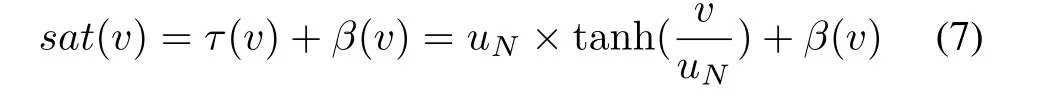
whereβ(v) =sat(v)−τ(v) is a bounded function in time and its bound can be obtained as
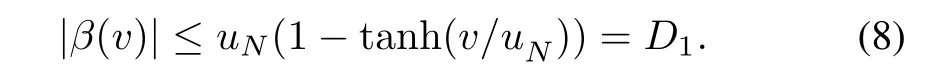
In this section,0≤|v(t)| ≤uNthe boundβ(v) increases from 0 toD1as|v(t)|changes from 0 touN,and outside this range,the boundβ(v) decreases fromD1to 0.
The control objective of this study is to design an adaptive fuzzy controller such that the system output angular positionycan track the reference signalyras close as possible.Moreover,all the signals that are involved in the resulting closed-loop system are bounded.
Before further proceeding,the following Lemma is first introduced.
Lemma 1 [13],[14]:The command filter is defined as

B.Fuzzy Logic Systems
A fuzzy logic system (FLS) consists of four parts: the know ledge base,the fuzzifier,the fuzzy inference engine working on fuzzy rules,and the defuzzifier.The know ledge base for FLS comprises a collection of fuzzy If-then rules of the following form:


The common form of fuzzy logic systems is described asy(x)=θT ϕ(x).
Lemma 2 [28]−[30]:Letδ(x) be a real smooth function defined on a compact set Ω⊆RN,and for a positive constantε,there exists a FLSy(x)=θT ϕ(x) such that

According to [28],[29],we define the optimal parameter as

Then,one has

whereεis the fuzzy minimum approximation error satisfying|ε|≤ε∗.
III.ADAPTIVE FUZZY CONTROL DESIGN AND STABILITY ANALYSIS
In this section,an adaptive fuzzy state-feedback controller,compensating signals and parameter adaptive laws are obtained by utilizing command filter backstepping technique.The stability of the closed-loop system is proved by Lyapunov function stability theory [31]−[33].
The 5-step adaptive fuzzy backstepping state feedback control design is based on the following changes of coordinates:

whereλi(i=1,...,5) are the tracking errors for command filter,xi,care the outputs of command filter,αi−1are the inputs of command filter.The purpose of the compensating signalsriis to reduce the effect of the errors (xi+1,c −αi),which is caused by the command filter.yris the desired trajectory,viare the compensating tracking error signals and¯λis an auxiliary function,which will be given in Step 5.The command filter is defined as:

whereω >0 andς ∈(0,1]are parameters to be designed,xi,c(t) =κ1(t) is the output of each filter,and the initial conditions areκ1(0)=αi(0) andκ2(0)=0.
Step 1:The time derivative ofv1is
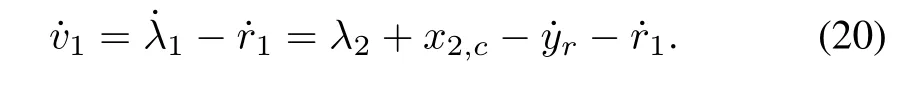
Consider the following Lyapunov function candidate:

The time derivative ofV1is

Choose the first intermediate control functionα1and the compensating signal1as
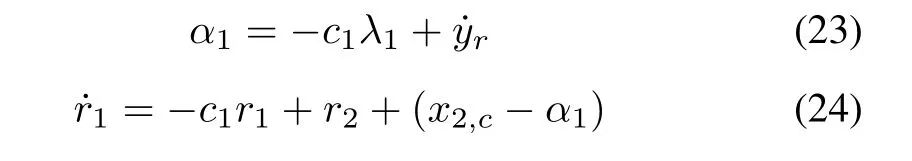
wherec1>0 is a parameter to be designed.
By substituting (23)−(24) into (22),we have

Step 2:From (16)−(17),the time derivative ofv2is
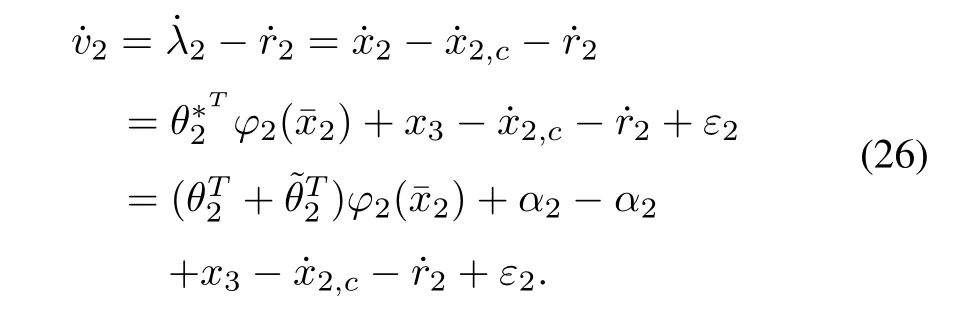
Consider the following Lyapunov function candidate:
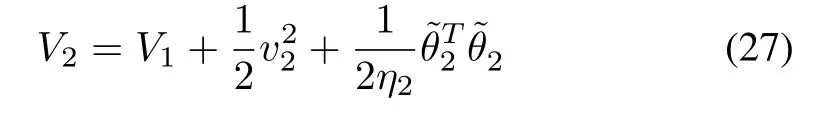
whereη2>0 is a parameter to be designed.
The time derivative ofV2is


Substituting (29) into (28) results in

Choose the intermediate control functionα2,the compensating signaland the parameter adaptation lawas

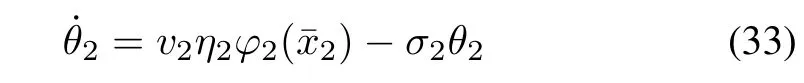
wherec2>0 andσ2>0 are design parameters.
By substituting (31)−(33) into (30),we have
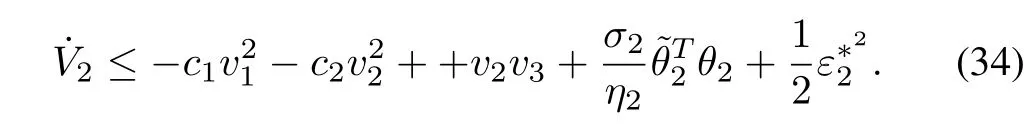
Step 3:Similar to step 2,from(16)−(17),the time derivative ofv3is
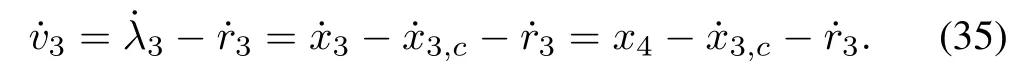
Consider the following Lyapunov function candidate:
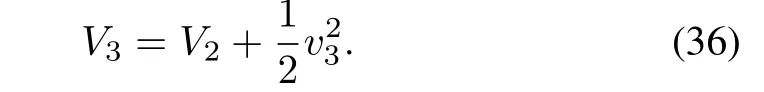
The time derivative ofV3is

Choose the intermediate control functionα3and the compensating signal3
由于长期的构造活动及地台隆起,区内发生了一系列不同期次强烈而频繁的岩浆活动,尤其是燕山期,大规模花岗岩浆活动形成了构造热蚀变的成矿背景,热液流体携带金及多金属元素在火山机构及其附近初步富集,同时,岩浆活动的巨大热能及区域性的多期多阶段的断裂构造活动使丰度值高的太华群中的金被活化,通过不断淋滤、汲取,形成富含矿质的热流体,随后由于大气降水沿构造裂隙下渗,与沿断裂构造向上运移的含矿热流体发生混合,成矿系统开放,在合适的物理化学环境下,在有利部位金富集沉淀成矿,形成构造蚀变岩型金矿床。

Substituting (38)−(39) into (37) results in

Step 4:From (16)−(17),the time derivative ofv4is
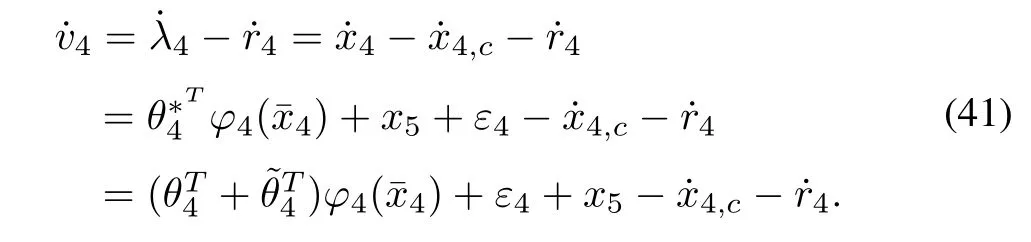
Consider the following Lyapunov function candidate:

From (41)−(42),the time derivative ofV4is

By using Young’s inequality,we have

Substituting (44) into (43) results in

Choose the intermediate control functionα4,the compensating signal4and parameter adaptation law4as

Substituting (46)−(48) into (45) results in
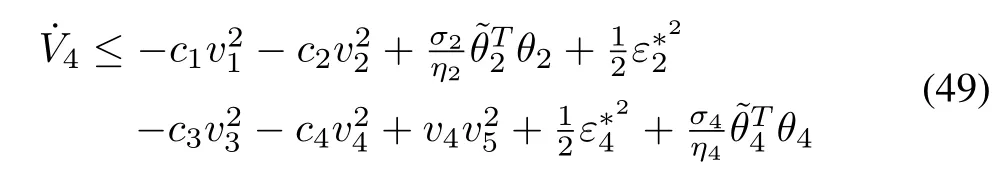
Step 5:The time derivative ofv5is

Consider the following Lyapunov function candidate:

From (50)−(51),the time derivative ofV4is

By using Young’s inequality,we have
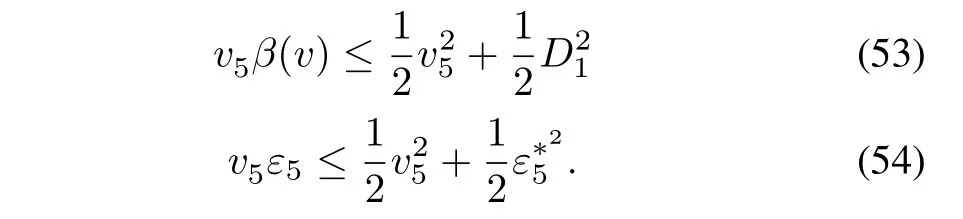
Choose the controllerv,the compensating signal5and parameter adaptive law5as

By substituting (53)−(57) into (52),we have
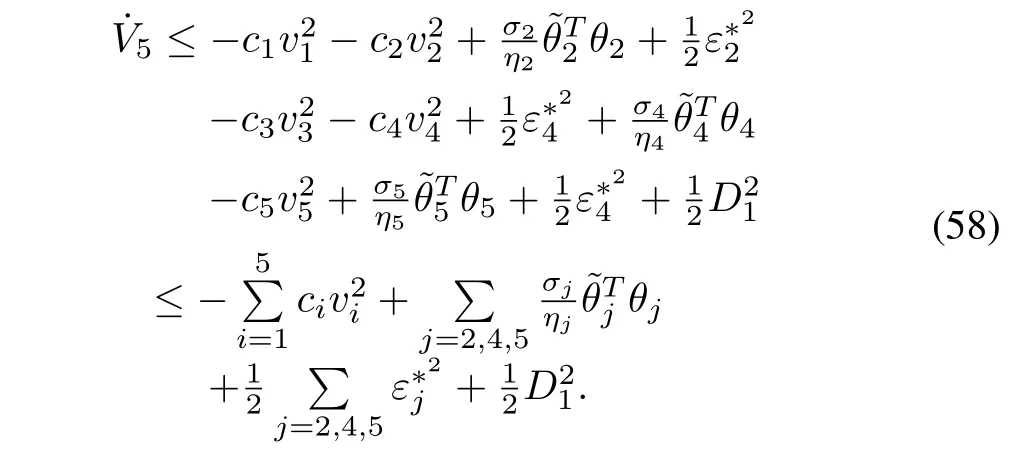
Then,(58) can be rew ritten as

Fig.2.Adaptive fuzzy backstepping control scheme.
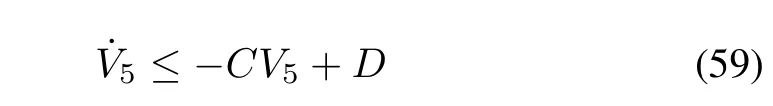
whereC=m in{2ci,2σj},i=1,...,5,j=2,4,5.
By integrating (59) over [0,t],we can get the solution of the above inequality
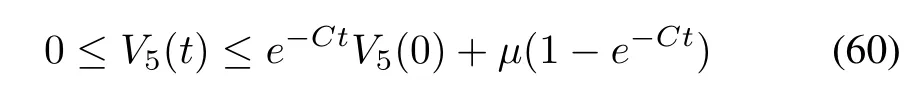
whereµ=D/C.
According to (60),it can be shown that all the signals in the closed-loop system are bounded.Meanwhile,we have:

Hence,according to (61),we conclude that the tracking error can be made small by increasing the values of design parametersci,σjor decreasingηjand (i= 1,...,5,j=2,4,5).
From above analysis and design,we can summarize the following Theorem.
Theorem 1.For the single-link flexible robotic manipulator system (1),the proposed adaptive fuzzy backstepping control design scheme can guarantee that the tracking errors converge to a small neighborhood of the origin and all variables in the closed-loop system are bounded.
The configuration of the aforementioned adaptive fuzzy control scheme is shown in Fig.2.
IV.SIMULATION
The parameters for the flexible robotic manipulator with the parameters[2]are given asJ1=J2= 40 kgm2,K t=10Nm/A,Kb= 0.976Nm/A,g= 9.8N/Kg,m= 0.102kg,F1=F2= 0.05Nm s/rad,R= 4.5 Ω,K= 30,L= 300H,N=1,d=0.4m.



Fig.3.The fuzzy rules.
Design the command filter as:

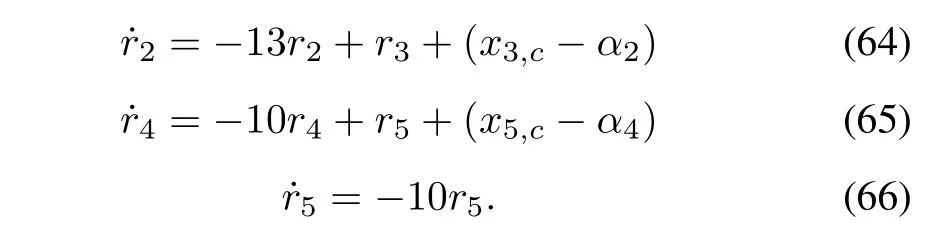
The virtual control functionαi,i=1,...,4,the controllervare chosen as follows:

The parameter adaptation laws,j=2,4,5 are chosen as follows:

The initial conditions of the states are chosen asx1(0) =0.03,x2(0) = 0.01 and the other initial values are chosen as zero.Choose the Butterworth low-pass filter asHL(s) =1/(s2+1.414s+1).
Simulation results in Figs.4−9 are obtained by the proposed scheme,where Fig.4 expresses the tracking trajectories of the output and the given reference signal.It is shown that under the actions of controller(55),the system output follows the desired reference signal well; Figs.5−6 show the statesxi,i= 1,...,5; Fig.7 shows the trajectory ofu(v); From Figs.4−7,it can be seen that boundedness ofxi,i=1,...,5,u(v) is verified.Furthermore,to demonstrate the adaptive learning performance,the norms of the system adaptive laws are demonstrated in Figs.8−10.
Remark 1:It should be mentioned that [11],[12]proposed different adaptive fuzzy control methods for a singlelink robotic manipulator system.However,[11],[12]did not consider the problem of actuator saturation.In addition,the references [11],[12]did not solve the so-called “explosion of complexity” problem which is caused by repeating differentiations of virtual control.In this paper,the problems of“explosion of complexity” and actuator saturation have been solved for the single-link robotic manipulator system.

Fig.4.The trajectories of y(solid) and yr(dashed).

Fig.5.The trajectories of xi,i=1,2,3.

Fig.6.The trajectories of xi,i=4,5.

Fig.7.The trajectory of u(v).

Fig.8.Norm of θ2.

Fig.9.Norm of θ4.
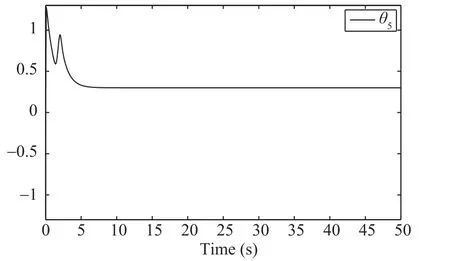
Fig.10.Norm of θ5.
To further demonstrate the effectiveness of the proposed control method,we apply the adaptive fuzzy tracking control scheme in [11]to the system (2).The simulation results are also depicted in Figs.11−12,where Fig.11 expresses the tracking trajectories of the output and the given reference signal,Fig.12 shows the trajectory ofu(v) .From Figs.11−12,it can be seen that the control method in [11]cannot obtain a better control performances,since there exists the actuator saturation.

Fig.11.The trajectories of y(solid) and yr(dashed).

Fig.12.The trajectory of u(v).
V.CONCLUSION
In this paper,an adaptive fuzzy backstepping control design method has been presented for a single-link robotic manipulator in the presence of actuator saturation.By combining the command filtered technique and FLSs,an effective adaptive fuzzy backstepping control approach is developed and the stability of the closed-loop system is proved.The main features of the proposed method are as follows.1)It solved the problem of actuator saturation by introducing the auxiliary design signal.2) By incorporating the command filter technique into the adaptive fuzzy backstepping design technique,the proposed control scheme solved the problem of ”explosion of complexity” inherent in the traditional backsteping control algorithms.Future research works will concentrate on the adaptive fuzzy output feedback control for the two-link flexible manipulator system on the basis of this study.
 IEEE/CAA Journal of Automatica Sinica2021年12期
IEEE/CAA Journal of Automatica Sinica2021年12期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Toward Coordination Control of Multiple Fish-Like Robots: Real-Time Vision-Based Pose Estimation and Tracking via Deep Neural Networks
- Exact Controllability and Exact Observability of Descriptor Infinite Dimensional Systems
- Energy Control of Plug-In Hybrid Electric Vehicles Using Model Predictive Control With Route Preview
- An Optimal Control Strategy for Multi-UAVs Target Tracking and Cooperative Competition
- Blockchain-Based Secured IPFS-Enable Event Storage Technique With Authentication Protocol in VANET
- Elastic Smart Contracts in Blockchains
