基于比例谐振控制的高速电机负载切换控制及稳定性分析

付贤政

(安徽国防科技职业学院 信息技术学院，安徽 六安 237011)

电机是依据电磁感应定律完成机械能与电能转换的一种电磁设备[1]。依据供电电源类型可以将电机划分为两大类，分别为直流电机与交流电机，而交流电机还可以划分为同步电机与异步电机。通过对比研究发现，永磁同步电机具备结构简单、可靠性高、转矩高、效率高、惯量比高的特征，应用范围日益增大，包含了工业、国防、航空等各个领域。尤其是近几年，风力发电新能源技术的兴起，促进了高速电机的进一步应用与发展[2]。

现代电机控制理论的飞速发展，高速电机硬件装置日渐成熟、完善，但是以软件形式存在的负载切换控制方法成了制约高速电机应用与发展的瓶颈。为此，研究高稳定性的高速电机负载切换控制方法，是现今电机控制领域重点研究问题之一[3]。在上述背景下，以提升高速电机负载切换控制方法稳定性为目标，深入分析负载下高速电机的运行特性，提出基于比例谐振控制的高速电机负载切换控制方法，并利用对比实验验证所提方法的有效性[4]。

1 高速电机负载切换控制方法研究

1.1 高速电机数学模型的搭建

为了分析高速电机负载切换控制方法的稳态运行性能，通过坐标转换，将三相交流绕组等效成两相直流绕组，呈现为旋转、垂直形式，使得变量部分解耦，以此为基础，构建高速电机数学模型，简化电机负载切换控制程序[5]。

电机负载切换控制需要的坐标系为静止坐标系与旋转坐标系。坐标转换即为三相静止坐标系ABC转换为两相静止坐标系αβ，再将其转换为两相旋转坐标系dq。前一过程称为Clarke转换，后一过程称为Park转换，具体坐标转换过程如下所示。

Clarke转换：为了简化运算过程，假设定子A相绕组与两相静止坐标系中的α轴重合，β轴在α轴逆时针90度的位置[6]。依据上述描述得到转换矩阵为

(1)

依据公式(1)将三相静止坐标系物理量转换为两相静止坐标系物理量，表达式为

(2)

式(2)中，f表示的是电流、电压或者磁链。

上述过程完成了静止坐标系三相到两相的转换，设置两相旋转坐标系d轴与转子磁极轴线重合，q轴在d轴逆时针90度的位置[7]。依据上述描述得到转换矩阵为

(3)

式(3)中，θ表示的是d轴与A相定子绕组的夹角。

依据公式(3)将两相静止坐标系物理量转换为两相旋转坐标系物理量，表达式为

(4)

将公式(2)与公式(4)有效的结合，得到三相静止坐标系物理量在旋转坐标系dq的表示为

(5)

三相静止坐标系、两相静止坐标系与两相旋转坐标系空间位置关系如图1所示。

图1 坐标系空间位置关系图

以两相旋转坐标系dq为基础，构建高速电机数学模型，其电磁转矩方程表示为

(6)

式(6)中，Tem表示的是电磁转矩；p表示的是参数；ψd、ψq分别表示的是定子d轴、q轴的磁链；iq、id分别表示的是定子q轴、d轴的电流；Lmd表示的是定子间d轴与q轴互感；if表示的是永磁体的等效励磁电流；Ld、Lq分别表示的是定子绕组d轴、q轴电感。

高速电机电压、磁链方程表示为

(7)

式(7)中，ud、uq分别表示的是定子d轴、q轴电压；ω表示的是谐振频率；R1表示的是阻力系数。

1.2 比例谐振控制器设计

传统高速电机负载切换控制采用的是PI控制器，具备较高的鲁棒性以及动态响应特征，但在交流电机中无法实现静差控制，为此设计比例谐振控制器[8-10]。

PI控制器经过PARK转化到两相静止坐标系下，即可得到比例谐振控制器[11-12]。在转换过程中，比例项保持恒定，则得到比例谐振控制器传递函数为

Gdq(s)=KI/s

(8)

式(8)中，Gdq(s)表示的是旋转坐标系下比例谐振控制器传递函数；KI表示的是比例系数；s表示的是相数。

将公式(8)转换为两相静止坐标系αβ，得到

(9)

式(9)中，Gαβ(s)表示的是两相静止坐标系下比例谐振控制器传递函数；Gdq1、Gdq2分别表示的是旋转坐标系下定子、转子传递函数；j表示的是负载机械折算的转动惯量[13-16]。

将公式(8)代入公式(9)得到谐振频率ω在旋转坐标系的旋转角速度，即为谐振项的正序、负序分量，通过叠加运算得到调节正负序分量的谐振项为

(10)

将公式(10)进行转换，从而得到理想比例谐振控制器传递函数为

(11)

式(11)中，GPR(s)表示的是理想比例谐振控制器传递函数；Kp表示的是积分系数；KR表示的是增益系数。

由公式(11)可以看出，在谐振频率ω处，增益无穷大，但是对其它频率信号无影响，这样能够对拥有谐振频率的正弦信号实现零稳态误差控制[17-21]。

1.3 高速电机负载切换控制

依据上述设计的比例谐振控制器(目标电机实物图见图2)，制定高速电机负载切换控制框架，具体如图3所示。

图2 目标电机实物图

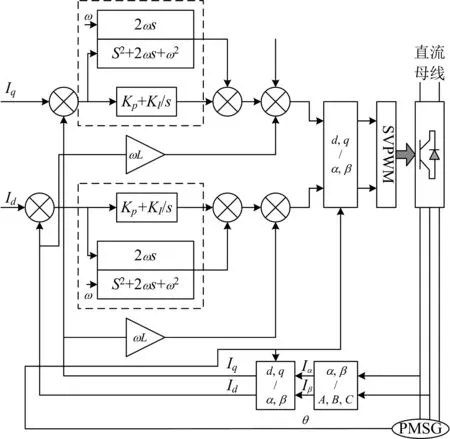
图3 高速电机负载切换控制框架

如图3所示，当电流中的直流分量经比例谐振控制器时存在：

式(12)中，上角标*表示的是控制变量；下角标1表示的是直流分量输出结果，kpl、kIl分别表示的是PI中的积分系数与比例系数。

共模分量经比例谐振控制器时存在

(13)

式(13)中，下角标2表示的是共模分量的输出结果。

将公式(12)与公式(3)进行叠加处理，得到比例谐振控制器指令电压表示为

(14)

通过公式(14)可以看出，利用比例谐振控制器可以使频率为ω的正弦信号实现稳定性的负载切换。

1.4 零稳态误差控制实现

通过比例谐振控制器传递函数可以发现，其与低通滤波器原理是相同的，只对谐振频率的信号有作用，对其他频率信号具有衰减作用。

高速电机负载切换控制的传递函数表示为

(15)

式(15)中，IL表示的是电机负载切换控制传递函数；K表示的是控制系数；G(s)表示的是比例谐振控制器频率为ω的增益；Z表示的是离散因子；Iref表示的是增益约等值；ψf表示的是永磁体产生的磁链。

将公式(15)利用双线性变换方法变换，得到离散化的传递函数为

(16)

式(16)中，Gi(z)表示的是离散化的传递函数；b0、b1、b2、a1与a2均为离散参数。

通过整理得到比例谐振控制器差分方程为

(17)

综上所述，基于比例谐振控制器实现了高速电机负载切换的稳态控制，控制程序较为简单，为高速电机的应用提供了有效的支撑。

2 水冷高速永磁体同步电机负载切换控制稳定性分析

对于高速电机来说，负载切换控制稳定性决定着高速电机的应用效果，为此，设计仿真对比测试验证设计方法的稳定性，具体测试过程如下所示。

2.1 测试准备

为了保障测试的顺利进行，选取水冷高速永磁体同步电机作为测试对象(电机转轴实物图见图4)，其电极由2极表贴的，缠绕在碳纤维护套上，定子规格为24槽，电机应用于挂叶轮的制冷设备上。

图4 电机转轴

测试环境参数设置情况如表1所示。

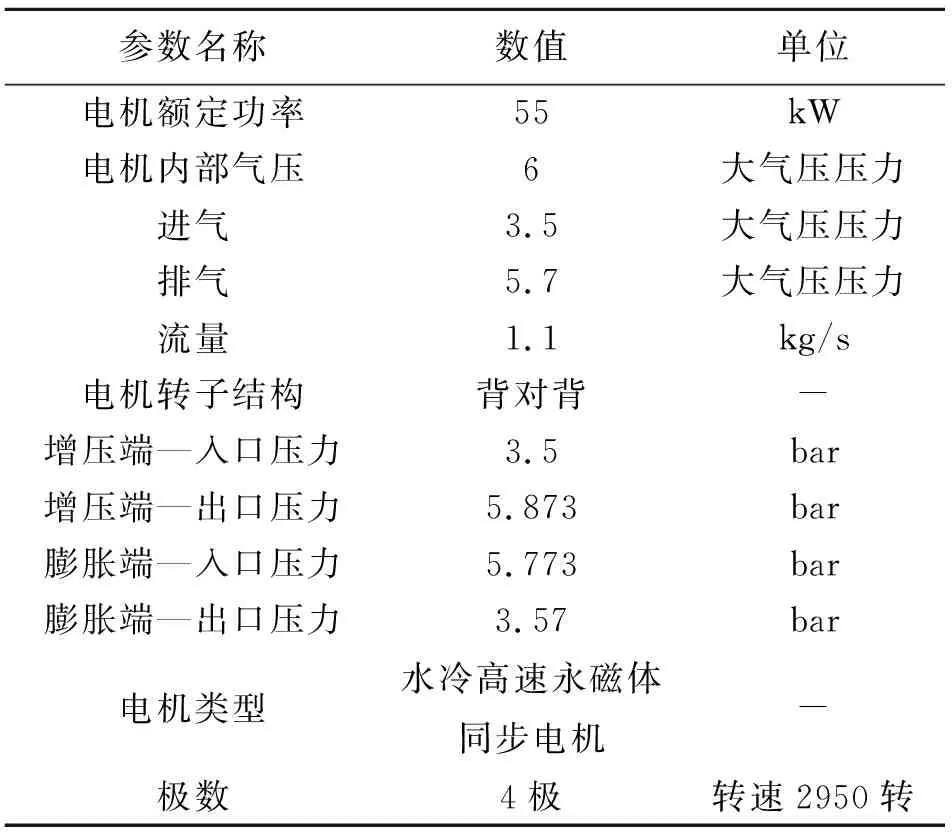
表1 测试环境参数表

比例谐振控制器传递函数中的增益系数与截止频率影响着谐波抑制效果，为此，利用伯德图确定最佳增益系数与截止频率。

比例谐振控制器增益系数与截止频率变化曲线如图5所示。

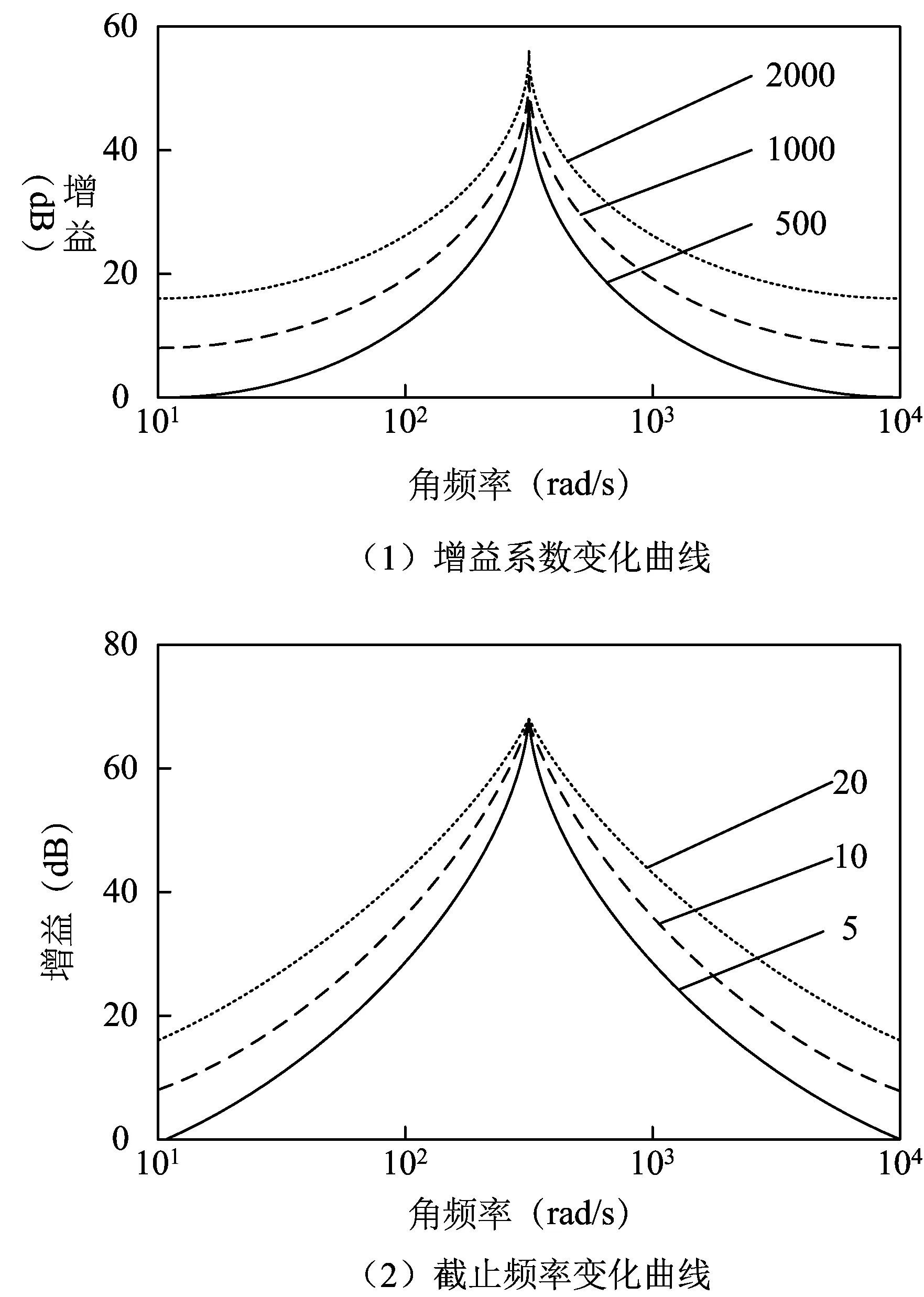
图5 比例谐振控制器增益系数、截止频率变化曲线图

如图5所示，当增益系数KR为2000，截止频率ωc为10时，谐波抑制效果最佳。

2.2 稳定性测试分析

采用Matlab/Simulink工具箱，根据获得的最佳增益系数与截止频率设置比例谐振控制器，利用基于ATS的控制方法、基于无传感器的控制方法以及基于比例谐振控制的控制方法对水冷高速永磁体同步电机负载切换进行控制测试，测试结果如下所示。

2.2.1 电机转速追踪

采用基于ATS的控制方法、基于无传感器的控制方法以及基于比例谐振控制的控制方法对电机实时转速进行追踪，并与电机实际转速追踪进行对比，测试得到高速电机转速追踪结果如图6所示。

图6 高速电机转速追踪结果

分析图6可知，当运行时间为10 min时，实际转速为1200 r/min，ATS控制方法的追踪转速为1200 r/min，无传感器控制方法的追踪转速为2900 r/min，比例谐振控制方法的追踪转速为1200 r/min。当时间增加到30min时，实际转速为1200 r/min，ATS控制方法的追踪转速为1880 r/min，无传感器控制方法的追踪转速为2600 r/min，比例谐振控制方法的追踪转速为1260 r/min。本文方法的追踪转速始终与实际转速相差不大。分析整体可知，本文方法追踪的转速与实际转速曲线基本重合，证明本文方法转速追踪效果较好。

2.2.2 高速电机转矩

为了进一步验证本文方法的控制效果，利用上述方法验证高速电机转矩的控制效果，得到结果如图7所示。

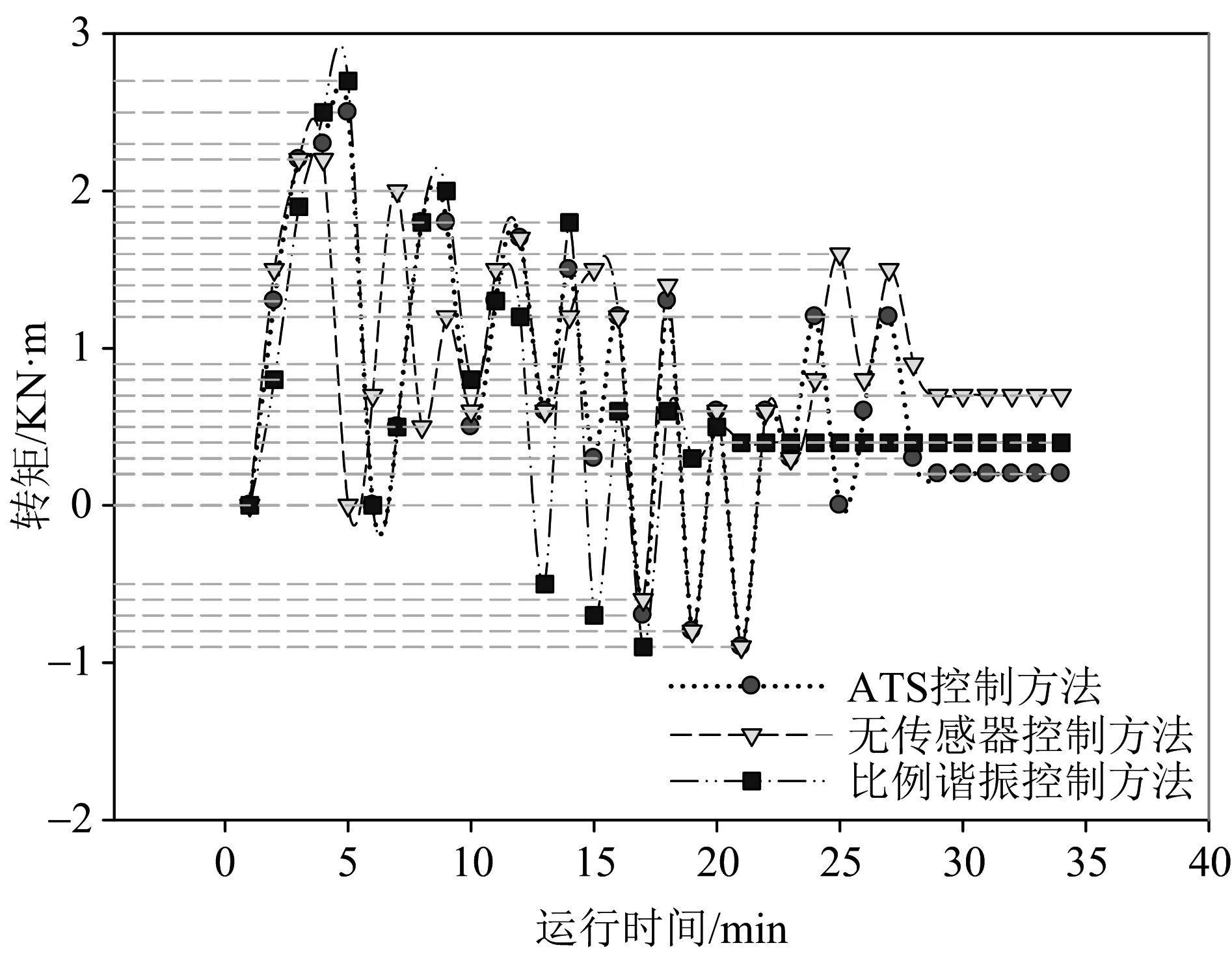
图7 高速电机转矩

分析图7可知，不同方法下高速电机转矩控制效果不同。当运行时间为10 ms时，ATS控制方法的转矩为0.5 KN·m，无传感器控制方法的转矩为0.6 KN·m，比例谐振控制方法的转矩为0.8 KN·m。当运行时间为10 ms时，ATS控制方法的转矩为0.5 KN·m，无传感器控制方法的转矩为0..6 KN·m，比例谐振控制方法的转矩为0.8 KN·m。当运行时间为22 ms时，比例谐振控制方法的转矩为0.4 KN·m。此时本文方法已经处于转矩平衡状态。ATS控制方法、无传感器控制方法达到平衡的时间分别为29 ms与28 ms，相比其他方法，本文方法达到平衡的时间比较快。

2.2.3 高速电机负载稳定性

为了验证本文方法的高速电机负载稳定性控制效果，采用基于ATS的控制方法、基于无传感器的控制方法以及基于比例谐振控制的控制方法验证高速电机负载稳定性，得到结果如表下所示。高速电机负载稳定性数值为暂态负载功率与电机负载功率的比值。

由表2中数据可知，当迭代次数为60次时，ATS控制方法的电机负载稳定性为80%，无传感器控制方法的电机负载稳定性为72%，比例谐振控制方法的电机负载稳定性为92%。当迭代次数增加到210次时，ATS控制方法的电机负载稳定性为78%，无传感器控制方法的电机负载稳定性为75%，比例谐振控制方法的电机负载稳定性为98%。本文方法一直具有较高稳定性，这是因为本文方法利用坐标转换，将三相交流绕组等效成两相直流绕组，使得变量部分解耦，并通过高速电机数学模型设计比例谐振控制器，提升了电机负载稳定性控制效果。

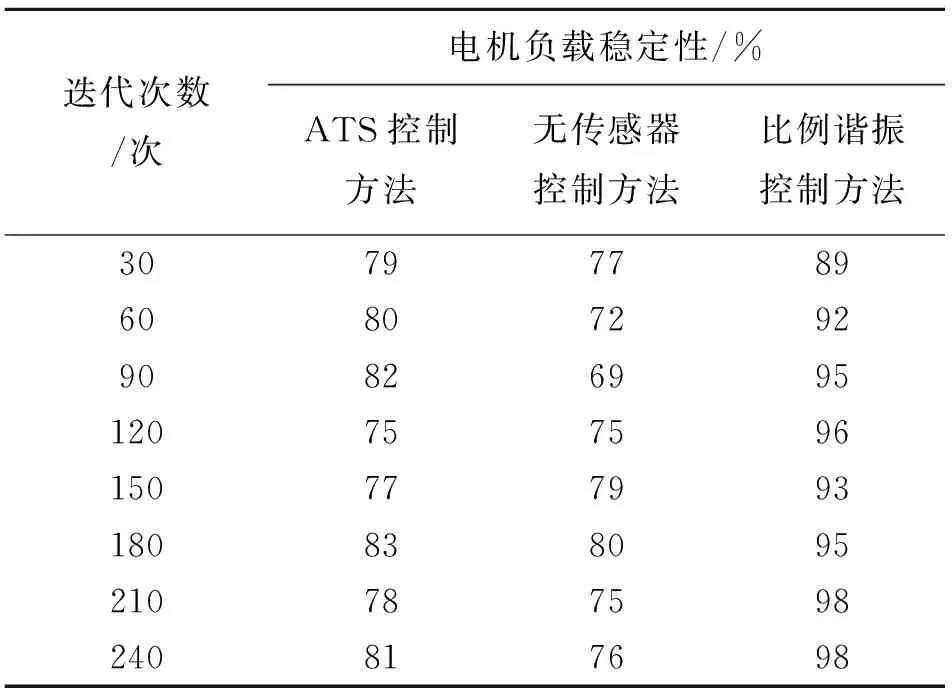
表2 不同方法的高速电机负载稳定性

3 结论

为解决高速电机负载切换稳定性不佳问题，本文通过构建高速电机数学模型，设计比例谐振控制器，确定控制器传递函数，获得电机负载切换稳定控制差分方程。通过实验得出以下结论：

(1)本文方法追踪的转速与实际转速曲线基本重合，证明本文方法转速追踪效果较好。

(2)相比ATS控制方法、无传感器控制方法，本文方法达到平衡的时间比较短，当运行时间为22 ms时，比例谐振控制方法的高速电机已经达到平衡状态。

(3)本文方法一直具有较高稳定性，当迭代次数增加到210次时，比例谐振控制方法的电机负载稳定性为98%。