海上船舶污染事故应急资源调度研究
薛栋梁



摘 要:针对海上船舶污染事故的特殊性,以一次性消耗系统为研究,结合海事局在应急资源调度方面的重要意义,基于理想点法提出一种具有实践意义的应急资源调度模型。
关键词:海上突发事故;一次性消耗;资源调度;理想点法
中图分类号:U292.4 文献标识码:A
0 引言
近年来,海洋经济活动日益频繁,海上船舶来往增多,海上通航密度增大,使得海上船舶污染事故发生的风险也越来越大。倘若突发海上船舶污染事故,可能危害人命、造成损失财产和破坏生态环境,因此需要强化海上船舶污染事故应急管理工作。而应急资源调度是事故应急中至关重要的一环,海上船舶污染事故的应急能力的實现在很大程度上取决于应急资源的积极调度。鉴于海上船舶污染事故应急资源调度的时效性和经济性,本文主要研究解决如何在满足资源需求的条件下,完成资源的最优调度,以保证实现应急开始时间最早、参与调度的供应点最少和资源调度成本最低的目标。
1 问题描述
在海上突发船舶污染事故后,往往需要多种应急资源的参与调度。另外由于应急资源大都储备在岸基应急资源供应点,单个供应点往往不能满足应急需要,这就要求考虑多个供应点协同响应。海事局作为船舶污染事故应急主导地位,不仅要考虑事故的应急效率和应急费用,还应当考虑参与调度工作的供应点尽可能的少。为此,本文考虑在单一供应点可能无法满足事故点需求时,如何在若干个供应点中选取参与应急调度的供应点以及各自所要调度的应急资源种类及数量,最终给出一个最优的调度方案。
2 应急资源调度模型
2.1 模型建立
假设某个海域发生船舶污染事故,该海域内有n个应急资源供应点,记为Ai(1≤i≤n),有应急点Bp(1≤p≤s)需要供应m(m>1)种应急资源Xj(1≤j≤m),其中第j种应急资源的需求量为xpj,供应点Ai中存储第j种资源的存储量为xij(xij≥0,且xij不全为0)。从供应点Ai到应急点Bp的运输时间为tip(tip>0),为不失一般性,假定t11≤t21≤…≤tn1≤t12≤t22≤…≤tns。
记调度方案为:
其中表示对于第p个应急点的第j种资源的应急调度方案;a1,a2,…,ak为数列1,2,…,n的一个子列;,,…,表示从n个供应点中挑选出k个供应点a1,a2,…,ak为第p个应急点实际提供第j中资源的供应量,且。记所有方案的集合为。
定义方案中参与调度的供应点个数为;应急开始时间为,表示该调度方案应急资源全部到位时间,即(tip),i=a1,a2,…,ak,。根据“应急时间最早”、“供应点最少”的目标,构建海上船舶污染事故应急资源调度模型如下:
(1)
该模型的约束条件为:
(2)
(3)
其中条件(2)表示供应点Ai不全为空存储,有参与资源调度的前提条件;条件(3)表示应急资源供应量应满足需求量,同时不超过总存储量。
为方便模型求解,作如下假设:
①该应急资源调度系统为一次性消耗系统,即应急点所需全部资源都到达时才能进行应急活动;②整个调度过程为一次性需求,即不会发生新的需求,且不考虑往返调度;③各个应急资源供应点的各类资源量及应急点所需的各类资源量已知,不同类型的应急资源可用同一应急船舶运输;④存在单个供应点无法满足整个事故需求的情况,但整个应急资源供应点存储满足需求;⑤应急点及各个应急资源供应点的地理坐标已知,即应急点与供应点之间距离已知;应急船舶平均航速已知且恒定,则可将各个应急资源供应点到应急点之间的运输时间看成是已知量(运输时间=距离/船速)。
2.2 模型求解
采用理想点法对模型进行求解,基本思想是求出各目标函数的最优解和最劣解,即其正负理想点,利用公式求出各非劣方案与最优最劣值(正负理想点)的相对接近度,按相对接近度的大小排序,其值最大的方案即为最优方案[1-2] 。据此可将多目标模型(1)转化为单目标模型(4)和模型(5):
(4)
(5)
下面需要分别求解(4)和(5)的最优解和最劣解。不妨设、、、分别为(4)和(5)中的正理想点和负理想点[3],构造任一给定调度方案与正负理想点的距离和:
(6)
(7)
其中、分别为关于应急开始时间和参与调度的供应点个数的权重,满足归一化条件=1,其取值可以根据具体问题来确定取得。本文中,由于应急开始时间较于参与调度的供应点个数更加重要,本文取=0.7,=0.3。
方案与理想点的贴近度:
(8)
将所有可行方案对于理想点的贴近度按由小到大的顺序排列,值越大,对应的方案越优,对应最大值的方案即为最优方案。
本文研究的是一次性消耗系统,对于每个应急点Bp分别求出每一种应急资源的应急开始时间,并从中找出最大值即为该应急点Bp的应急开始时间,所有应急点的应急开始时间最长的即为。假设所有参与资源调度的供应点到应急点的运输时间的最大值为tmax,则对任一方案,其应急开始时间必定在和tmax之间,因此可得到即为tmax。
定义a1,a2,…,ak为数列1,2,…,n的一个子列,如果存在序列,…,,使得(为应急点Bp所需第j种应急资源的量),则称k为序列对的临界下标,即应急点Bp所需第j种应急资源的最少供应点个数。据此可求出每一种应急资源的临界下标,然后找出最大临界下标记为。由于是考虑到应急时间最早,所有不一定与相等,每一个应急点对应的供应点的组合也不一定相同。在情况下若每个应急点所对应的应急开始时间相同,且参与资源调度的供应点的组合也相同,则;反之,令,继续按照上述方式进行寻找,直到找到,且对于任一调度方案满足,则。
通过上述方式求解、、、,利用公式(6)、(7)、(8)计算所有,取得最大值的方案即为最优方案。
3 算例验证
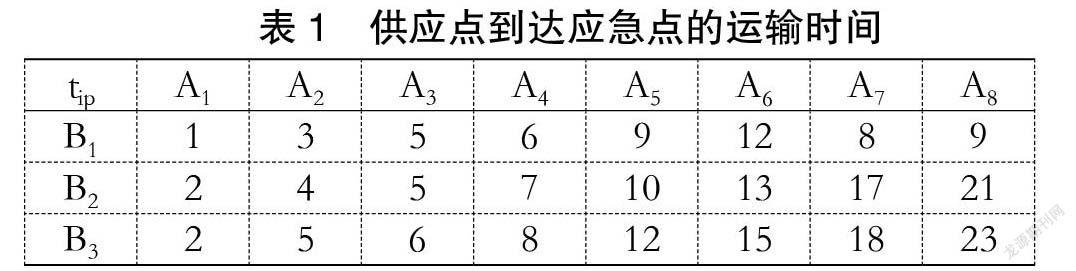
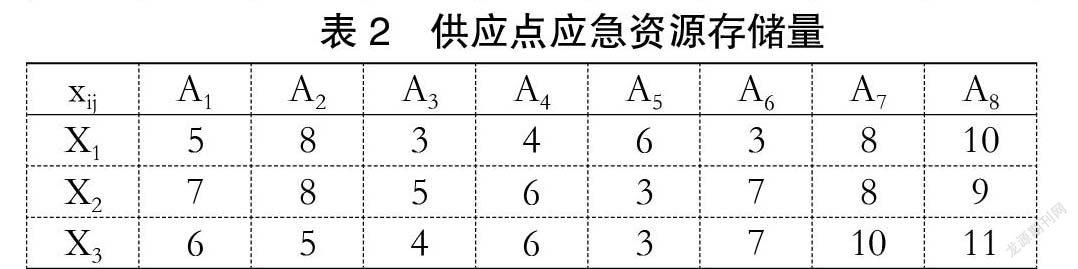
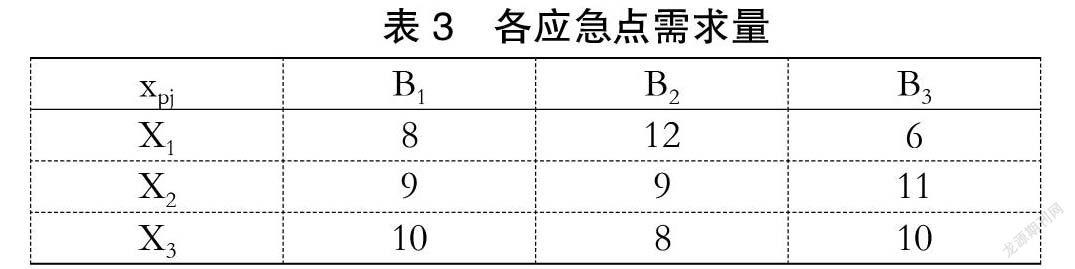
假设某一海域突发船舶污染事故,在事故海域有3个应急点,有8个应急资源供应点,每个供应点存储不同量的3种应急资源,具体信息如表1、表2和表3所示:
比较各个值,经计算得到其中最大值0.569,与此对应的最佳资源调度方案为A1、A2、A3、 A4 、A5、 A6共6个供应点,应急开始时间为15。
4 结语
海上船舶污染事故的应急资源调度问题是海上应急管理中的重要内容,也是海事相关工作人员深入探究的重要课题。本文建立了适用于海上船舶污染事故应急资源的调度模型,并利用理想点法完成了对模型的求解。通过算例验证表明,该方法实用简便,能够更好地在实际应用中解决针对海上船舶污染事故的多资源调度问题。值得一提的是,利用理想点法求解本模型的解是近似最优解,而非理想解,因此后期需要对此进一步加深研究。
参考文献:
[1]赵雪峰,李金林.110报警平台的警力资源调度优化[J].北京理工大学学报,2014(2):88-91.
[2]罗吴辉,栾翠菊.溢油应急决策中的物资调度方法[J].计算机系统应用,2014(10):142-146.
[3]宋琦.铁路突发事件应急资源调度问题研究[D].成都:西南交通大学,2011.

