筏板基础抗浮桩性能及对基础受力影响探讨

黄伟杰

（福建立盛建筑集团有限公司， 福建 漳州 363000）

1 筏板基础抗浮桩施工现状

在我国城市化建设中，随着城市化建设的不断发展，地下建筑空间得到了开发利用。因此，超大超深地下结构不断增多，但带来的抗浮问题也愈加突出。目前，在其滨海、地下水位等地区，需要采取合理有效的施工方案，完成全新技术的融合应用。我国以往在建筑中，针对于建筑物基础的抗浮设计，大多采用灌孔桩柱桩等方法，将灌孔桩与柱子连接，导致灌孔桩间距较大。因此，需要较厚底板才可以抵抗其地下水浮力产生的弯矩剪力，但很容易导致底板厚、造价高、经济效益不足[1]。

近年来，在抗浮性中，抗浮桩以性能良好、施工方便的优势，得到了广大地下工程施工者的信赖。有关抗浮桩的荷载传递机能以及计算方法也得到了优化。我国目前施工技术虽然尚在发展中，与发达国家相比有一定差距，但相关的理论研究基础正在不断更新、优化中，且由于抗浮桩实验周期长、成本高，因此需要使用工程量判定市场实践模式，以分析抗浮桩的承载力，并分析其抗拔桩极限承载力的确定方法，对于影响抗浮桩承载力因素以及提高其承载力的方案进行研究。为了全面提升目前抗浮桩的应用前景，对于筏板基础抗浮桩力学性能的研究非常迫切并具有实际意义。在后续改进中，可以结合大量的文献资料，分析其理论方法以及作用，对其用有限元分析方法进行研究[2]。

2 基本工程概况分析

为了能够更好的便于施工，因此需要对本文的漳州客运南站建设项目（一期）-客运站房基本工程概况进行分析。在本文的概况中，整个地下水对于结构具有轻微腐蚀性和抗浮（拔）桩的受力，因此需要保障其整个结构能够避免地下水的侵蚀和影响，通过筏板，可以对接触水部分的钢筋能够起到有效的保护效果（如图1 所示）和抗浮（拔）桩的做法（如图2 所示）。

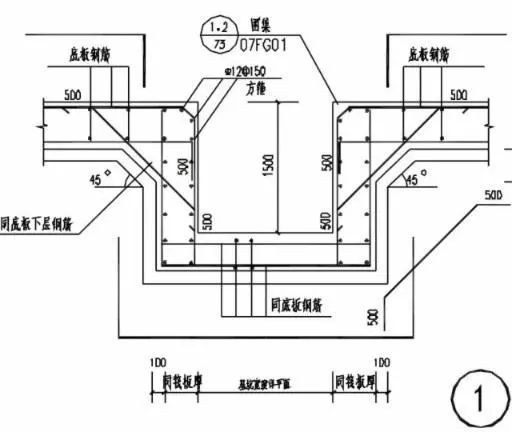
图1 筏板基础平面图

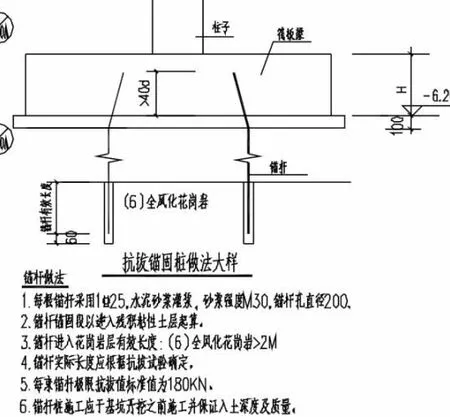
图2 筏板基础平面图

3 抗浮单桩抗浮极限承载力影响因素分析

在目前的抗浮桩承载性能研究中，我国对此认知较不明确。在工程中，有关抗浮桩的使用，大多数凭借其以往的工程经验进行施工。但根据整个工程施工模式，可以得知影响抗浮桩性能的制约因素较多。包含桩长、桩身、成桩方式、桩身材料、性能等，因此在后续表现中，除对桩体自身进行改进外，也需要融合计算因素。例如，根据ANSYAS 建立抗浮单桩计算模型，以便对浮力作用下的抗浮桩性能进行分析研究。

3.1 ANSYAS 模型建设分析

在本论文中，采用ANSYAS 计算模型，根据整个桩体，采用圆柱实体，其长度以及直径可以根据其考虑模式选择不同的建设方案。将桩土之间作为无厚度接触，并在后续模拟过程中，将其土体视作无限的空间体。合理选取计算边界，消除边界自身的影响作用。根据其试算，在本章节中可以根据水平方向的土体，将尺寸规定为12 倍。将其竖直方向为三倍中长土体的初始应力。通过施加Z 速度方案进行建立，完成初始应力场的建设。并根据土体侧向结构，施加共同作用，根据床桩身的材料变形比例，考虑桩体之间的共同作用。在模拟过程中，将抗浮桩作为弹性材料。例如，针对土体可以采用摩尔库伦模型进行处理。根据最大应力以屈服准则为理论基础，考虑最大剪力应准则，且土体在发生破坏前，对其采用弹性模型。

3.2 模型建设材料屈服准则

在对混凝土以及承载土体进行有限元分析中，其可以设定以下的假定点。例如，假定桩体混凝土为理想材料，因此不考虑材料自身出现的屈服以及破坏。且根据主体材料的弹塑性，以Drucker-prager 为准则，考虑自重影响以及侧压作用。

4 抗浮设防水位的确定以及浮力的计算流程

在地下水的研究中，我国已然取得一定的研究成果。但目前对于整个抗浮措施的研究缺少系统理论成果。在抗浮桩设计过程中，需要明确计算公式：

如以下计算公式F=ym·hz

在整个公式中，“hz”可以将其判断为地下水浮力高差，通过该公式，可以得知地下水浮力为一定的不确定性。而“hz”的职责，便是确定整个水浮力值的大小。因此，在设计过程中，需要确保整个地下室水位的标高，以保障地下水的浮力以及水位能够根据水文地质以及岩土工程地质等各方面条件，实现地下水浮力的计算。在整个水压力值以及基底的地下水浮力中，通过大量的实践资料，可以保障地下水压力值以某种现行方式增加。因此，地下水位的变化，将导致地下水压力值不断变化。要想确保在最大地下浮力能够存在明显的参考性因素，就需要对现行标准提供合理有效的规范。

4.1 抗浮桩分担净浮力计算

在计算过程中，通过整个建筑的荷载路径，可以由相关的剪力墙将荷载传递到基础桩上。随后，通过基础桩传递至地基。在整个传输过程中，可以将抗浮桩布置在剪力墙下面，保障抗浮桩的结构自重以及其他抗浮桩之间的自重。在实际工程中，采用厚度较大的筏板，以根据不同位置的抗浮桩，完成由上而下的荷载力度设置，如以下公式：F=（yw·hz-G）A。

根据公式，可以得知“yw”为水的自身重量，“hz”则包含地下水浮力高差，而“A”则代表抗浮桩分担面积，“G”则是单位面积上的自重[3]。且由于整个抗浮桩所承担的建筑自重各不相同，根据计算公式，得出整个水的静浮力也不同。

4.2 抗浮桩侧摩擦力阻计算

根据不同的地下水土层结构，可以得知地下土层存在一定的差异性。对于整个抗浮桩设计而言，其土自身差异性将会导致抗浮桩摩擦力阻不同。在设计过程中，将土体侧摩擦力设定为均匀，在抗浮桩与土体之间，通过此种假定条件，可以对抗拔力进行计算。在假定过程中，实际工程不存在相关情况。但在研究过程中，如忽略此摩擦力的设置，将会导致差别较大。因此，可以推断出整个抗浮桩的摩擦力分布。在研究成果中，对抗浮桩以何种形式、何种摩擦力分配，需要进行明确说明。

5 建立抗浮单桩有限元模型

5.1 有限元模型的选取

在选择过程中，通过三维有限元模型，可以进行模拟以及划分。在设计过程中，需要根据桩以及土之间的相互作用，以分析二者之间的相对位是否具有密切关联。在设置过程中，根据“solid95”完成三维8 节点的高阶版本设置，可以适应不同规则的形状，且可以避免精细度的损失[4]。在建设过程中，每个节点包含三个自由度，由x、y、z 方向进行位移。通过整个目标面形状，描述相关模型的边界过程，可以根据抗浮桩的目标段单元进行设置，附加平移或旋转位移，以应对整个抗浮桩目标单元施加力矩。在设置过程中，需要考虑到桩土之间的相互作用，保证单元可以在桩土之间建立耦合技术。分析在覆盖过程中，可以根据表面的不同形状，当外合作用在桩土之上时，其接触将会产生[5]。

5.2 土体结构模型分析

经相关资料进行查阅，可以得知在建设过程中，计算模型可以分析整个土体的变形面积[6]。分为线型、非线型以及弹塑性，由于各层土质分布较为均匀，因此土体的物理性能较好，可以在土体以及结构之间存在较小的相互作用。如土体的变形较为均匀，则可以通过线型计算模型，如整个土体的应力变化较大，出现非线性变形，则可以选用非线性弹性模型或函数型模型。在模型选择中，可以根据具体情况进行设置。在建设过程中，塑形理论模型可以很好弥补目前非线性模型存在的缺陷。且随着整个科研技术的不断进步，弹塑性模型弥补了非线性模型的不足。可以很好地反映土体在大应力作用下，产生的应变以及变形，也可以描述以及反映土体在卸载后的变形情况。根据整个弹塑性理论，确定模型的计算依据，以保证在岩土工程中能够得到明显且有效的应用[7-8]。在模型设置中，可以通过以下两个公式进行设置：“eij=eij+eij‘p’”、“deij=deij+deij‘p’”。

6 结束语

综上所述，在阀板基础抗浮桩性能以及其基础受力影响分析中，可以通过建设相关模型得知整个桩体自身的受力模式。以便根据模型的建设结果，得出合理有效的改进措施，分析整个影响规律。在筏板基础桩中，性能以及其基础梳理影响通过模拟，发现筏板可以使抗浮桩相对位移以及内力得到调整，使整个荷载结构的传递性能实现优化。