基于负刚度磁弹簧的超低频振动速度传感器的设计与性能分析

周振华，傅逸轩，杜荣华

(1.长沙理工大学汽车与机械工程学院，湖南长沙 410114;2.机械装备高性能智能制造关键技术湖南省重点实验室，湖南长沙 410114;3.工程车辆轻量化与可靠性技术湖南省高校重点实验室，湖南长沙 410114 )

0 引言

在超精密减振、桥梁检测和地震学等领域中，对于超低频振动信号的检测一直受到高度重视[1]。如何有效地检测到超低频振动信号已成为了超精密减振技术的核心之一，例如天棚阻尼隔振控制方法需要精确地检测振动速度信号以进行反馈控制[2]，同时在地质勘探和地震学中，精确地检测到超低频振动信号有利于扫描地质结构[3]。目前超低频振动信号的检测主要采用磁电式速度传感器，由于其频响特性为典型的高通特性，同时受其机械结构刚度和共振质量、体积的制约，无法实现对超低频振动信号的检测[4]，因此如何降低速度传感器的下限测量频率是关键。

近年来，由于负刚度能够降低系统刚度，因此在低频超低频减振领域中得到了广泛的应用。李爽等提出双环永磁体负刚度结构，以降低隔振器的固有频率[11]。N. Zhou等设计一种永磁体和电磁铁组成可调负刚度结构，用于被动和半主动隔振[12]。高双等开发一种欧拉屈服梁负刚度结构的隔振器，分析了激励幅值、阻尼等参数对系统传递率的影响[13]。刘兴天等提出一种欧拉屈服梁负刚度结构的隔振器，分析了激励幅值和载荷对隔振器性能影响[14]。A. Carrella通过一对斜弹簧设计了负刚度结构，主要讨论了负刚度隔振器的非线性特性[15]。然而现有的负刚度结构在工作点附近表现出强烈非线性特性[16]。何剑锋等运用4个水平弹簧设计一种准零刚度绝对位移传感器，并运用在Stewart微动隔振平台上[17]。负刚度一方面能够降低结构整体刚度，但另一方面也引入非线性项[18]。显然，运用现有的负刚度机构来降低速度传感器的下限频率会导致传感器响应出现非线性动力学响应特性，无法满足精确测量的要求。显然，为了降低传感器测量下限，满足测量要求，负刚度元件在工作点附近需要拥有线性负刚度特性，并且其负刚度值能与正刚度元件匹配。

因此，为了实现速度传感器的低频扩展，结合速度传感器低频扩展对线性负刚度特性的要求，本文提出一种基于负刚度磁弹簧的超低频速度传感器，通过等效磁荷法建立负刚度磁弹簧的磁力与刚度模型，分析了负刚度磁弹簧的几何参数对其负刚度特性影响规律；并进一步通过数值方法分析了所提出的速度传感器的频响特性。

1 传感器的结构与参数

超低频速度传感器的结构如图1所示，由测量系统和振动系统构成，测量系统由测量磁环和线圈组成；振动系统由负刚度磁弹簧、正刚度弹簧和片簧组成。负刚度磁弹簧由双环永磁体PM1和双环永磁体PM2并联组成，而PM1和PM2都由内磁环和外磁环同轴配置构成，并且PM1和PM2之间保持等距离安装，保证PM1和PM2的磁场互不干扰。PM1和PM2的内磁环都固定安装在中心杆上，外磁环固定安装在外壳上。负刚度磁弹簧提供负刚度；正刚度弹簧一端连接中心杆底部，一端连接外壳，并为系统提供正刚度；片簧约束中心杆沿着Z轴方向振动。当中心杆沿轴向振动时，测量磁环与永磁体会产生相对运动，线圈切割磁感线产生感应电动势，将线圈和磁环的相对运动速度信号转换为与速度成比例的电压信号，从而实现速度信号测量。

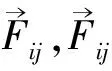
h11′=za+b-h
h12′=za+b+h
h21′=za-b-h
h22′=za-b+h

(1)

永磁体磁极化强度为

(2)

2 负刚度特性建模

根据等效磁荷法，内磁环与外磁环之间的轴向磁力为内外磁环4个表面1、2、1′、2′上磁荷的相互作用力叠加而成[19]，因此轴向磁力FZ为

FZ=F12′+F21′-F11′-F22′

(3)

根据式(1)和式(2)，将在内磁环表面i和外磁环表面j之间的轴向磁力可以定义为

r1r2dr1dr2dθ1dθ2

(4)

其中a(hij)为

(5)

式中：J1为外磁环提供的表面磁极密度；J2为内磁环提供表面磁极密度。

通过式(4)，对内磁环和外磁环之间的相对距离za进行求导，内外磁环之间刚度Kz为

(6)

基于文献[20]，永磁体刚度为

(7)

f=f(h11′)-f(h21′)+f(h22′)-f(h12′)

(8)

其中

(9)

因此，负刚度磁弹簧刚度Km表达式为

(10)

式中：Kz1为双环永磁体PM1的刚度；Kz2为双环永磁体PM2的刚度。

在平衡位置附近，永磁体之间的磁力和刚度分别使用三次多项式和二次多项式近似拟合[16]：

(11)

(12)

式中：p为常数项系数；k为二次项系数。

p用于表示负刚度的强度或线性分量，k用于表示负刚度的非线性分量。因此，负刚度磁弹簧的刚度表示为

(13)

(14)

为了定量描述负刚度磁弹簧的非线性度，定义负刚度磁弹簧的刚度与线性分量的最大偏差和线性分量的百分比为非线性度δ，则δ表示为：

(15)

3 永磁体参数对负刚度特性的影响规律

基于速度传感器要求的线性负刚度幅值和期望的线性负刚度位移区间，因此，首先确定线性负刚度的位移区间为za=±5 mm，进一步分析轴向高度差、气隙宽度和气隙位置等参数对负刚度磁弹簧负刚度特性的影响规律。其中，负刚度磁弹簧的几何参数如表1所示。

表1 负刚度磁弹簧的几何参数

3.1 轴向高度差对负刚度特性的影响规律

结合式(14)可知，当非线性分量k1+k2足够小时，负刚度磁弹簧的刚度非线性分量可以忽略。同时，负刚度磁弹簧结构中的单个双环永磁体的轴向高度差会影响非线性分量的正负取值[16]。因此，通过高度差φc和高度差φv的调整可以使得非线性分量k1+k2足够小，从而实现线性负刚度特性。当高度差的取值范围为φ=6～20 mm时，以非线性分量最小为目标的高度差φc和高度差φv的匹配规律如图2(a)所示，其拟合方程为

φv=10.114 96(φc-8.923 45)-0.102 16

(16)

根据式(16)可知，随着双环永磁体PM1高度差φc的增大，所匹配到的双环永磁体PM2高度差φv反而减小。基于以上高度差匹配规律，所得到的匹配负刚度磁弹簧的负刚度幅值和非线性度如图2(b)所示，随着高度差φc增大，负刚度幅值增大，非线性度相应增强；当高度差φc为10 mm时，负刚度幅值出现峰值，同时非线性达到最大；进一步增大高度差，负刚度幅值减小，非线性度相应减弱。结果表明：对于不同高度差匹配下的负刚度磁弹簧，其负刚度呈现出了不同特性，因此可以通过调整负刚度磁弹簧的高度差φc来匹配的高度差φv，并获得所需要负刚度幅值和非线性度。

3.2 气隙宽度对负刚度特性的影响规律

当气隙宽度d的取值范围为2～10 mm，负刚度特性随着气隙宽度的变化规律如图3所示。从图3(a)中可知，不同气隙宽度下，匹配曲线变化趋势相同，但随着气隙宽度增加，匹配曲线向右上方偏移，匹配区间相应增大。进一步研究不同气隙宽度下负刚度磁弹簧的负刚度特性的变化规律，具体结果如图3(b)和图3(c)所示。由图3(b)和图3(c)可知，气隙宽度对负刚度幅值和非线性度影响较大，非线性度整体随着气隙宽度增加而减弱，但负刚度幅值整体减小；同时，气隙宽度增大还会使负刚度幅值和非线性度的峰值减弱，曲线更为平缓。基于以上分析，为了获得负刚度磁弹簧的线性刚度特性，可以通过增加气隙宽度来实现，但增加气隙宽度又会导致负刚度幅值减小。因此在设计中需要综合两者考虑，在保证负刚度磁弹簧的负刚度值大小同时尽可能具有较小的非线性。

3.3 气隙位置对负刚度磁弹簧的影响规律

当气隙位置ρ的变化范围为11～16 mm时,高度差匹配规律、匹配后负刚度磁弹簧的负刚度幅值和非线性度分别如图4、图5、图6所示。从图4可知，在不同气隙宽度下，并随着气隙位置改变，匹配曲线变化趋势相同，但随着气隙位置增加，匹配曲线同时也表现出向右上方偏移；当气隙位置增大到15 mm时，匹配曲线不再发生偏移；进一步增大气隙位置，匹配曲线出现重叠，气隙宽度对匹配规律基本没有影响。

图5中，在不同气隙宽度下，随着气隙位置增大，负刚度幅值整体增大；在图5(a)中，当气隙宽度为4 mm，随着气隙位置增大到16 mm，负刚度幅值增大为-28～-26 kN/m之间；而在图5(d)中，当气隙宽度为10 mm，随着气隙位置减小为11 mm，负刚度幅值最小为-1.5～-1 kN/m之间；另外随着气隙位置增加，负刚度幅值曲线峰值增大。因此，对于负刚度磁弹簧的负刚度幅值的设计，可以通过增大气隙位置获得更大负刚度幅值，同时改变气隙位置也能够细化负刚度幅值取值区间，显然这就更适用于与正刚度弹簧匹配。

进一步分析不同气隙位置下非线性度的变化规律。具体结果如图6所示，在图6(a)中，随着气隙位置增加，非线性度从5.4%减小到2.7%；而在图6(c)中，随着气隙位置增加，非线性度从1%减小到0.6%；同时，随着气隙位置增加，非线性度的峰值改变并不明显。因此，在考虑到速度传感器对于线性负刚度的要求，显然更大的气隙位置更容易满足线性负刚度的要求。

为了满足速度传感器的低频扩展，负刚度特性在工作点附近应满足：与正刚度弹簧匹配的负刚度幅值，以保证系统低固有频率；保持尽可能小的非线性度，从而获得线性负刚度特性。基于以上分析，因此在负刚度磁弹簧设计中，可通过增大气隙宽度降低非线性度。虽然增大气隙宽度会导致负刚度幅值偏小，但可以进一步通过增大气隙位置来获得更大负刚度幅值并更小非线性度，从而获得速度传感器的低频扩展所需的线性负刚度特性。

4 传感器几何参数设计与性能分析

4.1 传感器几何参数设计

通过选配正刚度弹簧为DIN 2098圆筒形压缩螺旋弹簧，确定正刚度值为k=1 029 N/m，并结合3节的分析结果和速度传感器对于负刚度线性特性和线性范围的要求，确定传感器的几何参数设计流程如下： 首先根据传感器结构装配和线性负刚度的要求，确定负刚度磁弹簧最小内磁环内半径为5 mm、最大外磁环外半径为35 mm、气隙宽度为10 mm，并选取气隙位置为14 mm、高度差φc=10.8 mm、φv=36.2 mm，保证了最大非线性度要小于1.5%，根据上述参数得到负刚度磁弹簧刚度曲线α。然后通过减小气隙位置到11 mm，进而调整负刚度幅值，并保持较小非线性度,得到负刚度磁弹簧刚度曲线β；最后通过适当地调整高度差φc为22 mm，进一步减小非线性度和精确地获得需要的负刚度幅值，并匹配得出φv=34 mm，得出负刚度磁弹簧刚度曲线γ。

根据上述流程对负刚度磁弹簧进行设计，设计结果如图7所示。由图7可知，通过曲线α、曲线β、曲线γ的设计流程之后，曲线γ满足了非线性度低、正负刚度值匹配良好、线性位移区间大的要求，适用于速度传感器所需的线性负刚度特性。

基于以上设计，确定的负刚度磁弹簧的几何参数如表2所示。

表2 负刚度磁弹簧的几何参数确定值

基于表2参数，图8为双环永磁体PM1、双环永磁体PM2和负刚度磁弹簧的负刚度曲线。PM1的非线性度为5.38%，刚度为-313.21 N/m；PM2的非线性度为3.56%，刚度为-709.61 N/m；由PM1和PM2匹配的负刚度磁弹簧的负刚度增大为-1 022.82 N/m，非线性度减小为0.85%。基于式(13)和式(14),负刚度磁弹簧的拟合磁力Fm和刚度Km为：

(17)

(18)

4.2 传感器性能分析

定义x0为被测物体的位移，x为系统质量块的位移，相对位移y=x-x0=za，其中G1表示基于负刚度磁弹簧的速度传感器，G2表示基于理想线性负刚度磁弹簧的速度传感器。结合式(18)，传感器G1系统的动力学方程如下：

(19)

式中：m为等效质量；c为等效阻尼；L为线圈电感；R为外部负载电阻的阻值；q为传感器系统电路中的电量；T为机电耦合系数。

T表达式为

T=2πrnB

(20)

式中：r为线圈外半径；n为线圈匝数；2πrn为线圈的总长度；B为永磁体磁感应强度。

传感器系统基本参数如表3所示。

表3 传感器系统基本参数

通过龙格库塔算法对传感器G1方程(19)进行求解，输入采用谐波激励，谐波激励速度为

(21)

式中：A为激励幅值；ω为激励角频率。

为了验证传感器G1系统是否存在非线性动力学响应，设定激励幅值为0.005、0.01、0.05 m/s，基于频率扫描法得出传感器G1在不同激励幅值下的频响曲线如图9所示，传感器G1有着良好的幅频响应，能够很好地还原低频振动信号，并在不同激励幅值下的频响曲线基本保持重合。

进一步验证负刚度磁弹簧的非线性特性对传感器性能无影响，建立基于理想线性负刚度磁弹簧的速度传感器G2数学模型，假设负刚度磁弹簧为线性负刚度，基于式(18)，磁力的公式可简化为

Fp=-1 022.82za

(22)

将式(22)代入式(19)，得到理想线性负刚度磁弹簧传感器G2动力学方程：

(23)

设定激励幅值为0.005 m/s，基于频率扫描法得出传感器G1和传感器G2的频响曲线，并将所得的频响曲线与等效线性传感器G3的频响曲线进行对比。如图10所示，传感器G1和传感器G2频响曲线非常接近，因此传感器G1可以被视为线性系统，从而验证了负刚度磁弹簧非线性的影响基本被消除；由图10还可以得知，传感器G3的固有频率为4.9 Hz，传感器G1的固有频率为1.35 Hz，相对于传感器G3降低了3.14 Hz。结果表明：负刚度磁弹簧降低了传感器G1的固有频率，从而拓展了传感器低频测量带宽。

为了验证传感器G1有足够的线性测量范围，通过不同激励幅值的速度信号，分析传感器G1的相对位移时域响应。设定激励幅值为0.001、0.01、0.04、0.06 m/s，频率为1.35 Hz的谐波激励速度信号，传感器G1的相对位移时域响应如图11所示。当激励幅值为0.06 m/s时，传感器G1的相对位移响应的幅值为5 mm，达到了负刚度磁弹簧线性位移区间极值。因此，基于负刚度磁弹簧结构的线性位移区间为±5 mm，分析得出传感器的时域测量上限为0.06 m/s，验证了负刚度磁弹簧结构能满足传感器线性测量范围。

5 结束语

本文提出了一种基于负刚度磁弹簧的超低频速度传感器。首先通过等效磁荷法建立了负刚度磁弹簧磁力与刚度的计算模型。然后分析了轴向高度差、气隙宽度、气隙位置等参数对负刚度磁弹簧的负刚度特性的影响规律，并基于传感器低频扩展对负刚度特性的要求确定了负刚度磁弹簧几何参数。在此基础上，最后通过仿真分析了传感器时域和频率响应。结果表明：本文提出的基于负刚度磁弹簧的速度传感器机构以及负刚度磁弹簧几何参数确定方法能有效实现速度传感器低频扩展；同时，在不同激励幅值下的负刚度磁弹簧未引起传感器的非线性动力学行为，在保证了传感器足够的线性测量范围同时满足线性负刚度要求；同时本文提出传感器的固有频率为1.35 Hz，相对于等效线性传感器，固有频率降低了3.76 Hz，实现了低频扩展。

在后续的研究中进一步设计实验方案，与现有速度传感器进行对比，验证本文提出基于负刚度磁弹簧的速度传感器的各方面性能。