基于RFMRA和改进PNGV模型的锂离子电池SOC估算
刘冬雷,范永存,王顺利,夏黎黎
(西南科技大学信息工程学院,四川 绵阳 621010)
锂离子电池在新能源领域的应用日益广泛,健康状态的监测也倍受重视[1-2]。荷电状态(SOC)估算作为动力锂离子电池的关键技术之一,成为研究热点[3],准确地估算SOC可充分发挥电池的性能[4-5]。文献[6]建立了一种可变参数的模型,将建模误差由17.76mV降低到8.68 mV。文献[7]采用降阶模型,得到比全阶模型更高的精度。等效电路模型因物理意义明确、数学表达式简单等优点,被广泛应用[8]。
本文作者针对锂离子电池内部特性的复杂性和工作特性,在改进的新一代汽车合作伙伴(PNGV)等效模型的基础上,采用基于渐消记忆的递推算法(RFMRA)辨识模型参数,提出改进型RFMRA-扩展卡尔曼滤波(EKF)联合算法,以精确地估算电池的SOC。
1 理论分析
1.1 等效电路模型
在锂离子电池SOC估算过程中,电池等效模型的构建占有重要的地位。SOC的准确估算在很大程度上依赖于等效模型反应电池动态特性的准确程度[9]。实验采用一种改进的PNGV模型,等效建立锂离子电池模型。该模型在PNGV模型的基础上,串联一个RC回路,用于表述锂离子电池的表面效应电阻和表面效应电容,以提高精度,如图1所示。
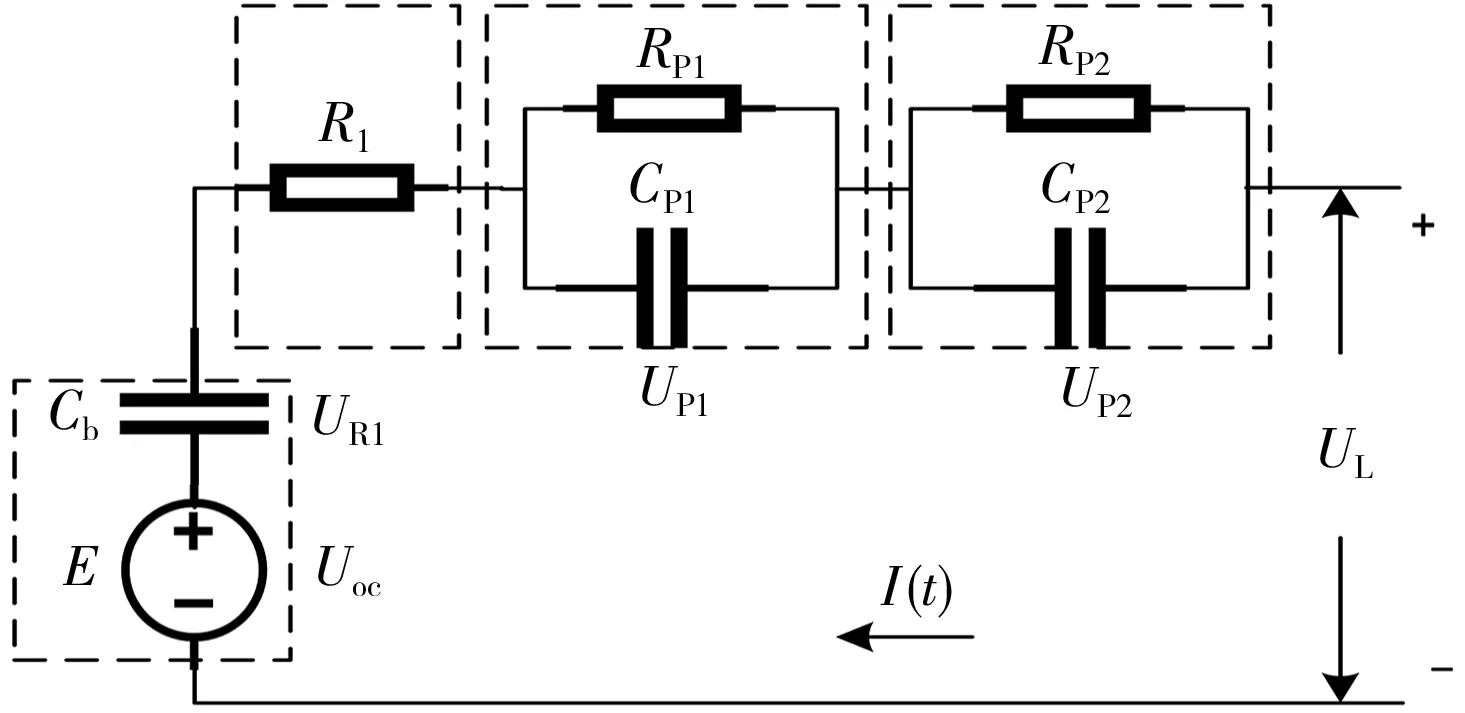
图1 改进的PNGV等效电路模型Fig.1 Improved partnership for a new generation of vehicles(PNGV)equivalent circuit model
图1中:Cb为电流的累积效应导致的开路电压的变化;Uoc为开路电压(OCV);E为未受到充放电影响时电池的电压;UL为端电压;R1为欧姆内阻;UR1为欧姆电压,是电池放电及结束放电瞬间的压降效果。代表电池极化效应的RC并联回路,由极化电阻RP1和极化电容CP1组成,其中UP1为极化电压;代表电池表面效应的RC并联回路,由表面极化电阻RP2和表面极化电容CP2组成,其中UP2为表面效应电压。
根据基尔霍夫定律,得到等效电路的电压和电流,如式(1)所示,Uoc是长时间静置后电池的稳定电压。
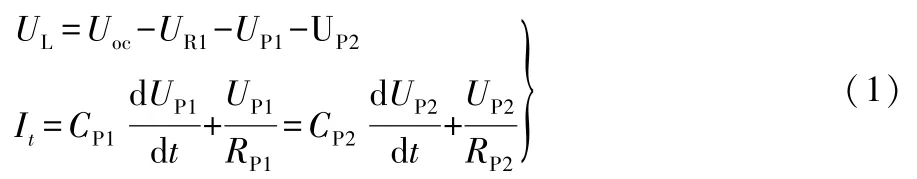
式(1)中:I为充放电电流;t为放电时间。
将参数 SOC(Soc)、UP1、UP2组成的参数矩阵[Soc,UP1,UP2]T作为状态变量,由式(1)获得锂离子电池的状态空间方程,如式(2)、(3)所示。
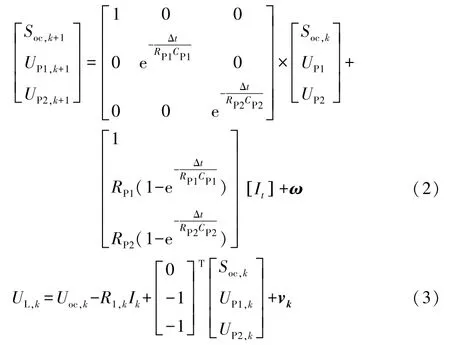
式(2)-(3)中:Δt为采样时间间隔;τ1=RP1CP1、τ2=RP2CP2;ω为状态误差,与建模误差有关;υ为测量误差,与传感器精度有关;e为自然常数;k为当前时刻;k+1为下一时刻。
1.2 RFMRA在线辨识
由于递推最小二乘法(RLS)存在“滤波饱和”现象,即随着迭代次数的增加,增益K和协方差M逐渐减小,算法对数据的修正能力逐渐变弱,最终导致参数辨识的误差越来越大。在RLS的基础上加入遗忘因子,可提高在线估算精度。遗忘因子的作用是在辨识过程中,对运行时间较长的数据给予较小的权重,对新的观测数据给予较大的权重。根据锂离子电池改进PNGV模型,可得到复频域方程[见式(4)]。

式(4)中:s为复频域算子。
采用双线性变换进行离散化处理式(4)中的传递函数,可以得到离散化的传递函数,如式(5)所示。
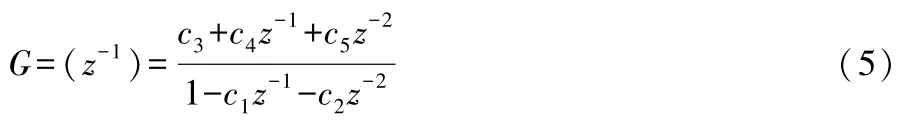
式(5)中:c1、c2、c3、c4和 c5为相应的常数系数;z为双线性变换算子。
从式(5)可知,所研究的系统是一个单输入单输出系统。将式(4)转换为差分方程,如式(6)所示。
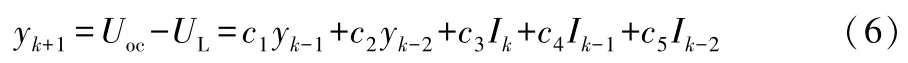
式(6)中:I为系统输入;y为系统输出;k-1为前一时刻;k-2为前两时刻。
可以推出锂离子电池参数与常数系数的关系,见式(7)。

式(7)中:T为取样周期。
将输入变量和参数变量用矩阵表达式来表示,如式(8)所示。

式(8)中:φk为k时刻的输入矩阵;θ为参数变量矩阵。
由式(8)得到系统输出的矩阵表达式,如式(9)所示。

引入遗传因子λ(0<λ<1),减弱旧数据的影响,增强新数据的反馈作用,RFMRA如式(10)所示。

1.3 EKF算法
EKF算法用于估计非线性系统,将非线性的状态空间模型进行线性化,再采用基本卡尔曼滤波(KF)算法实现估算。所用非线性离散系统的状态空间方程如式(11)所示。

式(11)中:Xk为状态变量;uk为系统输入;yk为观测变量;Ak为状态转移矩阵,可预测系统变量;Bk为系统控制输入矩阵;Ck、Dk分别为系统观测矩阵、驱动预测系统观测量。
EKF算法的递推过程见式(12)。

式(12)中:P为均方误差;G为卡尔曼增益;L为单位矩阵;Q和R分别是ω和υ的斜方差矩阵;h为转移矩阵;N为观测值。
2 模型在线参数辨识
以额定容量为70 Ah的三元铝壳单体锂离子电池(福建产)为实验对象,BTS200-100-104电池检测设备(深圳产)为实验平台,获取相关数据。
2.1 HPPC充放电实验
对锂离子电池进行混合动力脉冲能力特性(HPPC)测试[9],得到离线辨识结果,如表1所示。
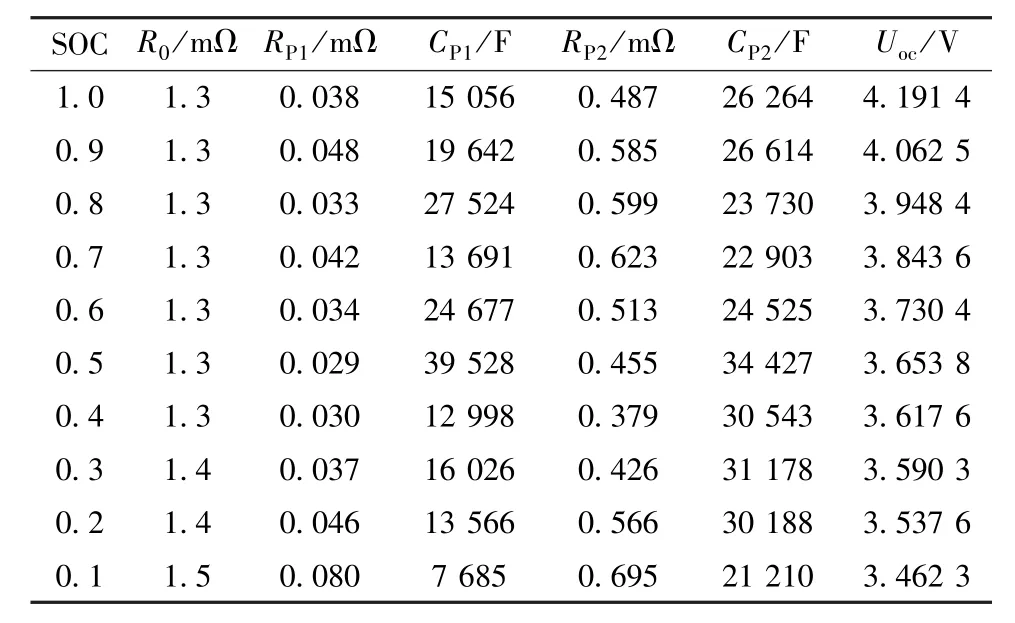
表1 不同SOC状态下的模型参数Table 1 Model parameters under different SOC states
由表1可得到OCV-SOC曲线,如图2所示。
从图2可知,电池在SOC为0.2~0.5时的非线性最强,通过多项式拟合,可得到Uoc与SOC的关系,见式(13)。
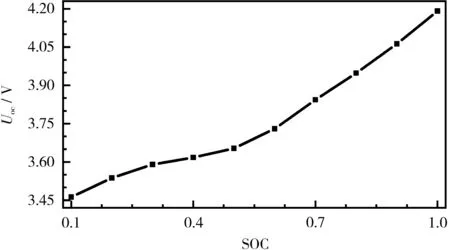
图2 OCV-SOC最小二乘拟合曲线Fig.2 OCV-SOC least square fitting curve
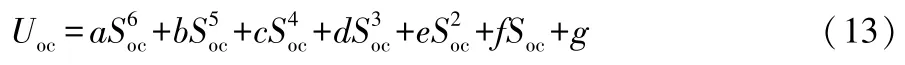
式(13)中:a、b、c、d、e、f和 g 均为拟合所得的各项系数。
2.2 在线参数辨识
采用RFMRA对所使用的改进PNGV模型的参数进行在线实时辨识,随着时间的推移,新的数据不断加入,使得辨识的参数能更准确地反映锂离子电池参数的实时状态。
在线辨识电阻和电容的结果如图3所示。
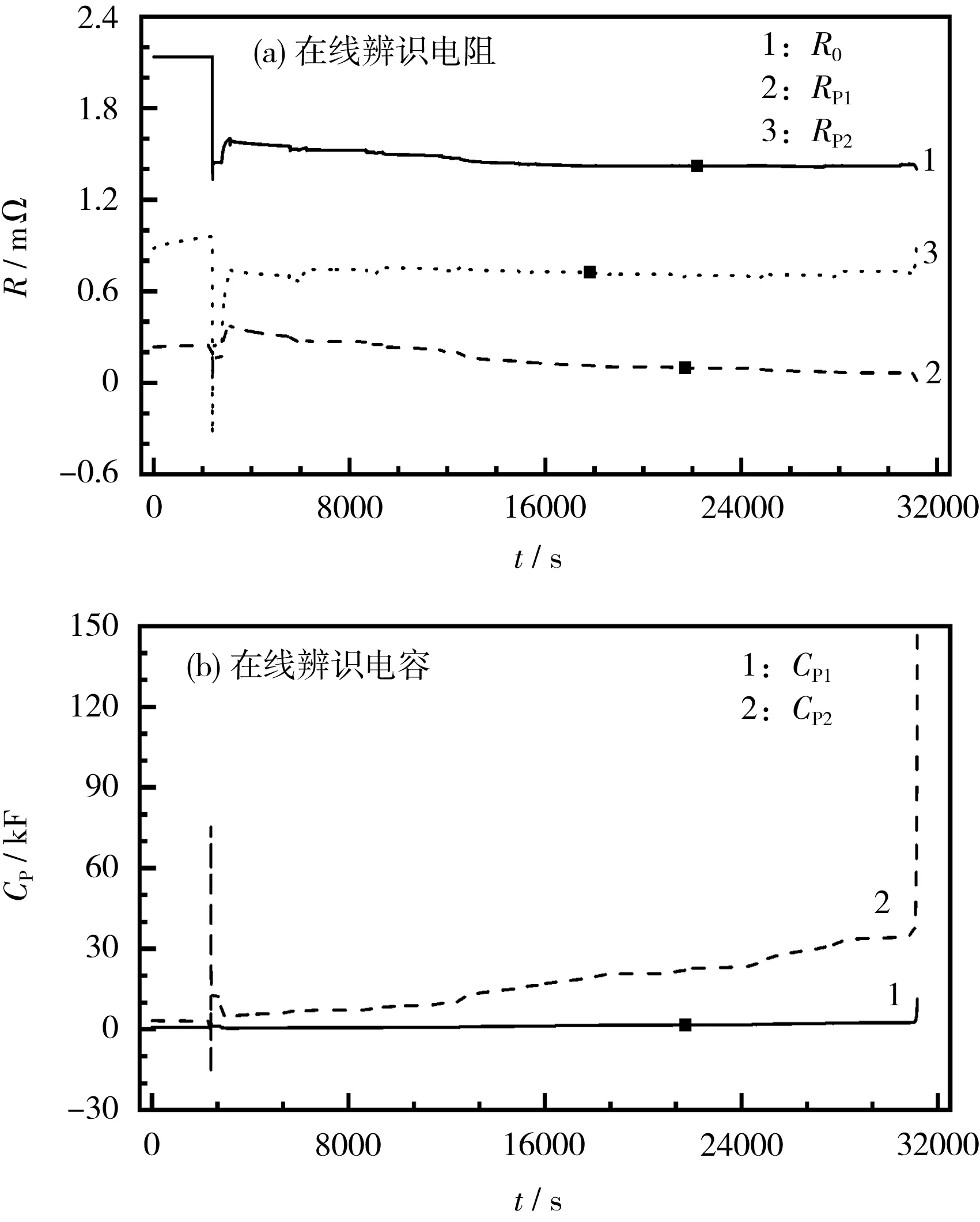
图3 改进的PNGV模型参数辨识结果Fig.3 Parameter identification results of improved PNGV model
在初始的辨识阶段,各个参数均有较大的突变,是初值与实际值之间存在的较大误差导致的,随着拟合数据的增多,各参数的变化趋于相对稳定。表面效应电容受电池内部化学反应的影响而逐渐增大。
3 实验结果分析
为验证在线算法对锂离子电池SOC估算的可行性,选用安时积分法得到SOC的标准值即真实值,误差取真实值与估算值的差值,对比分析离线参数辨识与改进型RFMRA-EKF联合算法在线参数辨识的SOC估算结果。
3.1 离线辨识实验结果
离线辨识估算SOC的结果见图4,初始SOC为1.0。
从图4可知,在起始阶段,SOC估算误差逐渐下降。当SOC>0.5时,最大误差为-3.092%,最小误差为-1.961%。此时,电池的线性性质相对较强,因此估算误差相对较小,离线辨识的参数还可满足估算精度的要求。当0.2 图4 离线EKF算法的SOC估算效果分析Fig.4 Analysis of SOC estimation effects of off-line EKF algorithm 在线辨识估算SOC的结果见图5,初始SOC设置为1.0。 图5 改进型RFMRA-EKF联合算法的SOC估算效果分析Fig.5 Effect analysis of on-line SOC estimation based on improved RFMRA-EKF joint algorithm 从图5可知,在起始阶段,SOC的估算误差呈下降的趋势,而且波动比离线算法要小。当SOC>0.5时,最大误差为-2.455%,最小误差为-0.277%。这表明所提出的改进型RFMRA-EKF联合算法可以在电池线性性质相对较强的区间获得更高的估算精度。当0.2 本文作者在改进传统的PNGV模型的基础上,提出一种改进型RFMRA-EKF联合算法,在线估算锂离子电池SOC。 与离线算法相比,所提出的联合算法最大误差降低了35.106%;总的估算结果中,MAE、MAPE和RMSE分别降低了7.21%、22.42%和25.38%。本文作者提出的锂离子电池SOC联合估算方法的精度满足实际需求,对实际的生产设计具有重要指导意义。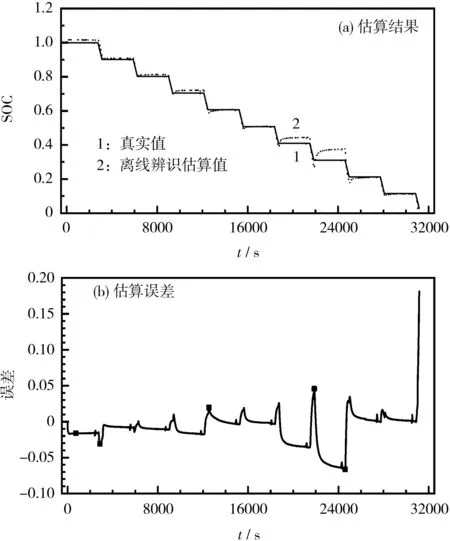
3.2 在线辨识实验结果

4 结论

